室内定位中基于EFIM和距离协作的节点选择算法*
马永涛,唐有朋,刘伟伟
(天津大学微电子学院,天津 300072)
随着无线传感技术的发展,无线传感器节点定位广泛应用在导航、监测、搜救等领域[1]。根据接收信号的不同特征参数,室内定位算法主要有基于信号到达时间TOA(Time-Of-Arrival)[2]、信号到达时间差TDOA(Time-Difference-Of-Arrival)[3]、信号到达角度AOA(Angle-Of-Arrival)[4-5]和接受信号强度RSS(Received Signal Strength)[6]。而无线传感器网络通常由位置信息已知的锚节点(Anchor)和位置信息未知的代理节点(Agent)构成。在二维场景中,确定目标节点的位置至少需要3个不同的锚节点。为了获得较高的定位精度,可以增大锚节点的功率或者增加锚节点的布置密度。但由于系统成本和实际环境的限制,室内协作定位的研究逐渐受到重视[7-8]。
协作定位可以避开锚节点大功率和高密度的要求,通过邻近节点的位置信息交换来确定目标节点的位置[9]。尽管节点协作可以提高定位性能,但信息的交换与融合也会造成计算复杂度的增加,减少辅助节点的数目可以节约系统成本,如电池能源、信道资源、计算资源等[10]。况且有些应用只需要达到适当的定位精度即可,例如在一个房间里达到米级的定位精度就足够了。在全球定位系统GPS(Global Positioning System)中早已应用了卫星选择,并且在这个领域里投入了大量的研究[11-13]。

在这篇论文里,介绍了几个常用的邻近节点选择算法,并提出基于EFIM和距离协作的节点选择算法。首先,介绍EFIM的概念并分析EFIM分别沿着不同的到达角度对位置估计的影响。接下来,详细地描述目标节点分别接收到锚节点和代理节点的位置信息后EFIM的更新变化。然后提出一种基于EFIM和距离协作的节点选择算法,根据该算法确定辅助节点的集合。最后,采用MATLAB仿真来验证该算法的性能。
1 系统模型
1.1 信号模型

(1)
式中:nkj表示观测噪声。假设节点i接收信号模型可写成:

(2)

(3)
式中:
(4)
且κi是第i个节点接收波形的多径参数向量:
(5)
κij是与zij(t)有关的多径参数向量:
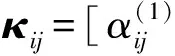
(6)
此外,还引进D作为观测向量:
(7)
式中:di=[di,1…di,i-1di,i+1…di,NA+NB]T和dij是通过zij(t)的K-L(Karhunen-Loeve)展开得到的[18]。
1.2 定位估计的误差界限

(8)
式中:JX是X的FIM:
(9)
式中:X由位置参量和信道参量两部分组成。简化后的FIM是一个2NA×2NA的对角矩阵,如果在二维场景中应用,则这个对角矩阵被称为EFIM。将其与式(8)联立,得到MSE:
(10)
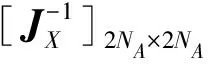
(11)
式中:Je(P)是P的EFIM。为了后面描述的方便,引进位置误差界限的平方SPEB(Squared Position Error Bound)的定义:
定义1(SPEB[20]) 在无线传感器网络中第i个节点的位置误差界限的平方SPEB定义为:
(pi)
(12)

(pi;q)
(13)
2 信息矩阵的分解与量化
2.1 分解FIM
为了分解费希尔信息矩阵FIM,需要知道联合分布f(D,X)=f(D|X)f(X),其中f(D|X)是一个似然函数,f(X)是参数X的先验分布。由于接收信号zij(t)是相互独立的,则f(D|X)可写成:
(14)
当多径参数κij是相互独立的,f(X)可以写成:
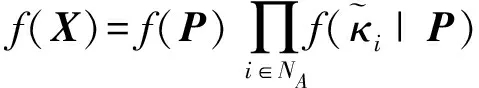
(15)
式中:f(P)是所有代理节点的联合概率密度分布,f(κij|P)是多径参数的联合概率分布函数。从式(14)可推出:
(16)
式中:第1部分表示来自锚节点的位置信息,第2部分表示代理节点的协作信息,最后一部分表示代理节点的先验位置信息。这时式(9)可写成:
(17)
假设代理节点的先验位置信息是未知的,则式(16)变成如下形式:
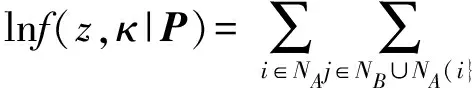
(18)
式中:κ表示信道参数向量,包含所有的κij,i∈NA且j∈NB∪NA{i}。
2.2 分解和量化EFIM
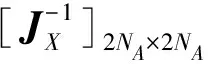
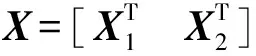
(19)
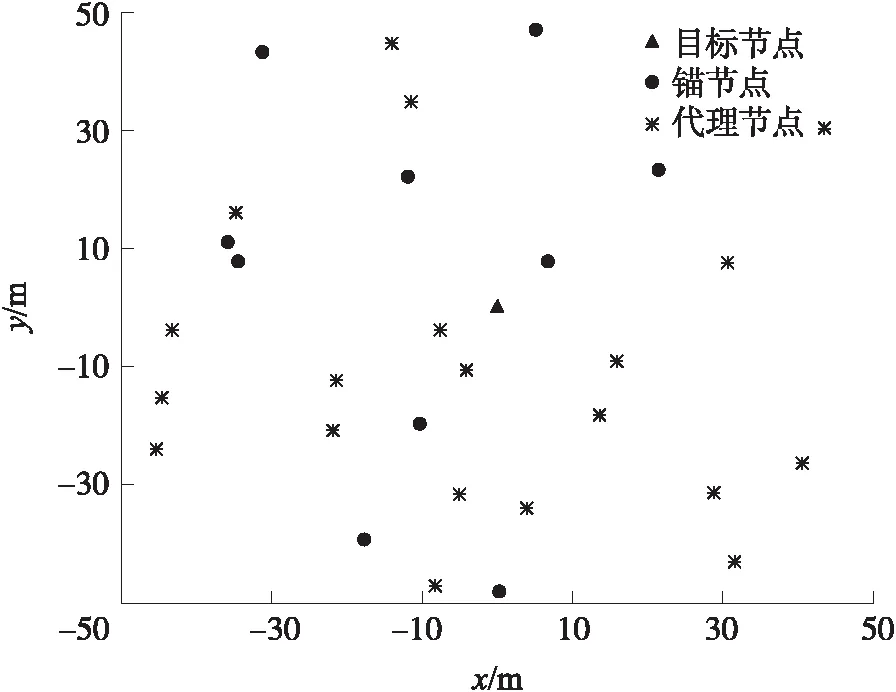
式中:X∈RN,X1∈Rn,A∈Rn×n,B∈Rn×(N-n),C∈R(N-n)×(N-n),且n Je(X1)A-BC-1BT (20) 为了进一步分解和描述EFIM,引进排列信息强度RII(Ranging Information Intensity)λij和排列方向矩阵RDM(Ranging Direction Matrix)Jr(φij)。假设节点的先验信息未知,则EFIM是一个2NA×2NA的矩阵,如式子(24)所示,则它可以被分解成如下两个部分: (21) Cij=Cji=(λij+λji)Jr(φij) (22) Jr(φ) (23) 它的两个特征值分别为0和1,非零特征值1对应的特征向量是q=[cosφsinφ]T,且Jr(φ)=qqT。所以相应的λJr(φ)是一个与角度φ有关的一维函数。 和式子(17)相比,EFIM在式子(24)中的结构与来自锚节点和代理节点的位置信息的结构相同。先验位置信息假设是未知的,在此不做讨论。 (24) 根据上述分析,做出如下的小结: 节点所携带的位置信息量越大则定位精度越高。每多增加一个节点参与协作定位,位置信息量就会增加,同时定位误差减少,且协作信息可以被分解成RII和RDM两个部分。 由于Je(P)是由RII和RMD组成,所以当节点间的相对位置固定时,则目标节点的定位精度由接收到的RII来确定。 节点的位置分布和信号传输的信道质量等许多因素都会影响定位精度。 协作定位的思想主要是节点间位置信息的共享,借助共享的位置信息实现定位。而大量的信息交换会造成计算复杂度的增加和能源消耗,此时,引进邻近节点的节点选择算法,选出最优的邻近节点最为辅助节点参与协作定位。不但可以获得较高的定位精度,还可以降低能源消耗。 由于协作信息来自锚节点或者代理节点,则辅助节点可能是目标节点周围的锚节点或代理节点,所以在这里分成两种形式进行讨论。用SPEB表示信息协作后的位置精度。 ①当目标节点和周围的锚节点协作时,则目标节点的EFIM可写成如下形式: (25) 式中:Iα是一个旋转角度α的旋转矩阵: (26) 式中:μ>η,且μ和η都是Je(pk)的特征值。在后面的写作中,用F(μ,η,α)代替Je(pi)。矩阵EFIM对角化后再与式(12)联立得: (27) 现在,分析锚节点对定位精度的影响。用F(ν,0,φ)表示来自锚节点的位置信息,其中ν表示RII。来自锚节点的位置信息是一维的,目标节点接收到信息的角度是φ。所以,当目标节点接收到来自锚节点的位置信息后,目标节点的EFIM更新为: (28) 式中: (29) (30) (31) 且φ′=φ-α。所以,SPEB更新为: (32) (33) (34) 式中: (35) (36) (37) 最近邻节点选择法首先计算目标节点与邻近节点的距离,然后按照距离大小进行排序,根据需要选择与目标节点距离最小的邻近节点作为辅助节点的集合。借助这些辅助节点进行定位比选择其他的节点集合参与协作的定位精度要高,说明定位精度与距离有关,且距离越小定位越准确。但在实际应用,并不是距离目标节点越近的邻近节点携带的位置信息量越大,邻近节点的位置信息或多或少,也是影响定位精度的重要因素。例如,某些邻近节点与目标节点间的距离都很近,但携带的位置信息量存在较大差异时,那么对定位精度起决定性作用的是信息量而不是距离。如果此时选择距离稍大且信息量也大的邻近节点,不但不会增加能源消耗反而会大幅度地提高定位精度。为了解决根据单个标准距离或信息量选择辅助节点的集合带来的问题,本文提出一种新的节点选择算法——基于EFIM和距离协作的节点选择算法,如算法1所示。该算法的节点选择标准是携带节点间距离d的SPEB(d): (38) 在算法1中,如果Λk≫Γk,说明邻近节点的数量太多,需要适当地减小节点的通信半径Rk。如果Λk=Γk,这时有两种情况,一种是使用了所有的邻近节点刚好满足定位精度的要求;另一种是使用了所有的邻近节点仍不能达到设定的定位精度,在这种情况下,需要适当地增大通信范围Rk,在这篇论文里不做讨论。在节点选择的过程中,如果遇到的邻近节点是锚节点,那么它比代理节点有更大的可能被选择进入辅助节点的集合参与协作定位;如果遇到的邻近节点是代理节点,则必须先计算ξkj(0<ξkj<1),再判断是否可以作为辅助节点参与协作定位。 算法1基于EFIM和距离协作的节点选择算法 图1 仿真场景图,目标节点周围覆盖着10个锚节点和20个代理节点 由于实验条件的限制,这里通过MATLAB进行200次蒙特卡洛仿真试验来验证本文提出的一种基于EFIM和距离协作的节点选择算法的性能,并与已有的节点选择算法进行对比。假设仿真是在一个100 m×100 m二维场景里进行(如图1所示),目标节点的坐标是(0,0),周围有10个锚节点和20个代理节点,它们有着不同的旋转角度α和不同的到达角度φ,且它们到目标节点的距离也各不相同。 (39) (40) 图2 不同的信号到达角度,有效RII和RIIν12的关系 图3 对于不同的方法,选择的节点数目与定位精度的关系 (41) 如图3所示,目标节点的定位精度随着辅助节点数目增加而提高。NNSM和其他算法相比其定位精度是最低的。基于EFIM的节点选择算法,忽略了距离对定位精度造成的影响,因此定位精度不如新提出的算法。克拉美罗下界法是选择位置估计协方差最小的邻近节点作为辅助节点,借助这些节点定位会获得较高的位置估计精度,但忽略了定位误差的方向。新提出的算法是基于EFIM和距离的协作,从图3可以看出定位精度明显提高。 图4反映的是设定的SPEB和辅助节点数目的关系。SPEB值越小,定位精度越高,定位所需的辅助节点越多。例如,设定SPEB门限g0=0.8,新提出的算法只需要2个节点就能满足要求,从图3上可以看到这时的定位精度是1.07 m;而CRLB法则需要3个节点,此时的定位精度是1.06 m;EFIM法和NNSM则分别需要4个和5个节点,它们的定位精度分别是1.03 m和1.04 m。当设定某一个SPEB门限值时,上述4个方法实现的定位精度相差很小,但新提出的算法所需要的节点数目是最少的。如果选择6个邻近节点作为辅助节点参与协作定位,则新提出的算法得到的定位精度是最高的0.79 m,而CRLB法得到的定位精度次之是0.87 m,EFIM法和NNSM得到的定位精度分别是0.92 m和0.93 m。因此,可以证明本文新提出的算法定位性能更好。 图4 对于不同的方法,设定的SPEB门限值和选择的节点的数量之间的关系 图5 定位精度和系统消耗的能量之间的关系 上述的仿真过程,考虑能量消耗和信号路径损耗。参与协作的辅助节点越多能量消耗越大;目标节点和邻近节点的距离越大,信号传输的路径就越长,信号损耗和能量消耗就越大。从图5可以看出,定位精度和能量消耗之间的关系。新提出的算法与其他方法相比,能量消耗更少。 为了解决协作定位带来的问题,在协作定位网络中对邻近节点进行节点选择以实现较低的能量消耗、较高的定位精度。首先获取邻近节点到目标节点的距离,然后通过推导更新EFIM来计算SPEB,并分析邻近节点的EFIM沿不同角度对目标节点位置估计的影响。然后提出一种基于EFIM和距离协作的节点选择算法,借助辅助节点对目标节点进行定位。仿真结果表明,新提出的算法和其他几种算法相比,当选择相同数目的节点时定位精度提高,或者达到设定的定位精度时选择的节点数目最少。应用新提出的算法,定位系统能量的消耗降低,进而提高了能量利用率。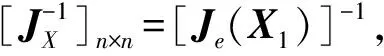
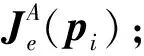

3 节点选择算法
3.1 计算SPEB
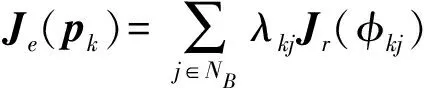
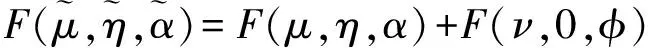

3.2 基于EFIM和距离协作的节点选择算法

4 仿真结果分析





5 结束语

