看学生的解题报告，探促进学生积极思维的若干策略

安徽省安庆一中 (246000) 陈贤清

以发展学生的智力、培养能力和创新精神为出发点的数学教学，强调学生独立自主的探究和发现.通过问题解决、探究性学习等，可以使学生体验探索新知的方法，使他们的创造力得到培养，这种开放型的课堂，学生的自由度高，面对的困难也多，这就需要学生积极思维，积极地去面对困难、战胜困难.当前，问题解决的模式与步骤、探究性学习的模式与方法等常见于各种刊物，我们在欣喜地看到这一切的同时，应该进一步关注学生积极思维习惯的培养.

积极思维的习惯比一切思维方法还重要.诺贝尔物理奖获得者温贝格曾说：现在最好的学生与次好的学生的区别，不在于知识的多少，而在于有无对未知领域的进攻精神.没有积极思维的习惯，就不会积极地去进行问题解决、积极地对未知进行探究，空有一身解决问题的方法也不能运用；有了积极的思维习惯，才会敢想敢干，就能逢山修路，遇水架桥，没有方法就去积极地创造方法，有了方法还会不断的对方法进行改进和提高.

下面通过学生的三个解题片断，展示学生积极思维的神奇之处.

案例一：设疑置趣，创设积极思维的氛围

在学生的最近发展区设置问题、在无疑处生疑，从学生现实生活中引入、活动引入、数学史引入等都可以激发学生积极思维.同时，课堂便是情感场.教师的一言一行、一举一动无不影响着学生的情绪.教师要以自己的激情点燃学生的激情，以自己的积极思维引导学生的积极思维.

例1 线性规划第一课时的教学

我的预案是：通过学生探究，发现需要定义“点在直线上方”，再推出它等价于：y0>y′⟺y0>

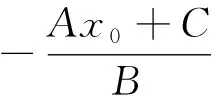
师：点P(x0,y0)在直线L：Ax+By+C=0上，则有Ax0+By0+C=0，点P不在直线L上，会有什么情况呢？

大家异口同声地答道：Ax0+By0+C≠0是Ax0+By0+C>0，还是Ax0+By0+C<0呢？

同学们议论纷纷，通过取值试验，发现都有可能．接着问：什么时候Ax0+By0+C>0，什么时候Ax0+By0+C<0？

探索的欲望被激发，同学们跃跃欲试，有的画图，有的取特殊值运算．

片刻后有同学回答了：若点P坐标满足y0>kx0+b，则P点在直线上方区域，若y0

师：(与预案不同，先让学生说)你是怎样发现这个结论的？

生：我取了三组特殊值验证，结论都成立.因此，我认为应该有上述结论.

师：三组？哪三组？

生：y>2x+3,y>-2x+3,y<2x+3.

师：面对未知，取特殊值进行探究的思路是可取的.它具有一般性吗？

生：我想起来了，还应该再验证五个式子：

y<-2x+3,y>2x-3,y>-2x-3,y<2x-3,y<-2x-3,

师：为什么要取这八组值呢？

生：这里共有三个变量：分y>…,y<…,k>0,k<0,b>0,b<0一共只有八种情形.

师：想得真全面!(同学们也不禁为他的灵机应变和缜密的思维鼓掌)大家取特殊点验证看看是不是有上述结论成立？

生：真成立耶!我用的是直线方程的一般式，为什么找不到规律昵？我取点P(3,2)，适合x+2y-3>0(1),x-2y+3>0(2)但画图却发现点P在(1)的上方，(2)的下方，这又是为什么呢？(天赐良机，可以引导学生发现需要给出定义！)

有不少同学附和着，我也这样做的，还以为没规律呢!

师：什么叫点P在L上方呢？我们怎样用“量”来刻划它？

一堂成功的课，离不开良好的探究情境和学习氛围.探究情境需要靠教师智慧地去创设，学习氛围需要靠师生互动来营造.对学生的异想天开，我们要宽容，并鼓励他们自己去证明.让学生体验发现的乐趣、经历进步的过程、享受成功的喜悦.“我们往往把学生想象成什么样子，就真的会成为什么样子.”对学生不成熟甚至错误的想法，我们要积极寻找其中的合理成份与积极因素，在尊重原创的基础上鼓励学生自己去补充完善.课堂上老师的微笑是一种比“好”、“对不起”之类的口语更微妙的无声语言，能起到无声胜有声的作用.对学生的关怀不是口号，而是体现在这些细节中，良言一句三春暖.这种民主、平等、宽松的环境，几节课下来，课堂上不肯思考、不愿回答、想当然回答问题的同学少了，积极思维的同学多了.

案例二：直面困难，提供积极思维的时机

有效的解题教学，尤其是综合题教学，首先要培养学生面对困难的勇气，特别是平时教学中要提供给学生直面困难的机会.要鼓励他们“只要有一线希望，就要尽百倍的努力.”只有敢于面对，才能积累战胜困难的勇气与信心.其次才是培养他们解决问题的策略，遇到困难时可以按步骤问自己一些问题：题意理解是正确的吗？现在的问题是什么？可还有什么隐含条件没发现？能画一个简图吗？……

在一次例题教学中，我举了这样一个例子：

也有同学说：从图形中也可看出k=1一定是方程(3)的一个解，将方程(3)左边除以因式k-1，就得到(4)，从而解出答案.

人在紧张的时候有两种截然不同的反应，一是心虚胆怯、畏缩不前、思路闭塞；一是“急中生智”，正常发挥甚至超常发挥.例题教学中如何避免前者实现后者，关键在于选题.题目难度要适当，大多数人跳一跳能够得着；题目的结构要精巧，能对学生产生良好的心理刺激.这样，学生每节课都在期待着新鲜、精巧的题目出现，并以巨大的热情投入智慧含量较高的活动中.同时教师必须营造出既紧张严峻，又宽松和谐的课堂氛围，使学生在未曾动手之前就具有征服题目的心理优势，于是智慧闸门洞开，信心和兴趣陡增，求胜欲、竞争欲、表现欲骤升，学生的潜能得到挖掘，“急中生智”成为可能.在突破取得成功之后，学生还会形成克题制胜的良好情绪记忆，对未来的“战斗”产生积极与持久的影响.

案例三：暴露思维过程也暴露心理历程，促进积极思维品质发展

(Ⅰ)若b=2，且h(x)=f(x)-g(x)存在单调递减区间，求a的取值范围；

(Ⅱ)设函数f(x)的图像C1与函数g(x)图像C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，证明C1在点M处的切线与C2在点N处的切线不平行.

这是我在一次考试中用过的题目.据事后统计：全班50人有46人做了第一问，其中40人做对；第二问只有4人做对.试卷评讲时，我就让做对的同学谈谈他在考场上是如何想的(而不仅仅讲如何做的).

前面都很顺利，到这里我当时做不下去了，真想放弃算了.想到平时老师您教我们的方法，再看了一遍题目，题意理解是正确的，就是在上述三个式子中找出矛盾.

很多同学附和着说，我也这样想的呀，就是找不出矛盾，这三个式子不知如何处理.(我用举手的方法调查了一下，有38人想到了这一步)

知道思路是对的后，我相信我一定能做出来，人马上就冷静下来了.再看三个式子，(2)(3)两式不和解析几何里“设而不求”时的情况很类似吗？在那里都是把两式相减，我也这样一试，果然成功了!

师：真是试一试就行，争一争就赢啊!

接着，还有同学在此基础上提出新的做法(略).

师：在这些方法中，解决这道题的关键是什么？

生：发现(3)式-(2)式!

生：遇到困难要积极动脑，要试一试，不要轻易放弃!

生：积极思维真神奇啊!

近来我们一直强调“暴露思维”式的教学，但只暴露思维是不够的.还要抓好对暴露出来的思维的剖析，找出其中的智力价值，帮助学生找出发现问题的“拐点” (很多难题其实就是那一个拐点我们没拐过去)，告诉他突破拐点的方法.教师不仅要暴露思维，还要展现自己解题中的情感历程.数学问题的条件与结论、归纳与联想、结构与模式、逻辑与直觉之间的联结并非一帆风顺，其间存在着模式的识别、方法的抉择及困难的解脱等各种矛盾，掺杂着解题者的心理活动.教师表露解题时的心情，会使学生随着解题的推进，感受到解题智慧的萌动、联翩念头的浮想、战胜困难的坚韧等.体验理智与情感交织的韵律，获得解题外的感受.G波利亚在《怎样解题》中，字里行间不也时时流露出“如果你有一个念头，你是够幸运的了”、“好的题目和蘑菇有点相似，它们都成串生产”等亲切话语吗？当教师用言语表达自己的解题情感时，将使学生不觉间置身其中，难以言传的感受油然而生.

要培养学生的自主探究、勇于创新的能力，积极思维的习惯，教师自己首先要勤于探究、积极思维、不断创新.不断学习、敢于创新不仅是教育者的一种精神，一种境界，也是一种教育状态和理想信念．学生可以潜移默化、润物细无声地从教师身上感悟到，并慢慢地将它变成自己的一种追求、一种精神、一个境界．让我们用积极思维成就学生的辉煌人生吧.