基于模型参考模糊自适应的转台摩擦力矩补偿研究

姜云翔 王春喜马 玲 曹雪立 王 茂 赵 健

(1.北京航天计量测试技术研究所，北京 100076；2.哈尔滨工业大学，哈尔滨 150001；3.北京航天控制仪器研究所，北京 100039)

1 引 言

伺服转台是一类广泛应用于航天、航空等领域的精密设备，随着航天航空技术的高速发展，伺服转台的控制性能也需要不断提高。摩擦干扰力矩的存在严重制约着伺服转台的控制精度，特别是对于高精度低速伺服转台，其摩擦干扰尤其突出。因此必须设计相应的摩擦补偿方法对摩擦力矩进行补偿。本文以某型双轴伺服转台研制为背景，对其控制系统的设计及摩擦补偿技术展开研究，以实现该转台承载的光学相机对空间飞行器的快速高精度跟踪。对抑制摩擦干扰进而提高伺服转台的动态跟踪精度具有一定的理论意义和实用价值。

2 系统模型建立

目前，在工程中经常采用的摩擦模型有库仑模型、库仑摩擦+粘滞摩擦模型、静摩擦+库仑摩擦+粘滞摩擦模型、Stribeck 摩擦模型、LuGre动态摩擦模型[1]。综合考虑工程实现难易和对摩擦现象描述的准确性，本文选用可以较为准确地反映摩擦力特性的 Stribeck 摩擦模型。该模型可表示为

(1)

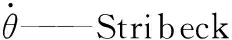
表1 Stribeck模型参数估计

对于直流力矩电机，忽略电枢电感及阻尼系数的影响，建立如图1所示的数学模型框图。

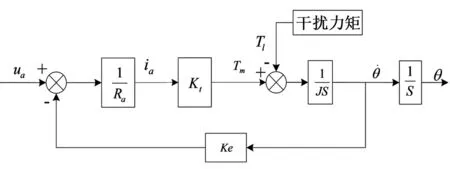
图1 被控对象数学模型框图Fig.1 Block diagram of the mathematical model of the controlled object

对应上图，可以得到实际被控对象的数学模型如式(2)所示。

(2)

不考虑摩擦力矩作用时的系统模型作为标称模型如式(3)所示。

(3)

系统参数确定如表2所示。

表2 系统参数

3 模型参考模糊自适应

模型参考模糊自适应控制是利用模糊控制器代替常规的、复杂的自适应控制器[2]，该方法并不要求对参考模型和实际被控系统建立精确地数学模型，而只要根据系统的模糊信息，用模糊条件语句写出控制规则，鲁棒性好，实时性好。其控制原理图如图2所示。

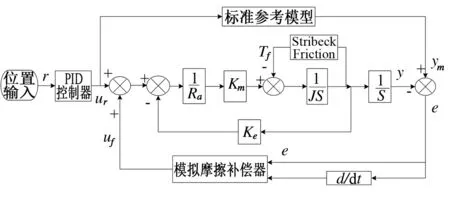
图2 MRFAC摩擦补偿控制原理图Fig.2 MRFAC principle diagram of friction compensation control

模糊控制器的设计是MRFAC中的核心环节，其需要根据不同的控制对象特征调整模糊控制规则。下面对模糊控制器进行分析设计。模糊控制器的基本结构如图3所示。

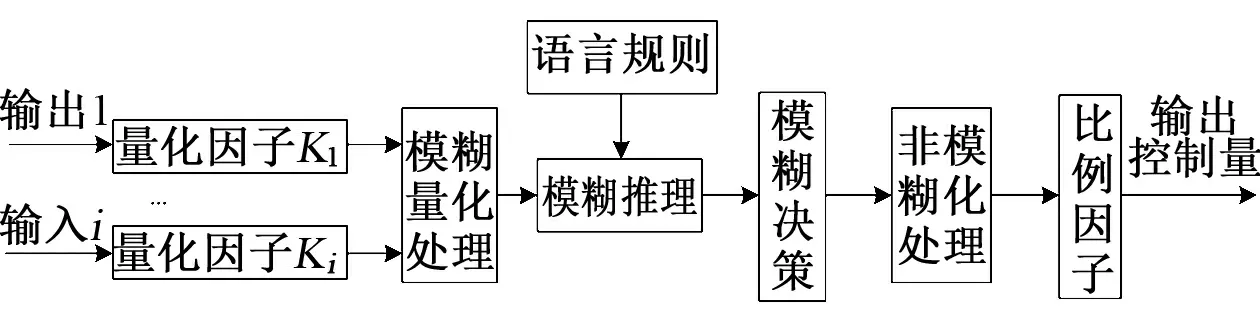
图3 模糊控制器的基本构成图Fig.3 Basic composition diagram of fuzzy controller

目前人们广泛设计和应用二维模糊控制器。设计步骤如下:

(1)确定模糊控制器的输入、输出变量

在本摩擦补偿控制中，选择工程中常用的二维模糊控制器，以E、Ec作为模糊推理的输入，以uf作为摩擦的补偿直接作用于实际被控对象。

其中：E——实际系统模型与标准模型的位置误差；Ec——实际系统模型与标准模型的位置误差变化率；uf——模糊控制的输出。

(2)选择描述模糊控制器输入和输出变量的词集

在本系统中，通过查阅文献及经验，选择七个词汇描述输入、输出变量。即位置误差E，误差变化率Ec和模糊推理的输出uf的模糊词集均取为：{负大、负中、负小、零、正小、正中、正大}，一般用英文字头缩写为{NB，NM，NS，ZO，PS，PM，PB}；在这里取位置误差E，误差变化率Ec，模糊推理的输uf的论域均为{-3，-2，-1，0，1，2，3}。

(3)隶属度函数

隶属度函数对模糊控制器的控制效果至关重要，在此，模糊控制器的输入以及输出变量均选取S型，三角形、Z型交叠对称分布的隶属度函数。曲线如图4所示。

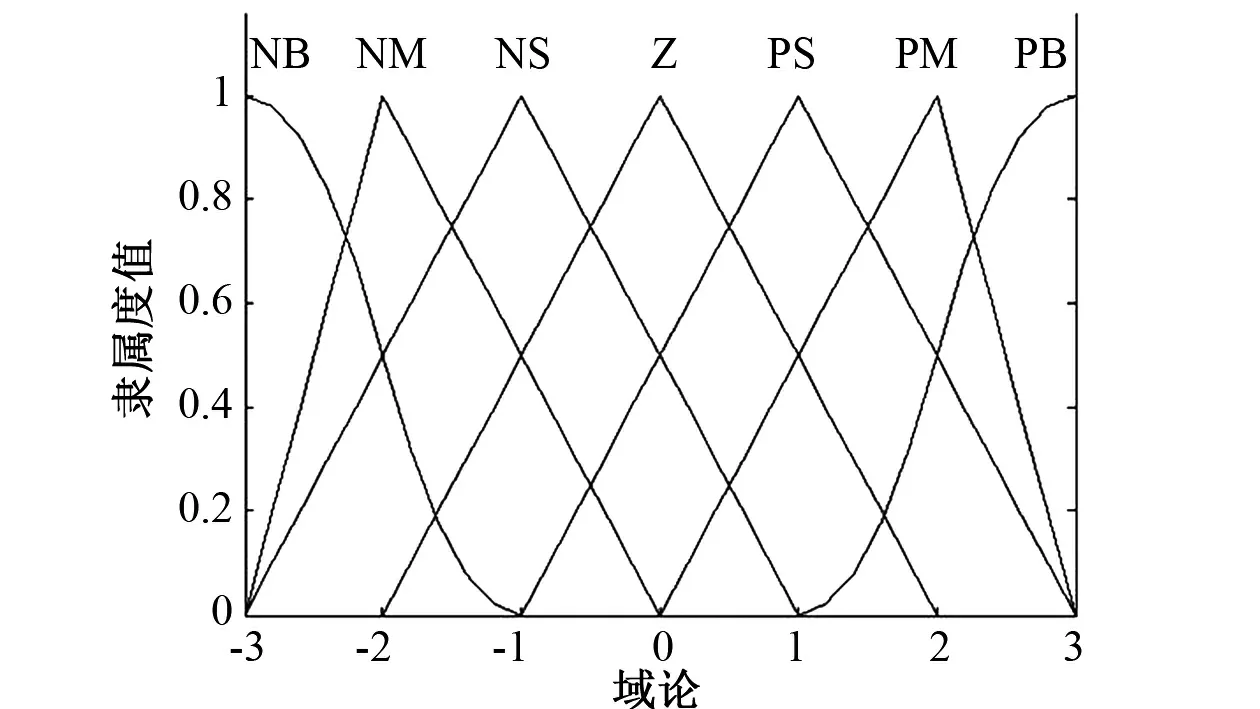
图4 隶属度函数曲线Fig.4 Membership function curve

(4)模糊控制规则

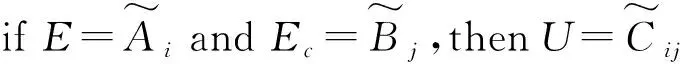
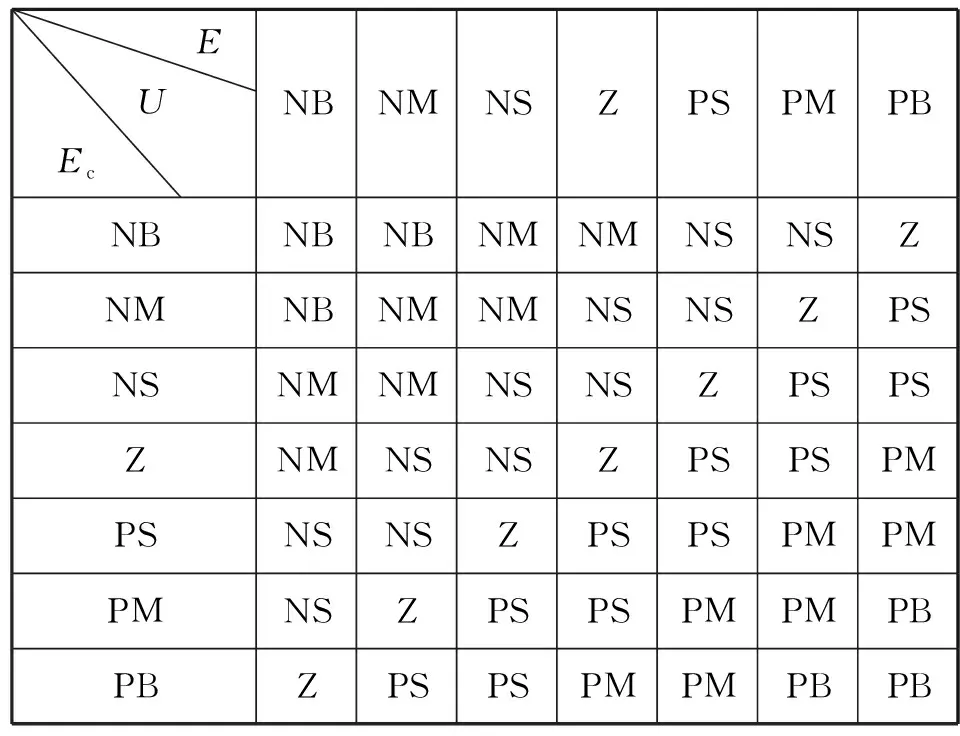
表3 模糊控制规则表

(5)非模糊化方法

通过上述模糊控制规则经过模糊推理得出的控制变量是一个模糊子集，它是一个模糊量而不能直接控制被控对象，还需采用合理的方法将模糊量转化为精确量，以便最好地发挥模糊推理决策的效果，在本文中，采用面积中心法(centroid)。

(6)量化因子和比例因子的选择

量化因子和比例因子可以将模糊控制器的输入变量及模糊控制器的输出量映射为实际被控系统的输出误差和误差变化量以及其对应的输入控制量。表示为式(4)。

Ke=n/Xe
Kc=m/Xc
Ku=Yn/l

(4)

式中:Ke——误差对应的量化因子;Kc——误差变化对应的量化因子;Ku——控制量对应的比例因子;Xe,Xc——分别为误差和输入变量的基本论域最大值;Yn——输出变量的基本论域最大值;n,m,l——分别为模糊子集。

许多研究者经过实验证明，在模糊控制器的控制规则及隶属函数确定的情况下，其量化因子、比例因子的大小以及量化因子之间的相对大小关系，对模糊控制器的控制性能影响极大。因此，在模糊控制器的调试环节，主要是通过对量化因子和比例因子进行调整，确定一组合理的值，从而使系统获得较好的响应效果。

4 模型参考模糊自适应控制器的稳定性分析

一个控制器的设计首先要保证的是稳定问题，目前常用于分析模糊控制器稳定性的方法有以下几种：描述函数法、线性近似法、相平面法等[3]。本文选用线性近似法对系统模糊控制器的稳定性进行分析。

将实际被控系统的动态方程，即式(2)表示成如下的状态方程

(5)

式中:Ap,Bp,Cp——分别为闭环控制系统的状态转移阵、控制矩阵以及输出矩阵。

参考模型的状态方程表示如下

(6)

式中:Am,Bm,Cm——分别为参考模型闭环系统的状态转移矩阵、控制矩阵以及输出矩阵。u,uf的定义同式(3)中。

式(5)中，模糊控制器和摩擦力矩干扰均为非线性系统，下面分别将其进行近似线性化表示，从而对MRFAC系统进行稳定性分析。

4.1 摩擦模型的线性化

如式(1)所示，Stribeck摩擦模型具有显著的非线性，对stribeck摩擦函数进行求导得到式(7)，由此确定Stribeck摩擦曲线的走向，这样能确定更准确的分段线性函数[4,7]。

(7)

(8)

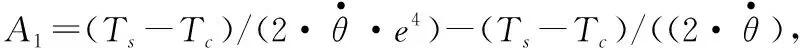
利用Matlab对Stribeck摩擦曲线进行绘制，即式(7)及分段线性函数式(8)描述的曲线，如图5所示。

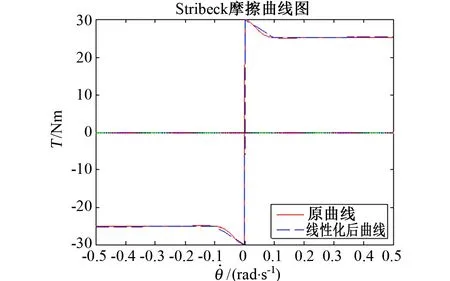
图5 Stribeck摩擦曲线及其线性化曲线Fig.5 Stribeck friction curve and its linearization curve

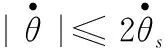
4.2 Lyapunov稳定性证明

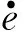
(9)

式中：

(10)

将式(9),式(10)代入式(5)，可得下式

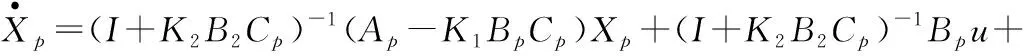
(11)

记Φ=(I+K2B2Cp)-1(Ap-K1BpCp),X0=(I+K2B2Cp)-1Bpu

则式(11)，即被控对象的状态方程可表示为

(12)

选择的参考模型是稳定的，则当t→时，有因此，当t→时，(I+K2B2Cp)-1

ΦTP+PΦ=-Q

(13)

式中:P,Q——正定实对称矩阵。由式(13)可以推理保证系统稳定的K1和K2的范围，用式(14)的不等式表示

α1≤K1≤α2,β1≤K2≤β2

(14)

因此，满足稳定的模糊控制器输出u可以表示为如下的不等式

(15)

当模糊控制器输出满足式(15)时，则能证明该控制系统稳定。

由式(15)可以看出，模糊控制器输出在一定范围内变化，正是由于这种输出的动态调整作用，才使得模型参考模糊自适应系统具有较强的自适应能力，从而对复杂控制模型具有较好的控制效果。

5 实验结果分析

为了验证上述摩擦补偿方法的效果,本文进行了数值仿真。选取参考输入的位置信号为

θd=Asin(2πft)

(16)

式中:A——位置信号的幅值，取A=2；f——位置信号的变化频率，取f=0.16Hz；t——时间。

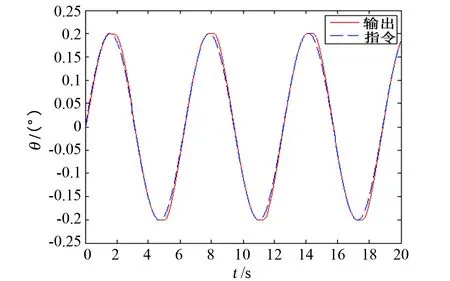
图6 未补偿位置跟踪曲线Fig.6 Uncompensated position tracking curve

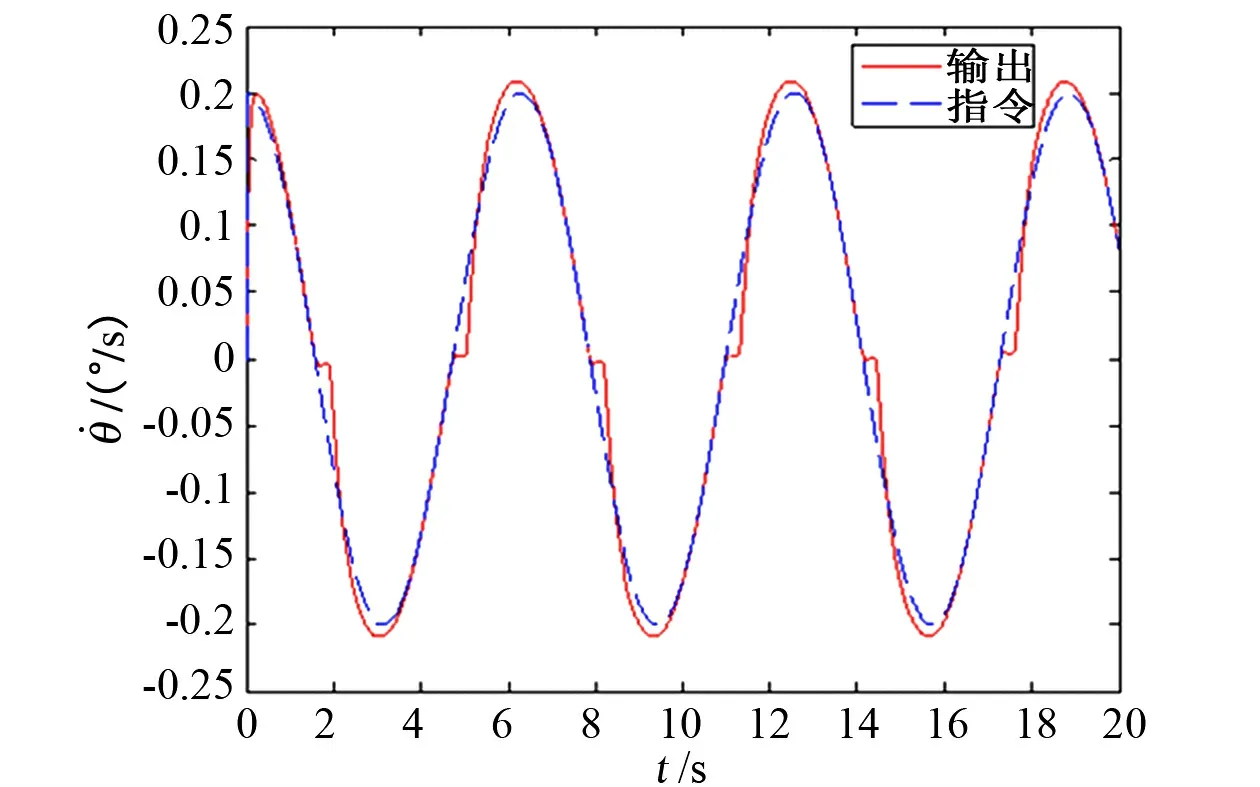
图7 未补偿速率跟踪曲线 Fig.7 Uncompensated velocity tracking curve

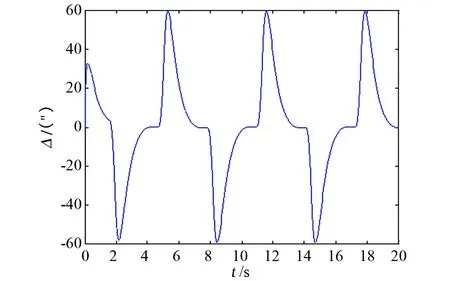
图8 未补偿位置跟踪误差曲线Fig.8 Uncompensated position tracking error curve

从未进行摩擦补偿的曲线可以看出，受摩擦力矩的影响，位置跟踪曲线有明显的“平顶”现象，速率跟踪曲线有死区现象，位置跟踪偏差大；而从进行摩擦补偿的曲线可以看出，其位置跟踪曲线的“平顶”现象及速率跟踪的“死区”现象均有明显改善，且位置跟踪偏差显著下降至10″以内，提高了转台的伺服精度。

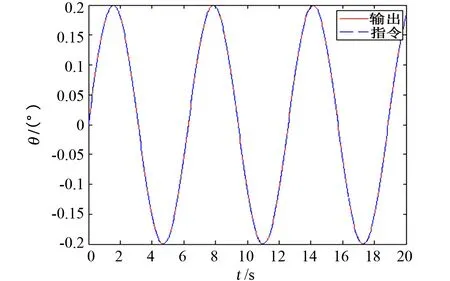
图9 补偿后位置跟踪曲线Fig.9 Position tracking error curve after compensated

图10 补偿后速率跟踪曲线Fig.10 Velocity tracking curve after compensated

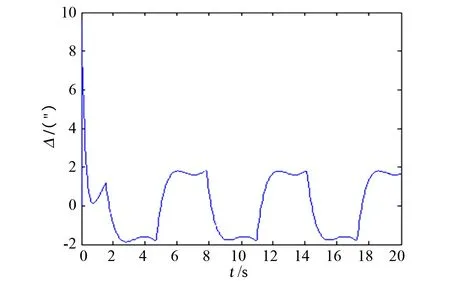
图11 补偿后位置跟踪误差曲线Fig.11 Velocity tracking error curve after compensated

6 结束语

针对某型伺服转台在摩擦力矩干扰下引起的低速爬行问题，本文设计了基于模型参考模糊自适应方法的摩擦力矩补偿控制方案，并进行了稳定性分析以及仿真论证。仿真结果表明，该摩擦补偿方法能够有效抑制摩擦干扰的不利影响，显著提高了转台的伺服精度。