核心素养下的小学数学“概率”课教学模式探索与思考

郑龙

中图分类号：G623.5 文献标识码：B 文章编号：1672-1578（2018）24-0152-02

2011版《新课程标准》把数学内容分为四大领域，其中一个重要领域就是“统计与概率”。“统计与概率”在生活中的应用是广泛而有意义的，大至一个国家，小至一个企业或者个人，社会的方方面面也都离不开统计与概率。在我们生活的世界中存在着大量的无法确定的随机现象，认识它们可以帮助学生科学的认识世界，做出决策，可以说现实生活已经先于数学课程将概率推到了学生的面前。“统计观念”（ 含“概率直觉”）做为一种基本的数学核心素养引入中小学课程体系，已经成为国际数学课程改革的一个趋势。

1.小学数学“概率”课的教学和探索的意义。

生活中我们经常会听到“天气预报说，今天可能会下雨”、“我买了好多彩票都没中，中奖率太低了”、“我打赌，这次考试小明一定会输给李刚”等语言，这实际上就是人们对客观世界某些现象的一种描述，其中涉及大量的数学信息。学生在学习概率的过程中，不仅整理和分析信息的能力得到增强，而且随着学习的深入，体验到有些事件的发生是确定的，有些则是不确定的；知道事件发生的可能性是有大小的；会对简单事件发生的可能性作出预测，并阐述自己的理由。从而逐步形成“概率直觉”，养成尊重事实的科学态度。

2.“四步式”小学数学“概率”课教学模式

基于“概率课”教材的特点和小学生认知发展规律，并结合实际教学经验，我尝试构建“四步式”小学数学“概率”课教学模式：猜测—验证—旁证—结论。

猜测：在通过各种活动让学生亲身经历对随机现象的探索过程中，引导学生首先猜测结果发生的概率，哪些是一定的、哪些是不可能的、哪些是可能的。在可能发生的事情中，哪种情况发生的可能性大、哪种情况发生的可能性小。同时让学生说明自己猜测的理由和根据。

验证：组织学生亲自动手进行实验，收集实验数据，分析实验结果，并将所得结果与自己的猜测进行比较。

旁证（辅证）：一次实验不能妄下结论，借助前人实验成果或事实进行佐证。

结论：根据实验结果，得出有关概率的结论，并逐步建立概率模型。

例如：教学人教版五年级上册“可能性”时，教学过程可以按此模式设计：

2.1 创设情境，合理猜想，激发兴趣（猜测）。

创设足球赛裁判“抛硬币”情境。

提问：任意抛一次硬币，猜猜会抛到哪一面？正面和反面朝上的可能性会怎样呢？

学生自由猜测，师引导猜测的合理性。

2.2 学生分组试验，收集并分析数据（验证）。

试验一：教师抛一次硬币。

体会：事件发生的随机性和结果的客观存在性。

试验二：等分小组，在相同的试验条件下，每人试抛2次硬币。

引发学生质疑，再次体会事件发生的随机性，并引发认知冲突，我们的猜想正确吗？怎样才能推测我们的猜想正确呢？

试验三：等分小组，在相同的试验条件下，每组试抛40次硬币。

收集数据，统计数据，计算比值，制成折线统计图。

指导学生看统计图表，初步体验比值（频率）会比投硬币的次数的一半高或低，但基本在二分之一附近摆动。

2.3 补充资料，正确推断，理解概率（旁证）。

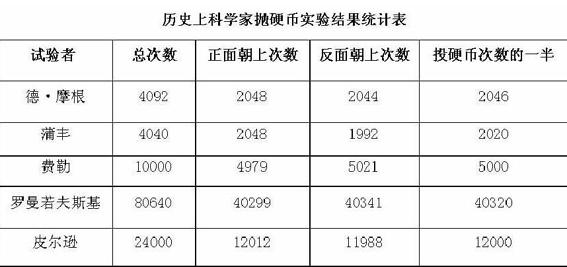
出示科学家实验的数据表，进行推断。

2.4 根据实验结果，得出正确结论，建立概率模型（结论）。

结论：抛的结果只有两种可能，而且这两种结果的可能性基本相等。

学生在此学习过程中不断将自己的最初猜测、实验结果和通过概率模型预测的结果进行比较，这将促进他们修正自己的错误经验，建立正确的概率直觉。

3.在运用“四步式”教学模式需注意的问题

3.1 必须为学生提供现实性的学习背景。数学即生活，现实生活是孕育数学的沃土，概率的教学内容同样也源于学生的现实生活世界，因此在教学中要捕捉生活背景与学习材料之间的内在联系，以学生喜聞乐见的贴近学生现实的生活情境来呈现，帮助学生用生活中的经验和实例学习数学，理解数学，感受数学。如：在教学“游戏的公平性”时，可以这样唤醒学生已有的常识和经验：同学们玩过飞行棋吗？一般用什么方法决定谁先走的呢？学生有回答用剪刀、石头、布的，有用掷硬币的，有猜手心手背的等。这种可以决定谁先谁后的经验在儿童中是经常用到的游戏规则，也是这节课中“公平性”的生活原型。

3.2 重视学生试验经验的积累，体验“可能性”。数学教学中要充分考虑学生主体性的发挥，为学生进行数学活动提供充分的思维空间和从事数学活动的机会，让学生亲历“做数学”的过程，这在可能性的探究中表现更为明显。可能性研究的是随机事件发生偶然性中的必然规律，所以如果不经历随机的体验过程，学生是很难建立相关观念的。通过随机试验、数据分析和结论推断，可以让学生体验日常生活中存在大量不确定性现象，有些事情可能发生，有些事情不可能发生，分析这些现象可以找到规律，渗透随机和概率思想。

3.3 正确处理试验时的“极端”数据。随机事件的统计规律，实际上要排除大幅度偏离实验事实的极端情况，因为这些情况的发生在大量的试验中将是小概率事件。但学生没有系统的概率知识，这无法和他们解释。当他们面对自己手中杂乱的10次或40次的试验结果，找不到规律，思考就会遇到障碍。为了帮助学生跳出困境，教师可以引导学生将数据累积起来看：10次、40次、160次……再联系历史上数学家的试验数据，并启发他们以抛掷的总次数为“参照物”，用相对的眼光来观察数据，从而发现随机事件的统计规律。这样组织学生体验可能性，更符合概率的思想。