船上大型钢管桁架结构有限元分析及优化

姜 惠 张少雄 吕 雷 程 哲

(武汉理工大学交通学院 武汉 430063)

0 引 言

钢管桁架结构作为一种典型的空间结构体系，由于其具有较好的力学特性，加上钢管加工的便利性，能带来明显的经济效益，在实际工程中已得到广泛应用[1].但大型钢管桁架结构在船舶上的应用较少，船舶规范并没有对其强度和稳定性提出要求，因此，对船上大型钢管桁架结构的强度和稳定性进行分析，研究船舶对其的影响，具有很强的实际意义.

本文以某船上的大型钢管桁架遮阳棚为例，利用有限元分析软件MSC.Patran /Nastran，建立有限元模型，参考文献[2]确定载荷及工况；分别对遮阳棚的独立模型和与船体的整体模型进行有限元分析，并对其强度、刚度和稳定性进行评估.对比两种模型的应力结果；以桁架结构质量为优化目标，对遮阳棚进行结构优化设计，其中强度、刚度及稳定性评估参考文献[3]的有关要求进行.

1 钢管桁架遮阳棚的有限元模型

1.1 模型的建立

本遮阳棚布置于船舶上层建筑的顶层甲板，结构采用钢管桁架体系，共包括49榀(横向)桁架，各榀桁架间距2.4 m，全长约97 m.桁架间设置纵向桁架9道.桁架梁采用平面梯形钢管桁架.遮阳棚上方安装压筋隔热波钢瓦.桁架、立柱的所有杆件均为圆钢管截面[4].

采用三维有限元模型真实模拟遮阳棚的空间结构，坐标采用右手坐标系，原点取在Fr93中纵剖面基线处；X轴沿船长方向，向艏为正；Y轴沿船宽方向，向左舷为正；Z沿高度方向，向上为正.钢管桁架、立柱采用梁单元建模，波钢瓦采用板单元建模.材料选用Q235钢，弹性模量为210 GPa，泊松比为0.3，密度为7 850 kg/m3.遮阳棚有限元模型见图1.

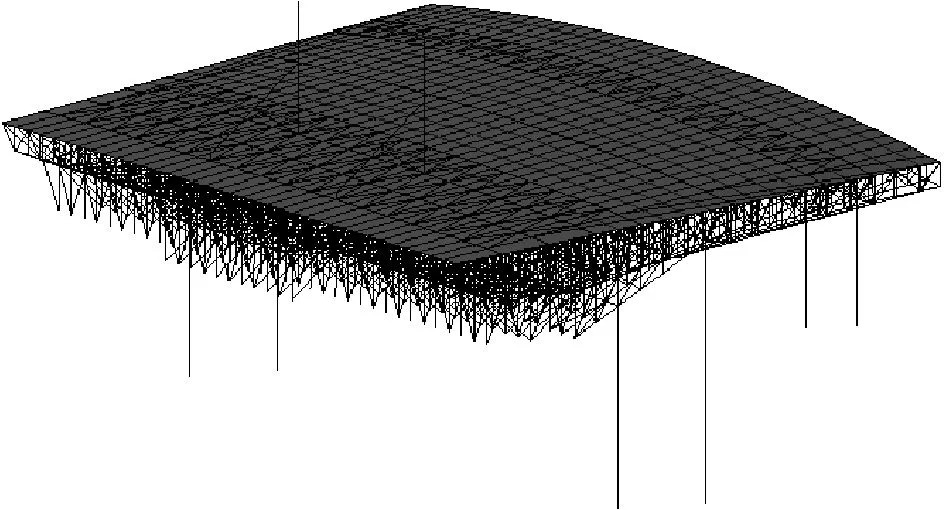
图1 遮阳棚有限元模型

为研究船舶对钢管桁架结构强度及稳定性的影响，同时选取整船模型进行分析.整船有限元模型见图2.

图2 整船有限元模型

1.2 载荷及计算工况

本文根据文献[2]和实际情况考虑遮阳棚结构所受到的各种设计载荷.按顺风(从船尾吹向船首)、横风(从左舷吹向右舷)和横风(从右舷吹向左舷)三种风向可分为3种工况，各工况下遮阳棚上的载荷汇总见表1.

表1 遮阳棚载荷

上述计算得到的雪载荷、风载荷都是载荷标准值，在施加时，所有计算得到的雪载、风载都乘以1.4的载荷分项系数，再施加到模型上.

1.3 边界条件

单独计算遮阳棚模型，模拟其在陆地上的情况.遮阳棚底部采用固支边界条件，即ux=uy=uz=0，θx=θy=θz=0.

1.4 强度校核标准

根据文献[3]中钢材的强度设计值的要求，厚度小于16 mm的Q235钢强度设计值为215 MPa.

1.5 刚度校核标准

在桁架设计中，采用限制构件长细比的办法来保证其刚性.根据文献[3]可知，长细比为

(1)

式中：l为杆件计算长度，腹杆取0.8倍的几何长度，弦杆取相邻侧向支承点的间距；r为有效回转半径.许用长细比拉杆[λ]=200，压杆[λ]=150.

1.6 稳定性校核方法

1.6.1桁架的稳定性

根据文献[3]对桁架中弦杆、腹杆等构件的稳定性按轴心受力构件进行校核.规范公式中考虑了构件的初始缺陷、允许截面存在一定的塑性发展，采用式(2)进行稳定性计算[5].

(2)

式中：N为杆件轴心应力；A为截面面积；φ为轴心受压构件的稳定性系数；f为抗压强度设计值.

1.6.2支柱的稳定性

根据文献[3]对桁架中支柱的稳定性按压弯构件进行校核.规范公式依据弹性压弯构件边缘屈服准则，综合考虑构件截面的塑性发展、二阶弯矩、初弯曲和残余应力的影响，采用数值计算的方法[6]，根据式(3)对支柱在弯矩作用平面内稳定性计算：

(3)

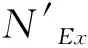
当构件在弯矩作用平面外没有足够支撑来限制其产生的侧向位移和扭转时，构件可能发生弯扭屈曲破坏，需要对支柱平面外稳定性进行校核[7].

弯矩平面外的稳定性计算式为

(4)

式中：φy为弯矩作用平面内的轴心受压构件稳定系数；φb为均匀弯曲的受弯构件整体稳定系数；Mx为所计算构件段范围内的最大弯矩；η为截面影响系数；βtx为等效弯矩系数.

2 计算结果及分析

2.1 强度及长细比校核

利用软件MSC.Nastran分别对遮阳棚的独立模型和与整个船体的整体模型进行有限元分析.3种工况下，两个计算模型的最大应力值见表2.选取不同剖面、尺寸最长的单元进行刚度校核，长细比校核结果见表3.

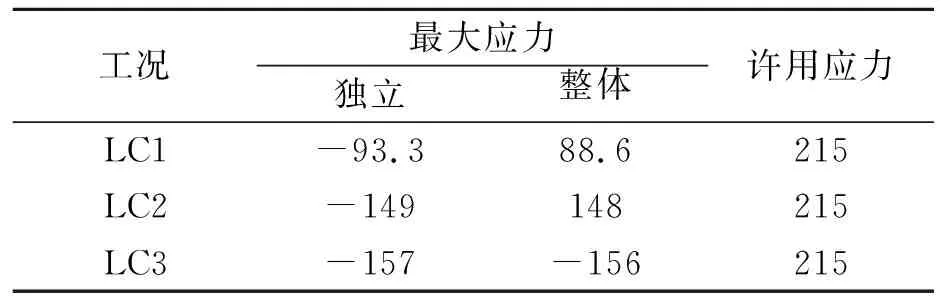
表2 各工况下，两模型的最大应力 MPa

表3 长细比校核结果

1) 从表2～3可知，两种模型所有工况下遮阳棚结构的计算应力均小于许用应力，所有构件均满足长细比的要求，因此该桁架满足材料强度与结构刚度要求.

2) 上述三种工况中，两个模型的最大应力均出现在工况LC3，此时风向为顺风，其对应的应力云图见图3～4，最大应力均出现在右舷船中部的横向腹杆上.

图3 工况LC3独立模型梁单元的轴向应力云图

图4 工况LC3整体模型梁单元的轴向应力云

2.2 稳定性校核

对两种计算模型所有工况下桁架结构的所有杆件的进行稳定性校核，将各工况的最大计算应力列于表4.

表4 稳定性校核结果 MPa

1) 由表4可知，两种计算模型所有工况下支柱的稳定性均满足要求，且计算应力与许用值比余量较大，可进一步优化设计.

2) 两种模型工况2～3都存在杆件稳定性不合格的情况，不合格的杆件皆为右舷船中处的横向斜杆，尺寸为直径×壁厚：168 mm×10 mm.将不满足稳定性要求的杆件的尺寸加强为直径×壁厚：219 mm×10 mm，加强后，本桁架结构所有杆件均满足稳定性要求.

由强度和稳定性校核结果可知，最危险的工况为顺风工况.在此工况下，对于轴向应力、弯曲平面内应力和弯曲平面外应力，将整体模型应力计算结果减去独立模型应力计算结果，不同差值范围内杆件数量占所有杆件总数的百分比见表5.

表5 不同差值范围杆件所占百分比

由表5可知，对于轴向应力，该桁架结构65%的杆件在整体模型下应力计算结果大于在独立模型下应力计算结果，其中63%的杆件其应力差值在0～40 MPa；而对于弯矩平面内应力和弯矩平面外应力而言，约50%的杆件在整体模型下应力计算结果大于在独立模型下应力计算结果，差值基本在0～40 MPa，大于40 MPa的杆件数量可忽略.表明钢管桁架结构与在与船体连接成整体后和单独计算相比，大部分杆件稳定性计算应力变大，整体结构稳定性能变差，即该桁架结构在船上比在陆地上更易失稳.因此，在对此桁架结构单独进行稳定性校核时，应使独立模型的稳定性计算应力控制在175 MPa以内，留有20%的稳定性应力余量，保证该桁架结构与船体相连接进行整体计算时，满足稳定性要求.

3 钢管桁架遮阳棚的优化设计

按照本船结构直接计算所得应力水平和分布，初始设计的桁架结构中各种杆件的强度和稳定性都有一定的优化空间.

3.1 结构优化方法

结构优化设计指的是在结构形式确定以后，对结构尺寸、外形参数等进行优选，找到一种满足要求的最佳方案设计.对于复杂和大型结构的优化，是以有限元计算为基本手段，以最优化算法为搜索导向，通过数值计算的方法得以实现.

桁架结构的重量越轻，制造成本就越低，对船舶的影响就越小.因此在保证桁架结构强度、刚度及稳定性满足要求的情况下，以减轻结构重量作为优化目标，以水平斜杆和纵向弦杆和斜杆的尺寸为优化变量，通过MSC.Patran/Nastran对桁架结构进行优化设计[8].

具体的优化方法见图5[9].

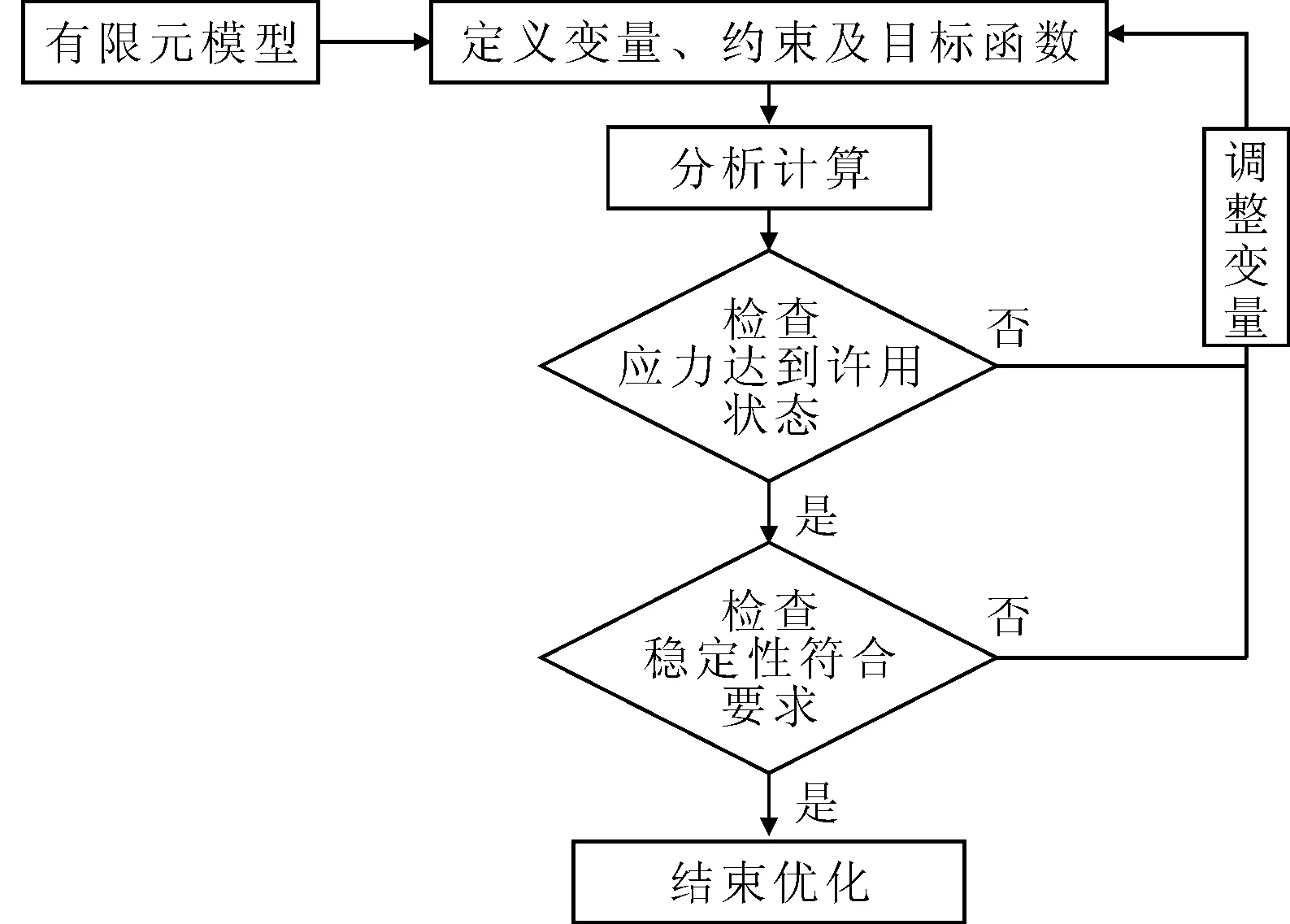
图5 优化流程图

3.2 结构优化结果

利用Nastran进行有限元分析，经历多次循环，得到了优化方案，分别计算独立和整体模型，优化前后的数据对比见表6[10].

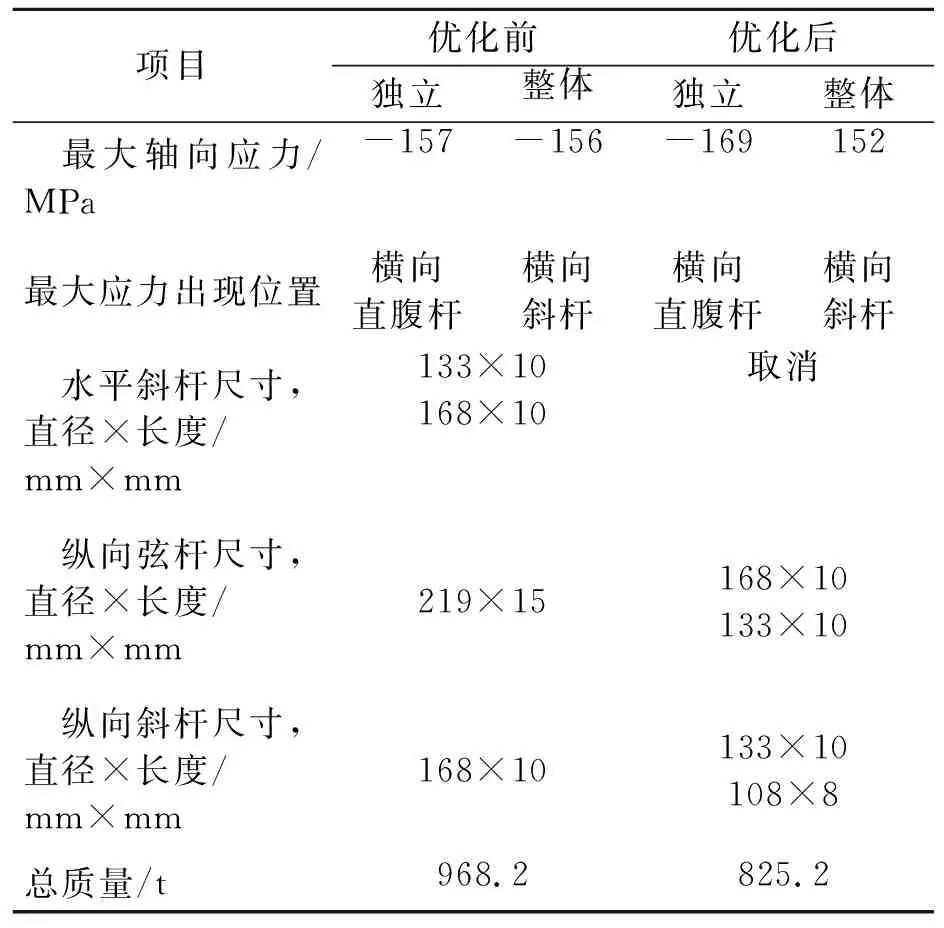
表6 优化前后数据对比

由表6可知，两个模型优化后的最大应力均变化不大，均在许用值之内，出现的位置也基本不变，可以作为桁架设计的参考.优化后桁架结构质量为825.2 t，较优化前的968.2 t减轻约15%.优化结果表明，通过合理的调整结构尺寸，进行尺寸优化，可以有效的实现降低结构重量，减小结构内部应力的目的.

4 结 论

1) 用两种模型分别对桁架结构进行强度分析和稳定性校核，结果表明，加强后该大型钢管桁架结构满足规范要求，但局部构件存在高应力情况.两种计算模型的高应力都主要集中在右舷船中处的横向(斜)腹杆，在设计和建造时应加以重视.

2) 船舶变形对桁架结构应力状态的影响较大，使其更加危险.对类似的船上钢管桁架结构可以先采用独立模型，模拟其在陆地上的情形，进行强度、刚度和稳定性的校核，但必须留有合适的应力余量.在保证独立模型的应力余量约20%的情况下，采用整体模型计算桁架结构也能满足规范要求.

3) 采用MSC.Patran/Nastran软件对桁架结构进行有限元分析及优化，在满足强度、刚度和稳定性要求的基础上，通过优化纵向构件和水平构件的尺寸，使桁架结构质量减少143 t，减轻约15%，受力更加合理，对类似船上的大型桁架结构设计具有一定的参考意义.