基于有限元的分析与配筋法在双排桩-锚杆 结构设计中的应用*

董必昌 田智睿付绍卿 王 宇

(武汉理工大学交通学院1) 武汉 430063) (武汉中科岩土工程有限责任公司2) 武汉 430063)

0 引 言

桩锚支护是一种常见的深基坑支护方式[1]，这种支护结构通过锚杆对排桩提供锚拉力，从而减小支护排桩的位移与内力，并将基坑的变形控制在允许的范围内.相比其他支护结构，桩锚支护不需加设内支撑，具有变形小、施工简易等优点，在深基坑工程中得到了广泛应用.

对于门式双排桩-锚杆支护结构的设计和受力分析，王惠民等[2]采用有限元软件，基于Mohr-Coulomb模型，对双排桩-锚杆支护结构深基坑的开挖全过程进行了数值模拟研究，发现开挖完成时,在桩身中部附近产生最大水平位移；基坑外超载对基坑支护影响很大.胡海军[3]通过数值模拟的方式，分析了支护结构在土体开挖荷载作用下的内力和变形，为其设计和施工提供了参考.胡贺祥等[4]采用适用于敏感环境下基坑数值分析的硬化类弹塑性本构模型，针对锚杆对双排桩变形和受力的影响进行数值模拟，发现锚固角度的增加能有效减小双排桩的最大水平位移和后排桩的桩身控制弯矩，但减小幅度随锚固角度增大而减小.谢荣昌等[5]结合具体工程实例分析了实际监测数据，证明了双排桩桩锚支护体系在紧邻高层建筑深基坑支护工程中的适用性，为同类工程的方案设计与施工提供参考.上述研究主要通过数值模拟等方法探讨了门式双排桩-锚杆支护结构的受力特征和工程应用，而对于该结构的配筋设计研究涉及较少.在实际工程中，双排桩-锚杆结构的受力机理较为复杂，文献[6]中将双排桩假定为平面刚架结构进行计算，这种假定用于双排桩-锚杆这种特殊结构时还不够合适，故相关配筋计算结果偏向安全和保守.因此，本文以门式双排-锚杆支护结构为例，基于有限元法，对其受力特征和配筋设计进行了研究，并得出了相关结论.

1 双排桩锚结构数值模拟

1.1 模型概况

选取武汉时代广场深基坑桩锚结构支护体系进行仿真模拟，该工程项目处于汉口沿江大道兰陵路与黎黄陂路之间.其场地位于长江左岸一级阶地上，有着较为稳定的二元地层结构，上部土层主要为静水沉积相黏性土，下部为为长江冲洪积相砂类地层.下伏基岩为志留系泥岩.双排桩影响范围内地质土层自下而上依次为粉砂层，粉土层，粉质粘土层，填土层.

基坑开挖深度为16.4 m，采用桩锚支护.支护桩为钻孔灌注桩，靠近基坑一侧为前排桩，靠近土体一侧为后排桩，桩间土采用旋喷处理，桩长为22 m，桩径为0.9 m，桩心距为2.8 m，桩身嵌入土层8.6 m，约为整个桩身长度的2/5.锚杆设置为三排平行布置，采用预成孔二次注浆锚杆，预应力张拉锁紧，锚索位置见表1.

表1 基坑预应力锚杆参数

对于模型的计算范围，以双排桩为中心，在横向宽度(X方向)：底边长度为65 m，前排桩桩顶到左边界的距离为30.5 m，后排桩桩顶到右边界的距离为30.5 m；在横向高度(Y方向)，左端边界高为24.7 m，右端边界高为41.1 m.深基坑支护模型见图1，双排桩和锚杆尺寸见图2.

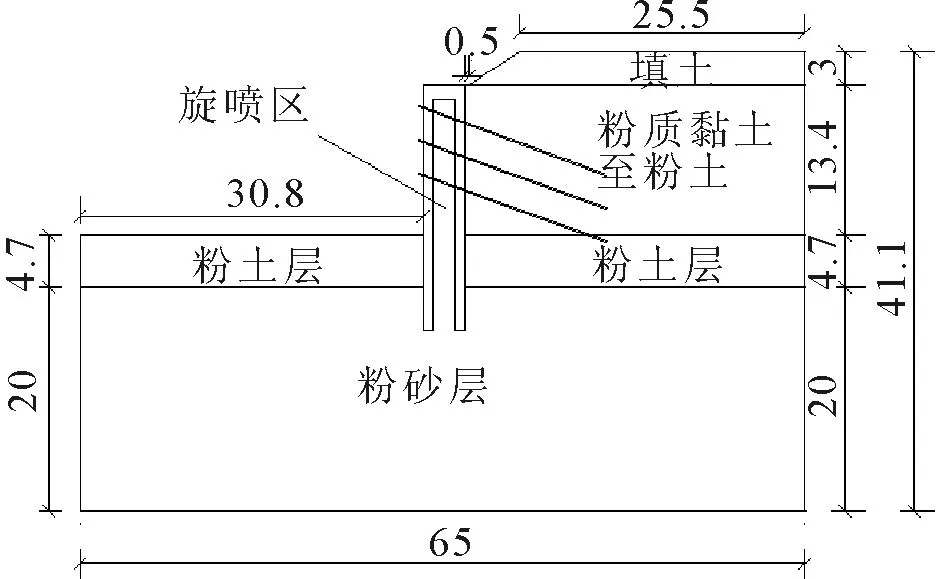
图1 基坑支护示意图 (尺寸单位：m)

图2 双排桩和锚杆尺寸图 (尺寸单位：m)

1.2 模型建立

由于本文主要对深基坑和支护桩进行水平方向受力研究，故建立支护结构的平面模型，且不考虑桩土接触.模型中土体和双排桩均采用PLANE82单元模拟，对于基坑土体的本构模型，采用理想弹塑性模型，屈服准则采用Drucker-Prager[7]准则，双排桩和桩身之间的旋喷区采用线弹性模型，且对桩身端部的周边单元进行网格加密和平顺处理，锚杆采用LINK8[8]单元进行模拟，预应力为180 kN，通过定义LINK8单元参数来输入锚杆的截面尺寸和预应力值，将锚杆单元与桩土单元进行耦合来模拟锚杆锚定的效果.在模型的边界上，地面和开挖面为自由面，两边竖直边界水平约束，底面全约束，具体模型材料参数见表2，图3为有限元模型，图4为划分网格后的模型.

表2 模型材料参数

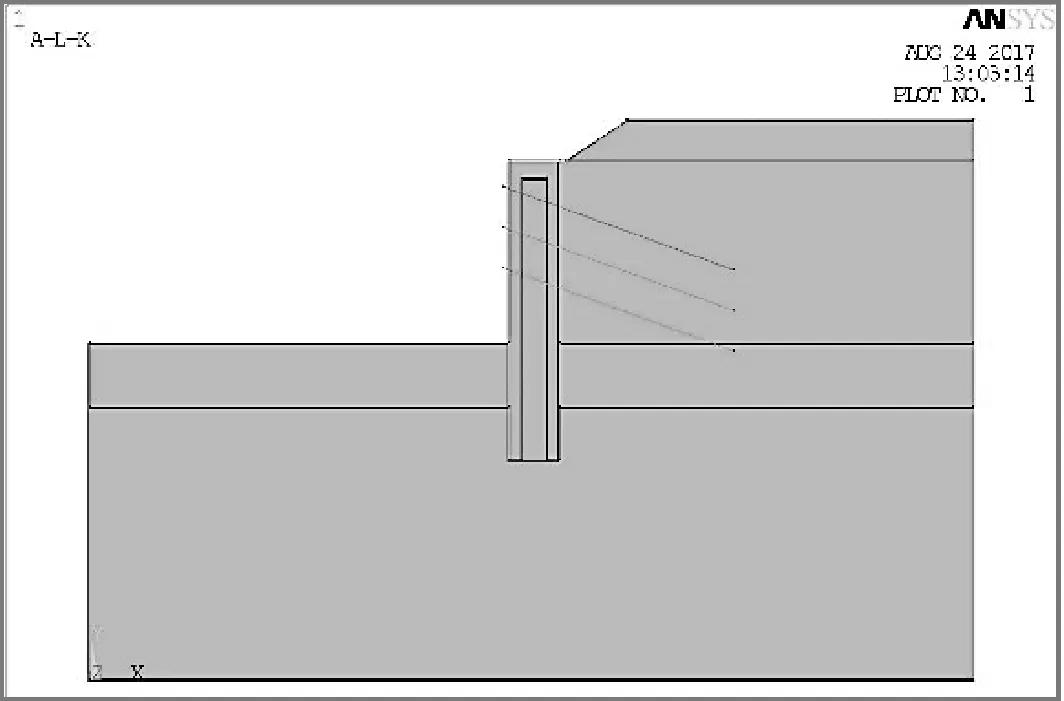
图3 双排桩边坡模型

图4 网格划分后的模型

2 模型受力特征及变形分析

2.1 基坑土体变形分析

基坑的场地土体在开挖之前就有长期的自重沉积，使得土体已达到沉降固结，为了获得基坑开挖过程中土体卸载造成的土体沉降，分别建立了基坑开挖之前与基坑开挖后模型，通过相减基坑在开挖前后的沉降值，可去除土体由自重应力场作用导致的沉降，并计算得到基坑由于卸载导致的额外沉降变形，以便于对基坑整体变形的分析.

图5为基坑开挖前和开挖后的Y方向位移云图.由图5可知，随着基坑的开挖，基坑内测边缘土体逐步出现隆起，而基坑外侧土体则因基坑内的土体卸载破坏了原有平衡重力场，从而出现沉降，对比两个模型，减去开挖前因重力场造成的沉积变形后可得到由基坑开挖造成的额外沉降为0.8 cm，小于地表沉降警戒值，满足安全需求.

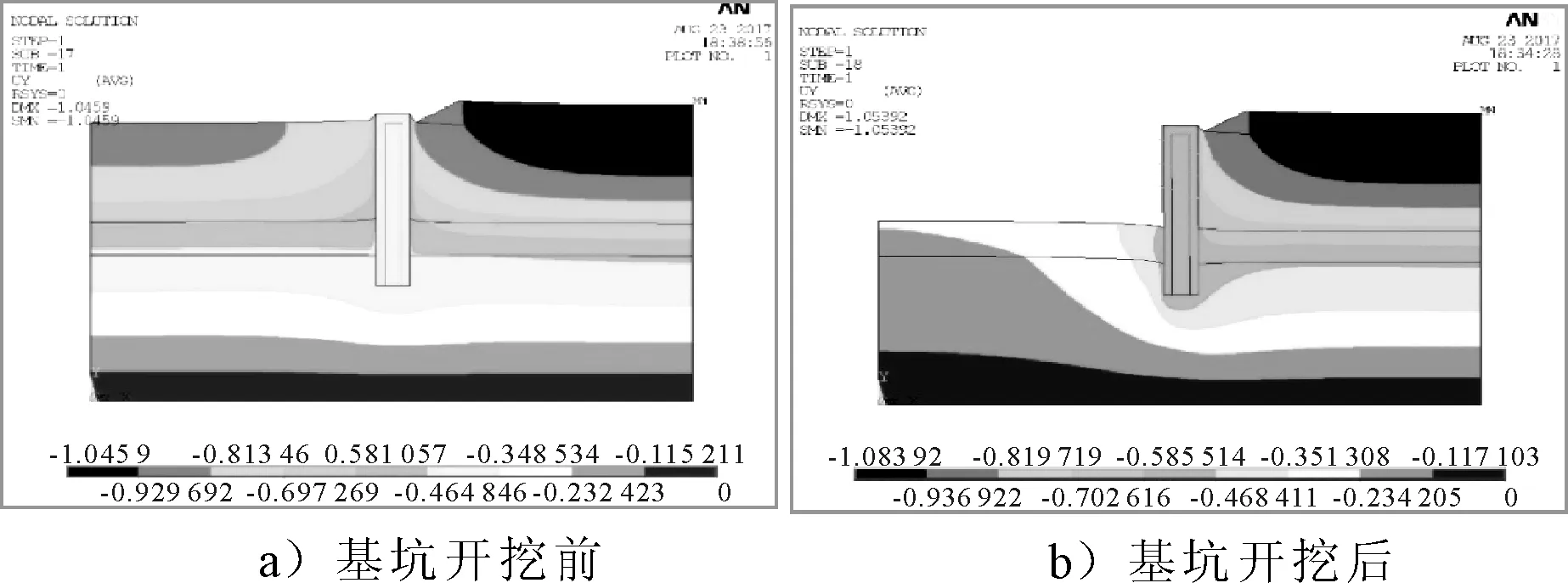
图5 模型Y向位移云图 (单位：m)

2.2 双排桩-锚杆结构受力及变形分析

随着基坑开挖，基坑内侧土体进行卸载，从而导致支护结构的内力和位移发生变化.图6为基坑开挖完成后，双排桩桩身的第一主应力云图.由图6可知，在桩身锚固处以及桩身与嵌入土体交界处应力较为集中，前排桩第一主应力最大值为2.72 MPa，后排桩第一主应力最大值为1.85 MPa.

图6 双排桩第一主应力云图 (单位：Pa)

图7为双排桩剪力云图.由图7可知，前、后排桩均在在土层分界面处存在着剪应力突变现象，其中前排桩在距桩顶18.22 m处出现最大剪应力，值为0.64 MPa；后排桩在距桩顶17.62 m处出现最大剪应力，值为0.82 MPa.

图7 双排桩剪力云图 (单位：N)

图8为锚杆水平位移云图.由图8可知，第二和第三排锚杆上出现最大节点水平位移为5 cm，且靠近锚杆埋入土层一端的节点位移较大.图9为双排桩水平位移云图.由图9可知，身在右侧土体的压力作用下向基坑内侧弯曲变形.前、后排桩均在桩顶处出现最大水平位移，前排桩最大水平位移为为2.1 cm，后排桩最大水平位移为2.0 cm.桩顶以下至基坑底部，桩身水平位移逐渐减小，表明锚杆对支护结构的变形起到了抑制作用，使结构达到了支挡土体的功能.

图8 锚杆水平位移云图(单位：m)

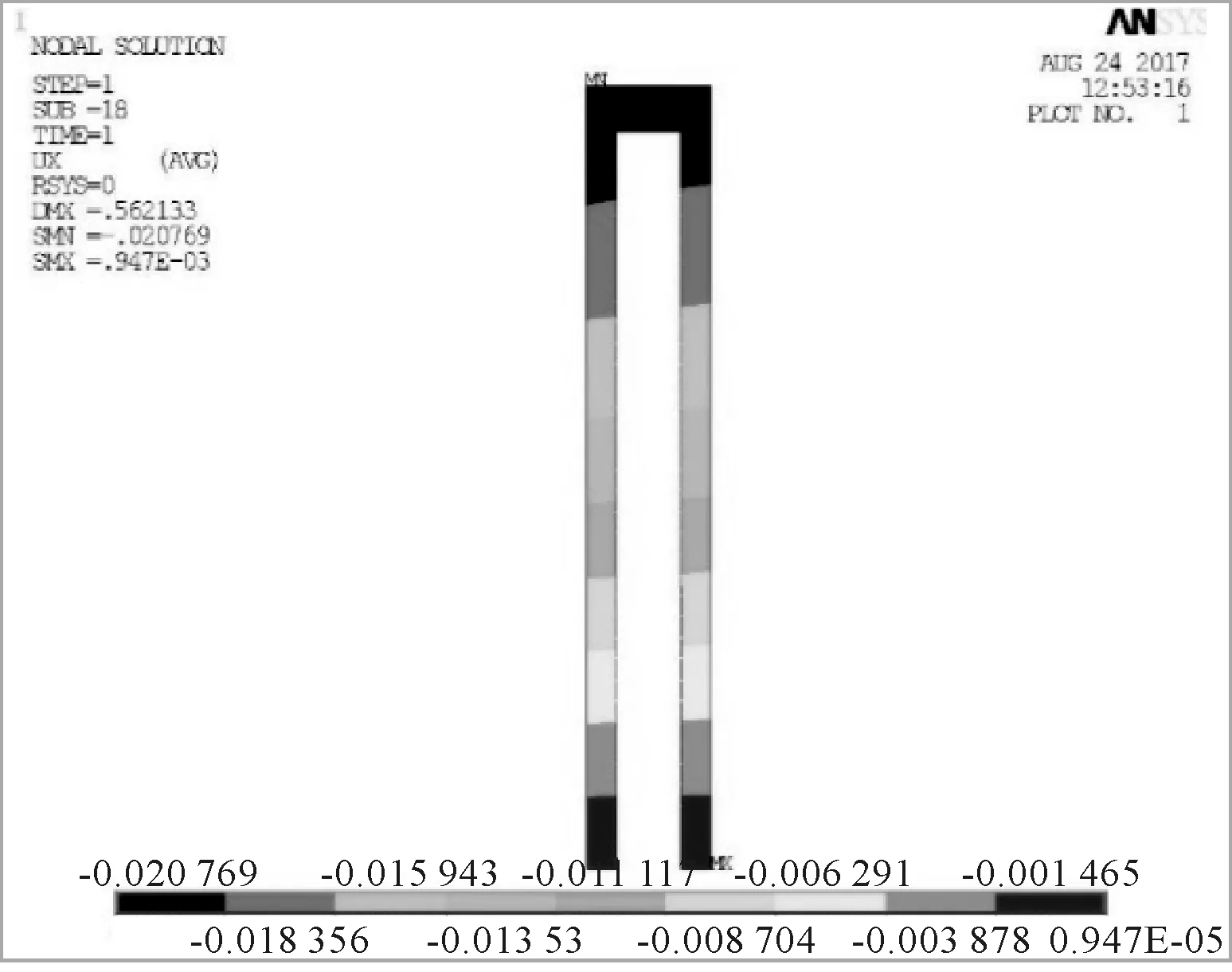
图9 双排桩水平位移云图(单位：m)

3 门式双排桩-锚杆结构配筋

3.1 基于有限元的双排桩内力计算

由于门式双排桩-锚杆结构在实际支护过程中的受力机理较为复杂，而现有规范中只是将其简化为平面刚架结构进行内力计算，这种假定用于双排桩-锚杆这种特殊结构还不够合适.而通过建立基坑支护结构的有限元模型，模型将桩作为弹性体，再根据有限元计算得出的弹性体的受力结果，便可以进行配筋.

双排桩的主筋和箍筋的配筋面积分别根据桩身所受的剪力和弯矩计算得到，考虑Ansys软件只能得出结构各个节点的应力结果，不能得出截面受力，故使用Ansys后处理功能将模型中的双排桩节点剪力以文本形式导出，采用单元节点力求和法处理节点数据，即将同一截面上的节点剪应力进行累加，从而得出该截面上的剪力，并由此可以求得桩身不同位置处的剪力.

图10为前、后排桩剪力随桩身位置变化曲线，前排桩在距桩顶11.8 m处剪力最大，为546.13 kN；后排桩在桩顶8.8 m处剪力最大，为697.85 kN.再对已经得到的剪力曲线面积进行累加积分[9]，便可以得出不同桩身截面处所受的弯矩，图11为前、后排桩弯矩随桩身位置变化曲线，前、后排桩的弯矩变化趋势一致，均为”S”形曲线，前排桩在距桩顶7.7 m处弯矩绝对值值最大，为1 534.96 kN·m；后排桩在距桩顶11.2 m处弯矩绝对值最大，为1 459.12 kN·m.

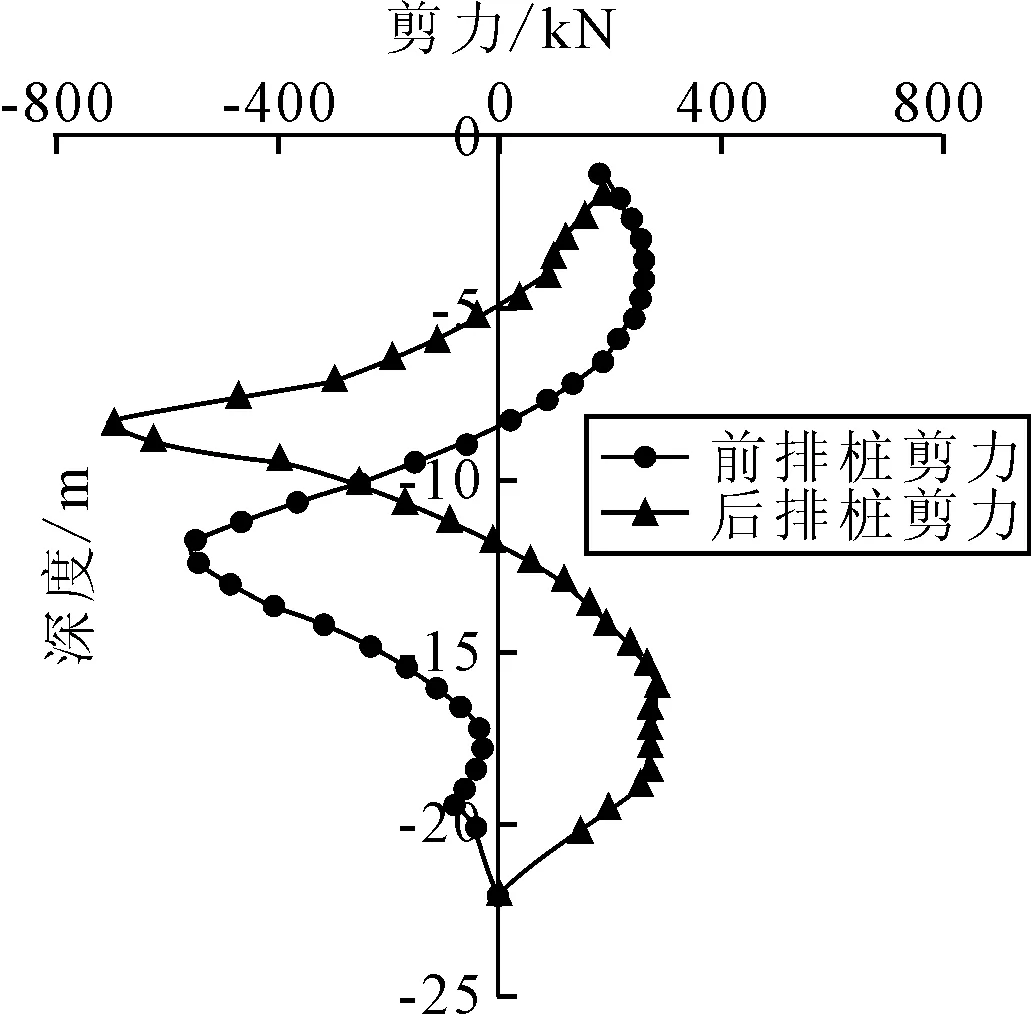
图10 前、后排桩桩身剪力图

图11 前、后排桩桩身弯矩图

3.2 双排桩配筋计算

通过处理有限元模型内力结果得出前、后排桩的最大剪力和弯矩后，便可以出现该剪力和弯矩值的截面作为最不利截面进行配筋计算.根据文献[10]中对于圆形截面桩的配筋原则对双排桩进行配筋，前排桩主筋25Ф25，箍筋Ф8@200；后排桩主筋24Ф25，箍筋Ф8@200.原工程设计采用传统方法计算，其前排桩一般截面主筋为14 771 mm2, 后排桩桩一般截面主筋为11 775 mm2；而基于有限元运算结果得到的配筋量为前排桩截面主筋12 270 mm2，比原工程设计的配筋量少；后排桩截面主筋11 775 mm2，和原工程设计一致，但考虑到原工程前后排桩在坑底4 m上下处主筋增加了12φ25，故可以得出结论：相比传统配筋方法，基于有限元的配筋法更加节省配筋用量，其前排桩截面主筋配筋量可节省23%，后排桩截面主筋配筋量可节省10%.

4 结 论

1) 随着基坑的开挖，基坑内测边缘土体逐步出现隆起，而基坑外侧土体则内测土体卸载破坏了原有平衡重力场，从而出现沉降，其最大沉降量为0.8 cm，满足安全需求.

2) 在桩身锚固处以及桩身与嵌入土体交界处应力较为集中，前排桩第一主应力最大值为2.72 MPa，后排桩则为1.85 MPa.前、后排桩均在在土层分界面处存在着剪应力突变现象，其中前排桩在距桩顶18.22 m处出现最大剪应力，值为0.64 MPa；后排桩在距桩顶17.62 m处出现最大剪应力，值为0.82 MPa.

3) 前、后排桩均在桩顶处出现最大水平位移，前排桩最大水平位移为为2.1 cm，后排桩最大水平位移为为2.0 cm.由于锚杆的抑制作用，桩顶以下至基坑底部，桩身水平位移逐渐减小.

4) 验证了基于有限元的配筋法的可行性，并发现相比传统配筋方法，基于有限元的配筋法更加节省配筋用量，其前、后排桩截面主筋配筋量分别可节省23%和10%.