KVLCC2船型限制航道中斜航水动力 及水动力导数研究*

桑腾蛟 熊鳌魁

(武汉理工大学交通学院 武汉 430063)

0 引 言

随着船舶大尺度化的发展，航行在一些限制航道区域的不安全因素越来越复杂，对于船舶安全航向构成了很大的威胁.针对限制航道对船舶航行性能影响的研究，Vantorre等[1]就不同船型进行了限制航道对于船舶水动力性能的相关实验研究.结果表明，岸壁距离越近，水深越浅，航速越快，由于岸壁效应产生的横向力及转艏力矩越大，并给出了横向力及艏摇力矩的相关经验公式.Yao等[2]根据势流理论利用Rankine源针对Wigley船型和系列60船型分别就航速、船-岸距离、水深、岸壁倾角、下潜岸壁、航道宽度等进行了系列研究，计算结果表明，当岸壁距离大于5倍船宽时，岸壁效应几乎可以忽略，而当岸壁距离小于2倍船宽时，岸壁效应表现得很明显.而对于倾斜岸壁，表明60°倾角时岸壁效应产生的横向力最大.对于下潜岸壁，则是下潜岸壁高度越高，横向力和转艏力矩则越大.李忠收等[3-4]针对系列60船型利用RANS黏性流理论采用重叠网格技术，就航速、船岸距离，以及深水和浅水两种工况进一步进行了研究，之后并对横荡，垂荡和纵摇三个自由度运动进行了研究.

本文拟针对 KVLCC2船型，利用商业软件，就岸壁距离以及水深对船舶斜航水动力计算进行相关的仿真计算,并分析不对称岸壁距离，水深，以及其联合作用对于船舶斜航水动力的作用，并且进一步研究其对于斜航水动力导数的影响.

1 基本理论

对于一般物理问题，都会遵循质量守恒，动量守恒及能量守恒三大守恒定律，文中没有考虑热交换问题且流体为不可压缩流体，所以不用考虑能量守恒定律.当流体为不可压缩流体时，质量守恒方程为:·u=0.不可压缩流体动量守恒方程p+ν2u+f；对于实际湍流问题，往往物理量都表现出一种剧烈跳动的紊流状态，使得对其计算显得十分困难，理论上物理量常表达成时均量与脉动量之和导出RANS方程由于脉动量产生的雷诺应力的求解，是RANS方程求解湍流问题的主要难点，熊鳌魁[5]提出了不同的观点.本文则主要利用商业软件自带的湍流模式求解，文献[6]对比了k-ε模型和SST-kw模型对于船舶斜航水动力问题的影响，结果表明对于斜航的水动力计算，SST-kw模型具有一定的优势.

2 模型介绍

针对 KVLCC2船型，计算模型参数与NMRI(Japan) 的实验模型相同，船长为4.97 m、船宽为0.9 m，吃水为0.323 m，方形系数为0.809 8，缩尺比为64.4.航道参数定义见图1.航道左侧距离始终取1L船长，右侧依次取1L，5B，3B，2B，1B,水深依次取5d，3d，2d；计算域船前取1.5L，船尾取3L.计算结果主要与NMRI(Japan) 的实验数据进行对比，速度与实验速度相同为0.994 m/s,弗汝德数为0.142.由于弗汝德数较小的缘故，仿真计算忽略了自由液面的影响，采用叠模的思想计算水动力.定义参考系见图2.绝对坐标系X0沿河道方向指向前方，Y0垂直指向右侧岸壁.随船坐标系位于船舯，X轴指向船首，Y轴指向船右舷；漂角β(速度方向到x轴顺时针为正，即船首指向右侧岸壁向前航行).计算结果以随船坐标为参考系并且航速始终指向绝对坐标系X0方向.

图1 航道截面定义

图2 随船坐标系定义

对于网格划分，利用商业软件将计算域划分为了近壁流域以及远场流域，近壁流域主要包含船体表面以及其边界层，由于船体表面的复杂性，采用的是非结构网格，边界层网格采用棱柱层网格，第一层网格取高1.2 mm，共三层；远场网格则利用结构网.由于网格数量较多，最终又将近壁网格转化成了多面体网格控制网格数量.计算边界入口采用速度入口，左、右、下侧壁面采用的是移动非滑移壁面，速度与入口速度相同，船体表面采用的是固定壁面，出口为outflow，上边界采用对称边界条件.

3 计算结果与分析

3.1 岸壁对于斜航的影响

计算模型水深保持为5 d，左侧岸壁距离船舶距离为1L，右侧岸壁距离依次取1L，5B，3B，2B，1B.文献[7]表明非线性水动力影响发生约在漂角10°以后，故本文选取的漂角范围在-9°～9°.其中当右侧岸壁只有1B时，由于距离比较小，漂角只能算到6°.定义水动力系数为

计算结果见图3.

图3 岸壁作用下斜航水动力

由图3可知，阻力随着漂角以及岸壁距离变化影响较小，Cx始终在-0.016～-0.018变化.而随着右侧岸壁距离的变化，横向力的不对称性表现的比较明显，艏摇力矩则表现变化不大且较对称.仅当岸壁距离为1B时艏摇力矩才表现出明显的差异.注意到漂角为0°时，不对称岸壁时的横向力不为0，主要是靠近岸壁一侧相对流速较大，压力变小对于船体产生了吸引力，且随着右侧岸壁距离变小，岸壁效应表现得越明显.特别是当岸壁距离仅为1倍船宽时，横向力作用非常明显.由图3可知，右侧岸壁距离为1L即左右岸壁对称时与实验数据吻合较好.证实了仿真计算具有一定的可信度.由于本文未考虑自由液面的影响，所以可能与实际情况有一定出入，特别是岸壁对于艏摇力矩的影响没有充分体现出来.下文拟以漂角符号为界，比较漂角为非负和非正，以及整体的水动力系数的关系，见表1.

表1 不同岸壁距离水动力导数计算

注：Yv为横向力系数相对于漂角的斜率，Nv为首摇力矩相对于漂角的斜率.

由表1可知，水动力导数Yv随着右侧岸壁距离的减小有一定增加，但是不对称性表现不太明显，仅当岸壁距离为1B时不对称性很明显，而Nv的不对称性表现不明显且仅当岸壁距离为1B时有比较大的增加.并且水动力导数随岸壁距离的减小影响不是很明显.

3.2 水深对于斜航的影响

计算模型右侧岸壁距离保持为1 L(即左右侧距离保持相同)，水深依次取5 d，3 d，2 d研究水深对于船舶斜航水动力以及水动力导数的影响，水动力系数见图4.由图4可知，阻力、横向力和艏摇力矩都对水深比较敏感，船体阻力随着水深减小先有一定的减小而后又有所增加，而斜航产生的横向力及艏摇力矩都随着水深减小而增加，并且始终保持着一定的对称性，这与实际情况是吻合的.继而计算了不同水深下的水动力导数，见表2，得出水动力导数也是随着水深减小而增加并且是对称的.

图4 不同水深斜航水动力

漂角/(°)5 dYvNv3 dYvNv2 dYvNv-9～00.005 60.002 40.006 60.002 60.00 90.003 40～90.005 40.002 40.006 60.002 60.008 90.003 4-9～90.005 20.002 50.006 60.002 70.008 50.003 4

3.3 水深、岸壁联合作用对于斜航的影响

计算模型左侧岸壁距离保持为1 L，右侧岸壁距离保持为2B，水深依次取5 d，3 d，2 d研究岸壁距离以及水深变化的联合作用对于船舶斜航水动力以及水动力导数的影响，计算结果水动力系数见图5和表3.

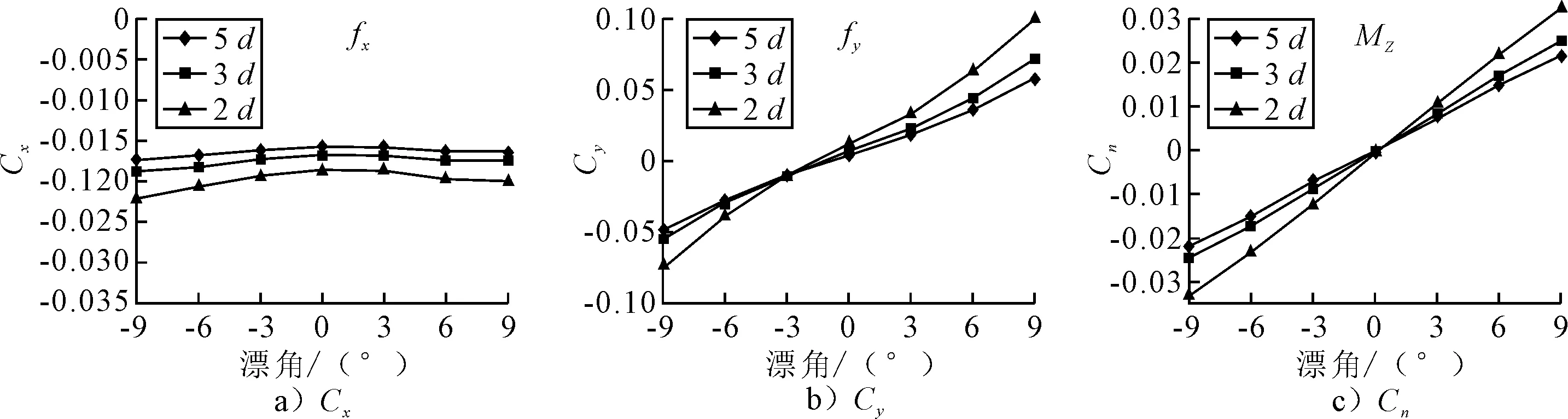
图5 不同水深、岸壁联合作用斜航水动力

漂角/(°)5 dYvNv3 dYvNv2 dYvNv-9～00.005 80.002 40.006 70.002 80.009 50.003 60～90.005 90.002 40.007 20.002 80.009 80.003 7-9～90.005 60.002 40.006 60.002 80.009 10.003 7

与第一种情况仅存在岸壁作用的情况下相比较，得出随着水深的减小，阻力，横向力，艏摇力矩以及水动力导数Yv，Nv都是增加的，这说明浅水情况下岸壁效应更加明显，见图6.而与第二种情况下即仅存在水深变化而没有岸壁作用相比较.则主要差异表现在横向力上，由于岸壁效应使得横向力不再对称，水动力导数有一定的增加但变化不是很大.继而充分说明了水深和岸壁的联合作用不单单简单的线性和.主要表现在浅水会使岸壁效应产生的横向力以及艏摇力矩更大，而水动力导数则对水深更加敏感.

图6 水深、岸壁作用下水动力导数

4 结 束 语

文中就岸壁距离、水深，以及其联合作用对船舶斜航的影响进行了计算，并对斜航时的水动力进行了比较分析，得出船舶-岸壁距离对于横向力的影响很大，而除了在岸壁距离很近时以外对水动力导数，Nv影响较小，而水深则对水动力导数的影响则很大并且浅水时岸壁效应更加明显.这对于实际船舶航行于限制水道的操纵性有一定的指导意义.由于未考虑到自由液面以及船舶运动的影响，可能会与实际情况存在一定的偏差.