基于二维非结构网格的全隐式CICSAM格式*

林 超 李廷秋 林泽华 马 麟 辛建建

(武汉理工大学交通学院 武汉 430063)

0 引 言

对流占优流动问题是计算流体力学中的一个经典问题，为此学者们发展了很多对流离散高精度格式，其中大多数格式基于结构网格有限体积法，在界面处变量值的构造涉及多个网格点的插值，而且通常与上游迎风节点有关，这很容易引起数值发散.在科学与工程问题中，格式的单调性对于求解偏微分方程十分重要，因为单调格式能够有效抑制数值振荡，避免产生非物理解.学者们对此进行了深入研究，MUSCL格式(monotonic upstream-centered scheme for conservation laws)是一种具有二阶精度的单调迎风格式，为了保证数值求解的单调性，Van[1]采用了分段多项式计算界面通量，并在其中引入了通量限制器抑制数值振荡；Harten[2]提出总残差减少(total variable diminishing，TVD)格式求解双曲线偏微分方程，通过引入r-ψ标准构造通量限制器以确保格式的单调收敛性；Leonard[3]提出的归一化变量表(normalized variable diagram，NVD)格式建立了界面f和迎风节点U之间的联系，确保了格式的单调性和有界性.这几类格式所阐述的单调性在概念上相互联系，但具体实现起来差别很大，尤其在非结构网格中实现起来更加复杂.相比于结构网格，非结构网格在构造高精度格式方面存在诸多困难，主要体现在以下两个方面：

1) 上游迎风网格单元重构 高精度格式的构造一般与上游节点有关，对于非结构网格，控制体界面f的上游第二个节点U的位置和变量值均是未知的，因此，需要对上游迎风网格单元进行重构.目前远端重构方法按插值方式可分为外插和内插两种算法，外插算法主要有Darwish′s算法、Bruner′s算法等；内插算法主要有Hou′s算法、Li′s算法和FIFSAM算法等[4-5].

2) 单调收敛性 高阶格式在处理间断解问题时，例如激波、不连续界面等问题，间断处极易出现数值振荡甚至产生非物理解，随着流动变化会继续影响流场内其他位置的精度甚至导致数值发散，如何确保格式的单调收敛性也一直是非结构网格高精度格式的难点所在.目前抑制数值振荡主要方法是通过引入通量限制器对界面插值多项式进行修正，本质上是限制数值解的梯度以避免出现数值振荡.

针对非结构网格高精度格式中所面临的问题，对于上游迎风单元的重构，文中采用一种线性插值方法重构上游迎风网格单元的空间位置，并根据顶点-单元中心间的距离加权计算上游迎风单元处的变量值.相较于上述几种远端重构算法这种方法同样可以确保格式的高精度，而且处理方式更简单有效；同时为了确保计算的单调收敛性，采用基于施主-受主通量近似思想的CICSAM(compressive interface capturing scheme for arbitrary meshes)格式离散对流方程.

1 数值方法

1.1 对流方程离散

1.1.1空间离散

对含间断解或高梯度问题的研究，采用如下二维对流控制方程的守恒形式

(1)

式中：u，v分别为x，y方向上的输运速度；φ为被输运量.

采用有限体积法离散式(1)，取任意网格控制体CV(control volume)，控制体的体积为V，将上式写成如下体积分形式

(2)

由高斯定理，体积分可以转化为面积分形式

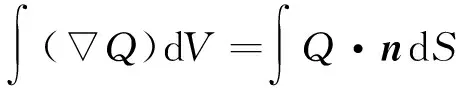
(3)

式中：Q为任意标量场；V为控制体的体积；S为控制体的封闭单元界面面积；n为方向向量，根据高斯定理式(2)可以写成面积分形式

(4)

式中：nx、ny分别为x,y方向的方向向量.将式(4)积分项移到右边，即有

(5)

式中：Un为单元面上的法向速度；Nf为控制体界面数目；Sf为界面面积.

1.1.2时间离散

传统的CICSAM格式采用具有二阶精度的Crank-Nicolson格式离散时间项，这是一种半隐式离散方法.由于隐式方法的稳定性更好，对于含间断解、大梯度突变等对流占优问题，为了确保数值解的单调收敛性，因此，本文采用稳定性更好的全隐式离散方法.

(6)

时间项采用具有二阶精度的Crank-Nicolson格式进行离散，由此式(6)可离散为如下形式

(7)

由于Pt+Δt是关于时间的函数，因此，可以对Pt+Δt进行泰勒级数展开，其在t时刻的泰勒级数一阶展开可以写成如下形式

(8)

将式(8)代入式(7)，可得

(9)

2) 全隐式离散 直接对下一时刻的对流通量Pt+Δt，以泰勒级数对时间t进行展开，有

(10)

同时，将式(10)代入式(6)，可推导为

(11)

式(9)～(10)中括号内均为常数项，等号右边项Pn中含有未知量φf，因此求解该线性方程组的关键在于求解界面值φf.前文提到界面值φf涉及多个控制体单元的节点插值，见图1.通常与上游节点有关，下面将分别介绍NVD格式、上游迎风节点的重构以及非结构网格CICSAM格式的构造.

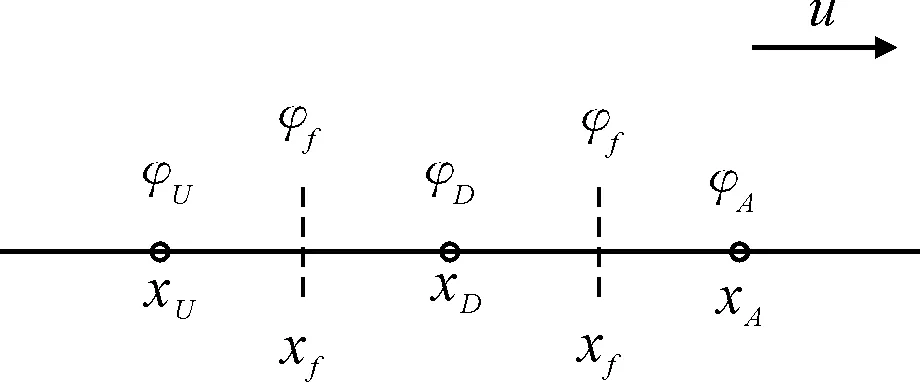
图1 有限体积法界面多点插值示意图

1.2 上游迎风网格单元的重构

对于任意形式的网格，构造具有二阶精度的对流离散格式都涉及控制体面f周围的三个网格单元，包括两个上游网格单元和一个下游网格单元(见图1)，其中U，D，A分别表示上游迎风网格单元、施主网格单元和受主网格单元.以二维三角形网格为例，见图2a)，基于线性插值的思想本文将与面f相对的施主网格单元顶点(外节点)作为迎风网格单元U，因此只需计算各单元节点处的变量值φi(i为节点编号)，见图2b)，即可得到迎风点的值φU.这种处理方法具有两个优势：①相较于传统的远端重构算法这种方法同样可以确保格式的高精度，而且处理方式更简单有效；②解决了NVD格式无法直接应用于非结构网格中的难点.

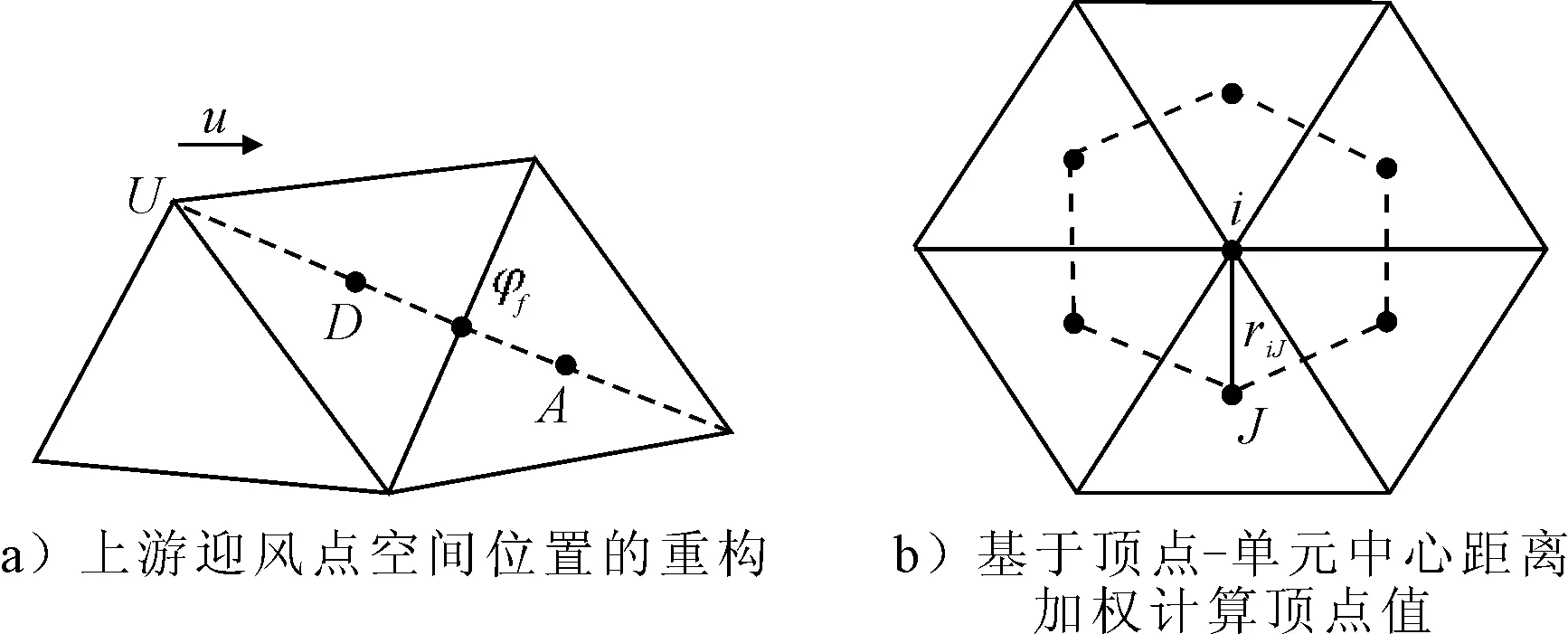
图2 上游迎风网格单元空间位置和变量值的重构

对于任意顶点i，φi计算公式为

(12)

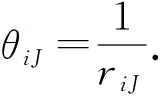
(13)

1.3 NVD格式

在结构网格中，NVD格式是构造许多现代高精度格式的基础，例如CICSAM格式、HRIC格式、STACS格式和SMART格式等；而对于非结构网格，由于上游迎风网格单元的空间位置是未知的，因此一般很难直接采用NVD格式，为此Darwish等[6]发展了一种考虑空间位置变量的NVSF(normalized variable and space formulation)格式，与NVD格式相比，NVSF格式除了需要对标量场φ进行归一化处理(见式(9))，还需对各标量场所在的空间位置x进行了归一化处理.

而本文采用线性插值方法重构上游迎风点的位置，考虑到三角形网格和四面体网格的固有特性，将与面f相对的施主网格单元顶点(外节点)作为迎风网格单元U，见图2a)，这种处理方法消除了空间位置变量的影响，因此可以认为迎风单元的空间位置是已知的，因此以NVD格式为基础构造非结构网格CICSAM格式依然是可行的，NVD格式的基本定义为

(14)

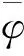
(15)

(16)

各单元中心和面上的归一化变量分布情况见图3.

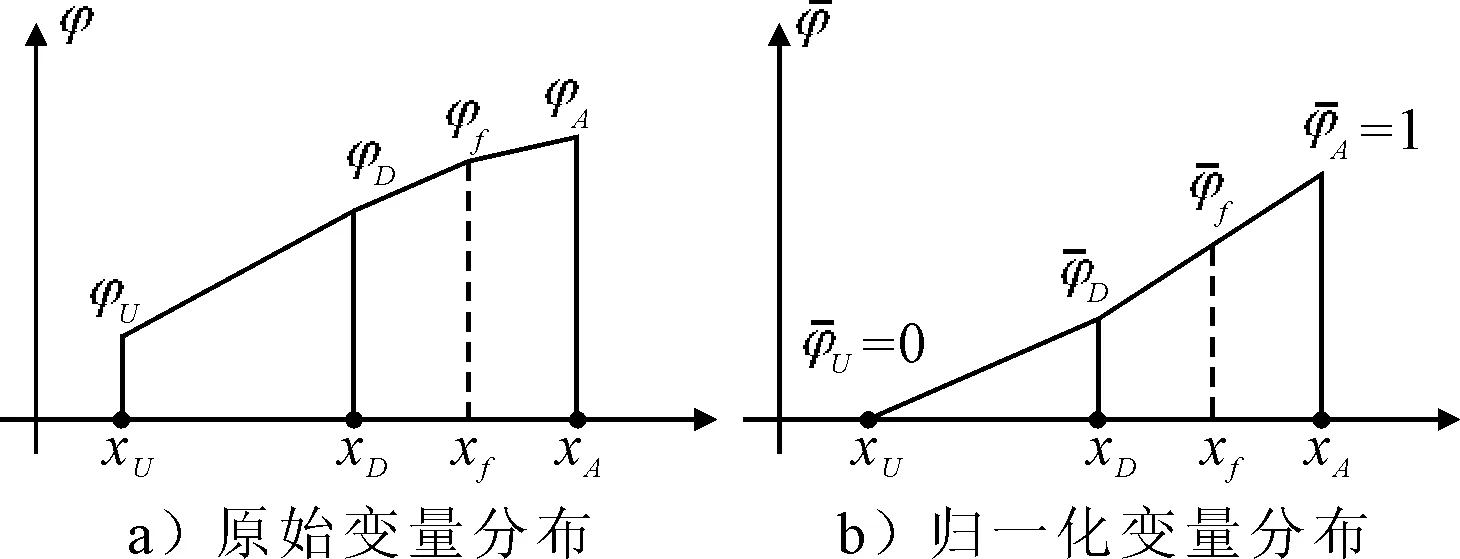
图3 原始变量和归一化变量分布示意图

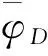
(17)

式(17)所构造的不等式关系可以表示为图4a)的有界性区域.

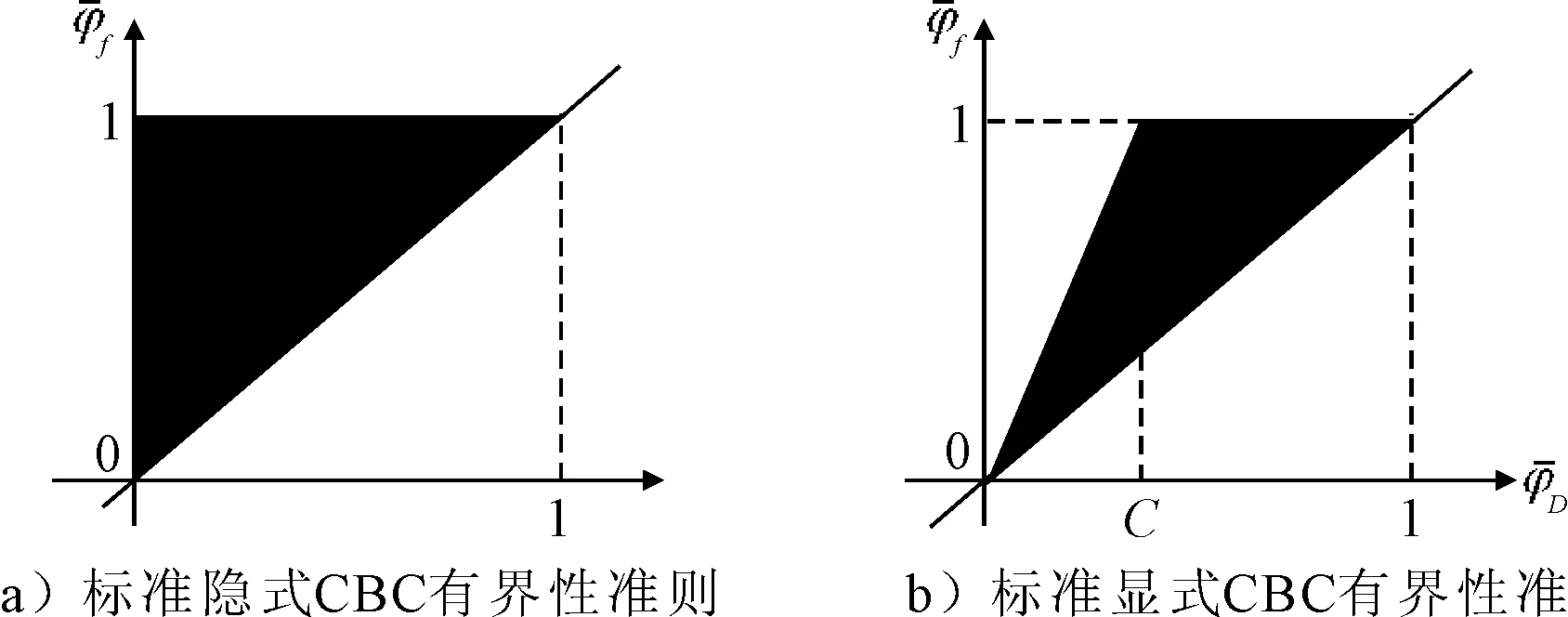
图4 CBC对流有界性准则

1.4 非结构网格CICSAM格式

在求解非定常对流方程时，库朗数是影响数值解精度的一个重要因素.为此Leonard等[8-9]引入库朗数CFL构建了显式CBC有界性准则，见图4b)，图中特征线构成的阴影区域为有界区域，这种限制准则确保了数值解的有界性.在此基础上，CICSAM格式以色散格式Hyper-C和耗散格式ULTIMATE-QUICKEST(UQ)为基本差分格式，通过权重函数f(θf)构造将两种格式进行加权组合式(18).权重函数f(θf)是关于θf的函数式(19)，θf定义为界面外法向与速度矢量之间的夹角式(20).

(18)

(19)

(20)

式中：dDA为施主网格中心和受主网格中心之间的向量；φD为施主网格中心处的梯度值.

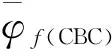
(21)

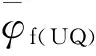
(22)

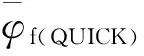
(23)

2 数值算例

为了检验本文全隐式CICSAM格式的数值精度、单调收敛性以及上游节点重构方法的可行性，选择两个经典纯对流问题进行数值验证，分别是台阶轮廓(Step-Profile)流动、半椭圆轮廓(Semi-Ellipse)流动，基本控制方程见式(1)，每个算例均给定对应的速度场.计算数值解的绝对误差，采用误差的L2范数监测数值收敛性能，为

(24)

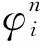
2.1 计算域和网格划分

两个算例的计算域和和网格均相同，见图5a)，计算域为1×1的正方形区域，区域内划分22 464个三角形网格单元.

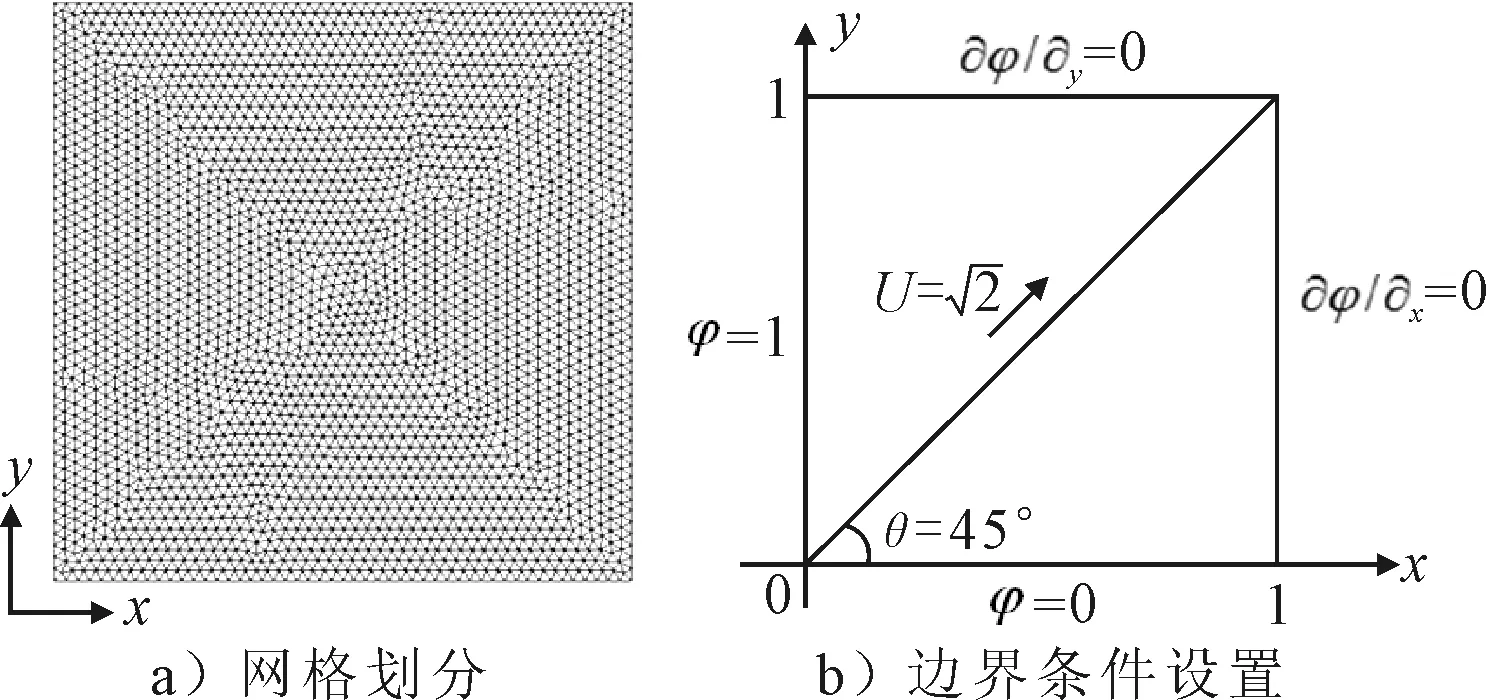
图5 网格划分与计算域边界条件设置(台阶流动)

2.2 验证算例

1) 台阶轮廓流动 台阶轮廓流动在数学物理上呈现为含间断函数的特性，存在极端边界梯度突变，隶属于间断解、非连续问题，例如空气动力学的激波问题、水动力学的自由液面问题.由于台阶流动在间断处变量的梯度发生突变，因此该算例可以用来检验算法描述突变界面的能力.

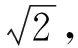
φ(0,x)=0 0≤x≤1

φ(0,y)=1 0≤y≤1

(25)

出口处的边界条件设置为Neumann边界条件，见图5b).

图6a)为x=0.7截面上不同格式数值解的精度比较，三条曲线依次表示全隐式CICSAM格式、传统CICSAM格式(半隐式)的数值解以及台阶轮廓流动的解析解，可以看出本文构造的全隐式CICSAM格式精度比传统CICSAM格式更好。

图6 全隐式CICSAM格式的精度和 收敛性验证(台阶轮廓流动)

2) 半椭圆轮廓流动 对于半椭圆轮廓流动，椭圆轮廓整体过渡平滑，但在两端仍然存在变量的梯度突变，因此该算例可以检验算法同时描述尖锐界面和平滑曲面的能力.本算例采用与台阶流动算例相同的恒定速度场、初始条件和离散方案，在入口处的边界条件设置为

(26)

出口处的边界条件设置为Neumann边界条件，见图7.

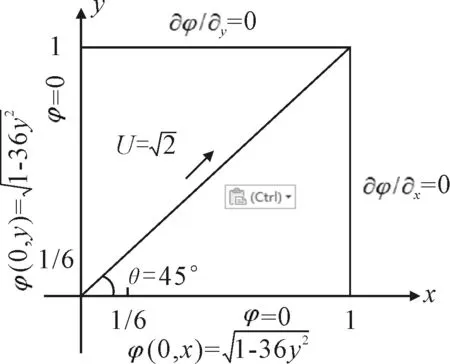
图7 半椭圆轮廓流动计算域边界条件设置

图8a)为x=0.7截面上不同格式数值解的精度比较，图8b)为的L2范数残差收敛曲线，从两个图中的结果可以得到与台阶流动算例相同的结论.

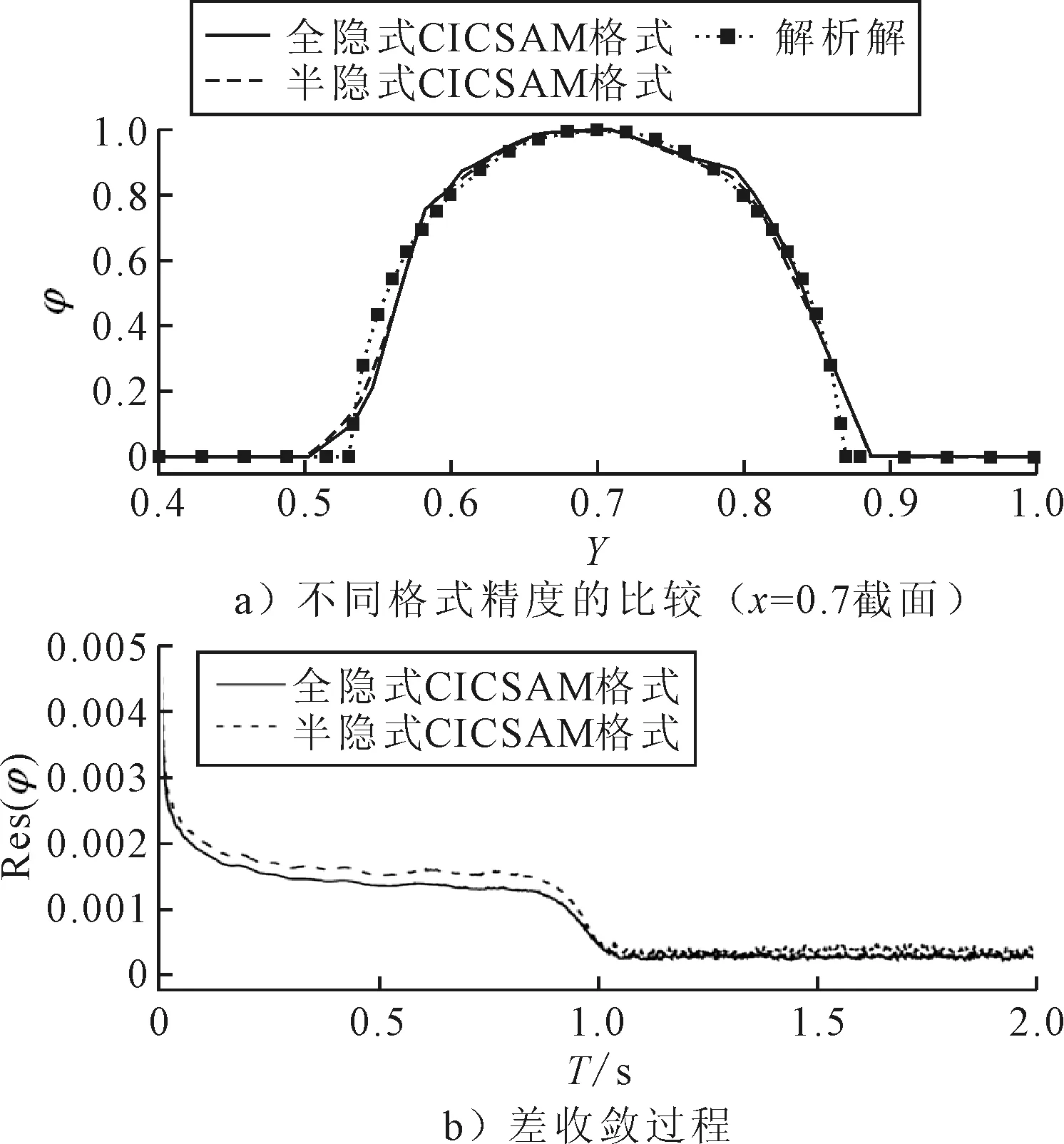
图8 全隐式CICSAM格式的精度和收敛性验证(Semi-Ellipse轮廓流动)

3 结 束 语

在NVD格式和显式CBC对流有界性准则的基础上，以色散格式Hyper-C和耗散格式UQ为基本差分格式构造了全隐式非结构网格CICSAM格式，采用线性插值的方法重构上游迎风点的位置，这种处理方法不仅简化了上游迎风节点的重构，同时也实现了NVD格式在非结构网格中的应用，这种方法也易于拓展到三维四面体网格.数值模拟结果表明，在此基础上构造的CICSAM格式实现了对梯度突变的间断界面精确捕捉，相比传统CICSAM格式其具有更好的数值收敛性能.