基于自抗扰控制的永磁同步电机速度跟踪控制

闫 峰，夏 斌，程 燃

(云科智能伺服控制技术有限公司，上海 200433)

0 引言

数控机床伺服驱动方式通常是“旋转电机+滚珠丝杠”进给方式，这种伺服形式结构复杂，且存在传动间隙及弹性变形，要获得较高的快速性和加工精度，给伺服控制系统提出了更高的要求[1]。以PID为核心的控制方法是基于系统对信号的响应特性或者系统的反馈信息来确定控制律，即利用系统的给定与实际信号的误差来确定系统的控制信号，导致系统的控制量总会慢一拍。同时，由于系统完全不依赖于模型或仅参考理想模型，当同一套控制器应用于相似的控制对象时或者是对象受到本身参数摄动和外部干扰时，控制器的参数需要重新调节，其通用性差[2-4]。文献[5]采用PDFF控制抑制速度超调，但对参数摄动和外部干扰的抑制效果不明显。文献[6]采用滑模变结构控制来抑制参数摄动和外部的扰动, 由于滑模控制固有的“抖振”问题, 影响伺服系统的稳态精度。

本文针对PMSM伺服控制系统存在的对系统参数摄动及外部干扰的抑制问题，设计线性自抗扰速度控制器(包括线性跟踪微分器、线性扩张状态观测器以及状态反馈控制器)，将非线性的系统通过状态反馈与扰动估计补偿的方式变换为一类串联积分型系统，从而提高了系统的动、静态性能。实验结果表明，线性自抗扰速度跟踪控制器可以有效地抑制不确定的扰动，提高系统的跟踪性能和鲁棒性。

1 PMSM数学模型

在忽略铁心饱和、不计涡流和磁滞损耗、转子上无阻尼绕组、永磁材料的电导率为零、相绕组中感应电动势波形是正弦波的前提下，永磁同步电机d-q轴系的状态方程为：

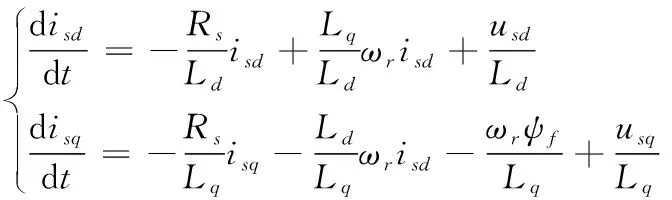
(1)

其中，isd、isq分别为d、q轴定子电流；usd、usq分别为d、q轴定子电压；Ld、Lq分别为d、q轴线圈的电感；Rs为定子相绕组电阻；ωr为电角速度；ψf为励磁磁链。

机械运动方程为：

(2)

其中，Ωr为机械角速度；Tem为励磁转矩；TL为负载转矩；J为转动惯量；B为粘滞摩擦系数。

2 线性自抗扰控制

ADRC将模型论与控制论有机的结合，通过对象模型分析，建立系统固有的加速度与系统状态的线性关系[7]。线性自抗扰控制器由线性跟踪微分器、线性扩张状态观测器以及状态反馈控制器三部分组成，其一阶线性ADRC控制框图，如图1所示。其中，v为系统输入信号；v1为过渡信号；u0为矫正信号；u为系统控制信号；z1为状态量观测信号；z2为扰动估计信号；b为系统模型参数；y为系统输出信号。

线性跟踪控制器的状态方程为：

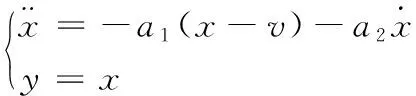
(3)

其中，x为线性跟踪微分器的状态变量；a1和a2分别为线性跟踪微分器的控制参数。当控制参数取值为a1=r2，a2=2r，且r>0时，其过渡过程没有超调。

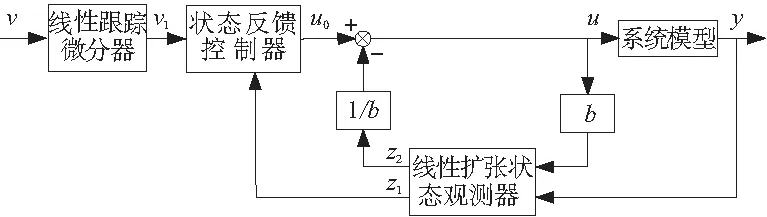
图1 一阶线性ADRC控制框图

扩张状态观测器是将系统的内、外扰动扩张成一个新的状态变量，即总扰动，并将其观测出来补偿到系统的控制量中，实现对扰动的抑制作用。

一阶非线性系统方程为：

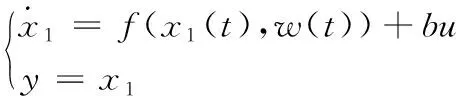
(4)

其中，x1为系统中的状态变量；f(x1(t),w(t))为系统的未建模部分及未知的扰动。将总扰动通过扩张状态观测器扩张成系统的一个新的状态变量x2=f(x1(t),w(t))，将其代入式(4)中，其线性系统方程为：

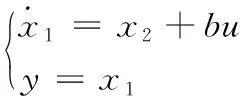
(5)

由式(4)、式(5)的推导过程，将非线性系统转换为线性系统，即为线性串联积分型系统[8]。

9）住房建设部门资料。主要为风景名胜区、自然文化遗产的名称、面积，城市（县城）和村镇建设的统计范围及相关成果资料，可作为重要地理要素的参考数据源。

由以上分析可知，线性跟踪微分器的作用是安排过渡过程，给出合理的控制信号，解决了响应速度与超调量之间的矛盾。线性扩张状态观测器通过设计一个扩张的状态量来估计未知扰动和控制对象中未建模部分，然后状态反馈控制器给出合适的控制量用于补偿这些扰动，将控制对象变为串联积分型控制对象，实现动态系统的反馈线性化。

3 自抗扰速度控制原理

一阶ADRC速度跟踪控制器框图，如图2所示。

线性跟踪控制器采用PD控制，其状态方程为：

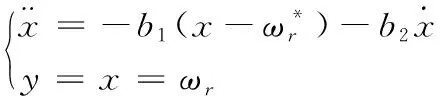
(6)

其中，b1和b2分别为线性跟踪微分器的控制参数。若使控制系统无超调，则b1=r2，b2=2r，r>0，且b1=(a1+kp)>0，b2=(a2+kd)>0，即

(7)

其中，kp和kd分别为线性跟踪PD控制器的控制参数。

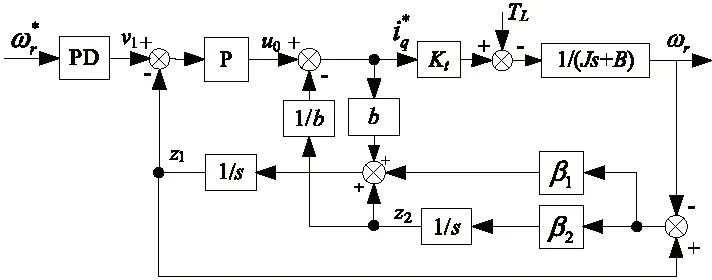
图2 一阶ADRC速度跟踪控制器框图

参考任意阶系统建立线性扩张状态观测器的方法[9-10]，建立线性扩张状态观测器的方程为：

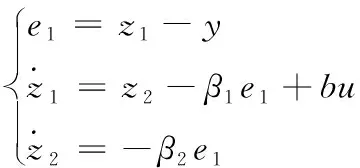
(8)

其中，e1为系统中的输出量与系统对其观测值的差值；y为系统输出信号，即为ωr；β1、β2分别为扩张状态观测器的增益参数；b=Kt/J为系统模型参数，Kt为电机转矩系数。

由式(8)整理可得，线性扩张状态观测器矩阵方程为：

(9)

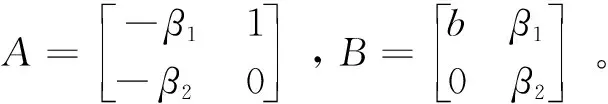
扩张状态观测器特征多项式为：

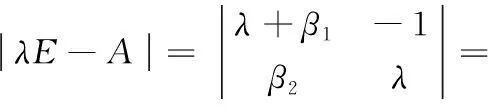
(10)

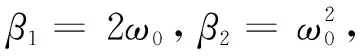
状态反馈控制器采用比例控制，其状态方程为：

(11)

线性ADRC中的扩张观测器带宽ω0和状态反馈控制器带宽ωc需要满足的条件[11]为：

ω0≈5-10ωc

(12)

通过线性扩张状态观测器可准确地将系统的扰动量、状态量及其微分值观测出来，再通过状态反馈控制器将原系统变换为“串联积分型”系统[12]。

将式(11)中的系统控制信号表达式代入式(12)中，可得：

(13)

将式(13)中的系统状态变量用x1表示，总扰动用x2表示，系统输出信号用y表示，其系统的状态方程为：

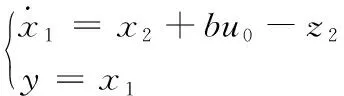
(14)

其中，变量x2和z2近似相等时，其系统状态方程简化为：

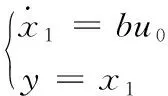
(15)

式(13)～式(15)的推导过程为控制系统对象逐渐变换为串联积分型系统的过程。

线性自抗扰速度控制器原理为通过扩展状态观测器观察出系统总扰动，然后状态反馈控制器引入合适的控制量，作为系统总扰动估计的补偿量，最后将非线性的系统变换为线性串联积分型系统进行控制。

4 实验结果及分析

永磁同步电机自抗扰速度跟踪控制系统框图，如图3所示。其中，电机采用矢量控制，电流环采用PI控制器，实验选用的PMSM参数如下：额定电压为400V，额定功率为1.3kW；额定电流为5.4A；额定转矩为8.34Nm；额定转速为1500rpm；最大电流为14A；最大转矩为23.3Nm；反电动势系数为124 V/krpm；转矩系数为1.78Nm/A；转动惯量为19.9kg·m2×10-4。采用单圈20位、多圈16位绝对值编码器获取永磁同步电机位置信息，实现闭环控制。

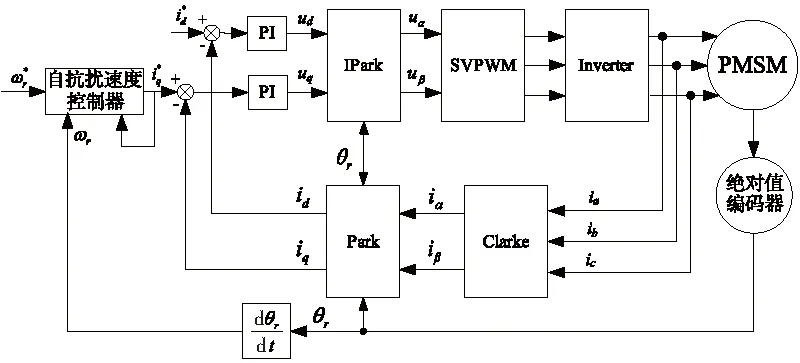
图3 PMSM自抗扰速度跟踪控制系统框图

实验采用TI的F2812DSP实现电流采样、SVPWM、SPI串行通信及双闭环控制算法等软件相关功能。采用倍福公司的EtherCAT与上位机进行通讯，获得状态变量的实验波形。

搭建对比实验平台，设计PDFF速度跟踪控制器，其控制框图，如图4所示。其中，kf为前馈补偿参数；kp为比例控制参数；ki为积分控制参数。PDFF控制参数设置值为kf=0.65，kp=30，ki=10。

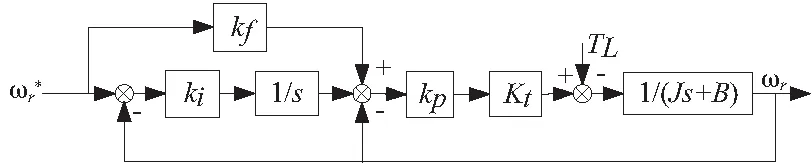
图4 PDFF速度控制框图

根据PMSM自抗扰速度跟踪控制系统框图搭建软、硬件平台，得到以下实验结果。图5分别为ADRC和PDFF速度跟踪控制系统，阶跃转速时的转速波形和q轴电流波形。图6分别为ADRC和PDFF速度跟踪控制系统在额定转速下突加、突卸额定负载时的转速波形和q轴电流波形。

由图5可得，阶跃转速指令从0rpm上升到1500rpm，ADRC控制可快速达到期望转速，且反馈转速无超调；q轴电流比PDFF控制下的q轴电流更为平滑。从阶跃转速指令跟踪特性上看，由于ADRC控制中线性跟踪微分器可优化期望指令，并给出合理的控制信号，解决了响应速度快与超调量之间的矛盾，使得ADRC控制系统具有良好的动态性能。

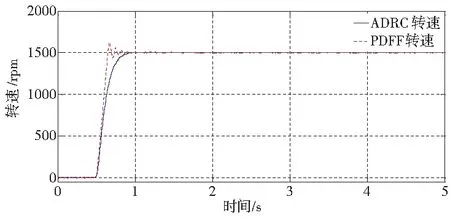
(a) 阶跃转速时转速波形

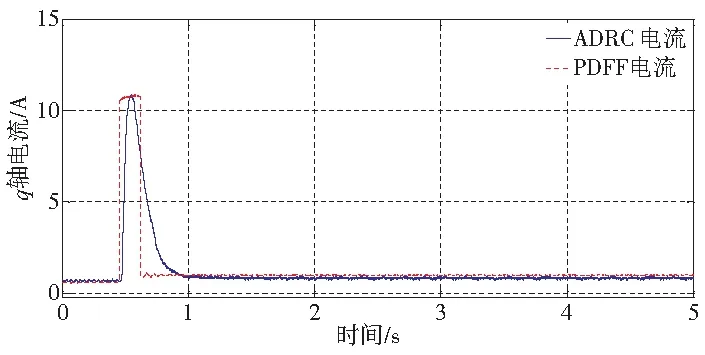
(b) 阶跃转速时q轴电流波形图5 ADRC和PDFF速度跟踪控制系统阶跃转速时转速波形及q轴电流波形

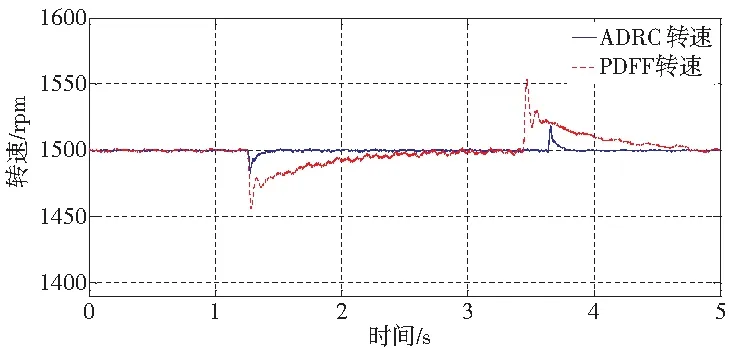
(a) 突加、卸载时转速波形

(b) 突加、卸载时q轴电流波形图6 ADRC和PDFF速度跟踪控制系统突加、卸载时转速波形及q轴电流波形

由图6可得，系统突加、突卸额定负载时，ADRC控制下的转速跌落、提升小，且可以快速恢复稳定转速；而q轴电流波形比PDFF控制的q轴电流波形动态调节更迅速且剧烈。从抗负载扰动性能上看，由于ADRC控制中线性扩张状态观测器可估算出负载扰动，而状态反馈控制器可给出合适的控制量补偿此扰动，使得ADRC控制下的速度跟踪控制系统具有良好的抗扰动特性。

实验结果表明，ADRC速度跟踪控制系统可合理地安排过渡过程，使得系统响应快且无超调。而线性扩张状态观测器和状态反馈控制器可对负载扰动进行估计和补偿，使得控制系统具有较强的鲁棒性。

5 结束语

针对高档数控机床对速度快速响应及跟踪精度的要求，结合永磁同步电机的特点，采用自抗扰控制设计速度跟踪器来抑制伺服系统模型摄动及外部不确定性扰动，实现了伺服控制系统对扰动的抑制作用。实验结果表明，该方案合理地安排了期望指令的过渡过程，并对扰动进行观测和补偿，发挥了自抗扰控制的优势，使得控制系统具有良好的动态特性和鲁棒性，从而提高了伺服控制系统的跟踪精度。