转鼓试验台路面模拟凸块研究
李艾静,王天利,朱志强,陈 双
1 引言
转鼓试验台采用结构简单的两转鼓形式,试验台系统主要由驱动电机、减速器、电机联轴器、转鼓辐板、路面凸块、传动轴联轴器,传动轴、试验台底座等部件构成,其三维模型,如图1所示。试验台主要用于模拟路面对整车施加激励,通过在转鼓上安装各种形式的凸块来模拟不同轮廓的路面[1],因此路面模拟精度与凸块轮廓密切相关。国外整车道路模拟设备技术先进,但其制造价格昂贵且使用与维护费用较高,一般仅用于整车的性能试验,因此研发出一种能够用于整车试验,且能较好地复现实际路面的耐久(可靠性)试验设备具有广阔的市场前景。转鼓试验台可以配置不同轮廓凸块使之形成多种路面激励,其结构简单、造价和使用维护成本较低,而且操作简单,使用方便,既可用于整车的性能试验也可以用于整车的可靠性试验。
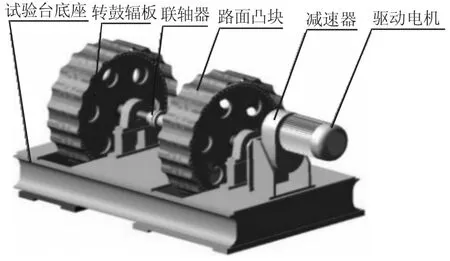
图1 转鼓试验台三维模型Fig.1 3D Model of Drum Test Rig
2 转鼓凸块轮廓设计
2.1 凸块轮廓设计原理
凸块轮廓的设计方法主要有图解法和解析法。图解法设计凸块廓线原理简单、直观易行,但绘图误差较大。采用解析法设计时需要进行大量的分析与计算,以及绘制凸块轮廓图形,借助MATLAB的数值计算功能和出色的数据可视化功能,可以方便可靠地实现转鼓型凸块轮廓线设计。
采用解析法设计凸块轮廓,需要根据路面的几何构造特点得到车轮的位移—时间运动规律s=f(t),进而得到位移—转鼓转角的运动规律s=f(φ)。列举并分析几种典型的运动规律,建立相应方程式[2]。
2.1.1 一次项运动规律
多项式类型运动规律的车轮位移方程的通式为:

式中:c0、c1、c2、…、cn—待定系数。
等速运动、等加速运动、等跃度运动、五次项运动和七次项运动等运动规律均属于此种类型。多数典型的路面轮廓曲线设计均可采用这几种运动规律进行拟合。
令式(1)中的常数c2=c3=…=cn=0,根据条件:φ=0 时 s=0;φ=φ时s=h,得c0=0,c1=h/φ。因此一次项运动规律方程式为:

式中:φ—转鼓转角,φ∈[0,φ];h—车轮周期最大位移;φ—车轮到达h对应的转鼓转角。
按上述规律,根据某汽车试验场搓衣板路面设计要求,搓衣板路面、减速带路面均可按一次项运动规律进行拟合,搓衣板凸块轮廓,如图2所示。
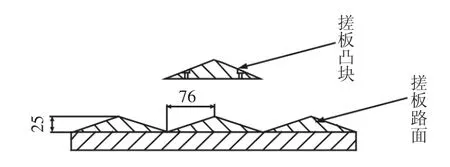
图2 搓板路面与对应凸块Fig.2 The Washboard Road and Corresponding Block
2.1.2 二次项运动规律
二次项运动规律线图,如图3所示。

图3 二次项运动规律线图Fig.3 Quadratic Term Motion Law Diagram
(1)等加速段AB的运动方程式:

(2)等减速段BC的运动方程式:

设两段运动方程式的衔接点上转鼓转角为φ1,边界条件为:

φ=φ 时 s=h。

代入式(3)及式(4)得:
①等加速段的运动方程式为:

其中,φ∈[0,φ1]。
②等减速段的运动方程式为:
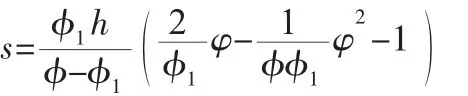
其中,φ∈[φ1,φ]。
2.1.3 简谐运动规律
此处省略推导,直接列出其运动方程式:

其中,φ∈[0,φ]。
在设计凸块轮廓时,上述几种运动规律的下降行程和上升行程轮廓的设计基准相同。令下降行程位移表达式为s′=f(φ′),φ′为下降行程对应的转鼓转角,在下降行程起始位置上φ′=0,则下降行程位移表达式与上升行程位移表达式的关系为s′=h-s。
根据上文所述的多项式类型运动规律及简谐运动规律,各种凹凸形状不同的路面可采取不同的组合型运动规律拟合,使轮廓曲线更加接近于实际路面轮廓形状。
2.2 建立凸块设计的数学模型
建立转鼓—车轮坐标系[3],如图4所示。

图4 凸块轮廓解析法分析Fig.4 Analysis of the Block Contour
(1)凸块轮廓的直角坐标方程

式中:φ—转鼓转角;s—车轮中心位移;e—车轮相对转鼓的偏距;

(2)凸块轮廓直角坐标的一阶和二阶导函数是:

根据路面信息得到车轮的运动规律s=f(φ),推导出对应的一阶导函数d s/dφ和二阶导函数d2s/dφ2,然后利用MATLAB进行解析计算,可绘制出凸块的轮廓线图及车轮的速度—转鼓转角线图、车轮的加速度—转鼓转角线图。
3 转鼓波浪路面凸块设计
根据某汽车厂试验跑道路面设置要求,如表1所示。以波浪路面的凸块轮廓设计为例。

表 1试验跑道路面设置Tab.1 The Setting of Test Track Pavement
3.1 波浪路面凸块轮廓设计
波浪路面是一种尺寸较大的形状近似为正弦曲线的混泥土路面,波峰(50~100)mm,周期 300mm 以上。
参考某汽车厂试验跑道波浪路面设计,波浪坑按行进方向左右交替铺设,宽度满足车型轮距要求,选用参数为波峰100mm,周期1276.7mm。理论上转鼓的直径越大转鼓表面的曲率越小,转鼓对真实路面的复现程度就越高,综合考虑加工难度和成本等条件,选用的转鼓直径为48英寸(rb=609.6mm)。选用试验车轮半径为rt=353.2mm,根据波浪路面的试验车速换算转鼓转速为n=43.51r/min。
建立波浪路面周期直角坐标系,如图5所示,

图5 波浪路面位移线图Fig.5 The Displacement Diagram of Wave Road
按上述二次项运动规律拟合该波浪路面轮廓曲线,根据路面信息,可知路面最大高度h=100mm,转毂转过一圈为2π,等分后AB段转鼓转角与BC段转鼓转角相等,即φ1=φ2=φ/2。
建立波浪路面运动规律方程:
(1)AB段等加速运动规律

(2)BC段等减速运动规律为:
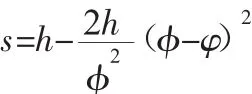
(3)CD段等加速运动规律为:
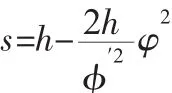
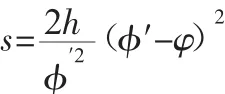
在建立路面模型时,不同的路面需要根据选取的转鼓直径将路面等分为相应的转鼓转角,建立车轮位移与转鼓转角的运动规律方程式。
3.2 MATLAB运算和仿真结果
(1)转鼓转角与凸块轮廓坐标关系,如表2所示。
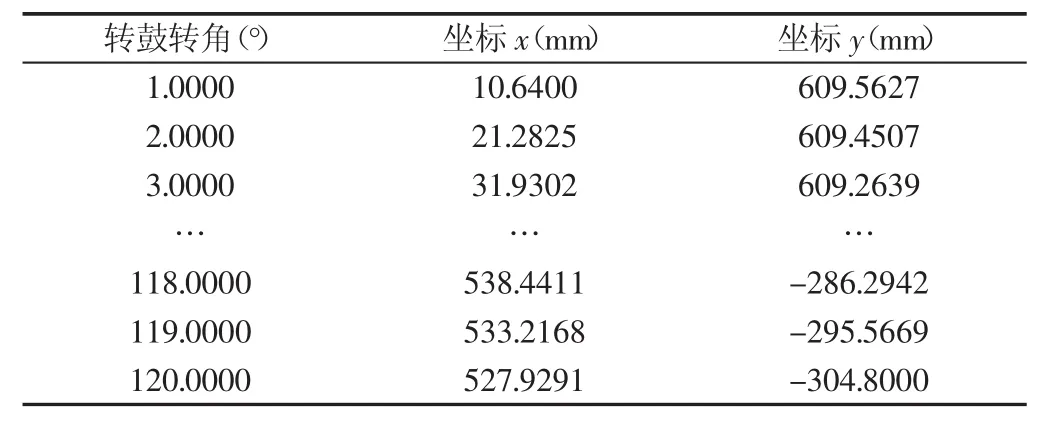
表2 转鼓转角与凸块轮廓坐标关系Tab.2 Drum Angle with the Convex Contour Coordinates
(2)转鼓转角与凸块轮廓向径关系,如表3所示。

表3 转鼓转角与凸块轮廓向径关系Tab.3 Drum Angle with the Diameter of Convex Contour
由上表所得的转鼓转角与凸块轮廓坐标及向径的关系,可绘出波浪路面周期凸块轮廓,如图6所示。
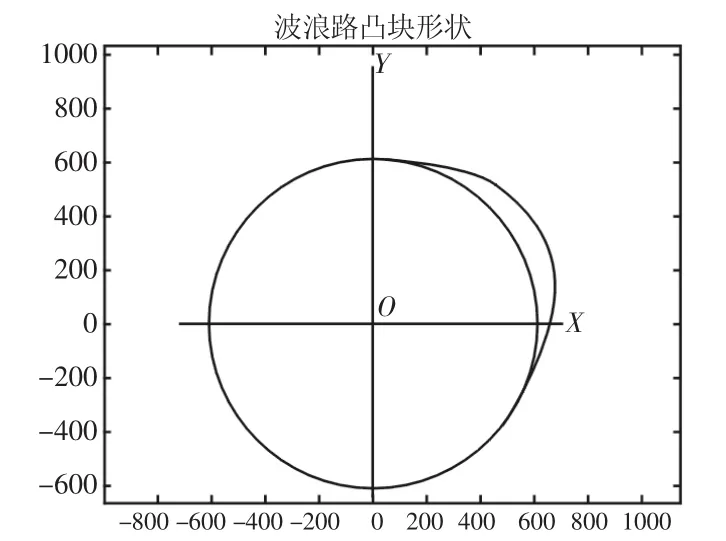
图6 波浪路面周期凸块轮廓Fig.6 The Wave Road Block Contour
采用MATLAB进行转鼓凸块轮廓的设计,可以快速解析不同转鼓直径对应的凸块轮廓。凸块轮廓形状可采用不同的运动规律或组合型运动规律实现,如这里所述的波浪路面轮廓形状可采用简谐运动规律或简谐与二次运动规律的组合形式实现,使形成的凸块轮廓更加接近于实际路面。
3.3 构建虚拟转鼓波浪路面
利用MATLAB设计出的凸块轮廓不仅可以直接用于数控加工凸块,也可以借助动力学仿真软件ADAMS,构建能反映实际路面信息的路面文件,用于整车试验路面模拟的动力学仿真,为仿真结果的准确性建立一定的基础。3D等效容积路面是由一系列有序的空间三角形平面构建的三维路面,对于具有复杂几何特征的转鼓路面的构建,主要使用3D等效容积路面为模板来构建[4]。在构建3D等效容积路面时,ADAMS要求用户在道路参考坐标系中首先指定所有节点的坐标,然后对每个三角形单元指定3个节点和相应的摩擦系数。路面构建过程中最关键的是获得路面的节点和单元,获取节点和单元的方法有很多,可以通过路面数据采集仪采集路面信息,也可以通过编程的手段生成节点和单元信息。此外,由于3D等效容积路面的构建原理与有限元软件中的2D网格类似,也可以借助有限元软件来获得这些节点和单元信息。
借助有限元软件获得转鼓波浪路面的节点、单元信息,首先利用Matlab解析得到的凸块轮廓直角坐标,导入三维软件Catia中构成转鼓波浪路面曲面模型;再将曲面模型导入到有限元软件Hypermesh中进行三角形网格划分,获得路面的节点和单元参数,再将数据导出到Excel中编辑;最后以Adams提供的3D等效凹凸路面为模板,替换其中的节点和单元信息,修改其中的节点和单元数量以及摩擦系数,生成转鼓波浪3D路面,该路面文件可为整车的动力学仿真分析提供较为准确的转鼓路面信息。通过此种方法可以构建多种虚拟的3D转鼓路面,其流程,如图7所示。

图7 转鼓鼓面节点和单元信息的获取Fig.7 The Construction Principle of 3D Equivalent Volume Pavement
3.4 波浪路面凸块的加工安装
为了将凸块安装在转鼓上,凸块需要有基础厚度,即t=0时凸块的厚度,基础厚度大小应合适,以节省材料、减轻重量,因此凸块安装板选择基础厚度为30mm。凸块也有不同的制造方法,综合考虑加工难度和成本,按不同的加工方式凸块组分为两类:一种是浇筑式凸块,另一种是机加工式凸块。浇筑式凸块,即根据转鼓周长将模拟路面均分成若干块并分别浇筑成块。根据试验所需的不同等级的路面浇筑不同表面粗糙度的试验路面,再将浇筑好的水泥或者沥青路面块通过安装框拼装在转鼓表面。机械加工式凸块是根据不同的试验路面突起的几何形状,加工出类似形状的凸块,凸块带有安装孔,可根据实际路面中的凸块之间空间几何关系,将路面分散为不同的凸块来加工,凸块与转毂之间以内六角螺钉与转毂支座上的螺纹孔连接,凸块采用沉头孔设计,方便拆卸,材料可以选用尼龙、铝合金等质地较硬、耐磨的材料[5]。转鼓波浪路面属于几何形状不复杂的路面凸块,考虑到成本和便捷性等因素,可以采用机加工方式获取。转鼓波浪路面对应的凸块简图,如图8所示。波浪凸块布置于转鼓上时,可将两个转鼓左右两侧的波浪凸块错位布置,造成左右车轮相位差,形成的激励类似于扭曲路面,使试验车辆产生强烈的扭曲,用于检验车辆的车架、车身结构刚度和各系统的连接强度、干涉等。

图8 转鼓波浪路面对应凸块Fig.8 The Wave Road and Corresponding Block
4 结束语
(1)转鼓试验台路面模拟方法包括:建立路面轮廓模型;以Matlab为平台采用解析法设计凸块轮廓;用有限元方法构建3D路面的凸块轮廓等;该过程形成的3D路面既可以用于构建汽车动力学分析过程需要的虚拟路面,也可以用于凸块轮廓加工的数控加工文件,为转鼓试验台路面模拟的实际工程应用奠定了基础。
(2)通过在两转鼓上加装各种形式的凸块不仅可以模拟多种路面,还可以通过交错分布左右两侧转鼓凸块,实现同轴两轮同向或异向激励,实现多种运行工况的路面模拟试验。因此,转鼓试验台特别适用于整车性能试验,特别是可靠性或耐久性试验。
(3)进行了转鼓试验台路面模拟的凸块轮廓设计,说明任何轮廓形状的路面都可以通过配置形状各异的凸块实现模拟,凸块的轮廓形状可以采用典型运动规律的组合而实现。按此种方法,可以设计多种典型路面凸块,如搓衣板路面、减速带路面、扭曲路面等,具有方便、直观、准确的优点。

