利用数据挖掘方法探索流域尺度气象干旱预报的研究

措 姆，加勇次成，红 梅

(1. 西藏山南市气象局，西藏 山南 856000；2. 拉萨市自治区气象局， 拉萨 850000)

1 前 言

西藏地区的气候主要以频繁和严重的干旱事件为特征[1]。干旱的气候导致生态系统十分脆弱，特别是在生态系统极其脆弱的干旱、半干旱区，草场退化、土地沙化等生态问题随着干旱气候的加剧而日益显著，资源环境健康与社会发展之间的矛盾也由此而日趋凸显，严重影响着当地农牧民生产生活水平。因此在干旱气候准确预测的基础上科学进行水资源的调配和管理对提高藏区生态环境具有重要意义。

已有的大量研究表明时空气候相关分析和数值模拟被认为是适合气象干旱预测的方法[2～4]。文献[5]研究了利用北大西洋涛动和厄尔尼诺遥相关预测西藏不同地区降水和径流的可能性。文献[6]使用基于回归的支持向量机(SVM)和基于过滤器的特征选择方法来预测位于西藏北部的集水区的标准化降水指数(SPI)。该研究指出季节性干旱指数可以通过提前几个月提出的程序进行预测，并且适用于水资源管理决策过程。文献[7]将人工智能、数据挖掘和统计学习方法应用于预测SPI，并将SPI归类为量化气象干旱严重程度的最主要指标之一。

在制定干旱预报模型时，其中一个重要步骤是特征选择，通过这些特征选择筛选诸如各种气象变量的候选预测因子，以找出最有影响力的组合。文献[8]使用平均互信息(AMI)指数作为基于过滤器的特征选择方法来识别和选择降水，海表温度异常模式，输出长波辐射的时间和空间梯度的空间数据集中的最佳输入变量集合(预测变量)，风应力异常。

本文的目的是评估优化支持向量机(SVM)和数据处理分组方法(GMDH)作为常用的数据挖掘方法在识别气象变量变化中的重复统计模式时的性能。为了实现SVM模型的最佳性能，使用粒子群优化(PSO)算法来校准模型参数。而数据处理的分组方法(GMDH)是在水资源和水文学研究中应用较为普遍的基于自组织多项式的数据挖掘方法。本文通过怒江流域所采集的降水数据集对两种预测模型的性能对比，以发现两种数据挖掘方法在流域尺度上对气象干旱的类型的识别能力。

2 干旱和标准降水指数

SPI用以评估气象干旱的严重程度和降水量不足[9]。SPI值在-3～+3之间，其正值(或负值)表示比中值降水大(或更少)。作为与中值差异的衡量指标，SPI是基于过去记录的降水量的湿度或干旱严重程度的概率指示。用于模拟降水数据概率分布的伽马分布为：

(1)

在计算SPI时，伽马分布被转化为高斯分布。然后计算标准化异常，结果为零均值，标准偏差为1。经过上述计算步骤使得SPI不受地理位置和取值范围的影响，使不同的季节和气候区域以相等的基础来表示。基于SPI值把干旱划分为7个类别，如表1所示。

SPI旨在量化多个时间尺度下的降水量不足。 这些时间尺度反映了气象干旱对水资源可用性的影响。土壤湿度条件在相对较短的时间尺度上对降水异常作出反应。地下水和水库的储量变化会对长期降水异常产生响应。在本文的研究中，计算SPI时考虑3、6和9个月的时间尺度。

表1 基于SPI的干旱类别划分Tab.1 Classification of drought types based on SPI

3 数据挖掘相关技术

3.1 支持向量机(SVM)

支持向量机是众所周知的一种统计学习方法，旨在识别数据结构。检测数据结构时，SVM的特征之一是使用核函数将原始数据从输入空间转换到新空间(特征空间)[10～12]。为此，定义了非线性变换函数φ(·)，以将输入空间映射到更高维的特征空间。f(·)的输入(xi)和输出(yi)之间的非线性关系如下所示：

yi=f(xi)=w,φ(xi)+b

(2)

式(2)中w和b是模型参数。SVM可以用于回归和分类。在本文中，SVR用于通过找到以下原始问题的最优解来预测季节SPI值：

(3)

式3的约束条件为：

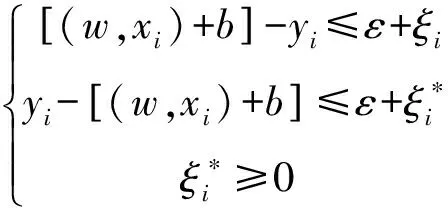
式(3)中，L表示训练数据集中的数据点数，C为SVM模型参数，xi为特征空间的数据点，w表示问题的优化解决方案，模型残值ξ=yi-f(xi)。

表2 核函数及其对应参数Tab.2 Kernel functions and their corresponding parameters

支持向量机参数必须经过校准和优化。已经提出了不同的方法来实现最佳的模型性能。在本研究中，LIBSVM工具箱用于SVM建模。粒子群优化(PSO)被用来校准SVM参数[14]。

3.2 数据处理的分组方法(GMDH)

数据处理的分组方法是一种统计非线性多变量分析，可用于检测复杂系统中输入输出关系的复杂结构。数据处理的分组方法基于嵌套二次或三次多项式的分化能力来模拟回归和分类主题[15]。数据处理的分组方法结构层的一般多项式形式如下所示：

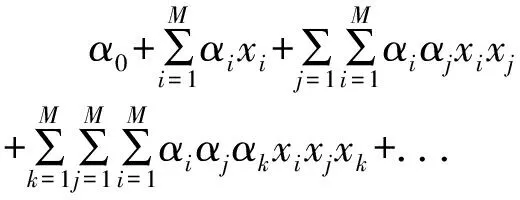
(4)

式(4)中，xi(i=1,...M)是第ith个输入变量， 是可用输入的数量，M是权重。使用简单的最小二乘法来计算模型参数，同时最小化输出层和观测值之间的残差。通常，多项式集的阶数等于二或三。

三层数据处理的分组模型的示意嵌套结构如图1所示。

图1中，数据处理分组方法中每层由许多节点组成，作为其传递函数(多项式)的输入，而传递函数的计算结果传递到下一层传递函数，如此反复。在每一层中，选择适当数量的变量，并考虑在该层中传递函数的结果。数据处理分组模型结构的组织方式是，在考虑不同条件(例如最大层数或实现特定的错误阈值或模型性能)的情况下，实现计算和观察值之间的最小剩余。

3.3 粒子群优化(PSO)

PSO会生成一个随机的解决方案，在这个算法中被称为粒子。每个粒子在决策空间中都表现出一个点。每个粒子访问的最佳位置称为局部最佳。所有粒子的最佳位置称为全局最佳。每个粒子使用以下公式搜索全部最佳和全局最佳：

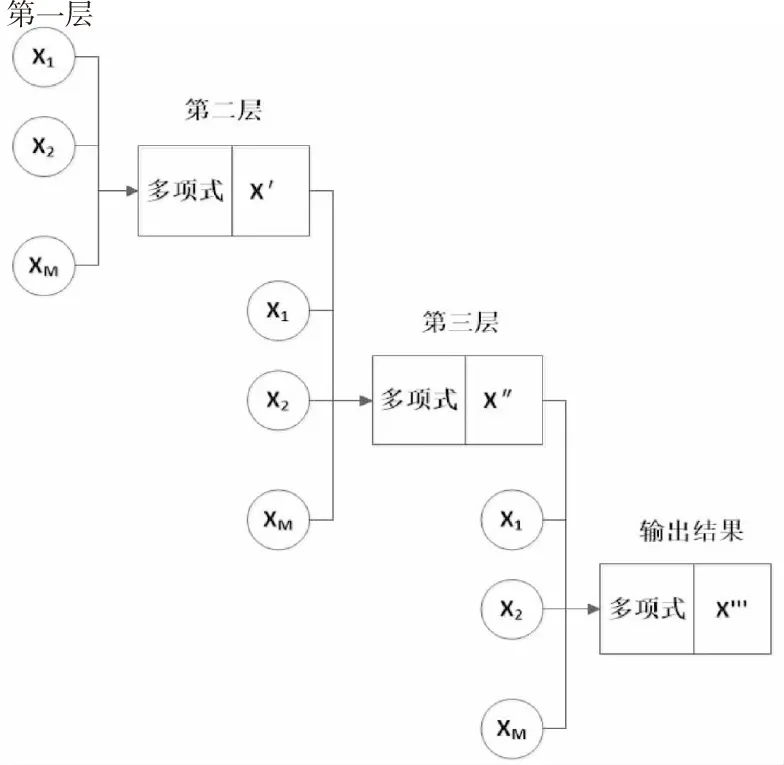
图1 数据处理的分组方法Fig.1 Data processing grouping method

(5)

(6)

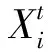
3.4 基于过滤器的特征选择

特征选择过程可被认为是机器学习中全局组合优化中具有挑战性的一步。正确的特征选择减少了特征的数量，消除了不相关的、噪声和冗余的数据，并获得了可接受的分类准确度。特征选择方法中通常使用基于过滤器的技术来实现特征识别和选择。过滤技术基于输出变量对输入候选的依赖性的统计度量来执行，作为特征(或输入)选择的构建块。线性相关系数是特征选择最常用的统计标准之一。本文将统计过滤器(AMI)应用于在水资源建模问题中。在多维模型开发过程中，AMI是一种更合适的特征选择统计度量，因为它没有对变量的依赖结构进行任何额外的假设。基于两个离散随机变量x和y的统计过滤器定义为：

(7)

式(7)中p(x,y)是x和y的联合概率分布函数，p1(x)和p2(x)分别是x和y的边际概率分布函数。在连续的情况下，式7将被以下定义的二重积分代替：

(8)

4 建模方法

针对流域尺度的区域气象干旱预测的建模过程如图2所示。

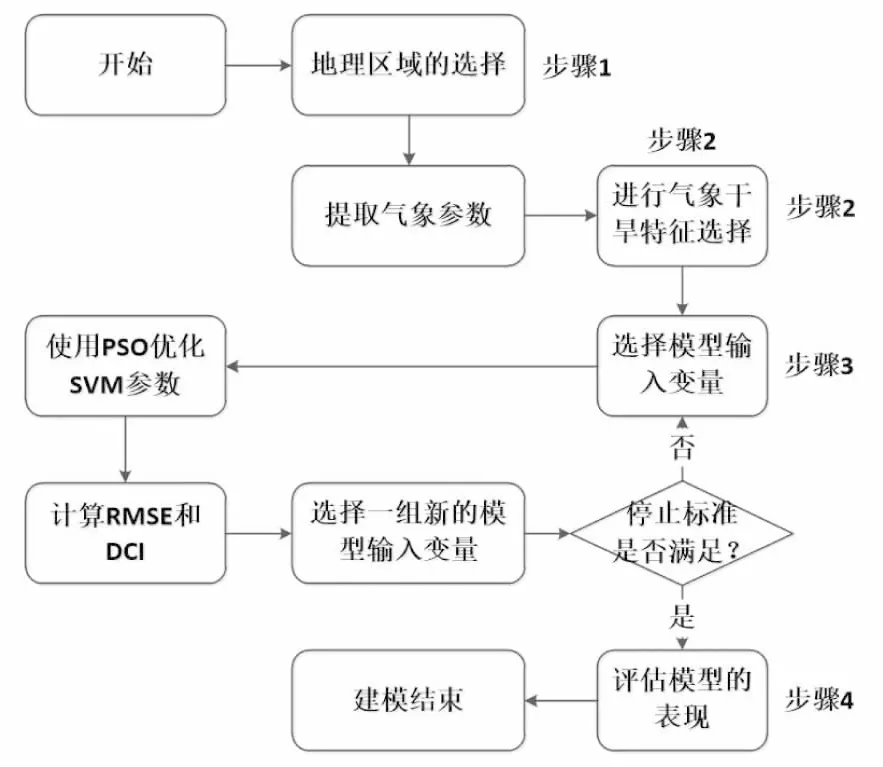
图2 SVM的SPI预测流程图Fig.2 SPI Predictive Flowchart of SVM

4.1 预测因子的选择

图2中步骤1的目的是选择预测因子所在的地理区域。在本文中，预测因子是3、6、9个月的平均SPI。应选择SPI值预测的季节，以便它们可以用于水资源规划和管理决策过程。预测因子的选择应该为水资源管理者和决策者创造足够的预测时间，从而从模型预测中受益。

4.2 特征选择

由于月份、气象变量和地理区域的不同组合使得候选预测因子的数量增加，使用特征选择方法至关重要。特征选择为图2中的步骤2。该过程可能因地区而异。应选择特定地点的研究来选择预测因子。在本文中，AMI指数被用作特征选择过滤器来选择提供最佳预测准确度的预测因子的合适子集。必须指出，SVM和GMDH建模技术都只能解释预测和预测之间的统计关系，但无法解释所选组合的物理基础。

4.3 SPI估算

由于本研究的主要目的是预测影响研究区域的气象干旱严重程度，因此步骤1中所选季节的3、6和9个月平均SPI值使用区域平均降水量来预测的。所实现的的反距离加权基于这样的假设：内插表面应该主要受附近点影响，而较少受到较远点影响。然后使用式1将每个区域平均降水量值转换为SPI。

4.4 预测模型的训练和验证

可用数据集被划分为训练、验证和测试子集。在本文中，50%的可用数据被选中进行模型训练。选定的预测变量在建模之前已经标准化。当使用数据挖掘方法来减少数据集的系统偏差时，标准化被广泛用作预处理步骤。在训练阶段，评估不同的核心功能，对核心的SVM参数C和ε进行校准，并使用均方误差(MSE)来评估训练过程的准确性。完成训练后对模型进行验证，使用20%的可用数据集用于重新生成SPI值并评估经过训练模型的性能，其余30%数据用于测试模型性能。经过不同的模拟，选择径向基函数(RBF)核函数将数据集投影到一个新的空间。寻找最佳模型预测因子和估计优化SVR模型的参数如图2中的步骤3所示。当使用GMDH进行SPI预测时，图2中的步骤3必须改变，因为GMDH模型是自组织模型并自动选择预测变量和参数。

5 仿真评估

研究区域为自西北横穿西藏的怒江流域。怒江流域中国境内干流长约2 013km，流域面积13.6km2。本研究选取发布在怒江流域中上游的那曲、昌都、贡山和泸水四个气象站的所属43个降水观测点的2015～2016年月度降水观测数据作为研究数据集(见表3)。采用优化的反距离加权(IDW)方法处理雨量观测时间序列并用于估算流域的面积降水量。首先根据式(1)，将月平均降水量的时间序列转化为SPI时间序列。

为了评估预测模型结果的准确性，不仅SPI的预测值的估计误差很重要，而且还必须考虑表1中解释的预测正确的气象干旱等级的准确性。在本研究中使用均方根误差(RMSE)作为前者和干旱兼容性指数(DCI)的指标，作为后者的指标。RMSE和DCI分别被用作相异性和相似性指标。RMSE和DCI使用以下公式进行计算：

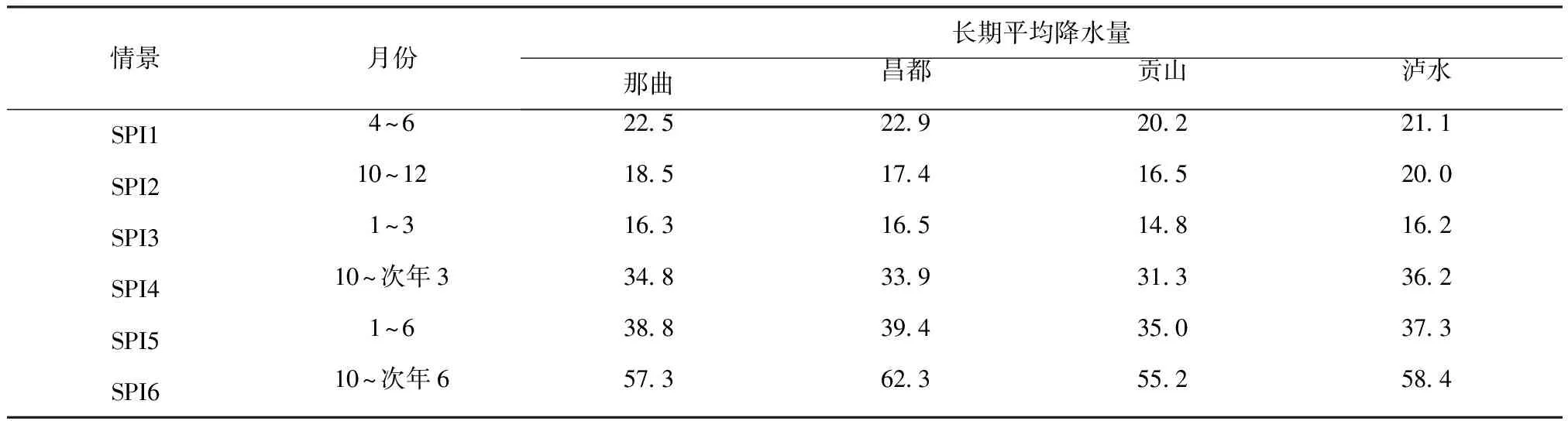
表3 四个气象观测站区域的干旱情景和长期平均降水量Tab.3 Drought scenarios and long-term average precipitation in the four meteorological observatory areas (cm)

(9)

式(9)中Xp是预测的SPI，Xo是观测到的SPI，n是数据点的个数。应该指出的是，预测的准确性通常与预测的前置时间相关。准备时间越长，准确度相对更低，但对指导多季节水资源规划决策过程而言，这些预测数据可能更有用。

使用优化的SVM在训练、验证和评估数据集中预测和观测SPI结果。统计结果如表4所示。

表4 SVM的仿真结果Tab.4 SVM simulation results

由表4的可以看出，SPI4-贡山、SPI1-贡山、SPI6-昌都、SPI2-那曲和SPI1-昌都区域的预测数据分别获得了基于RMSE的最佳模型验证结果。该表中的RMSE结果还表明，训练和测试数据集中模型的性能比训练和验证数据集的模型性能更接近。因此，可以得出结论：没有发生过度拟合。SPI3-泸水和SPI4-贡山区域的仿真结果分别出现了训练和验证数据集中RMSE和DCI指数之间的最大差异。

使用GMDH在训练、验证和评估数据集中预测和观测SPI结果。统计结果如表5所示。

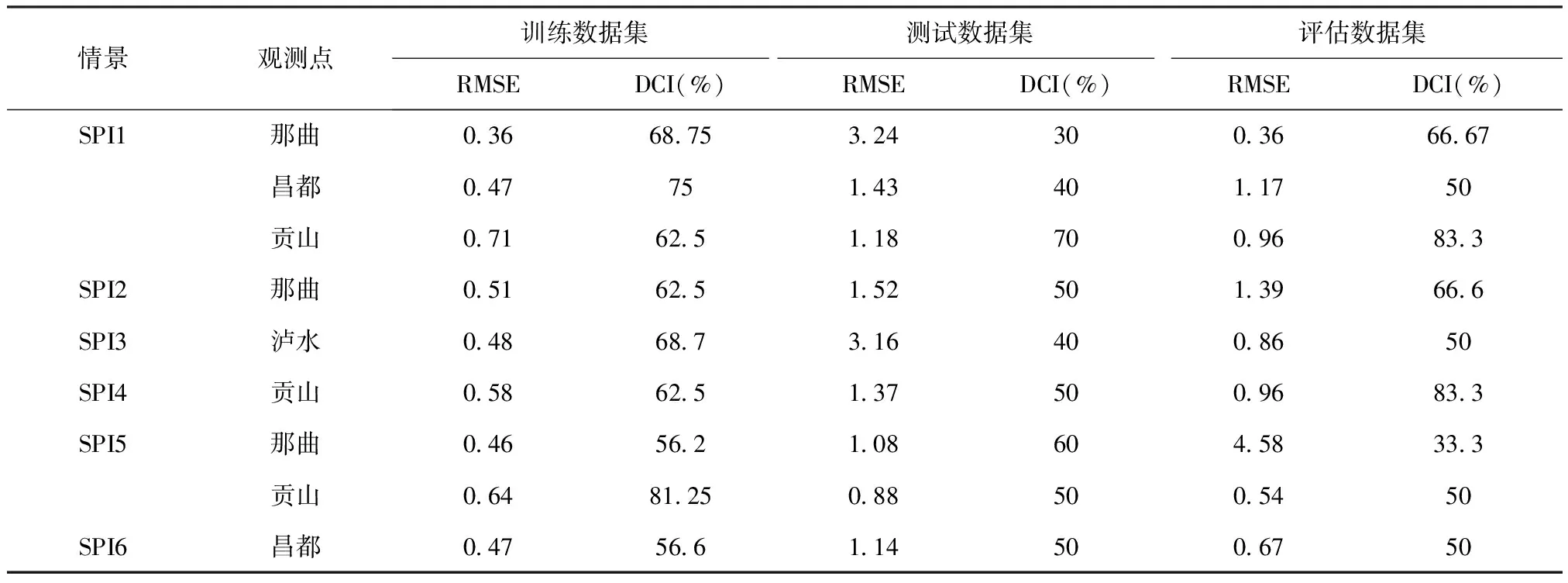
表5 GMDH的仿真结果Tab.5 GMDH simulation results

在表5中，列出了GMDH仿真结果与观测值的统计相似性和不相似性。

SVM和GMDH模型的结果比较表明，在训练模式下SVM优于GMDH，但验证和测试数据集的结果并没有显示出明显的差异。

SVM预测准确度比GMDH的要好的主要原因是由于GMDH对传递函数的多项式阶数敏感。此外GMDH效率与优化后的SVR差异的主要原因可能与GMDH序贯自组织特性的有效性以及优化方法(PSO)在校准SVM参数中的应用有关。

6 结 论

本文分别采用SVM和GMDH方法对对流域尺度的气象干旱进行建模，并通过怒江流域的气象数据集进行模型仿真。通过实验表明，GMDH模型作为一种具有自组织特性的神经网络，其预测结果比SVM模型更稳定，而SVM模型的预测准确度更好。本文的研究表明，气象预测模型的选择可以显著影响预测结果的准确性和稳定度，因此下一步的研究重点是对现有模型进行优化，以期获得更加优异的气象干旱预报的准确度。