两端固支屈曲梁准零刚度隔振器的微振动隔振性能分析

王云峰， 李 博， 王利桐

(天津航天机电设备研究所 天津市微低重力环境模拟技术重点实验室，天津 300458)

航天器微振动通常是指在空间微低重力环境下由航天器上活动部件工作产生的一种幅值较低(微米级)、带宽位于1～1 kHz的振动或扰动[1]。产生微振动的活动部件有控制力矩陀螺(Control Moment Gyro, CMG)、太阳翼驱动机构(Solar Array Drive Assembly Mechanism, SADAM)以及动量轮(Momentum Wheel Assembly, MWA)等[2]，由于空间环境阻尼较小，整星抖动会长时间持续存在，影响相机等高精度敏感设备正常工作。因此，减少微振动向相机有效载荷的传递，对提高相机成像质量具有重要意义。

准零刚度系统一般是通过正刚度和负刚度系统并联来实现，典型的准零刚度系统结构型式是使用线性竖向弹簧和斜向弹簧并联[5-9]，其他实现准零刚度的途径还有：利用空气弹簧[10]、碟形弹簧[11]、凸轮-弹簧机构[12]、电磁铁[13]、欧拉屈曲梁等。其中欧拉屈曲梁准零刚度系统通过使用欧拉屈曲梁提供负刚度，与正刚度弹簧并联，具有较好的低频隔振性能。

文献[14]中屈曲梁两端通过铰接与负载和基座相连，由于铰接中存在间隙，不利于微振动隔振[15]，Platus[16]利用两端固支屈曲梁建立竖向准零刚度隔振系统，有效避免铰接间隙的影响，但未对固支屈曲梁结构参数对隔振性能的影响展开深入分析。Benjamin等[17]将两端固支屈曲梁准零刚度隔振器用于振动和冲击隔离研究，取得明显的隔振和隔冲效果，但文中屈曲梁负刚度中忽略了高阶项的影响，并且未从理论上对系统的整体动力学特性进行分析。

本文以微振动隔振为目标，研究使用两端固支屈曲梁准零刚度隔振系统进行微振动隔振，首先分析两端固支屈曲梁负刚度的产生机理，其次，通过理论计算，分析屈曲梁和线性弹簧并联的准零刚度特性，考虑不同阻尼和扰动幅值系统传递率的影响，最后，通过仿真对系统的隔振性能进行了验证。

1 两端固支屈曲梁负刚度模型

预压梁结构屈曲形式包括线性屈曲和非线性屈曲两种，在横向大位移、大变形条件下，梁结构在两个稳态之间跳转会发生非线性屈曲，表现出复杂的动力学行为[18]。在横向小位移条件下，梁结构在两个稳态之间的跳转可近似为一阶模态屈曲，在横向力作用下，屈曲梁的跳转过程如图1所示。

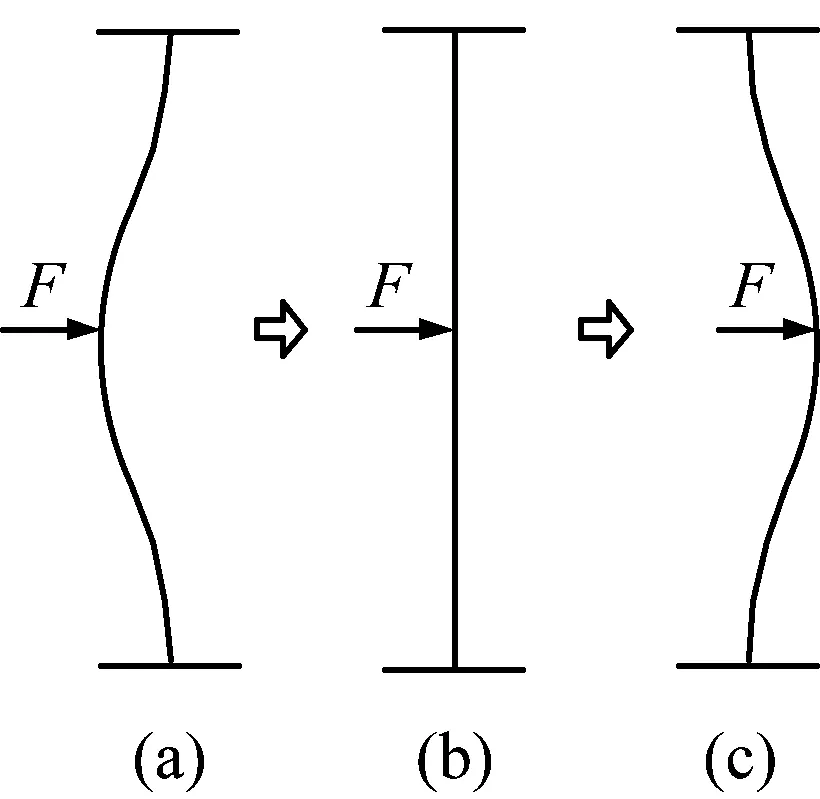
图1 横向力作用下屈曲梁一阶模态跳转

如图2所示，为得到屈曲梁的负刚度模型，令两端固支梁的右固定端从位置a移到位置b，在轴向产生预紧力P，在x方向产生位移ux。在梁中点处施加一个y向力F，中心位置在y向产生位移uy。

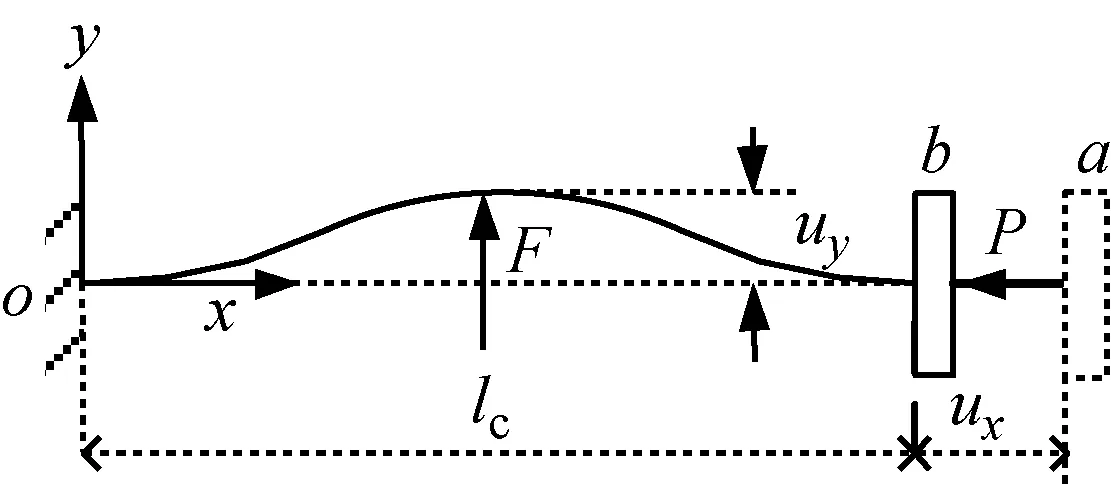
图2 预压屈曲梁受力简图

变形后梁的挠曲线满足两端固支梁的一阶模态振型

(1)

则屈曲梁挠曲线的长为[19]

(2)

令梁原长为l0，即l0=lc+ux，则梁轴向压缩产生的势能为

(3)

梁弯曲变形产生的势能为

(4)

梁变形产生的全部势能与施加的力F之间满足

(5)

得到系统刚度为

(6)

梁的轴向刚度为

(7)

(8)

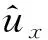
(9)

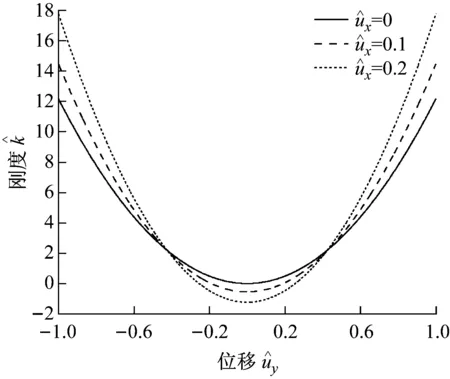
图3 不同值对应屈曲梁刚度值曲线

在竖向并联一个刚度为k1的线性弹簧后，如图4所示，竖向力与梁中点位移变为

(10)

对uy求导并无量纲化处理后，得到刚度为

(11)

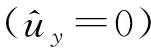
(12)

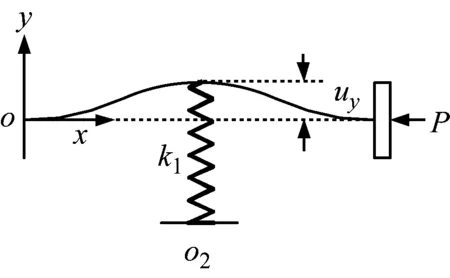
图4 屈曲梁-弹簧系统结构图

2 屈曲梁准零刚度系统动力学模型

为实现超低频隔振的目的，将屈曲梁负刚度系统与具有正刚度的线性弹簧并联，构建准零刚度隔振系统，其结构原理图如图6所示。

图6中，线性弹簧刚度为k，系统阻尼系数为c，基础产生的位移激励为uh，质量为m的负载产生的位移为uy，令y=uy-uh为负载相对基础的位移，其中，uh=Hsin(ωt)，利用拉格朗日方法建立系统的动力学模型。

线性弹簧的压缩势能为

(13)

质量块的动能为

(14)

得到拉格朗日函数

L=T-Uc-Ub-Uk

(15)

计算得到无量纲化的系统动力学模型为

(16)

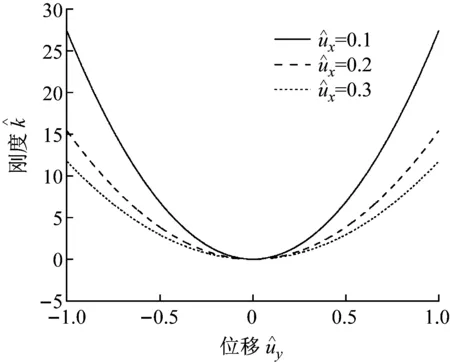
(a) 不同值对应屈曲梁-线性弹簧刚度值曲线

(b)不同值对应屈曲梁-线性弹簧刚度值曲线

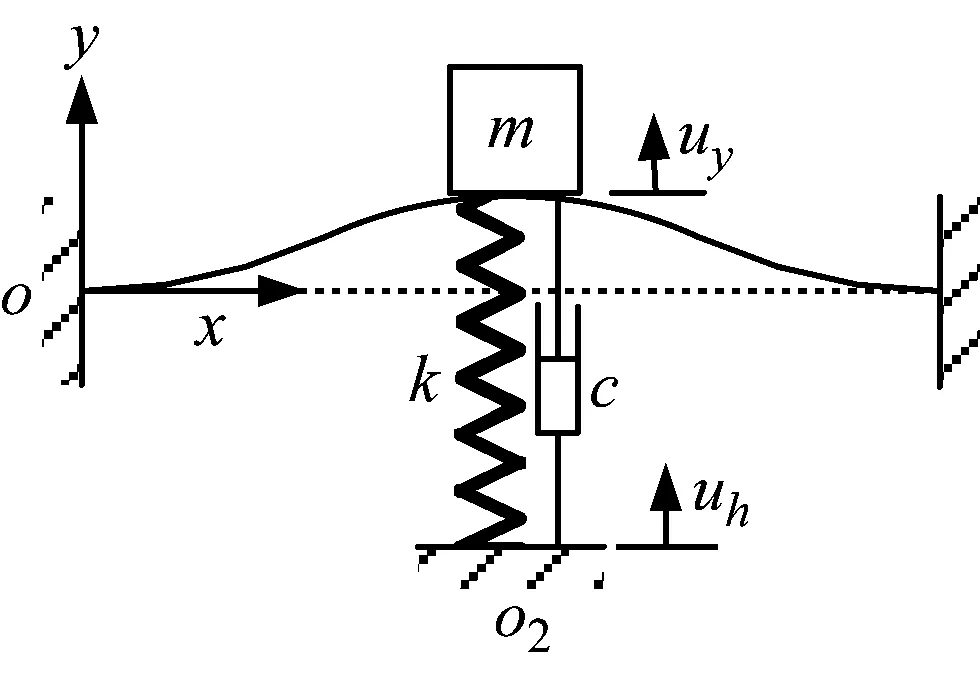
图6 屈曲梁-弹簧准零刚度隔振系统

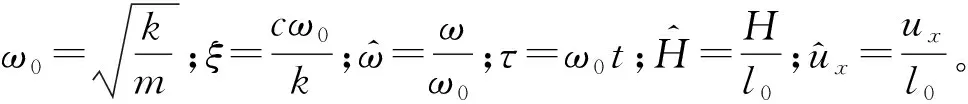
利用谐波平衡法求解系统的响应，假设式(16)的解为

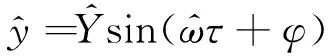
(17)

将式(17)代入式(16)中，并令方程两边的谐波项系数相等，可得

(18)

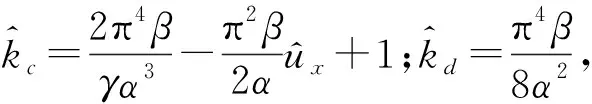
(19)

(20)

由式(19)计算得到响应幅值后，利用式(18)可求得系统绝对位移传递率为

(21)

(22)

则系统响应有界必须满足

(23)

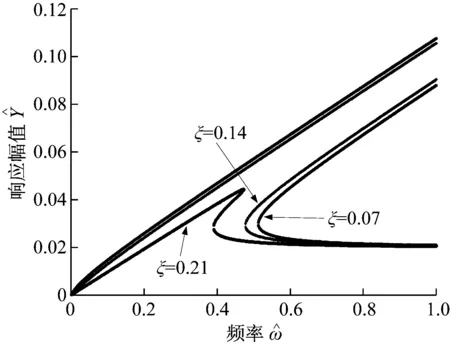
图7 不同阻尼下系统响应

当阻尼大于临界阻尼时，令ξ分别取0.203，0.208，0.211和0.206，得到位移传递率如图8所示。可见阻尼比ξ=0.203时传递率曲线较大程度上向右弯曲，表明响应衰减效果较差，系统不稳定区间较大，对系统隔振不利；随着阻尼比的增加，传递率曲线的共振峰明显减小，同时向下跳跃频率左移，减小了系统的不稳定区间，ξ=0.216时传递率曲线的不稳定区间消失，传递率的共振峰值进一步降低。可见，适度增加阻尼比对改善系统不稳定区间和降低传递率峰值具有积极的作用。

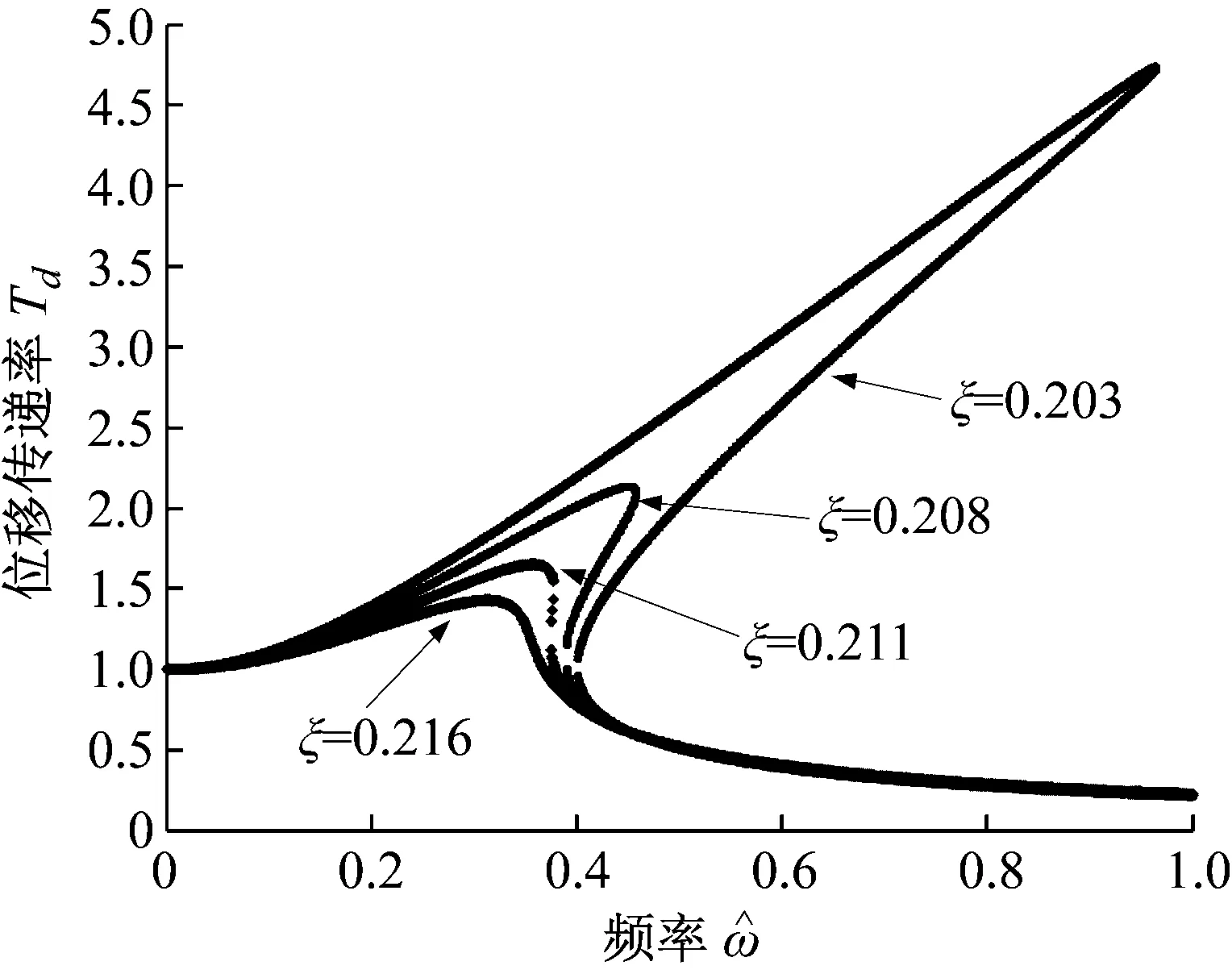
图8 不同阻尼对应的位移传递率

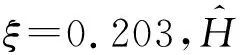
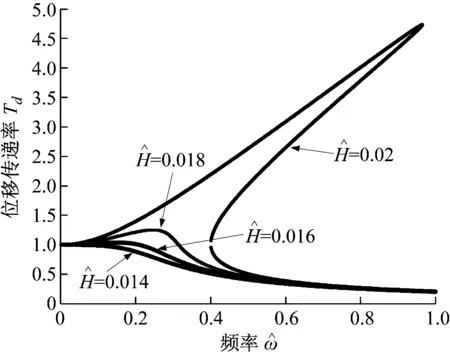
图9 不同激励幅值对应的位移传递率

3 隔振系统仿真

在前文屈曲梁隔振准零刚度系统性能分析的基础上，为综合验证系统的隔振能力，在SIMULINK环境下对该系统进行仿真。仿真模型中参数设置如表1所示。

表1 仿真模型参数

SIMULINK模型结构如图10所示。为得到基础扰动的正弦扫频信号，在Matlab工作空间中生成0～10 Hz幅值为0.5 mm的正弦扫频信号，并对其求微分，得到的的数据被模型中Input_vel模块从工作空间导入用作地基速度扰动信号，在模型中积分后即为基础的位移扰动。其中设置采样间隔0.01 s，采样时间为500 s。

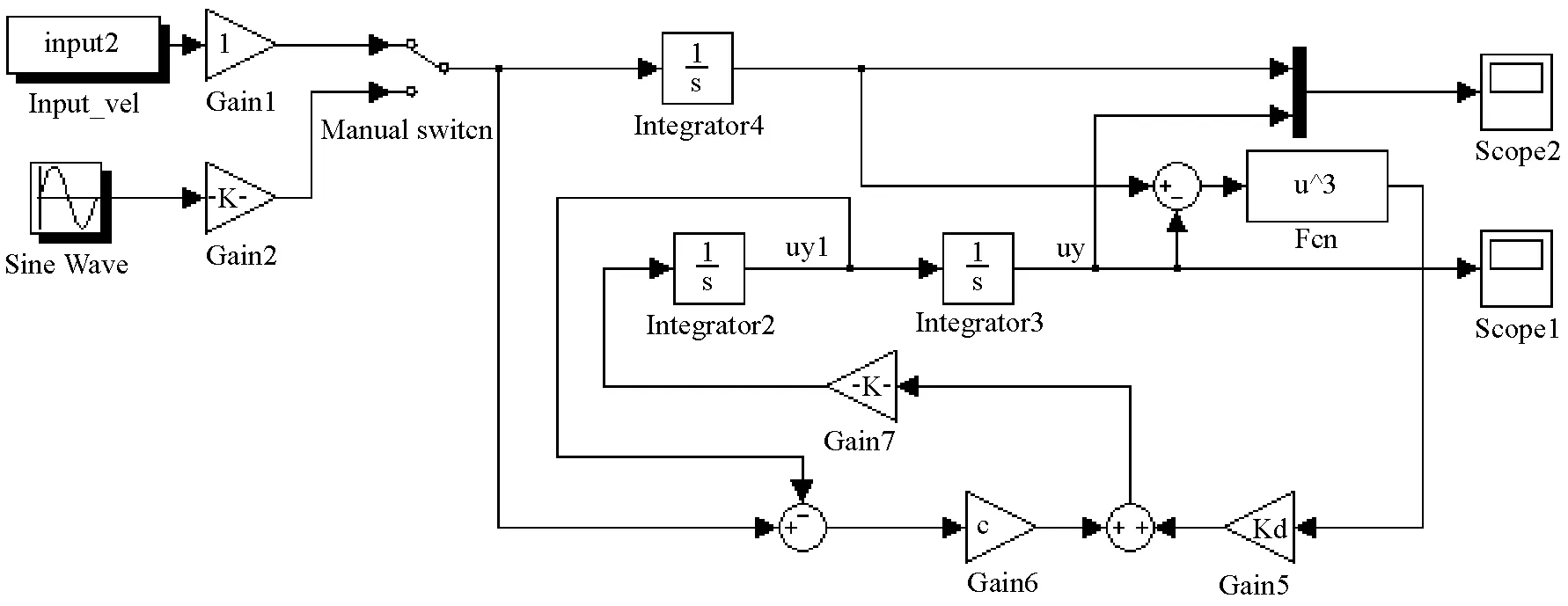
图10 SIMULINK仿真模型

仿真得到的基础扰动与负载位移响应，取前100 s数据对比如图11(a)所示，可见在扫频起始阶段响应信号有较大的幅值，随频率的增加响应的幅值逐渐减小，隔振效果明显。

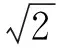
由仿真结果可知，屈曲梁准零刚度隔振系统对扰动具有明显的抑制作用，与线性系统相比尤其对低频、超低频的扰动具有良好的隔振效果。

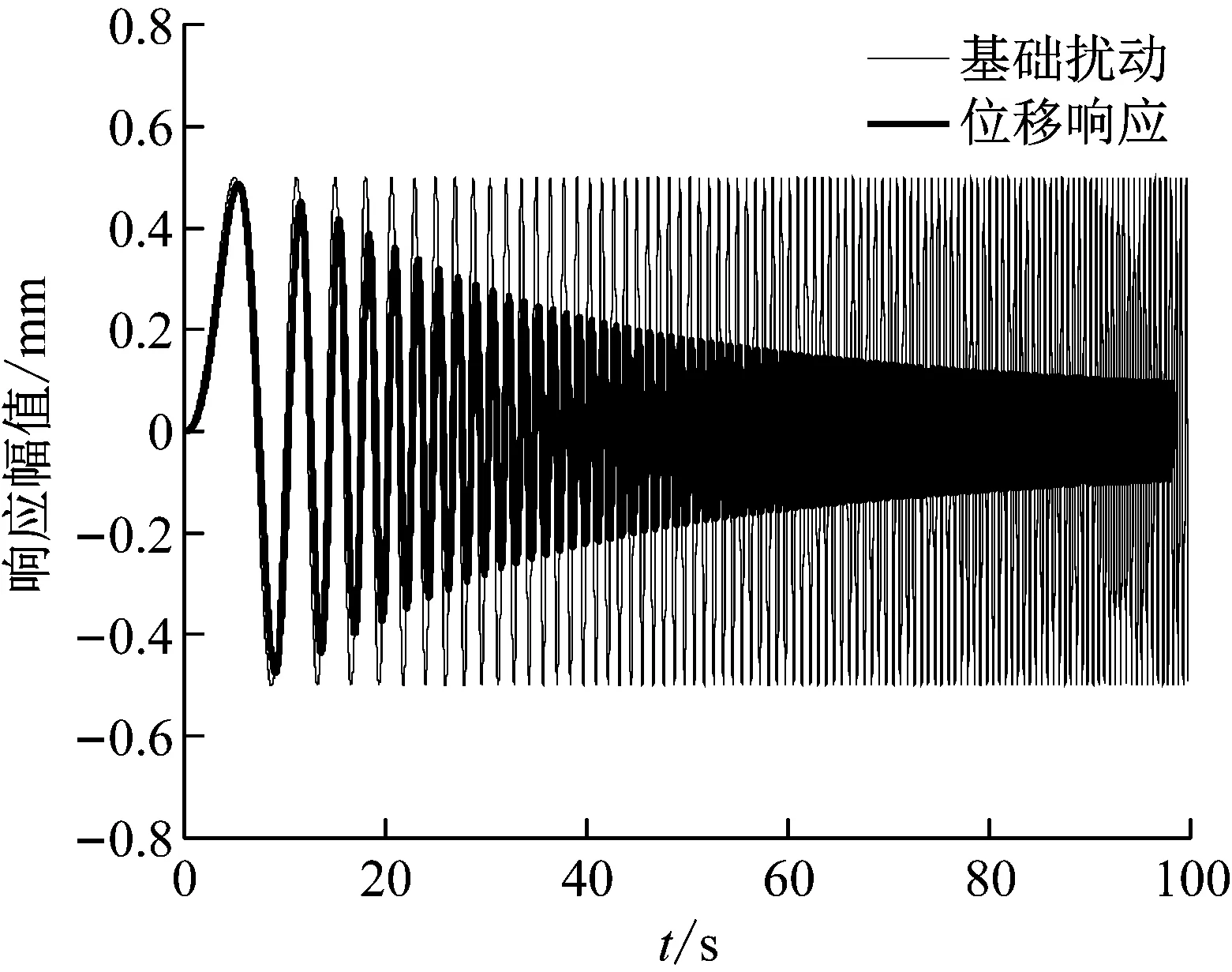
(a) 时域响应-扰动对比

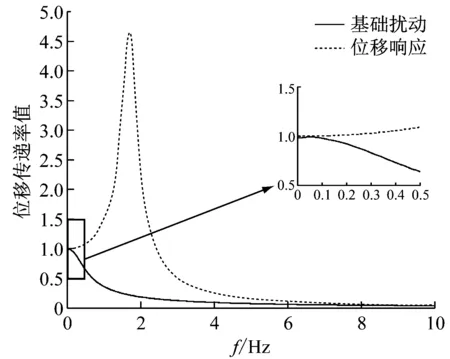
(b) 线性系统与准零刚度系统传递率曲线对比

4 结 论

本文以星上微振动隔离为目标，分析了两端固支屈曲梁准零刚度隔振系统的动力学特性。推导得出了屈曲梁系统的负刚度产生机理，得到了屈曲梁正负刚度并联系统在静平衡位置的零刚度条件，并利用谐波平衡法得到两端固支屈曲梁准零刚度隔振系统的位移响应、传递率与扰动频率之间的关系，最后通过仿真对隔振系统的性能进行了验证。结果表明，在高频段两种隔振系统都能够得到较好的隔振效果；在线性系统固有频率位置，线性隔振系统出现位移放大(传递率大于1)，而准零刚度隔振系统在此位置隔振效率达到-30 dB；在低频和超低频段，屈曲梁准零刚度系统的隔振性能明显优于线性系统。

本文对两端固支屈曲梁隔振器进行了理论和仿真分析，在此基础上，接下来的工作需要通过实验对其动力学特征和隔振性能作进一步分析和验证，以推进其工程应用。