齿轮箱故障非线性特征测度及状态TWSVM辨识研究
曾 柯, 柏 林
(重庆大学 机械传动国家重点实验室,重庆 400044)
齿轮箱振动信号由于系统本身的复杂性,以及振动在传输过程中的衰减和耦合等,往往表现出非线性的特征。尤其是在发生故障时,故障源产生的激励会使齿轮啮合刚度产生相应的变化,这种故障引起的时变刚度使得齿轮振动的非线性和非平稳性更加突出。另者,由于加工和安装引起的误差激励以及非稳态齿轮啮合也会使得齿轮振动本身具有很强的非线性[1]。传统线性和平稳的特征提取技术,容易丢失重要的非线性状态信息,不能很好地从复杂的非线性信号中提取真实反映其非线性振动本质的有效状态特征[2]。因此采用非线性特征测度方法对齿轮箱振动信号进行状态分析,能够更加准确地辨识出齿轮箱的状态特征。
在传统的模式识别方法中,SVM(Support Vector Machine)是一个二分类算法,对均衡或近似均衡分布的样本,分类效果显著[3]。但是对于一个多分类问题,SVM只能通过一对其余或二叉树等多分类方法来实现,但是这些多分类方法都不能解决样本不均衡而导致分类精度降低的问题,SVM在处理该类问题时往往不尽人意[4]。所谓样本不均衡一般是指用于训练分类器的两类样本中,一类样本的数量要远大于另一类[5],样本不均衡问题一般在多分类问题中会经常出现。Jayadeva等[6]提出的TWSVM(Twin Support Vector Machine)可以通过参数的调整克服样本不平衡问题[7]。具体来说TWSVM算法可以通过实施不同的惩罚因子以克服传统SVM处理样本非均衡问题的局限性[8],另外TWSVM其核心思想是构造两个非平行的超平面,并使正类样本靠近正类超平面而负类样本尽可能地远离,使负类样本靠近负类超平面而正类样本尽可能地远离,因此TWSVM的两个非平行超平面比SVM的一个超平面对样本不均衡问题的适应性更强。由于TWSVM训练速度较快,能较好求解异或问题以及分类性能优越等优势,它能够有效提高故障辨识精度[9]。本文将首先采用多种非线性特征对齿轮箱振动信号的非线性性进行测度,并采用Fisher准则[10]对非线性特征集进行评价,最后采用TWSVM方法对齿轮故障状态进行辨识。实验结果表明,非线性特征测度方法能够有效地提取齿轮箱振动信号状态特征,并且采用TWSVM分类模型其分类准确率要高于SVM和BP神经网络的分类准确率,因此可以看出TWSVM算法分类性能优势明显。
1 非线性特征的选取
基于非线性特征对于状态的敏感性和鲁棒性,本文选取分形维数和熵特征来提取齿轮箱振动信号的状态特征。对时间序列提取非线性特征一般采取相空间重构法,其原理是选择合适的延时时间τ和嵌入维数m对原始时间序列X={x1,x2,…,xN}进行相空间重构,如式(1),以还原混沌时间序列中蕴藏的非线性特征。
(1)

(2)
式中:H(u)为Heaviside函数
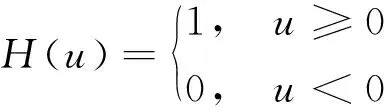
(3)
1.1 分形维数
分形维数是描述事物分形特性的一种有效方式,同时也是将事物分形特征进行量化的度量参数[11]。利用分形维数可以描述混沌时间序列吸引子的特征。分形维数的种类有很多,例如关联维数、盒维数和Lyapunov指数等,关联维数描述的是混沌时间序列具有某种确定的规律及程度,经相空间重构后的时间序列相互关联的点对个数越多,就表明系统运动的规律性就越强。
原始时间序列经相空间重构后,可得关联维数的表达式为
(4)
式中:C(r)为式(2)中的累计分布函数;r为阈值。Dc由lnr-lnC(r)坐标图中无标度区内的点用最小二乘拟合所返回的斜率值得到。
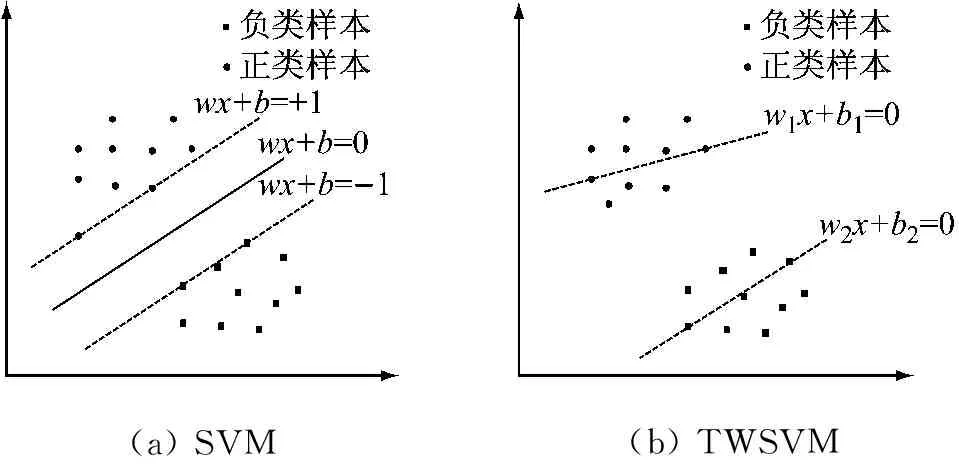
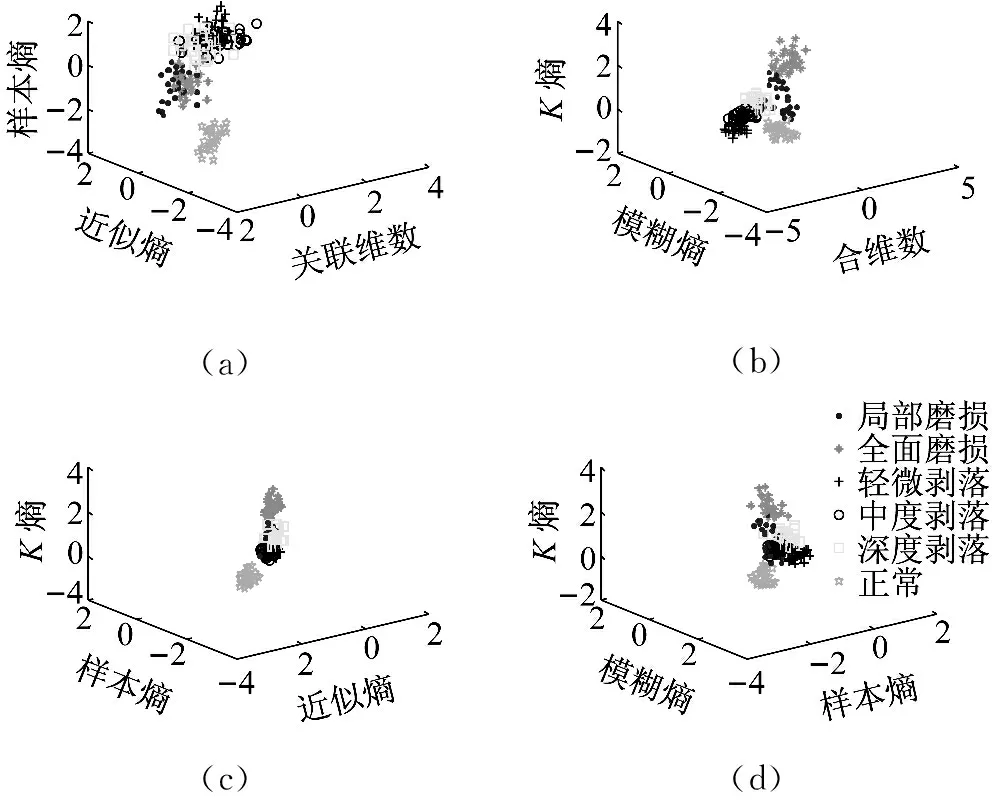
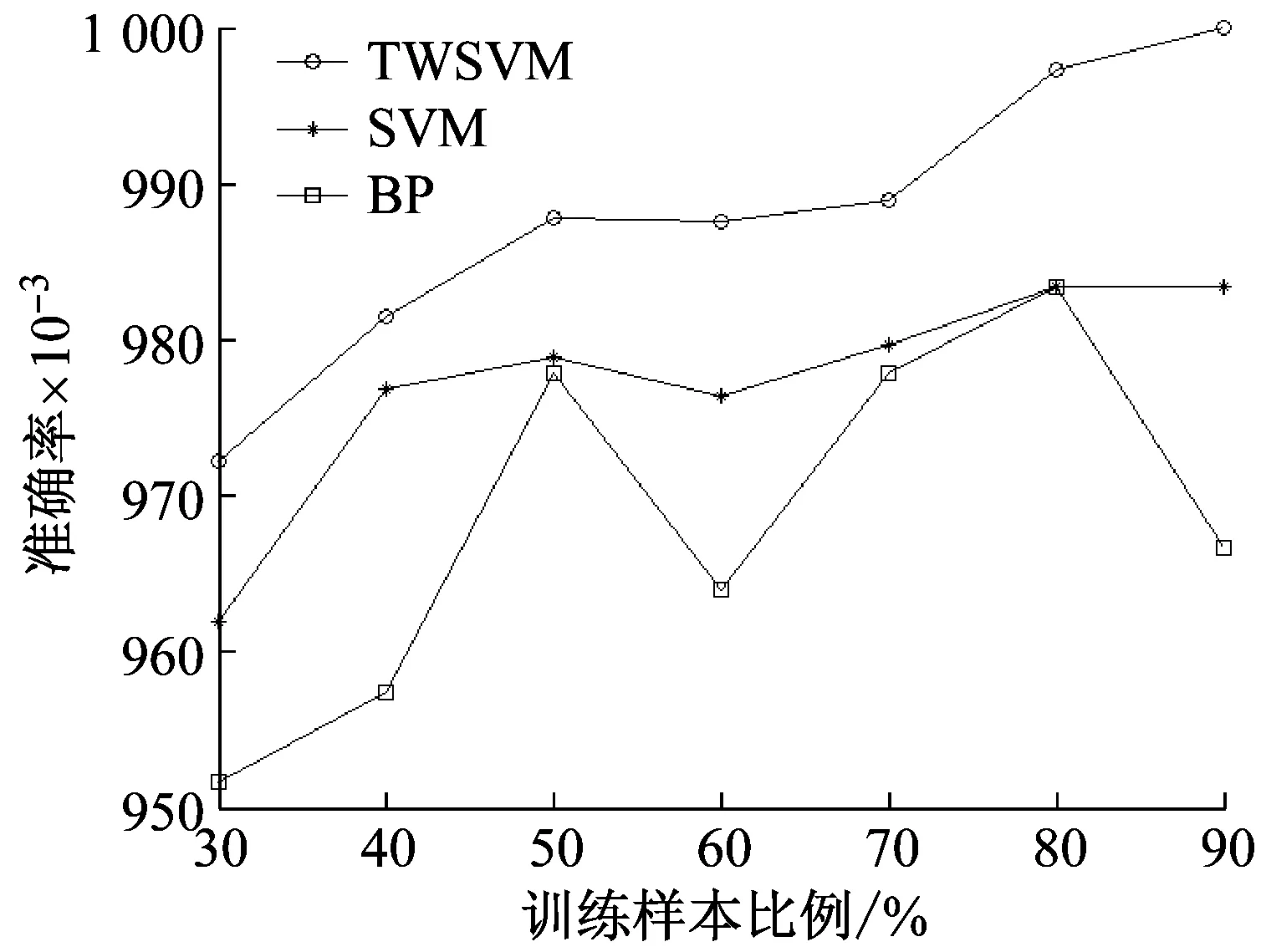
盒维数是将时间序列X划分为间隔尽可能小的网格,设Δ为基准网格然后以Δ为基准逐步扩大网格的宽度使其为kΔ,k=1,2,…,M,M DB= (5) 近似熵用来描述某时间序列的复杂性,越复杂的时间序列对应的近似熵值越大[12],其算法也是定义在相空间重构理论基础之上: (6) (7) 步骤4然后改变重构维数为m+1,重复上述过程可得φm+1(r),就可以得到近似熵 ApEn(m,r)=φm(r)-φm+1(r) (8) 由于重构维数m和阈值r的选取对于近似熵ApEn的计算值有较大影响,因此m和r的选取显得尤为重要,根据Pincus[13]在其论文中指出,当m=2,r=0.1-0.25SD(SD为时间序列标准差)时,近似熵值有较好的统计特性。 样本熵分析方法只需要较短数据就可得出稳健的估计值,是一种具有较好抗噪、抗干扰能力的非线性分析方法[14],其算法的步骤1和步骤2与近似熵算法的步骤1和步骤2,完全一样,在完成步骤1和步骤2后,样本熵计算步骤3如下 步骤3定义C(m)(r)为 (9) 步骤4增加维数到m+1,重复步骤2和步骤3可得 (10) (11) 步骤5定义样本熵为 (12) (13) 然后增加重构维数为m+1,重复上述计算过程,可得Φm+1(n,r),由此可得模糊熵FuzzyEn(m,n,r),即 lnφm+1(n,r)) (14) Kolmogorov熵值是非线性特性的度量量之一[16],是描述非线性系统产生信息量多少和快慢程度的物理量[17],其算法也是先对原始时间序列进行相空间重构得到累计分布函数Cm(r),无标度区内系统的Kolmogorov熵为 (15) 从定性的角度分析很难确定所提取特征样本的质量高低,为了能够定量地分析特征样本质量,这里采用Fisher准则方法对所提取的非线性特征进行评价。其中Fisher算法基本思路是针对整个样本集中第i个特征定义Fisher得分Fr为 (16) TWSVM比较于传统的SVM所建立的一个超平面,TWSVM构建了两个非平行的超平面,并使正类样本靠近正类超平面而负类样本尽可能地远离,使负类样本靠近负类超平面而正类样本尽可能远离,如图1所示。TWSVM将SVM的一个计算量大而复杂的二次规划问题转换为2个小规模的二次规划问题,减小了计算复杂性。由于使用非平行的分类超平面,TWSVM在解决两类样本成交叉分布的分类问题时,具有更强的泛化能力[18]。 (a) SVM(b) TWSVM 图1 SVM和TWSVM分类模型示意图 Fig.1 Classification model diagram of SVM and TWSVM 当样本是线性可分时,用线性的分类器就能够对预测样本进行分类,并能够保证其精度,并且计算量相对较小。当样本是线性不可分时,用线性的方法来训练分类器要么求不出解,要么得出的分类器测试精度很低。为解决线性不可分的问题,需要利用核函数将输入样本映射到高维特征空间,因为在高维特征空间中原来线性不可分的问题就变为线性可分。 非线性TWSVM的算法原理如下: 假设矩阵A代表第1类样本集,矩阵B代表第2类样本集,其中A∈Rm1×n,B∈Rm2×n。m1代表第1类样本数,m2代表第2类样本数,n代表特征向量维数。现在引入Mercer核函数,K(xi,xj)=φ(xi)Tφ(xi)。那么非线性的TWSVM的2个二次规划问题可以表示为TWSVM1和TWSVM2,即 TWSVM1 s.t. -(K(B,CT)u(1)+e2b(1))+ζ≥e2 ζ≥0 (17) TWSVM2 s.t. (K(A,CT)u(2)+e1b(2))+η≥e1 η≥0 (18) 针对TWSVM1和TWSVM2二次规划问题,采用拉格朗日法求解,可得TWSVM1和TWSVM2的对偶问题分别为式(19)和式(21),具体推导过程可参考。 TWSVM1 s.t. 0≤α≤c1 (19) 式中:向量α=(α1,α2,…,αm2)T,G=[K(B,CT)e2];H=[K(A,CT)e1],其余变量之前已定义。 从TWSVM1的对偶问题的推导中可以得出 (20) TWSVM2 s.t. 0≤γ≤c2 (21) 式中:γ=(γ1,γ2,…,γm1)T;P=[K(A,CT)e1];Q=[K(B,CT)e2]。 从TWSVM2的对偶问题的推导中可以得出 (22) 只要求得了u(1),u(2),b(1),b(2),那么就可以求出分类所需要的两个超平面 K(X,CT)u(1)+b(1)=0 K(X,CT)u(2)+b(2)=0 (23) 最终判别公式为 (24) 为了研究齿轮箱振动信号在非线性测度下的TWSVM辨识性能。本文选取由布鲁塞尔自由大学提供的不同状态类别的齿轮箱振动信号。其一共有5种故障类型和1种正常状态,共6种标签类型,分别为局部磨损,全面磨损,轻微剥落,中度剥落,深度剥落和正常。分别读取这6种标签下的振动信号,得到其时域波形,并对时域信号进行FFT变换得到其对应的频谱,如图2所示。 图2(a)中各小图分别对应标签为局部磨损,全面磨损,轻微剥落,中度剥落,深度剥落和正常的时域波形,图2(b)中各小图分别为局部磨损,全面磨损,轻微剥落,中度剥落,深度剥落和正常的幅值谱。时域波形仅从肉眼只能看出每种标签下的振动信号都是包含着噪声和调制的复杂信号,但是齿轮箱中的齿轮在实际运转过程中它会受到驱动力,弹性力和阻尼等因素的影响,另外齿轮啮合过程中摩擦力的变化、转速不稳定及其可能的突变性和轮齿的碰撞等会使得当齿轮出现故障时整个齿轮箱系统产生非线性振动,因此所测得的齿轮箱故障振动信号一般会表现出非线性和非平稳的特征。传统的时域和频域分析法很难从非线性振动信号中提取有效的状态特征,比如从图2中不能很明显地看到能够反映状态类别的特征信息。因此如果采用线性的方法来对信号提取特征,必然会丢失信号的非线性成分,那么采用非线性测度方法来对时域信号提取特征就显得尤为重要。 针对数据样本的6种标签,每类标签选取30个样本,每个样本截取1 024个点,一共构成180个数据样本,组成维数为1 024×180的数据样本矩阵。 分别对180个数据样本中的每个样本提取特征,每个样本共提取6个特征,要提取的特征分别为关联维数、盒维数、近似熵、模糊熵、样本熵和K熵。由此组成维数为6×180的特征矩阵并归一化处理,根据整体样本集中不同特征值随类别标签变化的统计规律及趋势选择了其中部分特征向量值得到如表1所示数据。从表1可以看出所选择的6个特征算法所得到特征值对故障类别较为敏感,并且随着故障程度的加深呈现出一致性的规律,如正常状态即无故障振动信号的特征值最小(即负得相对最多),在同种故障类型下,局部磨损和全面磨损相比,局部磨损的特征值要小于全面磨损;轻微剥落,中度剥落和深度剥落相比,轻微剥落的特征值要小于中度剥落的特征值,中度剥落的特征值要小于深度剥落的特征值。总结起来就是故障程度越小其振动信号的混沌特性越不明显因而特征值越小,而故障程度越大其振动信号的混沌特性也就越明显因而特征值相对较大。为了能够定量地对特征值进行评价,本文选用Fisher得分算法来对特征进行打分,对原特征矩阵进行归一化处理后,将特征矩阵输入到Fisher函数中,得到其结果如表2所示。 表1 部分特征向量参数 表2 Fisher算法打分结果 从表2中可以看出,K熵的得分最高,盒维数的得分相对较低,其他特征的得分处于这两者之间,为了更为直观地观察特征样本集在空间中的分布,将这6个特征中每3个特征一个组合,一共选取4个组合来分析特征的聚类程度,从图3中可以看出各种状态类别的特征值在空间中呈现出一定的聚集状态,呈块状或者云状分布。但是深入观察可以发现图3(a)~图3(d)中不同故障类别的特征值样本之间任有一些重叠,那是因为针对不同状态类别只选取了3个维度的特征值,在添加了剩余的特征维度之后,特征向量将被映射到更高维的空间中,其特聚类性将更加明显。综上所述,采用非线性特征方法能够有效提取齿轮箱状态特征。 (a)(b)(c)(d) 图3 3个特征值维度下的特征聚类分析 Fig.3 Clustering analysis of features based on three characteristic value 在每类标签30个样本中选定训练样本和测试样本的比例,为了比较不同训练样本的比例对TWSVM算法分类精度的影响,本文选择训练样本的比例分别为30~90%,剩下的作为测试样本集。 针对一共6类标签类型以及所确定的训练样本和测试样本的比例,随机抽取样本,以10折交叉检验的方法避免偶然性误差。表3给出了TWSVM在不同的训练和测试样本比例情况下的识别性能。 从表3可以看出TWSVM的训练准确率能够达到97.22%以上,并且随着训练样本比例的增加其准确率呈上升趋势,当训练样本比例为90%时,其准确率达到100%,这足以说明基于非线性特征测度的TWSVM有很高的分类准确率。 表3TWSVM在不同训练、测试样本数情况下识别性能 Tab.3RecognitionperformanceofTWSVMbasedondifferenttrainingandtestsamples 样本比例/%总训练样本数总测试样本数正确分类样本(10)次平均准确率/%3054126122597.224072108106098.1550909088998.78601087271198.75701265453498.89801443635999.729016218180100.00 为了体现TWSVM分类方法的优势,在同等条件下将TWSVM与SVM和BP神经网络进行对比,如图4所示。从图4中可以看出,TWSVM、SVM和BP神经网络3种算法的分类准确率都随着训练样本的增加而整体呈上升趋势,但是TWSVM算法随着训练样本比例的增加其准确率呈现较为均衡的上升趋势,而SVM和BP算法其准确率的波动性较大,特别是BP方法,当训练样本比例为60%和90%时其准确率有较大幅度的降低。 图4 TWSVM,SVM和BP分类准确率对比 特别地,当训练样本比例从30%一直上升到90%时,TWSVM算法的平均准确率整体上一直都高于SVM和BP算法,因此从整体上可以看出TWSVM算法要优于SVM和BP神经网络。另外值得注意的是本文不管是采用TWSVM还是SVM来分类,均采用的是偏二叉树方法来实现多分类目标,而偏二叉树方法必然会产生训练样本不均衡性问题,因此从试验结果可以看出TWSVM比SVM具有更高的样本不均衡适应性。 由于齿轮的振动一般是非线性的,因此对其振动信号提取特征需采用非线性特征测度的方法。本文选取了关联维数、盒维数、近似熵、模糊熵,样本熵和K熵,这6个非线性特征参数来对带有局部磨损、全面磨损、轻微剥落、中度剥落、深度剥落和正常这6状态类型的齿轮箱振动信号进行特征提取。并用Fisher得分算法对特征进行打分,另外用特征云图的方法对特征的聚类性进行直观地描述。另外为了体现出TWSVM算法的优越性,将其与BP神经网络和SVM算法的分类精度进行对比,可以得出如下结论: (1)采用非线性特征测度方法对齿轮箱振动信号进行状态类别分析,能够更加准确地辨识出齿轮箱工作状态,有助于后期构建准确的分类模型。 (2)采用TWSVM作为分类模型,以所提取的非线性特征集作为训练和测试样本集,得到在不同训练样本比例下的整体识别精度可以达到97.22%以上,训练样本比例越高准确率越高。在同等条件下TWSVM模型分类准确率整体上要高于BP神经网络和SVM,并且TWSVM具有更高的样本不均衡适应性。
1.2 近似熵、样本熵、模糊熵和K熵
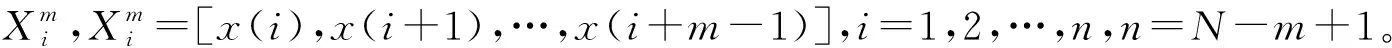



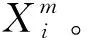
2 特征评价算法

3 非线性TWSVM原理




4 实验研究







5 结 论

