多维地震激励下结构碰撞振动台试验及碰撞影响参数研究
闫 磊, 李青宁, 岳克峰, 赵花静, 申纪伟, 王天利
(1.重庆三峡学院 土木工程学院,重庆 404100;2.西安建筑科技大学 土木工程学院,西安 710055)
历次破坏性巨大的地震中桥梁结构的震害表明,梁体与限位装置和邻梁之间的碰撞是导致桥梁结构局部损坏或落梁等震害发生的主要原因。一般情况下,桥梁结构某两联、两跨之间或者梁体与桥台之间的动力特性存在较大差别,相邻桥跨或者梁体与桥台在地震作用下会导致其上部结构的不同步振动,若伸缩缝处的预留距离小于相邻梁体间的相对位移时,相邻结构便会产生碰撞现象。桥梁结构之间一旦发生碰撞会使得梁体产生较大的冲击作用[1-2],以往的震害中因碰撞作用引起的伸缩缝破坏、主梁局部破坏、落梁、断墩、支座破损、桥台胸墙破损等震害屡见不鲜[3-4]。
已有研究表明,学者们对结构碰撞问题进行了较深入的理论研究[5-6]。目前,对于碰撞问题的研究方法主要有立体力法和接触单元法[7-9],立体力法是以经典力学理论为基础,结合动量和能量守恒定律进行分析,其优点在于概念明确、易于理解,但该方法有一定缺陷,其只适合于计算碰撞时间较短,碰撞自由度及接触位置较少的情况,且难以与商业有限元软件结合使用。接触单元法是在两个接触体之间设置接触单元,当两个结构发生碰撞时,接触单元被激活,接触单元参与计算,其具有计算精度较高且易于与有限元软件结合的优点。
在进行结构碰撞响应的理论与数值分析时,碰撞参数的选取具有一定的不确定性,不同的参数及计算方法会产生不同的计算结果[10-11],因此有必要进行地震作用下结构的碰撞试验,为碰撞理论的研究提供试验依据。目前,针对结构碰撞的试验研究还鲜有深入[12-13],对于结构在多维地震激励下的碰撞试验研究更是未见涉猎。
结构碰撞振动台试验能真实直观地反映结构间的碰撞现象,通过对试验现象的观察和数据分析,并结合相关理论,研究能够合理反应和模拟结构实际碰撞的分析方法,是目前碰撞问题的一个重要研究方向。基于此,本文设计并制作四组结构碰撞振动台试验,分析了振动台试验的结果,并在此基础上研究碰撞刚度、碰撞间隙、邻梁质量比、恢复系数等参数对结构碰撞响应的影响。
1 试验设计
1.1 模型设计
目前,常见桥梁结构如图1所示,在进行桥梁抗震设计时,常将伸缩缝两侧结构视为独立结构分别进行研究,对于梁体与桥台之间或梁体之间的伸缩缝简化成接触单元进行设计,图2为常用桥梁结构碰撞简化模型。
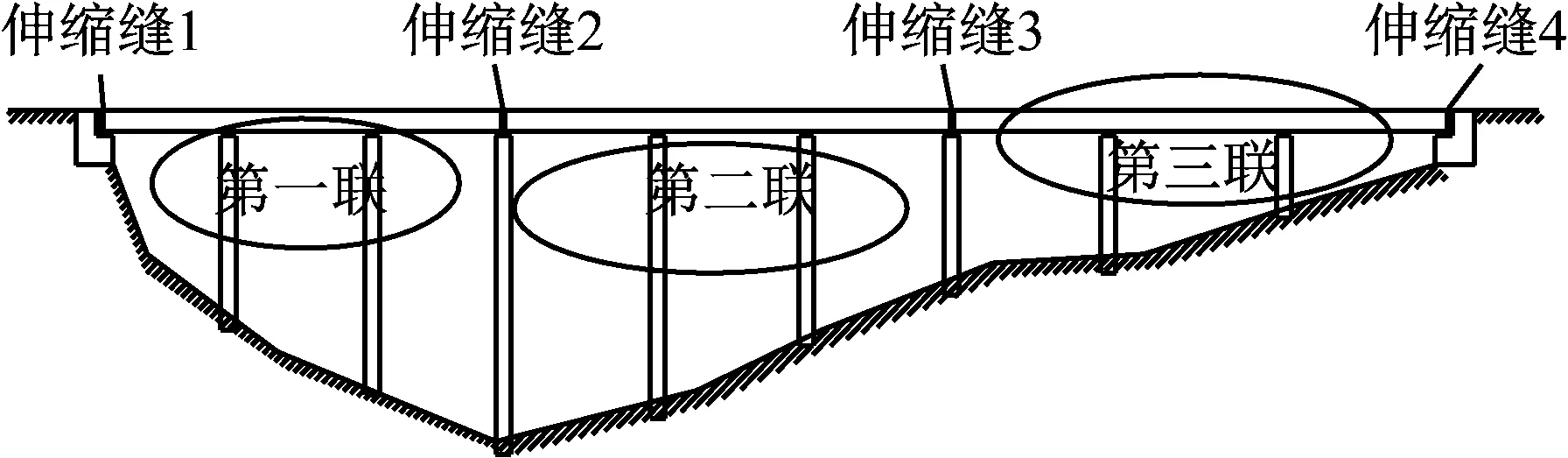
图1 桥梁结构
由于本试验旨在研究碰撞参数对桥梁结构碰撞响应的影响,故在模型试件的设计与制作过程中不考虑几何相似关系。碰撞装置制作材料采用钢材,共制作四组不同尺寸的碰撞构件,碰撞构件分别由碰撞铁块、螺纹钢、工字型钢组成。1#碰撞构件由5 cm×5 cm×15 cm铁块组成,2#碰撞构件由10 cm×10 cm×25 cm铁块组成,1#碰撞构件下侧焊接Ф22 mm螺纹钢筋,2#碰撞构件下侧焊接尺寸为100×68×4.5×7.6工字型钢,1#碰撞构件和2#碰撞构件间分别设置初始碰撞间隙gp。四组碰撞构件参数如表1所示。
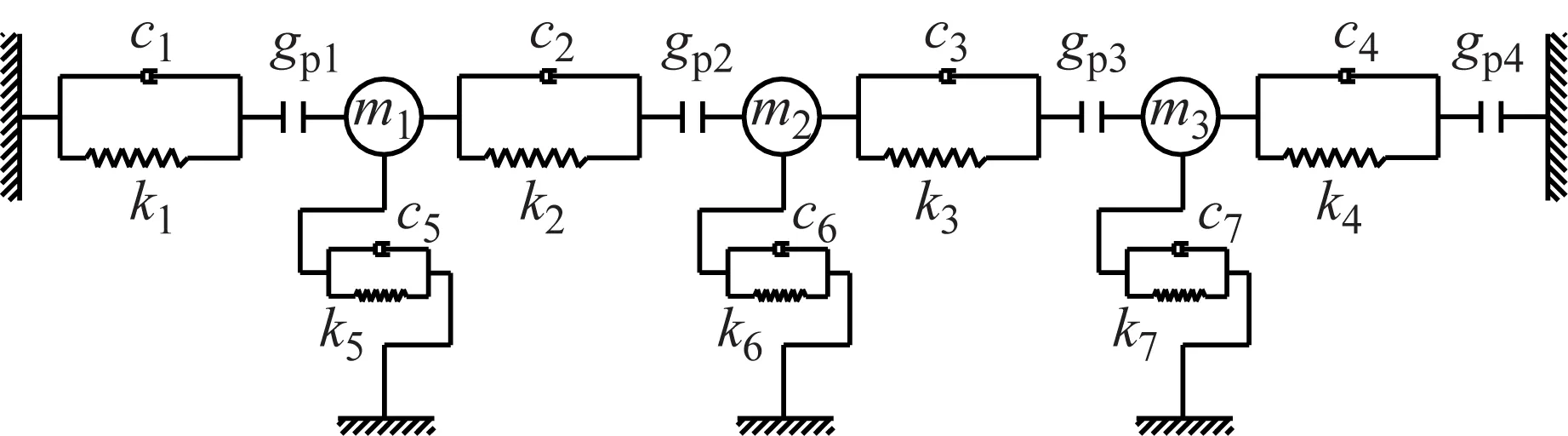
图2 碰撞简化模型
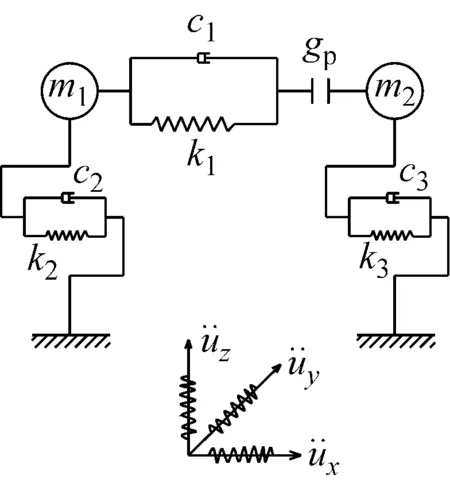
图3 理论碰撞模型
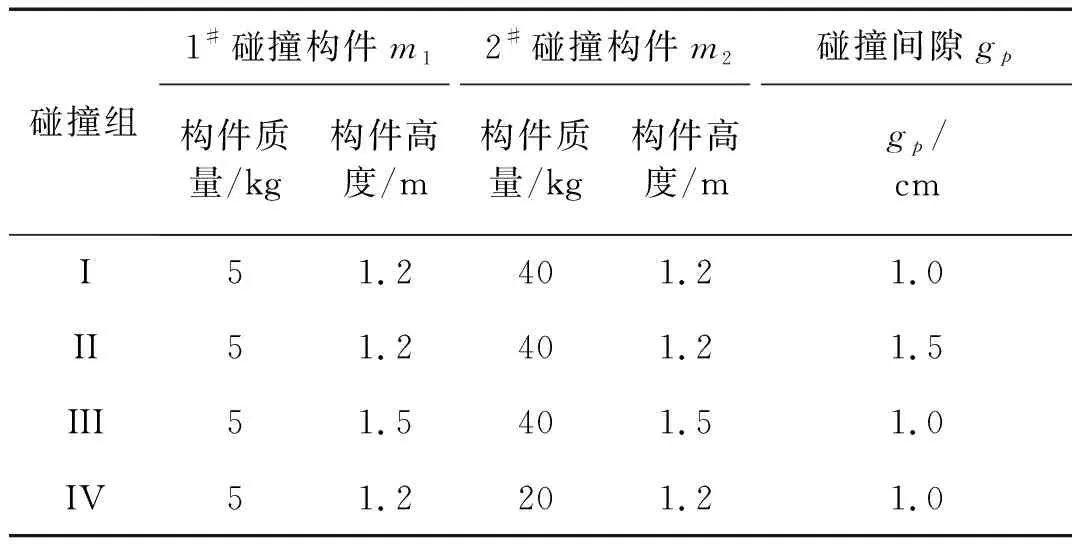
表1 碰撞构件参数表
根据以上预先设计的碰撞参数,设计出的碰撞模型如图4所示。
1.2 输入地震波及测点布置
为研究桥梁结构在多维激励下不同场地不同地震波强度对结构的碰撞响应影响,本试验在西安建筑科技大学三维六自由度振动台上进行。加载地震波选取El-Centro波、LZ波作为输入地震波,如图5所示。试验中将原地震波加速度峰值分别调整为0.50g,0.75g,1.00g,三向输入时地震波峰值按X∶Y∶Z=1.00∶0.85∶0.65进行调整。
本试验在碰撞构件上分别布置了加速度和应变传感器。其中加速度传感器共布置8个,分别布置在1#和2#构件的质量块上。应变传感器共布置8个,分别布置在碰撞钢柱和工字钢的底部。
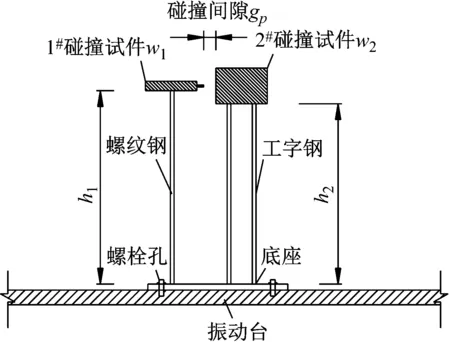
(a) 碰撞模型理论示意

(b) 碰撞模型振动台布置
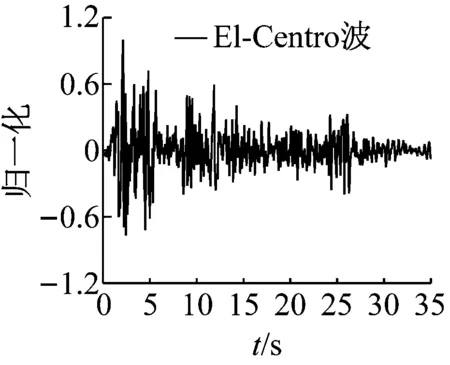
(a) El-Centro波
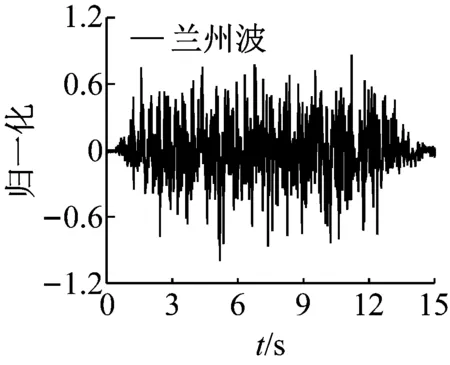
(b) 兰州波
2 试验结果分析
2.1 结构最大碰撞力值研究
强烈地震作用下,桥梁结构之间的相对位移超过其预设的初始间隙后会导致结构间产生碰撞现象。桥梁结构间剧烈的碰撞作用会引起构件的局部损环,甚至出现落梁等震害。桥梁结构碰撞是一种高度的非线性力学行为,其不仅会引起接触点的塑性变形、局部开裂等,也会引起相邻联、跨的桥墩底部弯矩及剪力需求的改变。在进行桥梁结构邻梁间、桥台与梁体间的防撞设计时最重要的就是要确定其最大碰撞力的大小。本试验忽略相似比设计,以四组碰撞构件为基础,研究了多维地震激励下碰撞对结构地震响应的影响。表2给出了多维地震激励下El-Centro波和兰州波引起的结构的最大碰撞力值,其中T1,T2分别代表1#,2#碰撞构件的自振周期。

表2 最大碰撞力
由表2分析可知:
(1)随着地震波输入加速度峰值的增加,相邻结构间的碰撞力逐渐增加。地震波的输入维度对结构碰撞响应有一定的影响,地震波的输入维度越多,相邻结构间的碰撞力越大。
(2)碰撞组II的最大碰撞力均大于碰撞组I,说明碰撞结构的高度对碰撞力有较大的影响。对于桥梁结构,相邻联或相邻跨的桥墩越矮,结构间的碰撞作用越小。
(3)两种地震波输入的结果都表明,碰撞组I的最大碰撞力与碰撞组III相比并无统一的规律,碰撞间隙的大小对结构最大碰撞力的影响并不是一个确定的量。因此在确定桥梁结构最优碰撞间隙时,要综合考虑结构类型、场地类别、接触刚度等因素。
(4)碰撞组IV的最大碰撞力均大于碰撞组I,分析原因是因为碰撞组IV的上部质量差异较小,导致两碰撞构件自振特性差异性较第I组大,因而其在地震作用下碰撞效应增强。故桥梁结构中相邻联或者相邻跨的自振周期差异性越大其碰撞响应越大。
2.2 数值分析与试验结果对比研究
目前,常用的四种接触碰撞模型分别为线弹性、Kelvin-Voigt、Hertz、Jan-Hertz-damp[14],四种碰撞模型由弹簧及阻尼组成,碰撞模型的力学计算方法如下。
(1) 线弹性模型
当相邻结构间相对位移超过初始间隙时,碰撞弹簧被激活,在碰撞过程中产生碰撞力。线弹性模型便于应用,但未考虑碰撞过程中的能量损失。碰撞力的计算公式为
(1)
式中:d为相邻结构初始间距;U2-U1为相邻结构间相对位移;kl为碰撞刚度;F为相邻结构间的碰撞力。
(2) Kelvin-Voigt 模型
Kelvin-Voigt模型由弹簧和阻尼单元并联而成,考虑碰撞过程中的能量损失,碰撞力的计算公式为
(2)
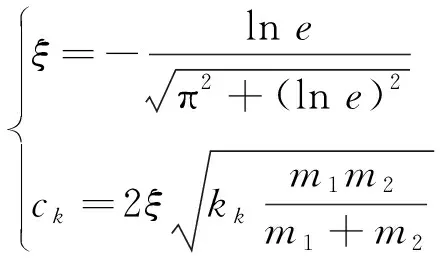
(3)
式中:kk为相邻结构的碰撞刚度;ck为黏滞阻尼系数;ξ为碰撞阻尼系数;e为碰撞恢复系数。
(3) Hertz模型
Hertz模型同样在计算过程中没有考虑碰撞过程中的能量损失,但碰撞弹簧是非线性的碰撞力计算公式为
(4)
式中:n为Hertz系数,一般取3/2;kk为相邻结构初始间距。
(4) Jan-Hertz-damp模型
Jan-Hertz-damp模型考虑接触体在碰撞过程中的能量损失。该模型假定结构在碰撞接触过程中可能发生塑性变形和局部损伤;在碰撞分离阶段,凝聚在相邻结构间的弹性应变能进行释放。接触过程中的碰撞力计算公式为
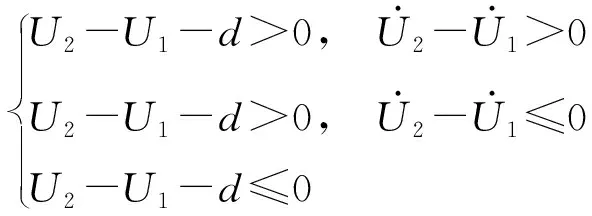
(5)
(6)
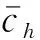
图6给出了El-Centro波激励下第IV组结构X单向试验时的碰撞力的时程曲线,根据结构最大碰撞力确定模型的碰撞恢复系数e为0.5。在此基础上,采用Matlab软件,嵌入四种碰撞单元,自编程序计算出四种碰撞单元的结构碰撞参数如表3所示。

表3 碰撞结构模型参数
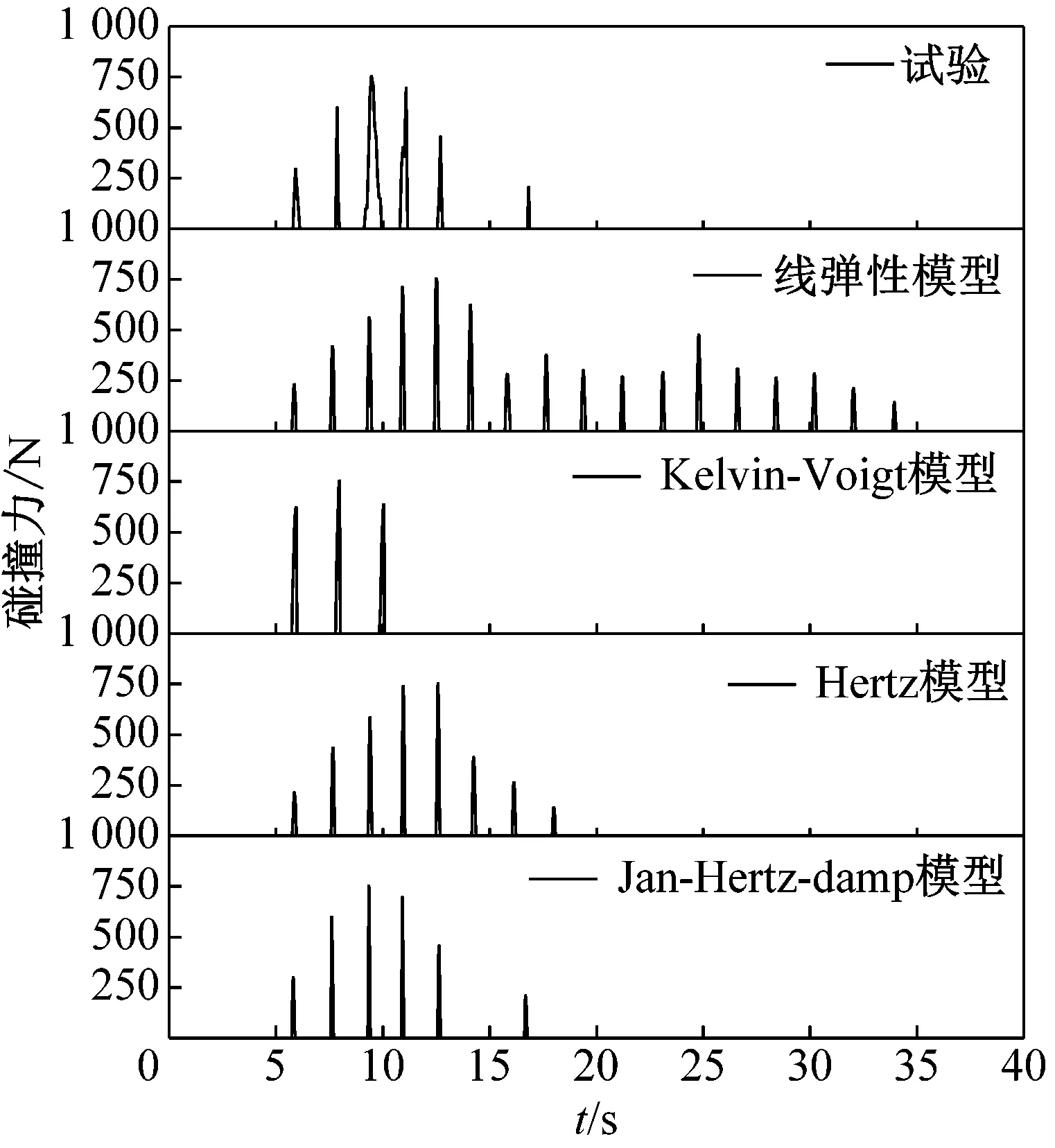
试验和数值计算所得到的0.75g和1g时El-Centro波X向激励后第IV组结构的碰撞力的时程曲线如图6所示。
从图6分析可知,针对不同碰撞单元,均可以选择合适的碰撞刚度模拟出与实际试验相同的最大碰撞力。由于线弹性和Hertz模型计算过程中不考虑结构在碰撞过程中的能量耗散,故其两种计算模型得到的碰撞次数较多,且碰撞时间间隔短,总体持续时间长。当碰撞单元采用Jan-Hertz-damp模型进行数值计算时,其结果与试验结果最为接近,说明结构在碰撞过程中属于弹塑性碰撞,碰撞恢复系数的选取也较为合理;同时,该模型在计算过程中由于判断语句及求解语句相比其他单元更趋复杂,因此计算耗时较多。
(a) 0.75g
3 结构碰撞影响参数分析
本节针对不同的结构碰撞参数,以试验结果为基础,选取常用的El-Centro波、兰州波、Taft波、Chi-Chi波、Hollisters波作为输入地震波。采用自编程分别计算地震作用下不同碰撞参数对结构碰撞响应的影响。
3.1 碰撞刚度取值对结构碰撞响应的影响
在实际桥梁结构中,相邻梁体之间的碰撞经常会引起梁体的脆性破坏或者落梁等震害,因此碰撞刚度的选取是否合适将直接影响着数值计算结果是否可以真实反映结构的真实碰撞力,本节研究碰撞刚度的取值对结构碰撞力的影响。
根据2.2节的研究结果,证明合理选取结构的碰撞刚度等参数,可以真实的反应结构的最大碰撞力,且针对弹塑性碰撞结构,合理的选取碰撞单元模型也是能否接近真实地反应结构碰撞响应时程曲线的重要影响因素。由表3分析可知,不同加速度峰值时结构的碰撞刚度取值不同,且无统一规律,但其基本上处于一个数量级上。
表4、表5为采用Jan-Hertz-damp模型,计算El-Centro波和兰州波在0.75g单向激励下不同碰撞刚度时的最大碰撞力计算结果。从表中数据可知,相同地震输入加速度峰值时,碰撞刚度对最大碰撞力的计算结果影响较大。总体上讲,当相邻结构的其它参数确定时,碰撞单元的碰撞刚度越大,相邻结构间的碰撞力越大。当碰撞刚度取值处于使结构产生的最大碰撞与实际结构比较接近的范围时,最大碰撞力的变化较小;当碰撞刚度与实际碰撞刚度相差较大时,计算出的碰撞力与实际试验结果相差较大。因此,对于碰撞结构,碰撞单元刚度的取值是否合适,直接影响着计算结果的准确与否。
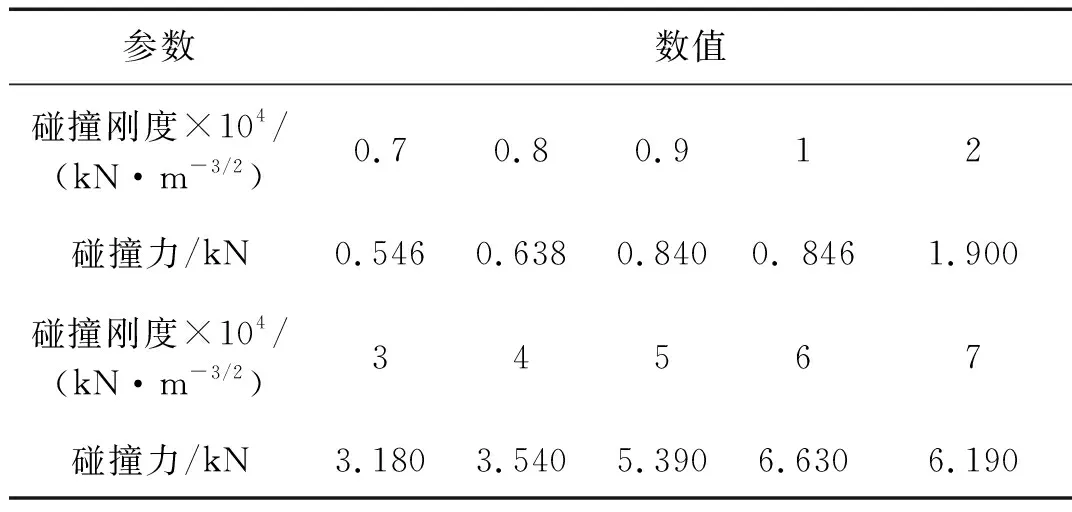
表4 EI-centro波激励下最大碰撞力
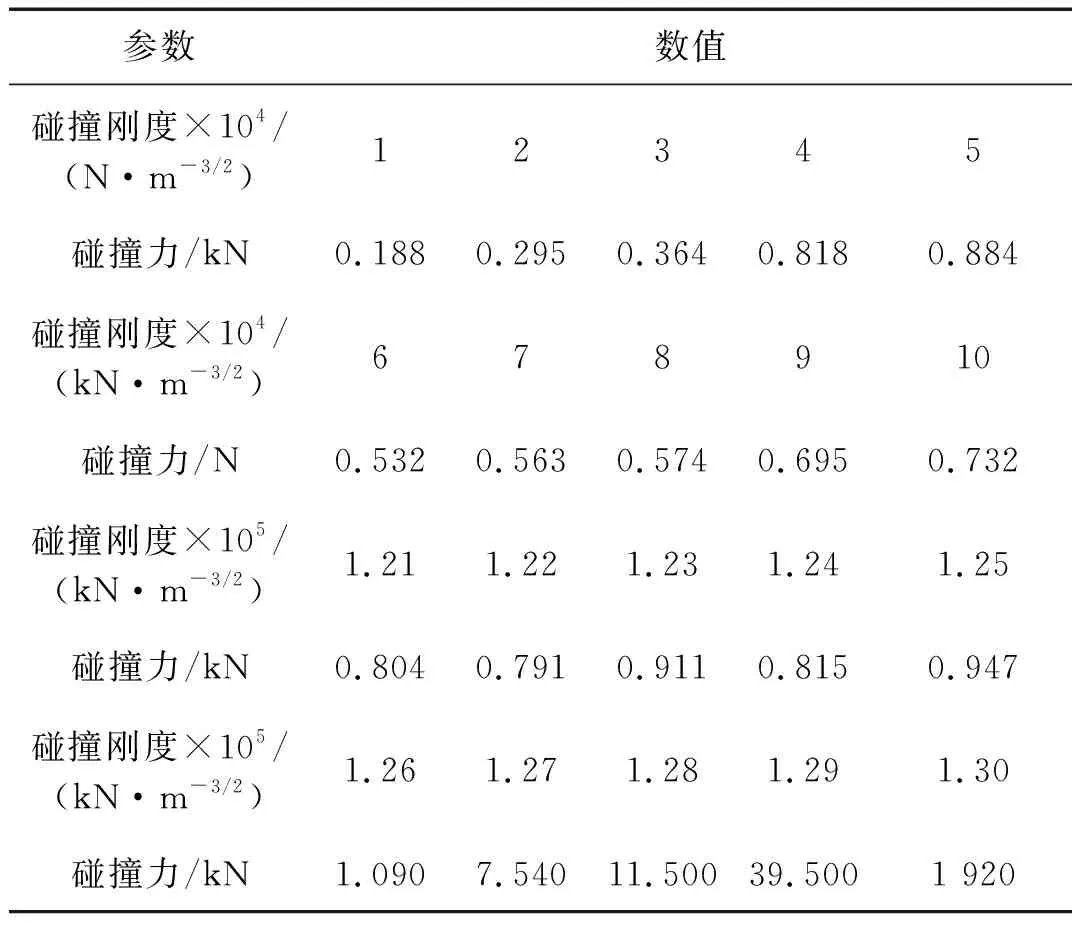
表5 兰州波激励下最大碰撞力
以往,学者们对于关于碰撞刚度的取值问题已进行了较深入的研究。Van Mier等[15]对Hertz刚度的取值问题进行了深入研究,结果表明Hertz刚度宜取1.2×106~2.6×106kN/m3/2。禚一等[16]运用接触刚度理论,建立了等效的Kelvin撞击模型碰撞刚度的确定方法,并给出适于城市梁桥地震碰撞反应分析的值取值范围为3×105~6×105kN/m。
以上试验均是基于混凝土结构和钢筋混凝土结构的碰撞研究,对于钢结构方面,Chau等[17]做了地震动激励下两钢塔碰撞的试验,并进行数值模拟,得出线弹性模型、Kelvin-Voigt模型、Hertz模型、Jan-Hertz-damp的刚度取值分别为1.40×106kN/m,1.40×106kN/m,2.36×107kN/m3/2,9.90×107kN/m3/2。Zhu等[18]经正弦波激励下的桥梁主梁与桥台碰撞试验和数值模拟,通过试验数据得出线弹性弹簧、Kelvin-Voigt模型、Hertz模型、Jan-Hertz-damp的刚度取值分别为1.547 4×102kN/m,1.547 4×102kN/m,4.15×103kN/m3/2,4.15×103kN/m3/2。
本文计算结果表明,当得到与计算结果相同的最大撞击力时,线弹性模型和Kelvin-Voigt模型的碰撞刚度取值明显不同,这与以往研究结论[19]关于其取相同刚度的结论不尽相同。在实际的碰撞结构模拟中,接触刚度的取值导致计算结果不一定能真实反映结构碰撞响应,且不同地震波输入时也有可能使得结构的计算碰撞刚度的取值得到改变。
3.2 初始间隙对结构碰撞响应的影响
初始间隙是结构间碰撞的一个重要影响因素,对于桥梁结构的碰撞问题,邻联或者相邻梁体的相对位移超过碰撞单元的初始间隙时,梁体之间发生碰撞。在复杂的碰撞过程中,结构的地震需求在不断改变。本节针对不同的初始间隙,选取El-Centro波、Taft波、Chi-Chi波、Hollisters波,并将四种地震波加速度峰值调整为1.00g。以结构组IV的相关计算参数为基础,建立结构碰撞模型,分别计算不同碰撞初始间隙与结构的最大碰撞力的关系。计算结果如图7所示。
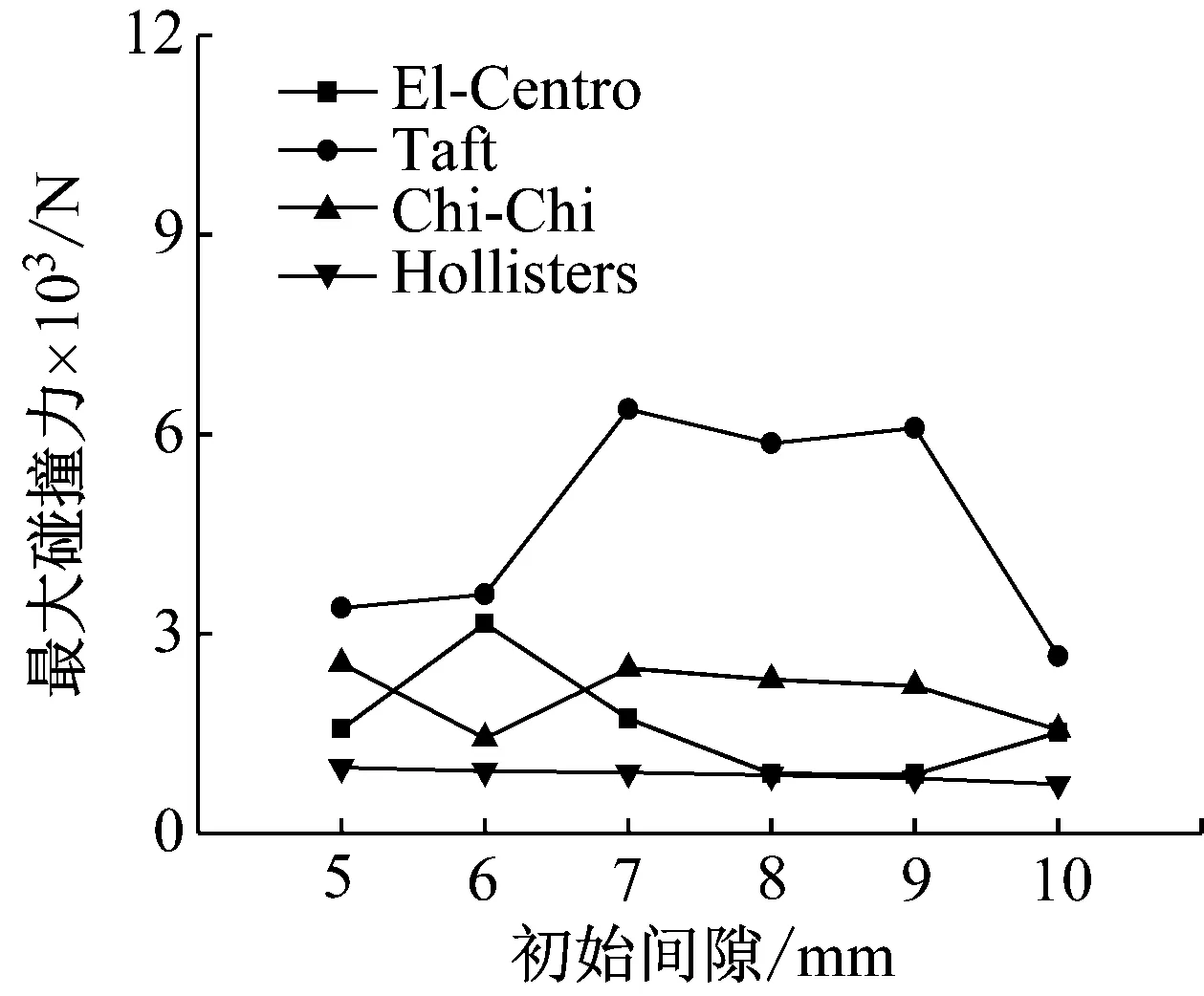
图7 初始间隙对纵向碰撞力的影响
从图7分析可知,不同地震波作用下,相邻结构的最大碰撞力受初始间隙的影响差异情况较大,不存在一个确定的初始间隙,能使得相邻结构产生最不利的碰撞力。因此,对于桥梁结构,伸缩缝的初始间隙是一个不确定因素,应针对不同结构的不同抗震需求进行设计。
3.3 结构高度对结构碰撞响应的影响
由于地形条件限制,一般山区桥梁或者城市高架桥梁桥墩高度变化较大,因此研究墩高变化对伸缩缝处碰撞力的影响显得尤为重要。本节以第IV组碰撞结构为基本模型,选取碰撞刚度k=8.8×106N/m3/2,初始间隙为10 mm,碰撞结构高度分别选取1 m,1.2 m,1.4 m,1.6 m,1.8 m,2.0 m,采用自编程序建立计算模型。分别选取El-centro波、Taft波、Chi-Chi波以及Hollisters波,将地震波峰值调整为1g,对模型进行地震激励,得到结构的最大碰撞力及1#碰撞构件底部的剪力如图8和图9所示。
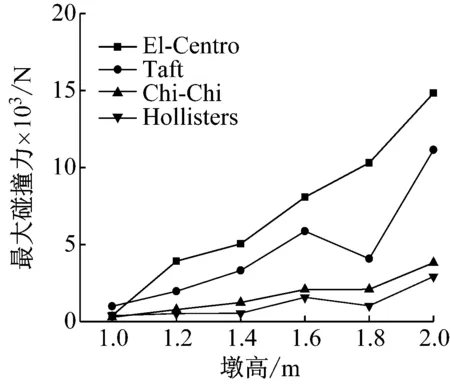
图8 不同结构高度最大碰撞力
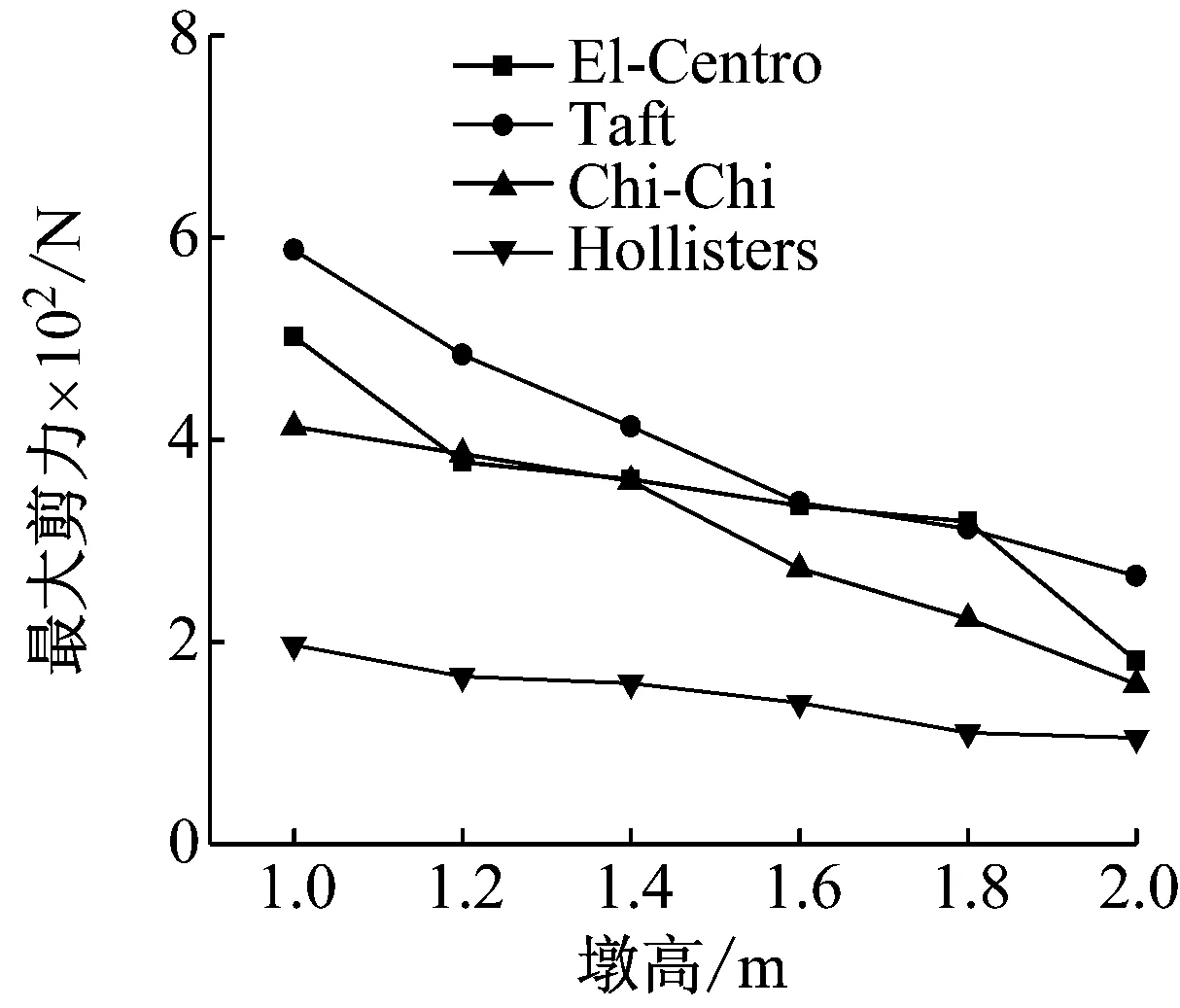
图9 不同结构高度最大剪力
图8可知,总体上讲,随着结构下部高度的增加,相邻梁体间的碰撞力增大。由此可见,桥墩高度对梁体纵向碰撞力的影响较大。图9可知:考虑碰撞效应时,结构底部剪力随着下部结构高度的增加而降低,说明对于桥梁结构,桥墩越矮,纵向碰撞引起的桥墩底部冲剪作用越明显。
3.4 碰撞结构质量比对结构碰撞响应的影响
桥梁结构在地震过程中,主梁由于其惯性力导致其在桥墩上方运动。然而惯性力的大小与其质量密切相关,因此有必要研究相邻结构质量对结构碰撞力的影响。为研究相邻结构质量对结构碰撞力的影响,本节选取相邻结构的质量比为1,2,3,4,5,6时相邻结构间的碰撞力大小变化情况。计算模型中碰撞刚度按照1.15×107N/m3/2,碰撞间隙按照10 mm设计,选取7.5.2节中的四种地震波,将地震波峰值调整为1g进行计算。图10和图11为不同邻梁质量比时结构的最大碰撞力。
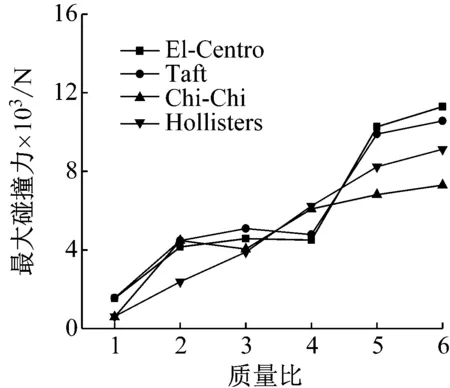
图10 质量比对最大碰撞力影响
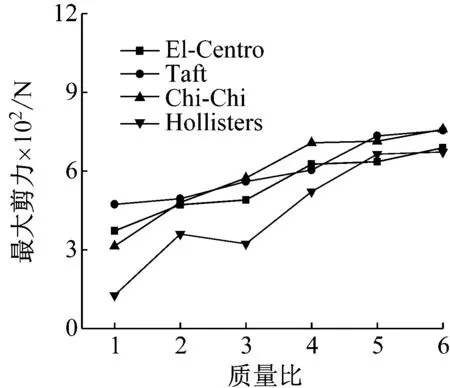
图11 质量比对最大剪力影响
从图10和图11分析可知,相邻结构之间的碰撞力随其质量比的增大而增大,结构底部剪力的大小亦随着相邻结构质量比的增大而增大。质量比最大的结构的最大碰撞力是质量比最小的最大碰撞力的14.79倍,质量比最大的结构的最大剪切力是质量比最小的结构的最大剪切力的5.3倍。说明相邻结构的质量比对结构的碰撞响应影响较大,实际桥梁结构设计中应尽量使相邻结构的质量比相差较小。
3.5 恢复系数对碰撞响应的影响
桥梁结构碰撞过程中常伴有能量的损失,能量损失情况常用阻尼c的大小表示。以往研究结果证明,阻尼的大小与结构碰撞的恢复系数e密切相关。为研究恢复系数对桥梁结构碰撞响应的影响情况,本节以碰撞结构IV为基础,建立碰撞模型,碰撞刚度取1.15×107N/m3/2,碰撞间隙按照10 mm,恢复系数分别取0.5~0.9。地震波仍然按照7.5.2节的四种地震波选取,峰值调整至1g。计算出的最大碰撞力随恢复系数的变化情况如图12和图13。
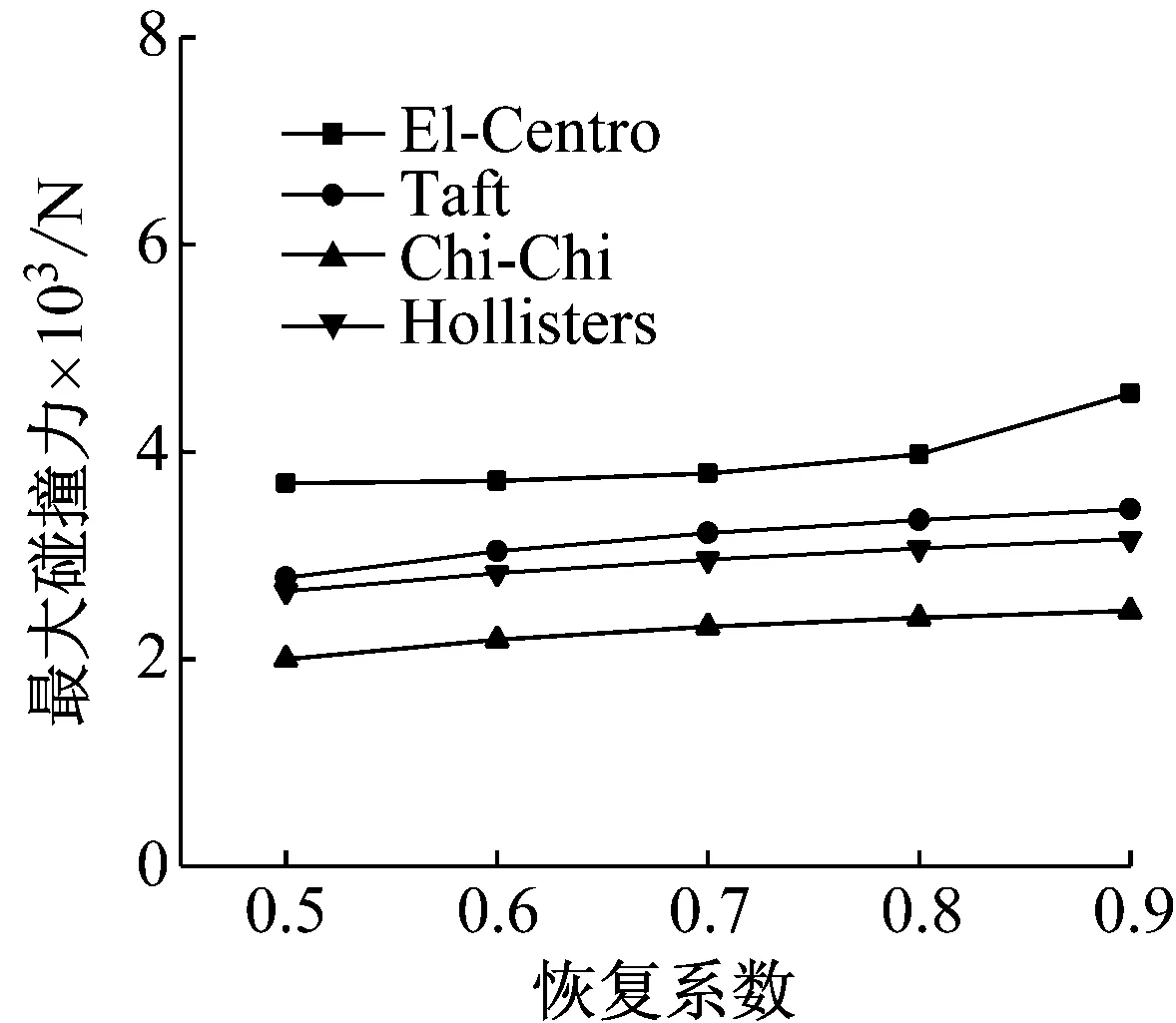
图12 不同恢复系数最大碰撞力
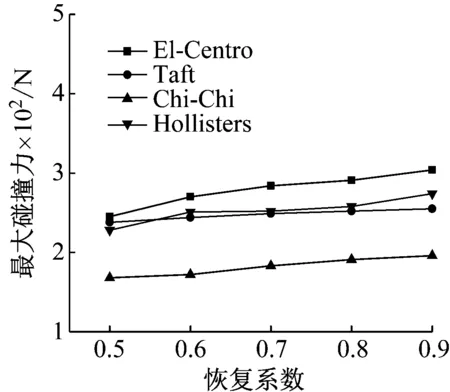
图13 不同恢复系数最大剪力
从图12和13分析可知,恢复系数对相邻结构间的最大碰撞力及结构底部的剪力均具有较大的影响。随着恢复系数的增大,结构间的最大碰撞力及结构底部剪力逐渐增大,对于不同地震波,其增大的幅度不尽相同。忽略结构碰撞过程中的能量损失,将不能真实反应结构间的最大碰撞力及结构底部剪力等效应,往往会过高估计相邻结构的最大碰撞力,引起材料的不必要浪费。因此,在进行桥梁结构的抗震设计时,应尽量在伸缩缝处设置高阻尼材料,达到增大结构阻尼,提高在邻梁碰撞过程中的能量损失。
4 结 论
本文进行了多维激励下相邻结构的碰撞振动台试验,对试验结果进行了详细研究,在此基础上分析了结构的碰撞参数对结构碰撞响应的影响。得到以下结论:
(1) 地震波的输入烈度以及输入维度对相邻结构间的碰撞力影响较大,烈度越大,维度越多,相邻结构的碰撞力越大。
(2) 四种碰撞单元均可以模拟出结构的碰撞效应,但Jan-Hertz-damp模型的计算精度最高,宜在碰撞计算中尽量选用。碰撞模型中接触刚度的取值导致计算结果不一定能真实反映结构碰撞响应,且不同地震波输入时也有可能使得结构的计算碰撞刚度的取值得到改变,因此在实际结构的碰撞模拟中,准确选择碰撞刚度尤为重要。
(3) 桥墩的高度对相邻梁体间碰撞力影响较大,桥墩越高,相邻梁体间的碰撞力越大,但是墩底剪力却与之相反。因此,实际设计过程中,必须选择一个最优桥墩高度,确保相邻结构碰撞力和墩底剪力相匹配,最大限度发挥结构中的材料性能。
(4) 碰撞间隙的大小对结构最大碰撞力的影响并不是一个确定的量,在确定桥梁结构最宜碰撞间隙时,要综合考虑结构类型、场地类别、接触单元刚度等因素。
(5) 相邻结构之间的碰撞力随其质量比的增大而增大,结构底部剪力的大小亦随着相邻结构质量比的增大而增大,实际桥梁结构设计中应尽量严格控制相邻跨或者相邻联的质量差异。
(6) 恢复系数的取值是否合适,将会影响到结构碰撞计算的准确性。随着恢复系数的增大,结构间的最大碰撞力及结构底部剪力逐渐增大,对于不同地震波,其增大的幅度不尽相同。因此,在进行桥梁结构的抗震设计时,应尽量在伸缩缝处设置高阻尼材料,增大结构阻尼,提高邻梁在碰撞过程中的能量损失。

