基于海量公交轨迹数据挖掘的地图匹配算法
陈 辉,蒋圭峰,姜桂圆,武继刚
(1.广东工业大学 计算机学院,广州 510006; 2.南洋理工大学 计算机科学与工程学院,新加坡 新加坡 639798)(*通信作者电子邮箱1164115502@qq.com)
0 引言
随着全球定位系统(Global Positioning System, GPS)技术的普及,基于车载GPS设备的轨迹数据挖掘已成为城市智能交通系统和定位服务研究的热点。尤其是海量的GPS轨迹数据为许多智能交通服务(如路径规划、实时导航和流行路线查询等应用)提供了数据支撑。然而实现上述各种服务的一个前提是能够将GPS轨迹数据准确地与数字地图上的道路相匹配(地图匹配),即使用车辆产生的GPS轨迹数据与底层道路拓扑网络相关联以获得车辆行驶的准确路线。
由于多种物理因素和现实原因,通过GPS获得的轨迹数据与实际道路之间存在偏差,造成了轨迹匹配的不确定性。导致这些不确定的因素有很多,如测量误差、采样误差、传感器故障或传输错误导致的数据丢失,因此正确识别行驶路段的地图匹配变得具有挑战性。Lu等[1]首先研究了基于轨迹匹配的不确定性,并提出了一种可视化方法来分析轨迹的不确定性。GPS设备精度导致的测量误差以及低采样率引起的采样误差使得地图匹配算法在处理低频轨迹数据方面面临困难。针对低频轨迹数据,目前主流算法大致可分为基于隐马尔可夫模型(Hidden Markov Model, HMM)[2]和考虑时空因素的基于时空匹配模型(Time and Space Matching Model, TSMM)[3]。Jan-Henrik等[4]在行人轨迹匹配场景中基于HMM提出了针对道路数据不完整情景的匹配方案,充分利用行人轨迹特点,应用HMM对转移概率和表现概率直接建模,简单有效,但匹配效果不甚理想且只针对特定应用场景,有一定的局限性。Liu等[5]提出一种全局时空地图匹配方法——时空条件随机场(Space-Time Conditional Random Field, STCRF),结合了时空信息,条件随机场模型解决了标注偏置问题,去除了HMM中两个不合理的假设,但模型变得复杂,效率也降低。Hu等[6]提出了一种使用多元复合信息(在经度、纬度、时间戳信息的基础上添加了速度、方向信息)描述移动物体的地图匹配模型,融合了多种相关信息,但需要更多更全面的轨迹数据;Yuan等[7]进一步研究了基于时空的匹配算法——基于交互式投票的地图匹配(Interactive Voting Map Matching, IVMM),它考虑了GPS轨迹的上下游位置信息的关系等其他因素。上述两文献在综合信息的前提上取得不错的匹配效果,但数据的信息维度过于全面和复杂,不适用于公交轨迹路线的匹配。
与上述研究相比,本文充分考虑了公交车线路与其他车辆的轨迹路线的不同之处:行车路线固定、多车同路线、运营时间规律、不间断、沿线路车站位置固定准确等特点,利用少量的数据信息维度(公交站点、轨迹点),通过一种基于海量轨迹数据挖掘的方法获得匹配轨迹序列,最后采用较为简单高效的HMM,取得良好效果。尤其需要指出的是,在处理低频轨迹数据的地图匹配时,现有方法试图构造最短连通道路以连接2个相距较远的轨迹节点,这种方法并不适用于公交轨迹数据,这是因为公交车线路并非刻意穿越最短旅行的路径,相反的,公交车线路为了方便更多的乘客会选择较长的路径。在公交轨迹数据挖掘中,融合多车同路线的不同时刻的轨迹数据面临诸多挑战:轨迹点的杂乱无序(不同时刻不同车辆采集得到)、数据存在测量误差、有较多异常数据等。为此,本文还将结合几何图形学、拓扑结构、模糊处理等理论方法。最后在实验部分,本文还提出了一种针对无标签数据验证的情况下,度量公交路线地图匹配结果精确度的可行方案。
1 相关工作
1.1 相关概念与定义
定义1 道路距离。道路两点之间沿地球表面的实际路面距离。
现实公交路线中路况比较复杂,根据路段的形状,大致可分为直线型、折线型、曲线型等,根据车道类别一般还可分为单向道、双向道,如图1所示。

图1 道路类型

(1)


图2 曲度计算


(2)
偏离度D表征了道路外的一点与该道路的靠近程度,该点越靠近道路偏离度越低;反之离道路越远偏离度越高。

图3 偏离度
1.2 HMM地图匹配算法
地图匹配算法以物体移动的位置序列为输入,得到物体移动过程所走过的连续道路序列。由于各种误差带来的噪声点,单纯地匹配每个点离它最近的道路将导致非常不合理,甚至出现循环行驶路径。HMM地图匹配算法以一定规则平滑地整合噪声数据,结合道路网络的连通性控制约束条件,计算多条可能路径的匹配概率,进而从中选择出一条最佳旅行路径。主要思想如下(如图4):对于t1时刻的待匹配点P,离它较近的有三条路段(实际候选路段),分别标记为R1、R2、R3(实心圆表示);t2时刻待匹配点P附近有两条可匹配路段R1、R2,t3时刻待匹配点P附近有一条可匹配路段R1。从t1到t3时刻车辆的真实行驶路段的可能情况就有6种:R1t1→R1t2→R1t3,R1t1→R2t2→R1t3,R2t1→R1t2→R1t3,R2t1→R2t2→R1t3,R3t1→R1t2→R1t3,R3t1→R2t2→R1t3。HMM地图匹配算法考虑所有路段Ri以及道路段之间的所有过渡情况,然后找到与实际行驶路径可能性最大的一条路径作为t1到t3时刻的最终行驶路径(具体算法细节请参阅文献[2])。
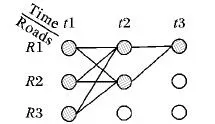
图4 路径搜索
2 公交路线地图匹配
2.1 公交路线地图匹配完整过程与思路
为更清晰地描述本文设计的基于海量公交历史轨迹数据挖掘的地图匹配算法,首先给出公交路线地图匹配过程的完整流程示意图,如图5所示。图5中,构建“高频、有序轨迹序列”是本文重点研究内容,即从海量低频、无序轨迹数据中构建出高质量的高频有序轨迹序列,其包含“模糊插值、精准剔除”两大处理过程。
由于公交站点序列具有有序且站点地理位置准确的特性,本文以有序公交站点作为公交路线轨迹序列的序列骨架,从大量无序的公交历史轨迹点中提取出数量足够、分布均匀且有序的公交轨迹点填充于序列骨架之中,形成用于公交路线地图匹配的完整有序轨迹序列。为方便描述,令BSL=〈S1,S2,…,Si,…,Sn〉表示稀疏而有序的公交站点序列——“序列骨架”,PL={G1,G2,…,Gj,…,Gm}表示公交车历史轨迹点的集合。据前所述:序列骨架BSL有序且稀疏,具有有序、低频的特性;PL是轨迹点集合,具有海量、无序的属性。精准的地图匹配需要高质量的高频、有序的轨迹序列点。本文从海量、无序的历史轨迹点集合PL中选取适量的、高质量轨迹点,将其正确地插入到序列骨架BSL中,得到有序的轨迹序列RPL:
RPL=〈S1,Gp,S2,…,Gq,…,Si,…,Gr,…,Sn〉;
Gp,Gq,Gr,…∈PL
在构建RPL的过程中,需要解决的挑战性问题包括:1)如何从海量无序的公交历史轨迹点集合中筛选、提取出适量且高质量的轨迹点;2)如何将选取到的轨迹点插入到序列骨架BSL的正确位置上,使之成为高频、有序的轨迹序列。本文将针对问题1)、2)所采取的处理过程称为“道路插值”,示意图如图6。
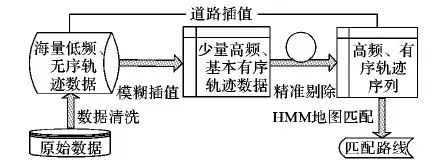
图5 地图匹配过程

图6 道路插值
2.2 道路插值之模糊插值
对2.1节提出的挑战性问题,首先利用数据分析与处理技术,将海量原始数据经过提取、转换、去重、重组等手段为每一路公交路线生成数量足够的历史轨迹点数据。将公交路线以站点作为切分点,将公交路线切分为若干路段,站与站之间的路段作为独立考察的“路段”。根据1.1节定义2中曲度(C)概念,设置系数δ∈[1,+∞),将路段统一聚类划分为“近直线型”路段和“曲线型”路段。根据曲度值的大小动态设置各个路段上插入点的数量,曲度越大的路段需要更多的插入点,以保证寻得完整的轨迹路线。
“模糊插值”理论分析如下(具体算法如算法1)。


条件1 ‖AB‖=max{‖AB‖,‖OA‖,‖OB‖};

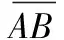

条件1 ‖AB‖=max{‖AB‖,‖OA‖,‖OB‖};
条件2 点O到直线|AB|的距离范围为0≤h(O⊥|AB| )<α,α∈(0,‖AB‖/2)。
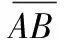

图7 候选轨迹点

算法1 道路插值之模糊插值算法。
Input:RS表示以公交站点为节点划分的路段集合,包含路段宽度、道路距离等信息;PS为各路段海量轨迹点集合。
Output:CRPL表示高频、基本有序轨迹序列。
CRPL←RS;
//初始化路线轨迹序列
setδ← [1,+∞);ξ← (0,λ/d);α← (0,d/2);
//参数设置,λ为路段宽度,d为路段的道路距离
forriinRS所有路段do;
ifC<δdo;
//ri为直线型路段,C为路段ri曲度值
forpijinPSido;
//PSi为路段ri上的轨迹点集合
if ‖AB‖=max{‖AB‖,‖pijA‖,‖pijB‖} and 0≤D(pij,ri)<ξdo;
//A、B为路段ri的两端点,
//D为点pij的偏离度
CRPL+=pij;
//将点pij插入路段轨迹序列中
end if
end for
end if
else do;
//ri为曲线型路段
forpijinPSido;
if ‖AB‖=max{‖AB‖,‖pijA‖,‖pijB‖} and 0≤h(pij⊥ri)<αdo;
//h(pij⊥ri)为点pij到路段ri的垂直距离
CRPL+=pij;
end if
end for
end else
returnCRPL;
2.3 道路插值之精准剔除
2.2节“模糊插值”过程中,“曲线型”路段上被选中的部分不属于该路段的轨迹插入点会造成该路段轨迹序列错序,且由于现实原因,搜集到的轨迹点中必定存在异常值。这会导致仅经过一次“模糊插值”过程无法得到完全正确有序的轨迹序列。为此,在“模糊插值”之后,还需要“精准剔除”处理,理论分析如下(具体算法如算法2)。


‖didk‖=max{‖didj‖,‖djdk‖,‖didk‖}
(3)
成立。依据式(3),便可剔除由“模糊插值”过程产生的路段轨迹序列中不符合条件的异常点和错序点。根据曲度值的大小设置路段轨迹插入点的数量,删除距离非常近的轨迹点以减小地图匹配时的计算代价,使基本正确、有序的轨迹序列最终成为高频、有序轨迹序列。
算法2 道路插值之精准剔除算法。
Input:CRPL表示高频、基本有序轨迹序列;
//算法1的输出
Output:RPL表示高频、有序轨迹序列。
setd← [1,10];t← [1,5];
//设置参数
whilet>0 do;
forGiinCRPL所有轨迹点do;
if ‖GiGi+2‖≠max{‖GiGj‖,‖GjGk‖,‖GiGk‖} do;
ifGi+1,Gi+2not stopid do;
//非公交站点
delGi+1,Gi+2;
//删除错序点
updateCRPL;
end if
end if
if ‖GiGi+2‖ ifGi+2not stopid do; delGi+2; //删除过于密集的点 updateCRPL; end if end if end for t--; RPL=CRPL; returnRPL; “模糊插值”实现了将相距一定距离的轨迹点插入到对应的路段之间,保证路段之间的插入点基本有序。“精准剔除”将路段之间错序的轨迹点和异常点剔除,重复该过程直至路段的轨迹序列保持有序。经过上述两个过程之后,得到高质量的高频有序轨迹序列,将其作为输入数据应用于1.2节说明的基于隐马尔可夫模型(HMM)地图匹配算法,得到最终的地图匹配路线,具体算法如算法3。 算法3 基于HMM地图匹配算法。 Input:RPL表示高频、有序轨迹序列; //算法2的输出 Output:MapRoute为地图匹配路线。 MapRoute← ∅; forpiinRPLdo; map_point=Alg_HMM(pi,parameters); MapRoute+=map_point; //加入匹配后的点 end for returnMapRoute; 本文批量处理的有效城市公交数量多达400多条,数据来源于新加坡陆路交通管理局提供的数据接口。包含两大数据集(以下简称“数据集A”“数据集B”)。数据集A是每间隔2 min对所有运行公交收集一次的相关信息,数据集A包含了海量的公交车轨迹数据,具有很大潜在的价值;然而其所包含的位置信息具有一定的测量误差、冗余数据和异常值,并且是无序的。数据集B是包含所有公交路线的站点有序序列信息,以及该公交车站距离始发站的实际路面距离(Distance/km)。数据集B的优点是有序且位置准确,缺点是过于稀疏。 本文所拥有的实际数据中,由于公交路线数量过多且没有用于直接计算的路线标签数据。为此,本文提出如下方法进行验证算法的效果与性能。 假设某一公交路线有n个车站,路线的道路总长度为L,地图匹配后得到的有序轨迹序列为: RPL=〈S1,G1,G2,…,Gp,S2,Gp+1,Gp+2,…,Gq, …,Si,…,Gr,…,Sn〉 其中:Gp,Gq,Gr,…为路段上的点,Si(i∈[1,n])为公交车站。 其中li,i+1,…,i+j-1表示连续路段i,i+1,…,i+j-1的距离之和,当j取不同值时,表示每j个路段作为一个距离计算单位。如图8所示,展示了随机选择的4条不同公交路线随着路段数j的增加而变化的MARE值,右上角图例中的数字代表公交路线编号。 图8 不同j值对指标值的影响 为此,选择j=2、3、4作为路线匹配精确度的度量指标,如图9所示,展示了随机选择的20条公交路线匹配后的指标值(为方便观察,对j=2时的MARE值作了排序),从中可以看出,当选择j=2、3、4时,指标具有一致的趋势,随着j值的增加指标值会稍有降低,j=2时指标值最差,但它的度量能力最强,更能反映地图匹配的精确度与细节匹配的吻合度。统计所有公交路线的匹配结果得出如下结论:当j=2时,接近50%的公交路线匹配结果的精确度达到90%+,80%的公交路线匹配结果的精确度达到80%+。 图9 j=2、3、4时部分公交路线匹配结果的指标值 以某度地图显示的路线结果为参考标准,从精确度达90%+的公交路线中随机抽取几条路线匹配结果与某度地图显示的路线图相比较,路线匹配结果几乎一致,如图10~11所示,这表明,上述提出的度量指标在无路线标签数据条件下,对匹配结果的度量与验证表现出很强的合理性。 图10 3路公交路线匹配结果 本文完整模型算法的实现包含三大子算法(算法1、2、3):数据挖掘算法(算法1、2)是在Ubuntu系统下使用Python平台实现;地图匹配算法(算法3)的实现使用了barefoot开源库(https://github.com/bmwcarit/barefoot)以及Open Street Map开源地图服务平台。海量公交历史轨迹数据经过数据挖掘算法处理之后,得到少量高质量、高频轨迹数据,大幅度减小了匹配算法在地图匹配时的数据规模及匹配时间(如表1)。如表2所示,随机选择了5条公交路线的匹配结果作展示,以3.2节提出的地图匹配精确度指标作为衡量标准,将挖掘算法得到的高频轨迹数据作为地图匹配算法的输入,与未经过挖掘算法处理的单车辆低频轨迹数据的匹配结果相比,公交路线地图匹配的精确度均有显著提高。 图11 36路公交路线匹配结果 Tab. 1 Comparison of various indexes before and after trajectory data mining 表2j=2时地图匹配算法精确度对比% Tab. 2 Precision comparison of map matching algorithms whenj=2 % 公交路线编号MARE经挖掘处理未经挖掘处理34A_13.849.45201_15.0213.65172_112.7015.8266_215.2919.10170X_219.6325.57 针对现有地图匹配算法对于低频轨迹数据匹配效果不理想的难题,本文提出的基于海量数据驱动的高频轨迹数据挖掘方法,为实现准确地图匹配提供可行、有效的数据输入,取得了比传统基于HMM地图匹配算法更好的匹配效果,为在缺少标签验证数据情况下的地图匹配结果提供了一种较合理的度量指标与验证方案。在得到准确公交路线的地图匹配结果后,将进一步研究车辆速度的估算以及车辆到站的时间预估等应用。2.4 基于HMM的地图匹配
3 实验结果及分析
3.1 数据说明与分析
3.2 地图匹配精确度的度量方法

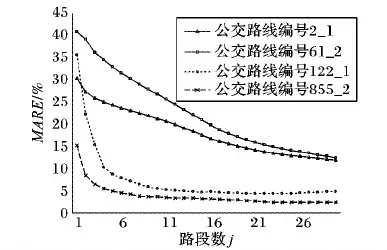


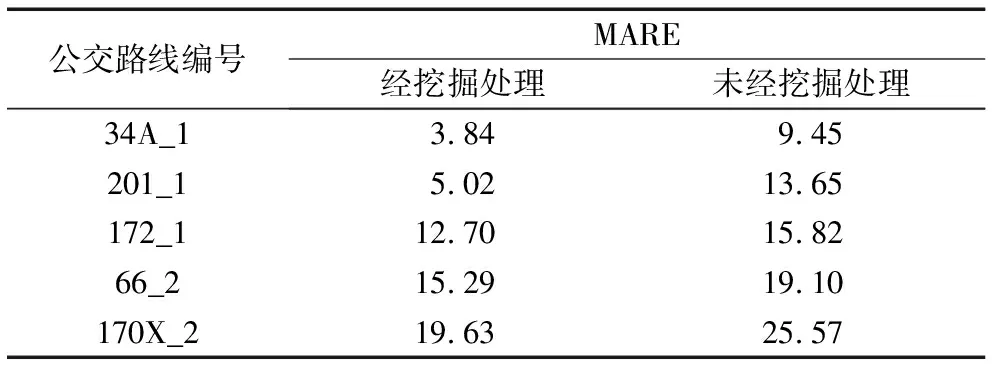
3.3 算法性能与效率分析


4 结语

