基于空-谱融合网络的高光谱图像分类方法
欧阳宁,朱 婷,林乐平
(1.认知无线电与信息处理省部共建教育部重点实验室(桂林电子科技大学),广西 桂林 541004;2.桂林电子科技大学 信息与通信学院,广西 桂林 541004)(*通信作者电子邮箱lin_leping@163.com)
0 引言
高光谱图像(HyperSpectral Image, HSI)具有光谱分辨率高、图谱合一的独特优点[1],已被广泛应用于目标追踪、环境保护、农业监测及气象预报等领域[2-4]。对高光谱图像中每个像元进行分类是高光谱遥感应用的基石,具有极大的研究意义。
传统的高光谱图像分类方法往往仅利用光谱信息在低维空间上提取特征,典型的方法主要包括:K-均值聚类(K-means)方法[5]、流形学习(Manifold Learning)[6]、支持向量机(Support Vector Machine, SVM)[7]等。然而,这些分类方法依赖于浅层光谱特征,忽略了对高光谱空间信息的使用,同时所提取高光谱图像特征的不变性及判别性较差。为了改善高光谱图像的分类性能,联合利用高光谱图像的光谱和空间信息设计分类器已成为一个主要的研究方向。近年来,深度学习以其在视觉感知任务中的优秀表现获得了广大高光谱分类研究者的热切关注[8-12]。Liu等[13]将高光谱图像的光谱带看作一个图像序列,使用长短期记忆网络学习光谱信息的依赖关系,同时结合卷积神经网络来提取高光谱图像的空间特征,提出了双向卷积长短期记忆网络(Bidirectional Convolutional Long Short Term Memory, Bi-CLSTM)空-谱提取模型;另一方面,Yang等[14]构建双通道卷积神经网络(Two-channel Convolutional Neural Network, Two-CNN)分别对光谱信息和空间信息进行提取,继而使用级联(concatenate)的方式对空-谱特征进行连接,但这种简单的特征连接方式并不能捕捉空-谱特征之间的复杂关系;Zhang等[15]在此基础上对光谱通道和空间通道不同层的特征进行级联,实现空-谱分级特征融合的效果。该工作在高光谱图像分类中,为从双通道特征提取角度进行空-谱特征结合提供了新思路,但该方法在特征结合方式上使用的仍是简单的点积方式。
目前,为了联合空-谱特征进行高光谱图像分类,大部分方法都采用级联或者点积的方式获得空-谱联合特征向量[14-15];但这些方法仅仅是对特征进行简单的连接,产生的空-谱联合特征向量并不能完全捕捉高光谱两个模态之间的复杂联系。在特征结合方式中,不同于级联或点积,双线性池化计算两个向量的外积,即能够捕捉两个向量中所有元素之间的乘法交互关系,其已经展示出在细粒度视觉分类中的有效性[16]。然而,双线性池化由于采用外积计算策略,也带来了维数急剧增加、计算复杂的问题。为了解决这一难题,Gao等[17]在单一模态下对双线性池化维数压缩方法进行了研究。本文受此启发,将压缩双线性池化推广到多模态条件下,从光谱和空间特征向量中每个元素相互关系的角度入手,探究高光谱图像中光谱和空间信息之间的联合特征表示。
根据高光谱图像的数据特点,针对高光谱数据维数高,简单的点积或级联方式所获得的空-谱联合特征表达能力弱的问题,搭建双通道网络模型,利用1-D和2-D卷积核分别提取高光谱图像的光谱和空间信息,并从空-谱特征融合的角度,采用多模态压缩双线性池化(Multimodal Compact Bilinear pooling, MCB)来获得空-谱联合特征,提出一种基于空-谱融合网络(Spatial-Spectral Fusion Network, SSF-Net)的高光谱图像分类方法。多模态压缩双线性池化先将双通道所提取的光谱和空间特征向量的外积随机地投射到更低的维数空间,继而在快速傅里叶变换(Fast Fourier Transform, FFT)空间中将时域中向量的外积运算转换为频域中使用点乘对两个特征向量进行卷积。最终,将产生的空-谱联合特征输入最后的线性分类器,用以对高光谱图像每个像元分类。多模态压缩双线性池化既可以在像素级别充分融合双通道所提取的空-谱特征,同时也避免了单特征直接外积计算所带来的维数增加、计算困难的问题。实验结果表明本文提出的算法可以获得更高的像元分类精度。
1 基于空-谱融合网络的高光谱图像分类框架
为了充分利用高光谱图像的空-谱联合特征进行像元分类,本文设计了双通道(光谱通道和空间通道)卷积神经网络结构分别学习光谱域和空间域的特征;同时,使用多模态压缩双线性池化方法对所提取的多模态特征进行融合,以此来探索空-谱特征的相关性,改善高光谱图像的分类性能。本文所提出的高光谱图像分类网络框架如图1所示,其展示了网络的两个特征提取通道及多模态特征融合层的具体结构。
光谱通道 选取原高光谱图像第n个像素的光谱带sn∈RM×1(其中M为光谱带长度)作为光谱通道的输入,此后使用1-D核对光谱输入进行卷积和最大池化操作,在光谱通道的全连接层获得光谱通道的输出特征f1(sn)∈RK×1(其中K为全连接层的神经元个数)。
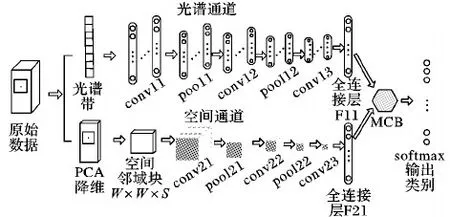
图1 空-谱融合网络整体框图
空间通道 首先,对原高光谱图像在光谱维度上进行主成分分析(Principal Component Analysis, PCA)降维处理,压缩后的光谱维数为S(S≪M)。这一步会丢掉一部分光谱信息,但图像的空间信息不会受到影响;其次,在降维后的高光谱图像中,选取与光谱通道输入相对应的第n个像素邻域块Pn∈RW×W×S(其中W为空间邻域块的长宽尺寸)作为空间通道的输入,其后利用2-D核对空间输入进行卷积和最大池化操作,在空间通道的全连接层获得所提取的空间特征f2(Pn)∈RK×1(其维数与光谱通道相同)。
空-谱特征融合 为了利用光谱和空间特征融合改善高光谱图像分类的性能,将所提取的光谱特征f1(sn)与空间特征f2(Pn)传入MCB层,以此来获得多模态联合特征向量Φ(f1(sn),f2(Pn))∈Rd×1,其中d≪K2;由于MCB采用外积的计算概念,编码了f1(sn)和f2(Pn)特征向量中每个元素之间的相互关系,故而所产生的多模态联合特征向量比其他特征结合方式(比如级联)更具有表达性;此外MCB将f1(sn)和f2(Pn)特征向量投射到频域空间,避免对外积的直接计算,其有效解决了原双线性池化维数较高K2、计算复杂、容易产生过拟合等问题。最后,将所提取的多模态联合特征Φ(f1(sn),f2(Pn))传入顶端softmax线性分类器对每个像元进行分类。
2 基于多模态压缩双线性池化的空-谱特征融合
空-谱融合网络结构提取空-谱特征用于高光谱图像分类可由{f1(sn),f2(Pn),Φ,C}四部分组成,分别对应于双通道网络所提取的光谱特征、空间特征、空-谱联合特征及分类函数。如何有效地将空-谱不同模态特征融合为单一特征Φ表示对从高光谱数据特点的角度研究高光谱分类具有重要价值。
2.1 双线性池化
Tenenbaum等[18]采用双线性池化模型探究图片内容与图片风格之间的关系;Lin等[16]证明了双线性模型在细粒度分类应用中的有效性。双线性模型采用外积策略联合两个单一向量,若应用到本文来探究空-谱特征之间的关系,则有ΦBilinear(f1(sn),f2(Pn))=W[f1(sn)⊗f2(Pn)],其中⊗表示向量外积。这样,双线性模型允许空-谱向量的每一个元素以相乘的方式进行特征融合,能够充分探究空-谱特征之间的复杂关系;但双线性模型在带来特征高度融合性的同时,也带来了高维数的特征表示问题。在本文中,经过双通道特征提取以后,所得到的光谱和空间特征分别为f1(sn)∈RK×1,f2(Pn)∈RK×1,文中取K=512,则f1(sn)⊗f2(Pn)∈R512×512,经过线性运算,所需学习的权值W∈R512×512。这样的高维数参数学习与高光谱图像可利用标签数据较少之间是矛盾的,极易引起过拟合问题,同时也带来了高的计算花费。
根据以上分析,急需一种解决方案将向量的外积投射到低维空间中,避免对外积的直接计算。Gao等[17]在单一模态下提出压缩双线性池化,其利用Tensor Sketching算法的低维嵌入来近似表示同一模态的双线性特征。本文在此基础上,将压缩双线性池化推广到多模态条件下,用以探究高光谱图像的空-谱特征融合。
2.2 多模态压缩双线性池化方法
受压缩双线性池化的启发,MCB采用Count Sketch投射函数Ψ,将空-谱特征向量的外积f1(sn)⊗f2(Pn)投射到低维空间表示为Ψ(f1(sn)⊗f2(Pn),h,g)(其中h,g为哈希映射),用来解决双线性模型维数过高、计算不灵活问题。而Pham等[19]曾解释两个向量外积的Count Sketch可表示为各自Count Sketch的卷积,则
Ψ(f1(sn)⊗f2(Pn),h,g)=Ψ(f1(sn),h1,g1)*
Ψ(f2(Pn),h2,g2)
(1)
其中*表示卷积运算;故上述求解空-谱联合特征的过程可转化为f1(sn),f2(Pn)∈RK×1两个特征向量分别使用Count Sketch函数Ψ投射为f1′(sn),f2′(Pn)∈Rd×1以便近似计算空-谱多模态双线性特征。具体过程如下。
首先,随机初始化两个向量hk∈{1,2,…,d}K,gk∈{-1,1}K,其中k=1,2,hk将输入向量fk(·)的每一个索引i映射到输出向量的索引j∈{1,2,…,d},即j=hk[i];对于输入向量的每一个索引i,gk[i]为1或-1;同时,hk在{1,2,…,d}及gk在{-1,1}上都是服从均匀分布的。其次,对于输出向量的索引j所对应的值存在关系fk′(·)[j]=fk′(·)[hk[i]]=∑gk[i]·fk(·)[i],i=1,2,…,K。这样f1′(sn),f2′(Pn)∈Rd×1即为通过Count Sketch投射函数Ψ作用获得的输出向量。
此外根据卷积定理可知,时域中的卷积对应于频域中的乘积。故式(1)又可以表达为:
Ψ(f1(sn)⊗f2(Pn),h,g)=FFT-1(FFT(f1′(sn))⊙
f2′(Pn))
(2)
即
Φ(f1(sn),f2(Pn))=FFT-1(FFT(f1′(sn))⊙f2′(Pn))
(3)
其中:⊙表示点积运算;Φ(f1(sn),f2(Pn))为最终获得的空-谱特联合征向量。多模态压缩双线性算法的伪代码为:
输入:光谱特征向量f1(sn)∈RK×1,空间特征向量f2(Pn)∈RK×1。
输出:空-谱联合特征向量Φ(f1(sn),f2(Pn))∈Rd×1。
Fork=1,2
Fori=1,2,…,K
hk[i]将i均匀映射到{1,2,…,d}
gk[i]将i均匀映射到{-1,1}
End
Fori=1,2,…,K
j=hk[i]
fk′(·)[j]=fk′(·)[hk[i]]=∑gk[i].fk(·)[i],i=1,2,…,K
End
返回结果fk′(·)=Ψ(fk(·))
End
返回Φ(f1(sn),f2(Pn))=FFT-1(FFT(f1′(sn))⊙f2′(Pn))
多模态压缩双线性池化能够被嵌入到双通道特征提取网络中进行端到端的训练,本节将介绍其在网络中反向传播的过程。
假设损失函数为Loss,则根据式(1)可知MCB的反向传播能够表示为:
(4)
(5)
(6)
(7)
其中,i=1,2,…,K,由于hk仅是关于向量索引的映射,故而在反向传播过程中,仅需计算gk,k=1,2的梯度即可。
3 实验结果与分析
本文实验使用Indian Pines和University of Pavia两个高光谱数据集来验证本文所提出的算法的有效性。Indian Pines数据集为航空可见红外成像光谱仪 (Airborne Visible Infrared Imaging Spectrometer, AVIRIS) 于1992年采集得到的高光谱图像,其包含220个波段(波长范围为0.4~2.5 μm),有16种主要地物,图像大小为145像素×145像素,空间分辨率为20 m,去除其中20个噪声严重的波段(104~108,150~163,220),得到包含200个光谱波段的数据。图2(a)、(b)为原始Indian Pines数据集对应的假彩色影像和标记模板。University of Pavia数据集为反射光学系统成像光谱仪(Reflective Optics System Imaging Spectrometer, ROSIS)采集得到的高光谱数据,其包含115个波段(波长范围为0.43~0.86 μm),含9种主要地物,图像大小为610像素×340像素,空间分辨率为1.3 m,去除其中噪声严重的12个波段,剩余103个光谱波段的数据用来分类。图3(a)、(b)为University of Pavia数据集对应的假彩色影像和标记模板。本文实验基于Caffe框架[20],显卡为GTX860 4 GB的PC。
为了评价文中所提出算法的分类精度,本实验将其与最新的基于深度学习的高光谱图像分类方法:CNN[12]、Bi-CLSTM[13]及以级联方式结合空-谱特征的Two-CNN[14]方法进行对比。Indian Pines和University of Pavia数据集被随机分为:10%为训练集,10%验证集及80%测试集。同时,采用总体分类精度(Overall Accuracy, OA),平均分类精度(Average Accuracy, AA),Kappa系数及每一类的分类精度来评估模型的性能。
实验中空-谱融合网络(SSF-Net)模型各层参数如表1所示。本实验中通过随机梯度下降法对Two-CNN及SSF-Net进行训练,使用Salinas Valley数据集对网络进行微调,利用“多步”(multistep)策略调整学习率,初始学习率权重base_lr为0.000 1,调整系数gamma为0.8,最大迭代次数max_iter为100 000。
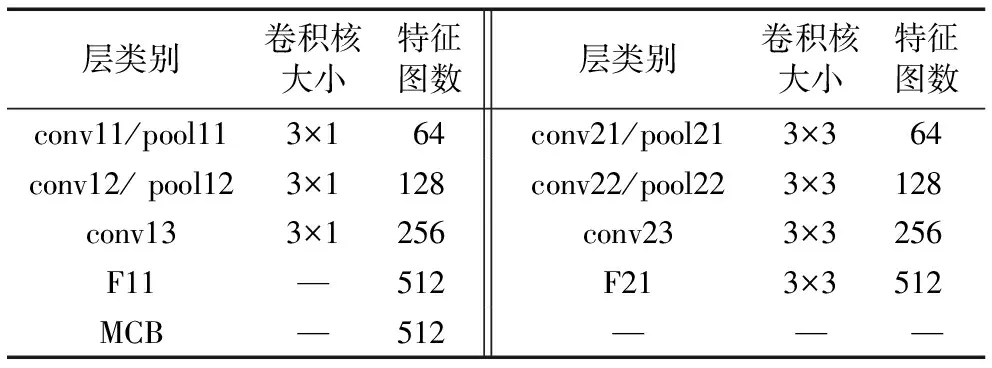
表1 SSF-Net网络参数设置
CNN、Bi-CLSTM、Two-CNN及本文所提出的SSF-Net在Indian Pines和University of Pavia数据集上的分类准确率如表2所示,其对应的分类效果如图2~3所示。表2最后一列的加粗数据为本文算法所改善的分类精度,从SSF-Net与其他深度学习方法的分类精度对比情况可以看出,SSF-Net相比CNN、Bi-CLSTM高光谱分类算法,OA、AA、Kappa等分类精度得到了明显提高(提高2个百分点左右);与Two-CNN的分类效果相比,SSF-Net的OA、AA、Kappa精度提高2~3.5个百分点,说明了相比简单特征级联,MCB所获得的空-谱联合特征能够更充分捕捉空-谱特征之间的复杂关系,有助于高光谱分类性能的提高。而从图2~3的分类效果中可以看出,基于MCB的双通道网络所产生的分类效果图噪点更少,即错分类的样本点更少,如图2(f)相比图2(e),把Grass-pasture错分为Corn-notill的像素点更少。

图2 Indian Pines数据集分类效果
为了探究MCB层投射维数对SSF-Net网络性能的影响,本部分将在数据集Indian Pines上,比较投射维度d对OA、AA、Kappa分类精度的作用,如图4所示。文中F11和F21层的维数为512,从图4可以看出,当MCB层维数从128到512时,OA增加1%的精度,相较维数从512增加至1 024时OA值增加要快,但维数低于512时,高光谱分类的AA值较低,表明少部分类别错误分类较多;虽然维数为1 024时分类性能要好于维数为512的网络,但增加维数的同时也增加了计算量,精度提升并不明显。相比较而言,当双通道各自提取的特征维度为512时,MCB层取维数为512最合适。

图3 University of Pavia数据集分类效果
表2使用不同方法在两个数据集上的分类结果对比%
Tab. 2 Classification results on two data sets using different methods %
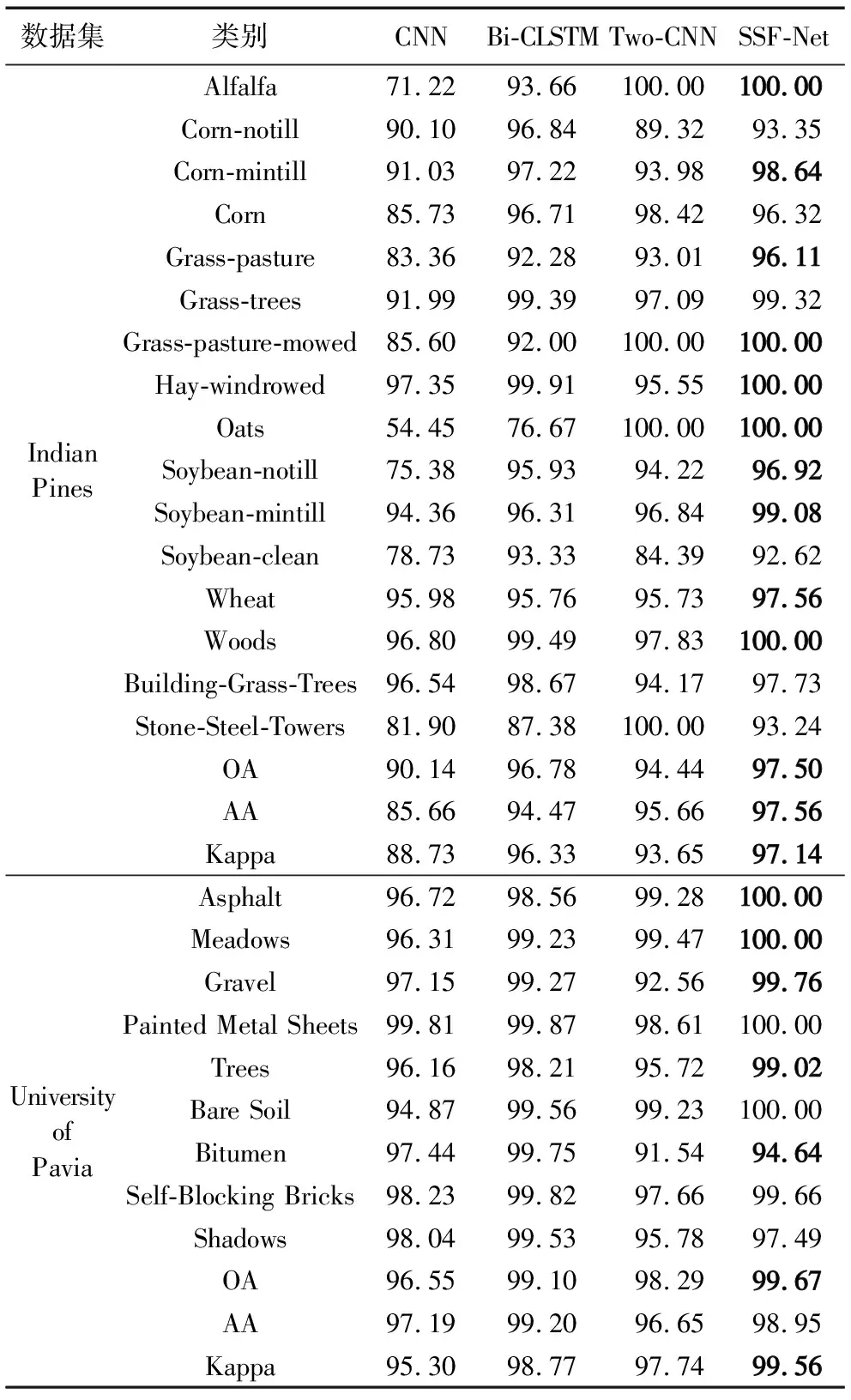
数据集类别CNNBi-CLSTMTwo-CNNSSF-NetIndian PinesUniversityof PaviaAlfalfa71.2293.66100.00100.00Corn-notill90.1096.8489.3293.35Corn-mintill91.0397.2293.9898.64Corn85.7396.7198.4296.32Grass-pasture83.3692.2893.0196.11Grass-trees91.9999.3997.0999.32Grass-pasture-mowed85.6092.00100.00100.00Hay-windrowed97.3599.9195.55100.00Oats54.4576.67100.00100.00Soybean-notill75.3895.9394.2296.92Soybean-mintill94.3696.3196.8499.08Soybean-clean78.7393.3384.3992.62Wheat95.9895.7695.7397.56Woods96.8099.4997.83100.00Building-Grass-Trees96.5498.6794.1797.73Stone-Steel-Towers81.9087.38100.0093.24OA90.1496.7894.4497.50AA85.6694.4795.6697.56Kappa88.7396.3393.6597.14Asphalt96.7298.5699.28100.00Meadows96.3199.2399.47100.00Gravel97.1599.2792.5699.76Painted Metal Sheets99.8199.8798.61100.00Trees96.1698.2195.7299.02Bare Soil94.8799.5699.23100.00Bitumen97.4499.7591.5494.64Self-Blocking Bricks98.2399.8297.6699.66Shadows98.0499.5395.7897.49OA96.5599.1098.2999.67AA97.1999.2096.6598.95Kappa95.3098.7797.7499.56
4 结语
针对空-谱特征简单结合产生维数过高及联合特征表达能力较弱的问题,本文提出一种基于空-谱融合网络的高光谱图像分类方法。该方法以空-谱信息为基础,探究双通道特征提取网络的特征融合方法。为了分析空-谱特征之间的关系,采用双线性模型的外积计算策略寻找光谱和空间特征向量中各元素之间的复杂联系。考虑直接外积计算会带来维数灾难,导致网络过拟合问题,文中提出多模态压缩双线性池化方法,将原特征向量的外积投射到低维空间中,转换为傅里叶空间频域中的点积运算。该方法既可以汲取双线性模型能够对光谱和空间特征向量中的每一个元素进行融合的特点,也避免了双线性模型直接外积运算带来的高维数、高计算消耗的问题。同时,实验也验证了MCB所获得的空-谱联合特征更有助于改善高光谱图像的分类性能。考虑本文在提取高光谱的空间信息时,对光谱通道进行了降维,这损失了一部分高光谱特征,未来将从降低光谱通道降维带来特征损失这一角度出发,对高光谱图像特征提取方法进行研究。
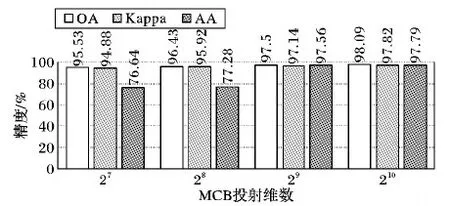
图4 MCB层维数对分类精度的影响

