一种新型反双曲正弦函数跟踪微分器设计
李兴格,李 刚,熊思宇,康旭超
(1.空军工程大学 研究生院, 西安 710051; 2.空军工程大学 防空反导学院, 西安 710051)
在控制系统的设计中,准确提取微分信号非常重要[1]。特别是当系统存在外部干扰时,传统的低通滤波器很难发挥作用。近年来,随着机器人[2-3],高超声速飞行器[4-5]等领域的迅速崛起,从干扰信号中提取精确的微分信号已成为研究的热点。
跟踪微分器最初由韩京清[6-8]提出。提出了3种跟踪微分器,但跟踪微分的效果不是很好,且没有更好的方法来解决高阶微分信号的提取问题。近年来,许多学者提出了许多种新型的跟踪微分器[9-12]。以色列学者Levent针对高阶微分问题提出了一种高阶滑模微分器[13]。然而,由于此微分器对噪声非常敏感,并且难以选择参数。因此,设计一种参数选择比较简单且具有噪声抑制能力的跟踪微分器显得十分必要。
基于以上考虑,本文提出了一种基于反双曲正弦函数的跟踪微分器,并且在前人的基础上,减少了跟踪微分器的整定参数,提高了跟踪微分器的可操作性。
1 跟踪微分器设计
在常规状态下,跟踪微分器需要满足以下两个条件以实现对受干扰的微分信号的稳定跟踪。首先,在零点附近的线性区域下具有平滑稳定的线性特性,在远离零点的非线性区域中,需要具有非线性特性以确保跟踪微分器的稳定跟踪。 因此,选择反双曲正弦函数作为跟踪微分器的加速度函数。
1.1 二阶跟踪函数设计
定理1对于以下系统
(1)
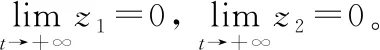
证明选择李雅普诺夫函数
(2)
由于a1>0,并且当z1>0时,a1arsinh(ξ)>0;当z1<0时,a1arsinh(ξ)<0。根据积分中值定理,可以得到
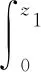
(3)
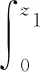
对其求导数,有
z2[-a1arsinh(z1)-a2arsinh(z2)]=
-z2a2arsinh(z2)
(4)
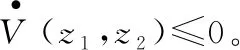
1.2 跟踪微分器设计
定理2对于以下系统
(5)
其中,系统的输入信号为u(t);x1(t)为系统的跟踪信号;x2(t)为系统的微分信号;R>0,a1>0,a2>0为系统的可调参数。
为证明定理2,先提出以下引理:
引理1[7]对于以下系统
(6)
若对于所有的解满足y1(t) →0,y2(t) →0(t→0)时,则对于任意常数T>0和任意的有界可积函数u(t),系统
(7)
的解x1(t)满足
(8)
该引理保证了系统在任意常数T的条件下,当R趋近于无穷大时,系统的跟踪信号x1(t)无限接近于系统的输入信号v(t)。因此,定理2提出的系统即为本文提出的新型跟踪微分器NATD。
2 相平面分析
应用相平面分析法不仅可以自动准确地绘制控制系统的相平面图[14-15],而且可以快速分析系统参数对控制系统的影响,从而研究系统参数的设置规则,对跟踪微分器的性能提升有很大的作用。
系统式(1)在零点的雅可比矩阵为
(9)
将系统式(5)中的x1使用泰勒公式展开,可以得到
(10)
将系统式(5)中的x2使用泰勒公式展开,可以得到
(11)
其中,φ和ψ为泰勒展开式的高阶无穷小项,则对系统(6)可以线性化为
(12)
对于近似线性系统式(12),矩阵A的特征值为
由相平面分析可知,系统式(5)包含3个参数:R,a1,a2,其中,R与跟踪效果有关,增大R可以提高跟踪速度,但会提高微分信号的高频噪声。a1的效果与跟踪效果有关,其效果与R类似;a2与微分效应有关,提高a2有利于抑制微分噪声,但是会使跟踪速度变慢。通常在进行参数整定时,可以粗略地选择R以调整跟踪效果。然后,通过a1和a2的微调来调整跟踪和微分的综合效果,最后使跟踪微分器达到最佳效果。与其他文献中提到的跟踪微分器相比,NATD的参数比较少,参数整定比较简单。
3 仿真验证
为了验证NATD的估计结果,将NATD与以下新的TD[16]和HSMD[13]进行比较。采用四阶Runge-Kutta法进行仿真求解,仿真步长为0.001 s。仿真在以下两种情况下进行。
情形1:在无噪声干扰的情况下,选择输入信号为υ(t)=sin(2πt),NATD和其他2个跟踪微分器选择的参数如表1所示,仿真结果如图1所示。
3个微分器的估计效果和微分效果如图1~图4所示。图2和图4显示,在3个微分器中,NATD的估计误差最小,精度最高。从图4可以看出,TD具有严重的峰值现象,HSMD在0附近有严重的抖振现象。因此,当不考虑噪声时,本文提出的NATD 与TD和HSMD相比具有一定的优势。

表1 无干扰情况下选择的参数
情形2:在有噪声干扰的情况下,输入信号υ(t)=sin(2πt),输入信号受到的干扰为均值为0,方差为0.1的高斯白噪声。跟踪微分器的参数选择如表2所示,仿真结果如图5所示。
由仿真结果图5~图8可知,当输入信号受到噪声污染时, NATD仍然可以实现对于输入的估计信号和微分信号的高精度和平滑估计。因此,与TD和HSMD等微分器相比,本文提出的NATD在噪声滤波方面也具有一定的优势。

表2 有噪声干扰情况下的参数选择
4 结论
设计了一种基于反双曲正弦函数的结构比较简单,并且在全局是渐进稳定的新型跟踪微分器。通过相平面分析适当调节参数,可以保证系统的奇点类型为稳定节点。既可以保证在零点附近有明显的线性特性,又能保证远离零点时的强非线性特性。仿真结果表明:NATD在跟踪精度,响应时间和滤波性能等方面也具有一定的优势。

