水声通信时延下集群式AUV分群控制算法
杨盼盼,张瑾琪,刘家毓
(长安大学 电子与控制工程学院, 西安 710064)
水下航行器群在海洋环境监测、水底测绘、搜索搜救等领域得到了日益广泛的应用,集群式AUV的协同控制已成为海洋工程的研究热点[1]。一般来讲,AUV的协同行为分两种:组群和分群[2]。组群要求在一定区域内随机分布的AUV能聚集在一起,并以编队形式协调地执行任务;与组群相反,分群表征为AUV群集在外部刺激下自发分裂为若干个子群的行为。目前以编队控制为代表的组群行为的研究是热点,但对于其分群行为的研究,尚处于十分欠缺的阶段。
AUV集群中个体的感知、计算、通信等能力通常十分有限,仅能依靠周围邻居的运动状态对自身行为进行调节。不同于基于统一中心协调控制[3]或依赖于指派[4]、协商[5]等智能化的分群方式,这类群集系统的分群行为,表征为无中心控制下个体仅通过局部交互而涌现出的一种自发应激反应。与传统的分群方法相比,这种分群方式在机理上有本质的不同,也更具难度。
雷小康等[6]提出了一种基于邻域跟随行为的分群控制方法,实现了无中心控制下群集系统的自组织应激分群。Liu等[7]利用AUV间耦合强度不同可导致群集分裂的特性,提出了一种基于信息耦合度的AUV分群控制方法。由于声音在水中的传播速度仅为1 500 m/s左右,远远小于空中电磁波的传播速度,对于依赖于水声通信进行信息交互的集群式AUV而言,通信时延是群集协同中不可忽略的问题[8]。时延的存在阻碍了邻居运动信息获取的实时性,降低了分群性能,增加了分群不确定性,甚至会导致分群算法失效。
本文针对水声通信时延下集群式AUV的分群控制问题,提出了一种基于信息耦合度的分群控制方法。通过建立AUV间的信息耦合度动态调节交互作用强度,实现在外部刺激下对AUV运动行为趋向性控制,达到了自发分群的目的。理论分析表明该算法在水声通信时延下的稳定性,仿真结果亦验证了该方法的有效性。
1 问题描述
1.1 AUV群集系统模型
对于在水下三维空间运行的N个AUV组成的群集系统,其个体动力学方程可描述为:
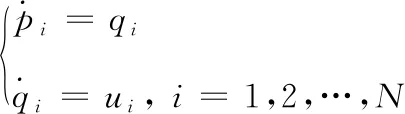
(1)
式(1)中,pi,qi∈R3分别为AUVi的位置和速度向量,ui∈R3为其加速度向量,在此作为控制输入。对应的邻居集Ni可表示为:
Ni={j|||pi-pj||≤R,j=1,2,…,N,j≠i}
(2)
式(2)中,R>0为AUVi的通信半径;||pi-pj||为AUVi和j之间的欧氏距离。
若将每一个AUV看作一个节点,则AUV群集中个体间的相互作用关系可用邻接图G=(V,E,A)来表示。其中,V={n1,n2,…,nN}表示顶点集,E={(ni,nj)∈V×V}为边集,(ni,nj)∈E表示AUVi与j互为邻居;A=[aij]为图G的邻接矩阵。对于一个无向图G,其邻接矩阵A为对称矩阵,且对应的Laplacian矩阵L为
L=D-A
(3)

1.2 水声通信时延模型
AUV群集系统中个体信息交互由水声探测网络和水声通信网络两部分组成,存在探测时延τmea和通信时延τcom两种时延形式[9],分别表示为:
τmea=τα+τc
(4)
τcom=τα+τβ
(5)
式(4)、(5)中,τα为声波在水中的传播时延;τc为量测过程中的处理时延;τβ为水声通信非传播时延部分,包括通信包的发送、接收及处理时延等。
由于水声通信过程中信号处理的高复杂性及水下环境中的带宽受限,传播速率低等原因,通常通信时延明显长于同等距离的声纳探测时延。因此,本文做出如下假设:
假设1AUV的探测时延远小于通信时延(即τmea≪τcom),可以忽略,本文仅研究存在通信时延的情形。
假设2AUV群集的通信时延为均匀时延(uniform delay),个体间的时延相等且为定值,即τ12=τ13=…=τ21=τ23=…τnm=τ。
基于上述假设,本文拟在AUV间信息交互存在时延的情况下,通过设计分布式分群控制算法,使AUV群集系统能在外部刺激作用下,不借助于任何集中控制方法或指派、协商等智能化方式自发分裂成若干子群,同时,分出的子群能保持有序性,以编队的形式正常运行。
2 水声通信时延下的分群控制算法
2.1 基于信息耦合度的分群策略
信息耦合度表征AUV间的交互作用强度,可用于对个体的运动趋向性进行调节,在分群过程中起关键作用[7]。本文借鉴生物个体分群运动中对周围邻居运动状态变化敏感的特性,基于AUV间的相对位置信息,构建如下信息耦合度函数:
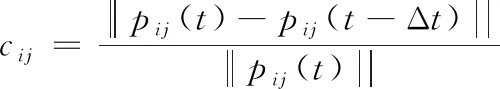
j∈Ni(t)∩Ni(t-Δt)
(6)
式(6)中,pij(t)=pi(t)-pj(t)和pij(t-Δt)=pi(t-Δt)-pj(t-Δt)分别为t时刻和t-Δt时刻AUVi和j之间的相对距离;Δt为两次通信的时间间隔。
分群行为的实质是多元外部刺激信息在群集中传播所引起的一种个体运动行为分化现象。当外部刺激导致个体运动行为出现冲突时,通过选择机制可使个体对信息冲突进行消解,从而在群体层面上涌现出一种分裂现象[10]。
基于上述思想,在分群过程中选择AUVi邻域内信息耦合度最大的个体fi作为对其运动影响最大的个体,可表示为:
(7)
式(7)中,c*>0为分群阈值。
2.2 水声通信时延下基于信息耦合度的分群控制算法
基于式(7)中所确定的最大信息耦合度邻居fi,通过将其运动信息融入AUVi的协同控制律中,可将AUV分群控制算法设计为:
k1(pi-pfi)-k2(qi-qfi)-giei
(8)
可见,分群控制律由三部分组成,其中:
(9)
式(9)中,A为人工势场强度系数,B为其结构系数,pfij=pfi-pfj为AUVi与j邻域内最大信息耦合度个体fi和fj间的相对位置信息。
3) -k1(pi-pfi)-k2(qi-qfi)为融合邻域内最大信息耦合度个体运动信息的分群项,具有引导分群的作用。在此,k1,k2>0为反馈增益系数,pfi和qfi分别是AUVi邻域内最大信息耦合度个体的位置和速度信息。
4) -giei为外部刺激信号,是导致群集运动行为分化的诱因。在此,用gi=1表示第i个AUV能感知到外部刺激,反之gi=0。
(10)
(11)
根据式(11)中设计的分群控制律,有如下定理:
定理1对于由式(1)描述的集群式AUV系统,假设个体间信息交互存在水声通信时延τ,当外部刺激导致群集中部分个体运动行为冲突时,在分群控制律式(11)的作用下,AUV群集能自发分裂成若干子群,且子群中AUV的速度与子群中最大信息耦合度个体的速度趋于一致。
2.3 分群稳定性分析
选取如下半正定Lyapunov函数:
(12)
对式(12)沿时间求导,有:
(13)
根据邻接矩阵A和人工势场函数ψij的对称性[12],有:
(14)
因此,
(15)
将式(15)代入式(13)中,可得:
(16)
从式(16)可知,Q是一个非增函数。假设所选取的子群初始能量Q0为有限值,则对于任意时间t,Q (17) qi=qfi (18) 即AUVi的速度最终会与其邻域内最大信息耦合度个体fi的速度趋于一致。 假设第Ni个AUV为子群中接收外部刺激信号的个体,根据式(6)可知,子群中接受外部刺激信号并导致速度突变的个体为子群中信息耦合度最大的个体。在有限时间段t~t+Δt内,总存在一条路径使个体i与子群中速度突变个体fNi保持连通,即两者之间存在一条联合路径,在所设计的分群算法下子群中所有个体的速度最终会与速度突变个体fNi的速度趋于一致,即 q1=q2=…=qNi-1=qNi (19) 式(19)中,qNi是子群中感知外部刺激并做出机动运行的个体fNi的速度。 为验证本文所提水声通信实验下集群式AUV分群控制算法的可行性和有效性,选取30个AUV组成的群集在Matlab下展开仿真研究。 假设AUV初始状态下随机分布在15 m×15 m矩形区域,通信半径R=5 m,时延τ=0.1 s。其他仿真参数分别为:c*=0.3,Δt=0.05 s,A=10,B=5,k1=k2=1。 在t=6 s时刻外部刺激施加在群中的两个AUV上,使其分别以[8 0]Tm/s[0 8]Tm/s的速度向不同方向运动。在分群控制算法(10)的作用下,AUV群集开始实施分群运动。仿真结果如图1、2所示。 从图1可以看出,在初始状态下随机分布的AUV首先向中心聚集并以编队的形式协同运动,在群内两个AUV感受到外部刺激向不同方向运动时,其余AUV在分群控制算法的作用下,根据最大信息耦合度邻居调整自身运动,最终分裂成两个独立运行的子群。 从图2可以看出,AUV速度首先从随机状态趋于一致;在外部刺激施加在两个AUV上后,AUV群集的速度出现分化,分别趋向于感受到外部刺激的AUV的速度,最终实现群集的稳定分裂运动。 通过利用AUV间的信息耦合度动态调节交互作用强度,实现了水声通信时延下AUV群集的自组织分裂。理论分析表明该算法的稳定性,仿真结果验证了该方法的有效性。
3 仿真结果及分析
4 结论

