基于最小二乘支持向量机的氧化铝浓度预测
崔家瑞,张政伟,李 擎,崔家山
(北京科技大学, 北京 100083)
在电解铝的生产过程中,氧化铝浓度是决定其生产过程各项技术指标的关键参数,当电解质的氧化铝浓度过高,继续下料添加氧化铝会造成氧化铝原料在电解槽槽底沉淀,电阻增大,电流效率变低,影响铝电解的正常生产,氧化铝浓度过低时,电解槽又会发生阳极效应,槽电压剧烈上升,电解槽的能量平衡被破坏,降低出铝量[1]。因此,为保证电解槽高效生产,必须严格控制电解槽内氧化铝浓度在1.5%~3.5%范围内[2]。
曹阿林等[3]通过确定铝电解槽电压与氧化铝浓度间的关联关系,并绘制出铝电解槽的控制曲线,为实现铝电解过程中氧化铝浓度的控制提供理论依据;林景栋等[4]针对铝电解过程氧化铝浓度判断困难的问题,提出基于线性回归预测与正交变换预测法,给出槽电压、电解槽状态和出入量三个输入量来预测氧化铝浓度;张瑜等[5]釆用软测量技术来估计氧化铝浓度,运用径向基函数神经网络构建软测量的数学模型估计出氧化铝浓度,从而实现氧化铝浓度的在线检测;吕函珂等[6]综合利用模糊解耦、模糊推理方法,根据槽电压判定当前浓度值,同时建立氧化铝浓度正交变换预测判定模型;张森等[7]利用阳极导杆电流和两极压降运用ELM算法成功预测了氧化铝浓度,但这些方法预测的氧化铝浓度误差依旧较大,因此如何提高测量精度依旧是一个重要的研究方向。
在国家863项目《铝电解生产在线检测与MES系统关键技术研究及应用》基础上,利用现场一组导杆采集到的100组数据,研究了如何实现氧化铝浓度的在线测量。
1 软测量依据
铝电解过程中可直接采集的数据主要有槽电压、下料间隔、槽电阻、温度等,这些参数都对电解槽氧化铝浓度有一定影响,然而最直接、最快速的参数还是槽电阻。
1.1 槽电阻
槽电阻和氧化铝浓度之间存在某中“U”型关系[8],如图1所示,由此在生产过程中可以通过观测槽电阻来获得氧化铝浓度的相关信息。
图1将槽电阻与氧化铝浓度的对应关系分为4个区:高含量区:电阻对浓度变化十分敏感,但氧化铝浓度过高会造成槽底沉淀;不敏感区:电阻对含量的变化不敏感,电流效率低;可控制区:电阻对浓度变化较为敏感,而且电流效率较高,工业氧化铝浓度理想控制区;多效应区:氧化铝含量很低,随氧化铝浓度下降电阻急速升高,极易出现阳极效应现象。
在铝电解过程中,尽量把浓度控制在可控制区,通过测量槽电阻,依据槽电阻和氧化铝浓度的关系,达到间接测量氧化铝浓度的目的。
广义上来讲,电解槽的槽电阻可以从整体的角度得到:
(1)
式(1)中:Ri为第i时刻铝电解槽的槽电阻(mΩ);Ui为第i时刻铝电解槽的槽电压(V);Ii为第i时刻铝电解槽的系列电流(kA);B为表观反电动势,通常都看做一个固定的值,但由于每个铝电解厂的电解槽结构或者系列电流不同,会造成表观槽电阻略有不同,其值一般在1.6~1.7 V之间波动。
1.2 阳极导杆电流
阳极导杆电流能够直接反映电解槽内部阻抗,即与氧化铝浓度和极距均有一定的关系。由于每根阳极导杆的电流在6~8 kA左右,无法直接在线测量,针对此问题,采用等距压降法测量阳极导杆电流。
等距压降法测量电流就是在阳极导杆上选取一段固定的导杆,采用硬件设备测量该段导杆的电压值,然后采用欧姆定律计算电流[9]。即:
在电解过程中,阳极导杆的温度是实时变化的,这就导致了阳极导杆电阻率的变化,阳极导杆实际电阻为
(2)
式(2)中:α为电阻率温度系数;ρ为电阻率;L为等距压降测量点之间的距离;S为阳极导杆横截面积;T为导杆测点表面的温度。
1.3 两极电压
两极电压是指阳极导杆夹具触点到阴极钢棒之间的电位差,比槽电压更能快速反应各阳极导杆下的氧化铝浓度变化情况,如图2所示。
槽电压除了受电解槽本身槽况的影响之外,很大程度上还会受限于整流所提供的直流电,直流电会出现各种意外情况或者波动,造成槽电压的变化情况不能直观反映槽况。
因此,只需要测量阳极导杆电流和两极电压,即可借助槽电阻得到氧化铝浓度,并克服了槽电压波动的影响。
2 氧化铝浓度预测方法
由上一章可知,阳极导杆电流和两极电压与氧化铝浓度之间存在某种非线性关系,在数据波动较小的情况下,最小二乘支持向量机[10](英文名称,LSSVM)可以很好做出回归分析。因此,将阳极导杆电流和两极电压作为模型的输入,氧化铝浓度作为输出,可以建立与实际情况相符合的模型。
2.1 最小二乘支持向量机建模
利用在线监测终端同步采集阳极导杆电流和两极电压,与此同时,通过人工采集氧化铝,并在实验室离线测量,得到氧化铝浓度。最后,通过将阳极导杆电流、两极电压与离线氧化铝浓度对标,得到了100组有效数据。采集装置如图3所示。
由于采集的阳极导杆电流、两极电压和氧化铝浓度数据之间存在不同的量纲,因此各类数据均需按下式对训练样本数据进行归一化处理:
由于导杆电流与氧化铝浓度存在一定的非线性,而最小二乘支持向量机可以很好解决非线性问题,因此,采用最小二乘支持向量机方法进行预测。
回归问题中,对于给定的n维输入t维输出的训练样本集D={(xi,yi),i=1,2,…,m},可以利用非线性映射到高维特征空间,即
(3)
根据结构风险最小化原理,将式(3)表示为一个等式约束的优化问题:
(4)
式(4)中:J(ωj,eij)为结构风险函数;eij为模型预测值和真实值之差;γ为惩罚因子。
为了求解上述问题,需要将此约束问题转换为无约束优化问题,为此需要引入拉格朗日乘子向量,建立拉格朗日等式方程,优化问题变为
L(ωj,bj,αij,eij)=J(ωj,eij)-
(5)
根据最优化理论的KKT条件,分别对式(5)中的(ωi,bj,eij,αij)求偏导,转化为求解方程:

(6)
消去ω和eij,式(6)重写为
(7)
式(7)中,K(·,·)是核函数,满足Mercer条件
K(xi,xj)=φ(xi)φ(xj)
求解式(7)方程组,得到最小二乘支持向量机(LSSVM)模型为
综上,将归一化后的阳极导杆电流和两极电压作为最小二乘支持向量机的输入,氧化铝浓度作为模型输出,进行训练。
2.2 模型参数寻优
对于最小二乘支持向量机而言,超参数的取值与学习数据样本集以及研究对象密切相关。惩罚因子γ值越大则允许的误差越小,越小则允许的误差变大。数据样本的输入范围很大,就需要增大核函数宽度σ2的取值:反之,则需要减小核宽度的取值。
LSSVM模型的性能选择取决于其核函数和2个超参数的选择。核函数选取RBF函数[11-12],取合适的惩罚因子γ和核函数宽度σ2,是建立最小二乘支持向量机预测模型的关键,采用网格搜索和交叉验证[13-15]的方法选择LSSVM参数。
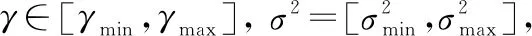
K折交叉验证的步骤:
① 不重复抽样将原始数据随机分为k份;
② 将其中k-1份数据集用于训练,剩下的1份用于测试;
③ 重复第二步k次,在每个训练集上训练后得到一个模型,用这个模型在相应的测试集上测试,计算并保存模型的评估指标;
④ 计算k组测试结果的标准差作为模型精度的估计,并作为当前k折交叉验证下模型的性能指标。
3 仿真实验
对贵州某现场230 kA预焙阳极1号车间A1导杆测量采集100组数据,进行归一化处理,利用Matlab 2013软件进行编程,将100组数据采用LSSVM算法进行建模,核函数采用径向基核,由网格搜索(γ和σ2有35组参数组合)和交叉验证验证(80组数据进行训练,20组数据进行验证)方法得到氧化铝浓度预测的标准差如图4所示。
由图4可知,γ和σ2的参数组合在第19组氧化铝浓度预测值标准差最小,RMSE=0.132 1,得出该出惩罚因子为γ=10,核函数σ2=1。
模型参数确定(γ=10,σ2=1)后,得出在该组参数下训练的各个样本集的结果,分别如图5和图6所示。
由图5可知,算法模型能够很好地拟合实际生产数据;由图6可知,氧化铝浓度整体平均相对误差为0.051 2,个体相对误差大都在0.05附近。
采用平均相对误差和均方根误差作为评价标准,平均相对误差计算公式为
均方根误差RMSE计算公式为
其中N为测试样本个数;y为真实值;yi为模型输出值。
将仿真结果与文献[5]的ELM算法进行比较,仿真结果如表1所示。

表1 算法性能比较
由表1可知,本文所提方法与文献[5]相比,在RMSE保持基本不变的基础上,整体平均误差降低了22%,测量精度得到了进一步提高。
4 结论
提出了一种基于最小二乘支持向量机回归模型的氧化铝浓度软测量方法。该方法将易在线测量的阳极导杆电流、两极电压作为模型输入,采用网格搜索和交叉验证的方法得到模型最优超参数,提升软测量精度;基于现场采集的数据,验证了所提方法的有效性。虽然所提方法能够实现氧化铝浓度的软测量,但在实际应用中还需进一步提高实时性和稳定性。

