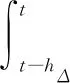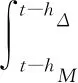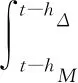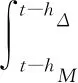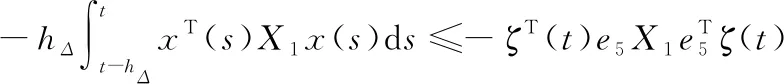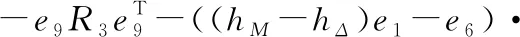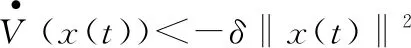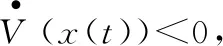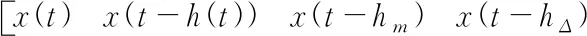区间变时滞系统的时滞相关鲁棒非脆弱H∞控制

左朝阳，吴玉彬，何 星,

(1.西京学院 机械工程学院， 西安 710123； 2.火箭军工程大学 控制工程系， 西安 710025)

现实世界的许多动力学模型系统，例如网络控制系统、过程控制系统以及核反应堆控制系统等，在数据和物质的传输过程中，都包含非常明显的时滞。在众多的时滞类型中，区间变时滞更具代表性，它的时滞下界不一定为零，且时滞处于一个变化的区间之内，常见于化学反应器、内燃机和网络控制等工程实际应用中。因而近年来，区间变时滞系统的稳定性分析成为一个热门的研究领域[1-29]。

针对区间时滞系统的稳定性分析,最常见的方法是采用基于时域内直接构造(L-K)泛函并结合线性矩阵不等式(LMI)来实现；针对其镇定问题，一般采用状态反馈的形式来实现。文献[2-9]讨论了在状态反馈控制器作用下系统的镇定问题，但所给出的控制器无论是无记忆或者有记忆还是H∞控制器，都要求能够精确实现，不具有鲁棒性。在控制器的设计实现中，由于硬件(如A/D、D/A转换)和软件(如计算截断误差)等原因，控制器不同程度上存在一定的不确定性[10]。Keel等[11]指出，当控制器参数存在摄动时，常规的鲁棒控制器表现出高度的脆弱性，从而造成闭环系统的性能下降甚至控制器失效。因此非脆弱控制器的研究便成为大家关注的热点问题[12-17]。文献[12-14]和文献[16-17]分别针对时滞系统的非脆弱H∞控制问题和非脆弱保性能控制问题进行了深入研究。在这些研究中，主要围绕如何降低所得结论的保守性和满足一定的性能指标而展开。由于时滞相关条件相比时滞无关条件具有更小的保守性，因此，如何选取合适的L-K泛函和界定条件，进一步得到保守性更小的时滞相关条件进而设计有效的控制器便成为目前时滞系统稳定性分析与控制综合的重点问题。

本文针对一类区间变时滞不确定系统，提出一个形式简单的保守性更低的时滞相关有界实判据。该判据借助于一种新型的时滞分割法，把时滞区间分割成不均匀的两部分，针对每一分割区间构造新的L-K泛函，并采用新的积分不等式和互凸组合技术给出不包含任何多余参量的LMI形式结论。在此基础上设计了鲁棒非脆弱控制器。最后把该控制器应用于VTOL直升机的飞行控制当中，仿真结论表明所推导的有界实判据相比已有文献结论具有更低的保守性，所设计的控制器相比一般鲁棒控制器具有更好的镇定效果和明显的非脆弱性。

1 问题描述

考虑如下一类具有区间变时滞的线性系统:

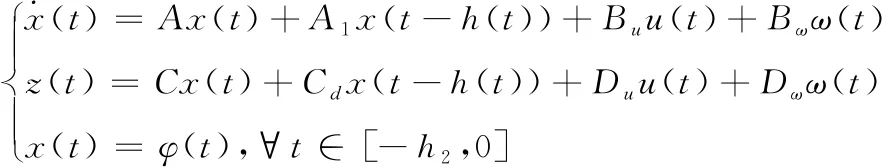
(1)

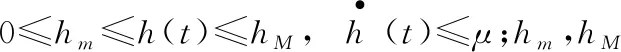
针对系统(1)定义如下性能指标

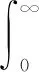
(2)

其中，γ>0为给定标量。

本文主要目标是在外部干扰作用下，设计一个状态反馈非脆弱H∞控制器：

u(t)=(K+ΔK)x(t)

(3)

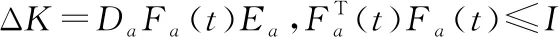
使得满足以下两个条件：

第一，ω(t)=0时，由(3)构成的闭环系统(1)渐近稳定；

第二，在零初始条件下，对于给定的γ>0， ||z(t)||2<γ2||ω(t)||有，ω(t)∈L2[0,∞)。

把非脆弱控制器(3)代入系统(1)，则闭环系统为：

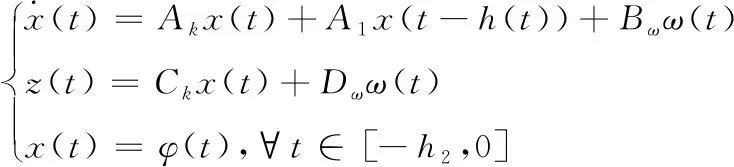
(4)

其中,Ak=A+BuK+BuΔK,Ck=C+DuK+DuΔK。

为了方便稳定性判据的证明，现将下一步需用到的引理归纳如下：

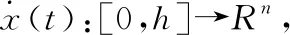
引理2[25]假定任意的正定矩阵M=MT>0，标量h>0和向量函数：x(t)∶[0,h]→Rn，则有以下不等式成立：

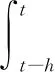
引理3[28]假定任意的正定矩阵M=MT>0，标量0≤α,ε≤1，hm≤h(t)≤hM和向量函数：x(t):[0,h]→Rn，则有以下不等式成立：

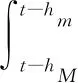
其中，

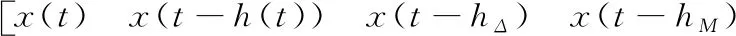
引理4[17]给定具有适当维数的矩Q=QT,H,E和R=RT，则有Q+HF(t)E+ETF(t)THT<0,对任意满足F(t)TF(t)≤R的F(t)成立的充要条件是存在ϑ>0,使得:

Q+ϑ-1HHT+ϑETE<0

2 时滞相关有界实判据

定理1对于给定的标量hm，hM和λ1，λ2(λ1>λ2)，且若存在正定对称矩阵Pi(i=1,2,3,4,5)，Q1，Q2，U1，U2，Xj，Rj(j=1,2,3,4)，使得如下LMIs成立：

Φ=(Φi, j)10×10<0

(5)

则系统(4)在非脆弱控制器(3)的作用下不仅渐近稳定，而且在零初始条件下具有给定的H∞扰动抑制水平γ。

其中

Φ=(Φi, j)10×10=

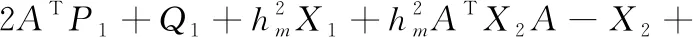
Φ13=X2，Φ15=2P2+hmR2

Φ16=(2-ε)(hM-hm)R4

Φ17=(1+ε)(hM-hm)R4

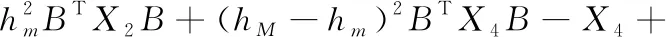
Φ23=-(α-2)X4，Φ24=(1+α)X4

Φ25=Φ26=Φ27=Φ28=Φ29=Φ210=0

Φ33=Q2-Q1-X2+(α-2)X4，Φ35=-2P2

Φ36=Φ37=2P3，Φ34=Φ38=Φ39=Φ310=0

Φ44=-Q2-(1+α)X4，Φ46=Φ47=-2P3

Φ45=Φ48=Φ49=Φ410=0，Φ55=-X1-R2

Φ58=-2P4，Φ56=Φ57=Φ59=Φ510=0

Φ66=(α-2)X3-(2-ε)R4，Φ69=Φ610=-2P5

Φ67=Φ68=0，Φ77=-(α+1)X3-(1+ε)R4

Φ79=Φ710=-2P5，Φ78=0，Φ88=-R1-U1

Φ89=Φ810=0，Φ99=-(2-ε)R3-U2

Φ910=-U2,Φ1010=(1+ε)R3-U2

证明：证明过程详见附录。

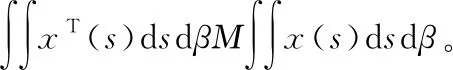
在式(5)中，新的稳定性判据没有涉及冗余的自由权矩阵，只是巧妙地采用新的积分不等式来界定LKF导数产生的交叉项，并利用极少数自由矩阵来表示相关项之间的关系，因此减少了理论推导和计算上的复杂性，从而降低了结论的保守性。

在式(10)、式(11)和式(14)中，互凸组合处理技术[22]作为一种非传统方法用来更有效地界定LKF导数产生的交叉项，可以得到保守性更低的稳定性结论。

3 非脆弱H∞控制器的设计

基于时滞相关有界实判据，设计非脆弱H∞控制器。

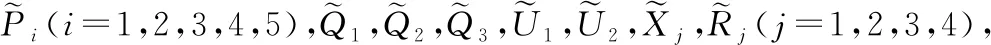
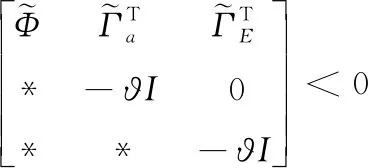
(31)

则不确定系统(1)在非脆弱控制器(3)的作用下不仅渐近稳定，而且在零初始条件下具有给定的H∞扰动抑制水平γ,且控制器增益K=YΞ-T。其中，

证明：由于定理1中式(5)给出的条件为非线性矩阵不等式,不能直接得到控制器的解。下面给出控制器的设计方法，首先将式(5)中的不确定项(即含ΔK项)分离，即

(32)

其中,Φ′为Φ中分离不确定项(含ΔK项)所得结果。由引理4可得

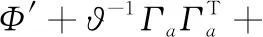
(33)

其中

进而对式(33)应用Schur补可得

(34)

令T1=T2=Ξ-1,其中Ξ为非奇异矩阵，对式(34)两边左乘Ψ，右乘其转置，其中：

通过替换容易得到定理2的条件，证毕。

4 数值仿真与比较

下面通过2个数值例子仿真来比较说明本文方法所提出时滞相关有界实判据和基于此设计的鲁棒非脆弱控制器都在不同程度改善了已有文献的结论。其中，MADB (Maximum Allowable Delay Bound) 定义为保证系统稳定的最大允许时滞上界值，是时滞系统稳定性结论保守性最普遍的衡量标准；MAPI (Minimum Allowable Performance Index) 定义为保证系统稳定的最小允许性能指标值，是时滞系统在零初始条件下所具有H∞扰动抑制水平的衡量标准。

例1首先考虑一类具有区间变时滞的线性系统，形如式(1)所示，其系统参数如下：

在该数值例子中，考虑两个性能指标，即H∞性能指标γ和MADB值hM。根据定理1，当时滞变化率μ=0和hm=0时，针对不同的H∞性能指标γ，表1仿真给出相应的MADB值；针对不同的MADB值，表2仿真给出相应的H∞性能指标γ。

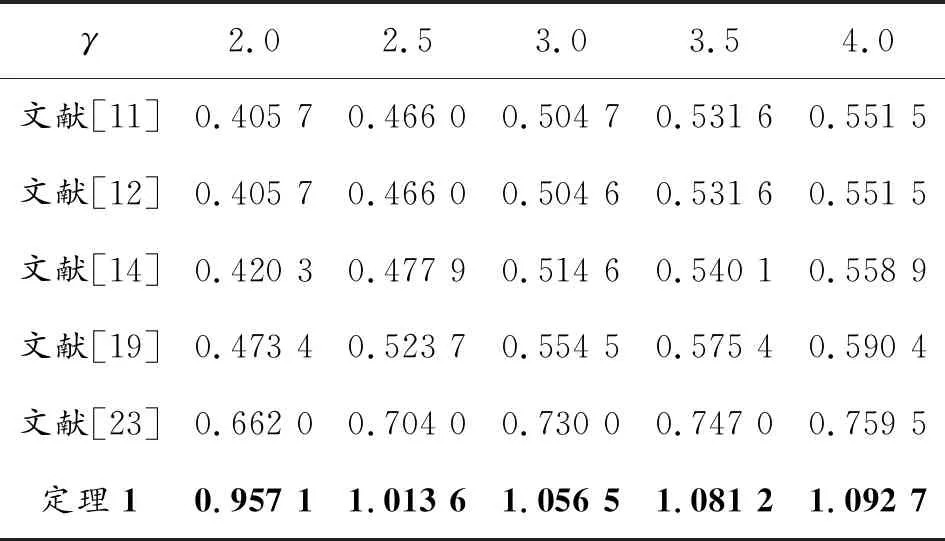
表1 针对不同的H∞性能指标γ，不同方法仿真给出的MADB值hM

通过表1和表2的比较，可以发现，对于指定的H∞性能指标γ，由定理1可以得出相应的MADB值。相比文献[11,12,14,19,23]，本文所提出的时滞相关有界实判据扩大了系统稳定的最大允许时滞上界范围，具有更低的保守性；另一方面，对于指定的MADB值hM，也可以求得相应的MAPI值。相比文献[11,12,14,23]，本文所提出的判据可以获得保证系统稳定的更小更佳H∞性能指标γ值。

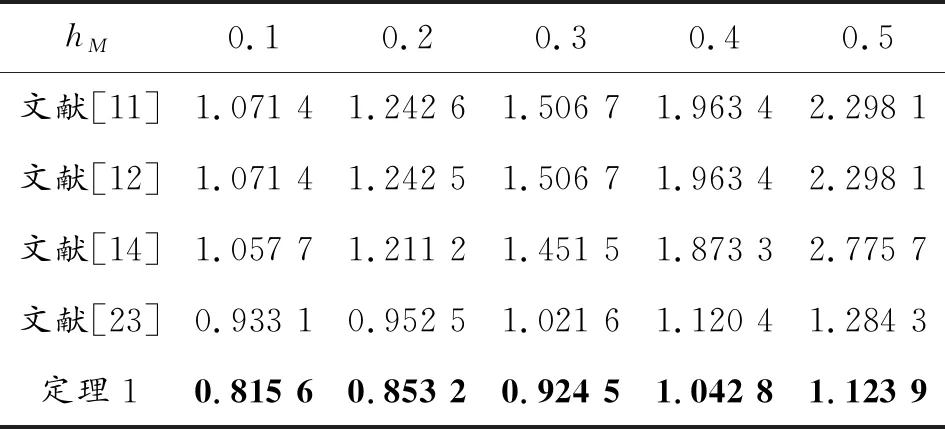
表2 针对不同的MADB值hM，不同方法仿真给出的MAPI值γ

例2下面以VTOL直升机为研究对象进行仿真。VTOL直升机的垂直起降控制过程是一种典型的含有时滞的动态控制系统[18]，其模型可描述为

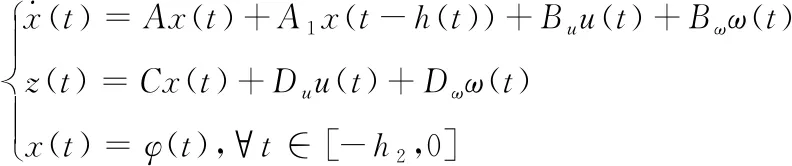
(35)

在不加外部控制(即u(t)=0)时，该控制系统的开环响应曲线如图1所示，显然系统是不稳定的。

为了说明本文所设计鲁棒非脆弱H∞控制器的优越性，下面以VTOL系统在不同控制器作用下的镇定性能来分析比较。

首先考虑控制器不存在外部干扰和增益摄动的情况。此时摄动参数Da和Ea均为零，取γ=0.9716，设时滞下界hm=0，hM=7，由定理2可得一般鲁棒控制器增益矩阵为

在K1作用下，系统状态响应曲线如图2所示。

其次考虑控制器存在外部干扰和增益摄动的情况。假设外部干扰为幅值0.1的正弦信号，控制器增益摄动参数Da和Ea均不为零，取γ=0.971 6，针对hM=7的定常时滞进行仿真，其中摄动参数取为：

扰动矩阵Fa∈R2×2，由定理2可得相应的鲁棒非脆弱控制器增益矩阵为：

在K2作用下，系统状态响应曲线如图3所示。以状态x1(t)为研究对象，图4比较给出了相同条件下，一般鲁棒控制器和非脆弱控制器的镇定效果。

由图2～图4可以看出：在非脆弱控制器K2作用下，系统状态能够获得更佳的性能指标，且容许控制器增益的摄动；而在一般控制器K1的作用下系统状态表现出明显的脆弱性，振荡较大，收敛较慢。

5 结论

本文采用时滞中点分割法和互凸组合技术并结合新的积分不等式处理方法研究了一类区间变时滞线性系统的时滞相关鲁棒非脆弱H∞控制问题，获得了LMI形式的时滞相关有界实判据和非脆弱H∞控制器。该控制器无需任何的参数调整和迭代处理，只需通过LMI的可行解即可得到控制器的参数表达式。最后将控制器应用于VTOL直升机的飞行过程，仿真过程说明所设计的控制器相比一般鲁棒控制器具有更好的镇定性能和非脆弱性。

附录

为了有效给出定理1的证明过程，首先令hΔ=χhm+(1-χ)hM,(0<χ<1)，则有hm

情形1:当hΔ≤h(t)≤hM时，设计如下L-K泛函：

V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))+

V4(x(t))+V5(x(t))

(6)

其中

计算L-K泛函V(x(t))沿系统(4)的导数，可得：

(7)

其中

xT(t-hΔ)Q2x(t-hΔ)-xT(t-hM)Q2x(t-hM)

(hM-hΔ)2xT(t)X3x(t)-

由引理1与引理2可得：

(8)

(9)

其中，ζ(t)同引理3中定义一致。

由引理3可得：

(10)

同样可以得到：

(11)

(12)

(13)

(14)

(15)

(16)

(17)

εΓ3+(1-ε)Γ4]ζ(t)

(18)

其中

因为0≤α,ε≤1，根据互凸组合技术，如下不等式成立：

α(Γ1+λ1I)+(1-α)(Γ2+λ1I)<0

(19)

ε(Γ3-λ2I)+(1-ε)(Γ4-λ2I)<0

(20)

即

αΓ1+(1-α)Γ2<-λ1I

(21)

εΓ3+(1-ε)Γ4<λ2I

(22)

由于λ1>λ2，合并式(21)、式(22)，可得

αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4<(λ2-λ1)I<0

(23)

对于给定的γ,考虑性能指标J(ω),则把z(t)Tz(t)-γ2ωT(t)ω(t)加到不等式(18)两边，可得：

(24)

其中，

如果

Ω+ΨTΨ+αΓ1+(1-α)Γ2+

εΓ3+(1-ε)Γ4<0

(25)

那么

(26)

-V(t)|t=∞+V(x(t))|t=0<0

(27)

即‖z(t)‖<γ‖ω‖2,从而闭环系统在零初始条件下具有给定的H∞扰动抑制水平γ。

情形2:当hm≤h(t)≤hΔ时，设计如下L-K泛函：

V0(x(t))=V01(x(t))+V02(x(t))+V03(x(t))+

V04(x(t))+V05(x(t))

(28)

其中

其中，

Pi(i=1,2,3,4,5)，Q1，Q2，U1，U2，Xj，Rj(j=1,2,3,4)，同式(6)中所定义的矩阵。利用同样的方法，可得

εΓ03+(1-ε)Γ04]ζ0(t)

(29)

其中

(30)

如果

Ω+ΨTΨ+αΓ01+(1-α)Γ02+

εΓ03+(1-ε)Γ04<0

(31)

那么

(32)

从而闭环系统在零初始条件下具有给定的H∞扰动抑制水平γ。

由于hM-hΔ=hΔ-hm，对式(18)或式(29)应用引理3，则其等价于式(5)。证毕。