矿井主通风机风量测试方法的数值模拟研究

王广知

（阳煤集团兴峪煤业有限责任公司， 山西 阳泉 045100）

引言

通风机故障导致其通风性能下降是瓦斯爆炸的主要原因之一，而风量则是评价通风机性能的主要参数[1]。综合国内外研究学者的已有研究成果，虚拟器技术、传感器技术及数值模拟分析手段已逐渐代替传统的风量测试方法，其中FLUENT软件被广泛用于确定巷道平均风速点与断面之间的关系。但实际生产过程中，关于风速的测定较为复杂，支架会对风量的测定产生一定的影响，需要在测定的过程中搭建支架固定风速传感器[2]。

1 风量测定方法及测风点位置确定

矿井主通风机的风量需要通过实际测量得到的风速及风压进行计算，风量的测试方法需要根据矿井实际情况进行选择，从而保证数据的准确性[3]。风速法是目前较为常用的测试方法，其计算方法为：

式中：S为巷道横截面积；v为巷道内平均风速。

矿井主通风机的风速测定是通过风速传感器测定。为减小数据的波动，应当将测风面设定在缓变流处，从而保证通过测风面的风流均匀分布。基于已有研究，本研究将测试点设置在风硐口，测试点的布置采用切贝切夫法，共设置24个测点，分布于a、b、c、d4条直线上，具体的测点布置如图1所示。

具体测量方法为，在选定的测风点搭建测量支架，并且根据所选择的测点位置安装风速传感器，利用风速传感器测得各点的风量后，根据公式（2）计算巷道风量。

图1 圆形巷道断面测点布置

式中：vi为测风断面上第i点的风速，m/s；S为巷道横截面积，m2；n 为测点数。

2 巷道内风流分布

巷道内风流主要以层流及紊流的形式存在，在矿井的实际生产过程中，层流的存在会对矿井中有毒有害气体的管理产生不利的影响，因此在实际生产中不允许矿井中出现层流的情况[4]。《煤矿安全生产规程》中指出，矿井最低风速为0.15m/s，根据现场测定及公式（3）的计算结果得到雷诺数Re＞2 320，即通风巷内的风流均为紊流状态。

式中：v为巷道平均风速；d为管径；μ为运动黏性系数。

矿井中大多数的风流状态都为紊流，仅在靠近巷道的边缘存在少量的层流，同时其厚度相对较低，流速低于空气流速，但紊流的流速相对较大，由巷道边缘至巷道中心逐渐增大，且巷道中线部位为紊流的核心，根据流体力学理论[5]，紊流也存在一定的规律性，其分布规律为：

式中：v'为切应力速度；k为试验常数，通常为0.4；y为流体层到巷道边缘距离；C为积分常数。

综上所述，圆形巷道中的流体的流动规律为，断面上流体速度为对数分布，轴心附近的流体速度变化显著，其紊流速度分布如图2所示。

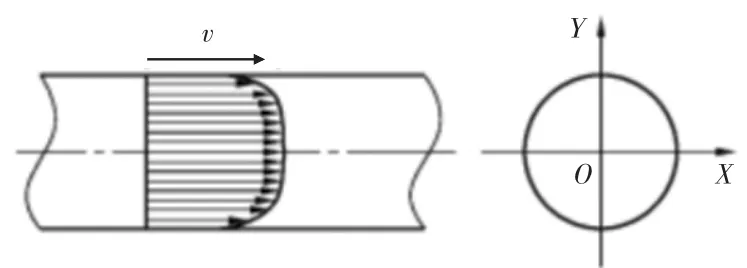
图2 圆形巷道紊流分布特征

3 FLUENT模拟方法及结果

在一般情况下，并没有研究风流传感器支架对巷道内风流分布的影响，但在实际测定过程中，由于流体的不可压缩性，风流在通过测风断面时会出现涡流区，从而导致流速的急剧改变，最终对风速造成影响。FLUENT主要用于研究复杂几何区域内的流体流动及热交换特性，可以在计算机上实现不同情况的模拟，不受时间及地点的限制，具有很强的灵活性，因此。基于以上优点，本文利用此软件对巷道内风流分布情况进行模拟，较为直观地观测风流分布情况，从而反应出支架对于风流的影响。

3.1 模型建立

试验模型为圆形风硐，通风机叶轮直径为2m。通常，风硐长度应当为风机叶轮直径的10～12倍，因此本试验选取风硐长度为24m。测风截面为距离通风机进风口1.5倍叶轮直径处，或选择距离通风机出风口约为5倍叶轮直径处，由此，本试验选取10m为测风截面。测点布置如上页图1所示，分别在A、B、C、D四点设置支架进行模拟计算，支架为0.03m×0.03m直杆。

3.2 巷道风速场模拟

1）网格划分。模型对于无支架的情况采用六面体网格进行划分，有支架的情况要用四面体进行划分，同时还包含六面体、楔形及锥形网格。模型中X、Y、Z轴分别代表断面的宽度、高度及风硐长度，选取风硐入口处中心作为原点。

2）条件假设及求解。本试验中仅考虑流场的分布，对于系统中存在的热交换及漏风等情况并不进行考虑。因此，系统中仅在风硐入口进风，且风流为不可压缩流体，巷道边缘的粗糙程度相同，试验中空气密度设为1.21 kg/m3。由于巷道内气体流动特性为湍流流动，因此选用的模型为k-ε模型，软件求解器为压力基求解器，速度为绝对速度，压力与速度的耦合关系采用SIMPLEC算法计算。

3）边界条件。软件设定的模型中风流的入口及出口分别为模型的边界入口及出口，巷道的边界作为固定边界。入口边界条件为velocity-inlet，风速为3m/s，靠近巷道边界的压力梯度为零，出口边界条件为outflow，壁面边界条件为无滑移。

3.3 结果及分析

1）无支架情况。对于无支架条件下的风流模拟，其巷道断面的风速等值线分布如图3所示，当断面中不存在支架时，风速为均匀分布，并且呈同心圆形式分布，没有出现明显的离层。截面外层的风速为零，中心处为最大值点，且流速散点图中的最高点基本位于同一直线上，与理论上的分布规律一致，如图4。

图3 速度（m/s）等值线分布图（无支架）

图4 速度分布曲线（无支架）

2）有支架情况。关于有支架情况下的断面风速等值线如图5所示。从图中可以看出，当风巷中存在支架后，断面的风流出现紊流，尤其是在支架附近紊流更为显著，与无支架情况下的风流分布存在较大的差异，其风速分布图如图6所示，从图中可以看出，在支架作用下，风速的变化比较显著，其中心位置风速变化最为显著，与已有的规律不同。

图5 速度（m/s）等值线分布图（有支架）

图6 速度分布曲线（有支架）

3）结果讨论。通过对有支架及无支架两种情况下风速分布进行模拟之后，分别得到了上页图1中24个测点的风速值，具体结果如表1所示。由表1中数据可知，在无支架的情况下，截面上的风速分布呈同心圆分布，相同半径上的风速值相同，越靠近轴心处风速越大；在支架存在的情况下，断面整体风速的分布紊乱，整体相对于无支架情况较低，从巷道边缘至轴心仍为逐渐增大的趋势，但存在某些点风速突变，最大误差可达到13.2%。无支架影响条件下的风速为2.96m/s，而在有支架影响的条件下平均风速为2.8m/s，相对误差为5.4%；无支架影响下的风量为37.18m3/s，支架影响下的风量为35.17m3/s，相对误差为5.4%，对应的误差线如图7所示，由图中结果可知，当巷道中存在支架后会对各点风速值存在影响，其中误差较大的点在截面中心附近，而巷道边缘的相对误差相对较低。

表1 测点风速表

图7 四条直径相对误差线

4 结论

本研究利用FLUENT软件对于圆形巷道中有无支架情况下的巷道中的风流分布情况进行模拟，模拟得到各点对应的风速值，结果表明：在巷道中安装支架会对巷道断面的风速测定产生影响，其最大相对误差可达13.2%。平均可以达到5.4%，对于风量的影响可以达到5.4%的相对误差。综合已有研究结果，可以对进一步改进矿井主通风机的风量测定方法及进行相关的误差补偿提供一定的理论指导。