不平整条件下过渡段车辆运行平稳性

沈宇鹏， 魏庆朝， 韩 浩， 左瑞芳

(1.北京交通大学土木建筑工程学院 北京，100044) (2.轨道工程北京市重点实验室 北京，100044) (3.北京市轨道交通线路安全与防灾工程技术研究中心 北京，100044)

1 问题的引出

由于道路自身因素及外部环境的影响，新建道路或是已经运营多年的既有道路的路面均存在不同程度的不平整。路面不平整会使行驶车辆产生附加振动，进而对路面产生附加荷载，造成路面破坏的加剧。在路桥过渡段上，由于桥台与路基之间存在差异沉降，这种破坏现象更为严重[1]。通常，路面不平整包括路面波浪形不平顺以及道路渠化交通引起的道路横向沉降不均等。实际路面波形不平顺模型如图1所示[2]。路面不平整降低了车辆的行驶速度和道路的通行能力，是道路交通安全的重要隐患，不仅会影响行车的安全性和舒适性，也会加剧车辆的轮胎磨损，增加运输成本。因此，如何降低路面的不平整性，特别是过渡段路面的不平整性是路桥过渡段研究的关键。对此，许多学者开展了广泛研究。

图1 路面波形曲线图Fig.1 The pavement wave curve

梁波等[3]通过建立车辆-道路垂向耦合动力模型，得到了车辆-道路系统的动力平衡方程，把路面不平整设定为振动激励函数，对动力平衡方程进行求解，通过编程并结合算例，分析了车辆运行速度、路面不平整度的矢高和波长与车辆动荷载及车身加速度的关系。王康[4]将搭板计算工况分成均匀沉降和局部脱空两种情况，计算结果表明，搭板截面内力较大，配筋量较多，适宜长度为5～8 m。李智峰等[5]对设置搭板的路桥过渡段路面进行简化，采用D-P弹塑性本构模型描述路基土(包括地基)材料的本构关系，通过改变搭板厚度和长度分析了路桥过渡段差异沉降对搭板性能的影响。研究发现，在一定沉降差异的影响下，增加搭板长度仅利于搭板的受力，搭板厚度的增加对搭板的受力和变形均有利。搭板由于其刚度比较大，在过渡段中能有效改善路面的不平整[6]，但是在实际工程中对于搭板改善过渡段路面不平整的具体效果仍没有进行量化。当左右轮车辙沉降不均时，搭板对车辆运行平稳性的改善效果还不清楚。

笔者通过ABAQUS有限元软件建立了路桥过渡段及七自由度整车耦合三维模型，并用现场测试数据验证模型的正确性。研究了搭板对改善不同路面等级不平顺效果以及车辙的影响，为实际工程中搭板的运用提供一定的参考。

2 路面不平整的原因及表现形式

产生路面不平整的主要原因[7]包括：a.路基不均匀沉降；b.桥头或涵洞与道路接头处及伸缩缝引起的桥头跳车；c.路基不平整对路面平整度的影响；d.路面摊铺机械及工艺对平整度的影响。

由于路面材料的不同，水泥路面和沥青路面常见的破坏类型也会不同。水泥路面常见的破坏类型[8]如表1所示。

表1 水泥路面常见破坏类型

沥青路面由于受行车荷载的反复作用以及在自然因素的不断影响下会逐渐出现破坏，造成路用性能逐步恶化，常见的破坏类型[9]主要有车辙、裂缝、剥落、波浪以及泛油等。车辙主要是由于沥青路面在行车荷载的作用下，被压密、挤压、路面轮迹带下沉、两侧面鼓起进而形成波峰和波谷状，波峰和波谷的高差即为车辙深度[10]。道路渠化交通主要是由于沥青路面受力不均而产生车辙，在长期累积荷载作用下形成的道路沿横向沉降不均[11]。

3 车辆运行平稳性评价指标的选取

对于车辆行驶舒适性的评价，文献[12]提出了吸收功率(absorbed power，简称AP)法。国际标准化组织从20世纪60年代开始制定“人体承受全身振动的评价指标”，并在1974年颁布了IS02631-1974(E)国际标准，经过几次补充和修订，确定为国际标准IS02631/1-1985[13]。目前，IS02631推荐的1/3倍频带分别评价方法、总加权值评价方法及其评价指标仍被普遍采用[14-15]。

动荷载系数是评价车辆振动剧烈程度的一个重要指标。在公路标准载荷下，一般A级路面动载系数为1.12～1.19，B级路面动载系数为1.23～1.38，C级路面动载系数为1.48～1.76，D级路面动载系数为2.00～2.52[16]。动荷载系数越大，说明车辆在道路上运动时的振动越剧烈，行车越危险。

笔者选取车体垂向加速度、车轮动荷载系数、前后轮垂向位移差作为车辆运行平稳性的评价指标。车体垂向加速度越大，人体越不舒适；动荷载系数越大，车辆振动越剧烈；前后轮垂向位移差越大，安全性和舒适性越差。加权加速度均方根与人体行驶舒适性的关系详见文献[13]。

4 模型建立及验证

利用ABAQUS有限元分析软件[17]建立了路桥过渡段及七自由度整车耦合三维模型，如图2所示。分析了搭板对路面波浪形不平顺以及道路渠化交通的改善作用,侧视图如图3所示。行车方向为由路基侧驶入桥梁。

图2 七自由度整车模型Fig.2 Vehicle model in seven DOFs

图3 七自由度整车模型侧视图Fig.3 Vehicle model in seven DOFs′ side view

模型中的参数[18-23]分别如下：mb为汽车簧载质量；mwi(i= E，F，G，H)为非悬挂质量；Ksi(i= E，F，G，H)为悬挂系统刚度；K1i(i= E，F，G，H)为轮胎刚度；Csi(i= E，F，G，H)为悬挂系统阻尼；Xwi(i= E，F，G，H)为非悬挂质量的垂直位移；Xbi(i= E，F，G，H)为悬挂质量的垂直位移；Xb为悬挂质量质心处的垂直位移；XBi(i= E，F，G，H)车轮处路面的随机激励即路面之间的不平度；E，F为车体前轮对；G,H为车体后轮对；Lf为各轴至车体质心的垂直距离；θ，φ为簧上系统质心绕轴的转角。

以解放CA1253P7K1L11T16×4型汽车为例，构建的七自由度整车模型参数[18]如表2所示。

表2 车辆模型参数

由图3整车模型侧视图可以看出，车体簧载质量在车辆质心处通过MPC梁传到车辆悬挂系统，即参考点处，然后通过悬挂系统传到车轴，再通过车轴传到轮胎，最后通过轮胎与路面之间弹性接触传到路面。

路面纵向波形不平整是将不平整波形数据用强制位移施加到路面网格节点上，路面波形被简化为沿道路纵向凹凸不平的折线位移。因此，路面网格需尽可能采用小尺寸，波形图如图4所示。

图4 A级路面波形图Fig.4 A-grade road waveform

对左右车轮所处路面沉降不均进行简化时，主要是将左右车轮所处路面分别施加一个纵向的沉降曲线，如图5所示。

图5 路面不均匀沉降示意图Fig.5 The road uneven settlement schematic diagram

为了验证所建立模型的正确性，笔者采用七自由度重载车辆模型参数[16]，将沥青路面结构简化为4层：沥青面层、半刚性材料基层、半刚性材料底基层及土基层。各层均由均质、各向同性的线弹性材料组成，各结构层参数如表3所示。在面层下部设置混凝土搭板，搭板厚度为30 cm，材料参数为C30混凝土。

表3沥青路面结构层材料参数

Tab.3Thephysicalandmechanicalparametersofasphaltpavement

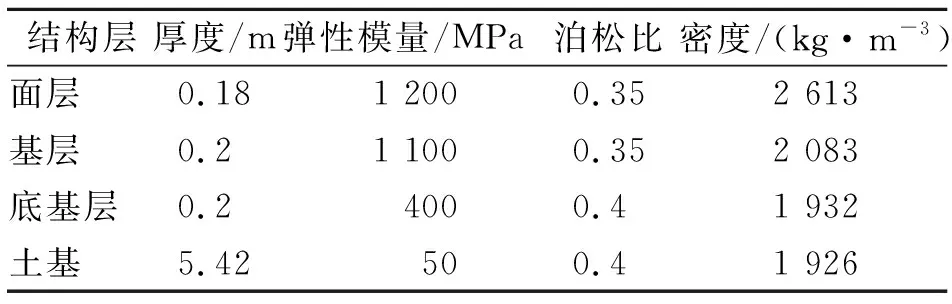
结构层厚度/m弹性模量/MPa泊松比密度/(kg·m-3)面层0.181 2000.352 613基层0.21 1000.352 083底基层0.24000.41 932土基5.42500.41 926

考虑路面结构在水平和竖直方向的无限伸展，边界条件为底部完全固定，x,z方向固定，深度y方向无约束。对于桥梁结构采取3 m×13 m梁式箱梁，箱梁下部的桥墩结构用竖向弹簧代替，各结构层材料均匀，层与层之间连续。轮胎采用面积等效的办法[24]简化为长方形，前后轮胎的尺寸分别为Sf=Bf×Lf=0.064 m2，Sr=Br×Lr=0.139 5 m2(其中：S为车轮面积；B为车轮宽度；L为车轮长度；下标f，r分别表示前轮和后轮)。

在道路的同一点处，当车辆分别以5 km/h和70 km/h通过上述路面时，将计算得到的道路纵向应变的数据与文献[25]中的实测数据进行比较，验证模型的正确性，如图6所示。可以看出，模型和实测数据的趋势非常吻合，都是前后轮分别经过该路段时产生两个极值，说明模型采用的假设条件和计算结果符合实际情况。

图6 路基底部纵向应变对比Fig.6 Comparison chart between field measure and simulation of vertical strain on the bottom of the subgrade

5 结果分析

5.1 路面波浪形不平顺的动力特性

根据我国《机械振动道路路面谱测量数据报告》(GB/T 7031-2005/ISO 8608:1995)[26]中的规定，基于路面不平整程度将道路分为A～H共8个等级，并给出了各自的功率谱密度，如图7所示。

图7 道路分级与位移功率谱密度Fig.7 The relation curve between road classification and displacement power spectrum density

图8 B级路面波形图Fig.8 B-grade road waveform

图9 C级路面波形图Fig.9 C-grade road waveform

笔者采用傅里叶逆变换方式，将A，B，C级路面的位移功率谱密度转化为路面不平度的空间分布，如图4，8，9所示。该车辆对应的不平顺有效波长范围为1.11～33.3 m，不平顺有效空间频率范围为0.03～0.9 m-1。3种路面不平度样本的统计特征在0.03～0.9 m-1的空间频率范围内，与规范[19]中对应等级的功率谱密度曲线接近，可以代表该等级路面进行动力学分析。

分别取A，B，C三种路面建立路面三维不平整度模型，计算不同等级路面对车辆运行平稳性的影响。以B级路面为例，分析在过渡段有且无搭板的情况下，路面随机不平顺对车辆运行平稳性的影响。

图10为车体的垂向加速度时程曲线。当车辆刚进入过渡段时，设置搭板对减小车体振动效果不明显。当经过0.25 s车辆完全驶入过渡段后，在有设置搭板路段，车体垂向加速度变化的幅值越来越小，最大值仅为1.40 m/s2，处于人体不舒适标准[12]。对于无搭板的路段，车辆在进入过渡段过程中， 车体加速度变化幅度大， 最大达1.62 m/s2，处

图10 车体垂向加速度时程曲线图Fig.10 Car′s vertical acceleration-time curve

于人体非常不舒适标准[12]。

图11为车辆的前后轮垂向位移差时程曲线。可以看出，车辆的前后轮竖向位移差在有、无搭板的情况下对比较吻合。当经过0.25 s车辆完全进入过渡段后，在有搭板时，前后轮垂向位移差最大值为32.9 mm，然后保持在10 mm左右，即车体的倾斜度为0.65%；在无搭板时，前后轮垂向位移差最大值为38.4 mm，即车体的倾斜度达0.76%，且以一个较大的幅度上下波动。

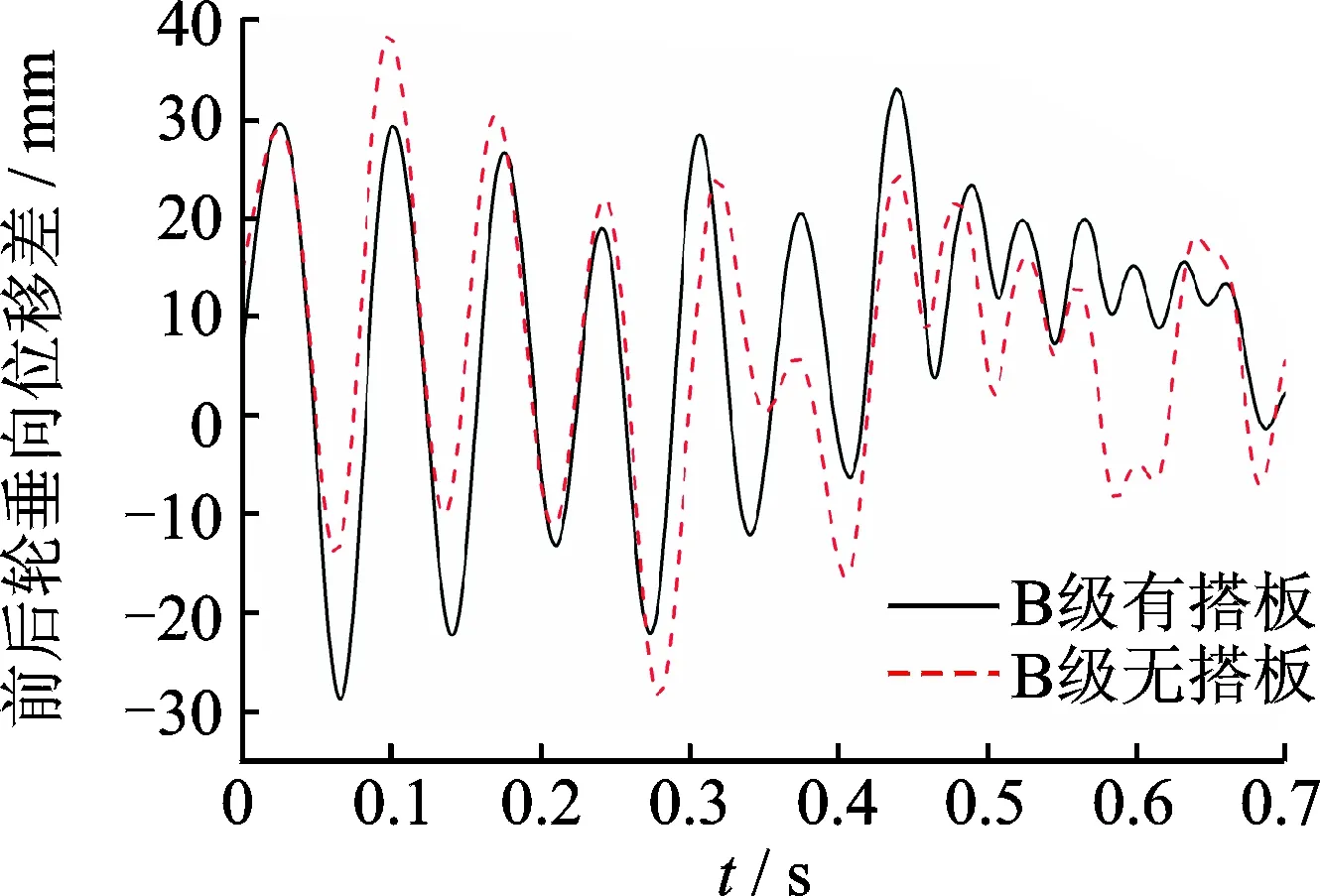
图11 前后轮垂向位移差时程曲线图Fig.11 The front-rear wheel′s vertical displacement difference-time curve

图12，13分别为前、后轮动荷载系数时程曲线。有、无搭板时，后轮最大动荷载系数基本保持在2.10左右；无搭板时前轮最大动荷载系数为4.51，设置搭板可以将其降低到4.43。

图12 前轮动荷载系数时程曲线Fig.12 The front-wheel′s DLC-time curve

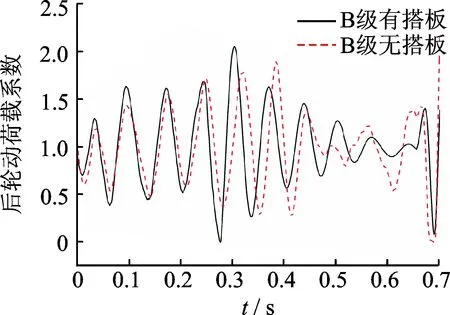
图13 后轮动荷载系数时程曲线Fig.13 The rear-wheel′s DLC-time curve

同样的方法得到A级和C级路面工况下车辆的评价指标值。对其进行整理，得到不同路面下车辆运行指标值，如表4所示。路面等级与车体加速度曲线如图14所示。

图14 路面等级与车体加速度关系曲线Fig.14 The relationship between car′s vertical acceleration and road grade

图15为路面等级与前后轮竖向位移之差关系曲线。可以看出，路面等级越低，前后轮垂向位移差越大；路面等级越低，搭板对前后轮垂向位移差的减小越明显。

图16为路面等级与前后车轮动荷载系数关系曲线。可以看出，随着路面等级的降低，前后车轮的最大动荷载系数都随之增大；有无搭板对后轮动荷载系数影响不大；设置搭板可明显降低前轮动荷载系数。

表4 不同等级下车辆运行平稳性评价指标值

图15 路面等级与前后轮垂向位移差关系曲线Fig.15 The relationship between the front-rear wheel′s vertical displacement difference and road grade

图16 路面等级与前后轮垂向位移差关系曲线Fig.16 The relationship between the wheels′ DLC and road grade

5.2 左右车轮所处路面沉降不均的动力特性

针对左右车轮所处路面沉降不均的现象，主要考虑两种情况：a. 右侧车轮处在没有搭板的道路沉降中、左侧车轮处在有搭板且搭板厚度为30 cm的道路沉降中，如图5所示；b. 右侧车轮处在有搭板且搭板厚度为45 cm的道路沉降中、左侧车轮处在有搭板且搭板厚度为30 cm的道路沉降中，如图17所示。

图17 路面不均匀沉降示意图Fig.17 The road uneven settlement schematic diagram

车辆进入过渡段时，车体垂向加速度时程曲线如图18所示。可以看出，当左侧车轮所处路面搭板厚度为30 cm时，随着右侧车轮所处路面搭板厚度的增加，车体的垂向加速度逐渐减小；右侧车轮处在无搭板的路面时，车体的最大垂向加速度为1.92 m/s2；右侧车轮处在搭板厚度为30 cm时，车体最大垂向加速度为1.13 m/s2；右侧车轮处在搭板厚度为45 cm时，车体最大垂向加速度为1.03 m/s2。相对于右侧车轮处在没有搭板下路面，处在搭板厚度为30 cm路面时，车体垂向最大加速度变化显著，降低了41.1%。当搭板厚度由30 cm增加到45 cm时，搭板对车体加速度的改善效果不明显。

图18 车体垂向加速度时程曲线Fig.18 Car body′s vertical acceleration-time curve

车辆进入过渡段时，车体前、后左右轮垂向位移差时程曲线分别如图19，20所示。当左侧车轮处在板厚都为30 cm路面、右侧车轮处在无搭板路面时，前、后左右轮最大垂向位移差均为-37.5 mm，即车体的倾斜角度为0.74%。右侧车轮处在板厚为30 cm路面时，前、后左右轮垂向位移差为0，车辆行驶非常平稳。右侧车轮处在板厚为45 cm路面时，前、后左右轮最大垂向位移差为9.8 mm，即车体倾斜角度仅为0.19%。可见，从车轮垂向位移差角度考虑，搭板对改善左右车轮所处路面沉降不均的效果比较明显。

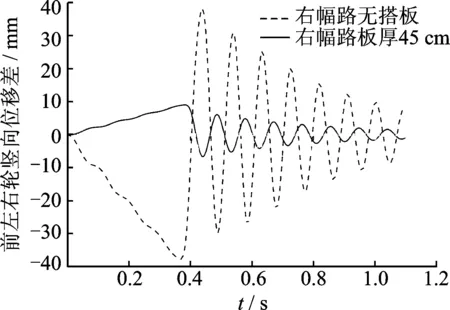
图19 前左右轮垂向位移差时程曲线Fig.19 The front-left wheel and front-right wheel′s vertical displacement difference-time curve

图20 后左右轮垂向位移差时程曲线Fig.20 The rear-left wheel and rear-right wheel′s vertical displacement difference-time curve

6 结 论

1) 车体加速度、车轮动荷载系数及前后轮垂向位移差能够直观、精确地反应车辆运行变化规律，可以作为评价车辆运行平稳性评价指标。

2) 无搭板时，随着路面等级的降低，车辆振动的越来越剧烈，此时车体最大垂向加速度由0.96 m/s2增大到3.78 m/s2。当路面为C级时，人体已经感到特别不舒适，前后轮最大垂向位移差由20.5 mm增大至114.8 mm。

3) 有搭板时，随着路面等级的降低，车体最大垂向加速度由0.87 m/s2增大到2.93 m/s2。当路面为C级时，人体依旧感到特别不舒适，但较无搭板情况有所缓解。前后轮最大垂向位移差由18.7 mm增大到34.2 mm，相对于无搭板时，搭板对等级更低的路面的改善效果更加明显。

4) 搭板的设置对改善后轮动荷载系数作用不大，但是可以有效地降低前轮动荷载系数，并将其提高到更高一级路面水平。

5) 在考虑搭板对左右车轮所处路面沉降不均的改善效果时，当由无搭板到板厚为30 cm的过程中，车体最大垂向加速度由1.92 m/s2降到1.13 m/s2。随着搭板厚度由30 cm增大到45 cm的过程中，车体最大垂向加速度由1.13 m/s2降到1.03 m/s2，此时最大加速度仍处在人体不舒适的范围之内。可见，当道路出现左右车轮所处路面沉降不均时，搭板对车体垂向加速度的改善效果不显著，需采取其他工程补救措施。