基于VMD-HHT边际谱的水工结构损伤诊断
张建伟, 侯 鸽, 华薇薇, 赵 瑜, 马晓君, 黄锦林
(1.华北水利水电大学水利学院 郑州,450046) (2.水资源高效利用与保障工程河南省协同创新中心 郑州,450046) (3.河南省水工结构安全工程技术研究中心 郑州,450046) (4.广东省水利水电科学研究院 广州,510635)
引 言
水工结构在我国水利事业的长远发展中起到重要作用,但由于其工作条件复杂,在各种荷载以及环境侵蚀等因素的综合作用下易发生损伤,严重时导致其整体破坏,影响人们的生命财产安全。因此,必须对水工结构的损伤加以重视,确保其安全运行[1]。
损伤特征信息提取是进行水工结构损伤诊断的核心与前提[2]。在实际运行过程中,由于受到环境激励的高频白噪声和低频水流噪声的干扰,水工结构的振动信号通常表现为低信噪比的非平稳随机信号。如何从获取的振动信号中提取损伤特征信息,在水工结构损伤诊断中显得尤为重要。传统的非平稳振动信号分析方法如Fourier变换[3]、Winger分布[4]和小波变换[5]等在损伤诊断方面取得了一定的成果,但这些方法在分析信号的过程中不具有自适应分解的特性,限制了在损伤诊断领域的发展。Hilbert-Huang变换[6]是一种自适应的信号分析方法,该方法无需提前设定基函数,克服了小波变换等传统信号处理方法依赖主观经验的缺点,具有良好的自适应分解特性。基于HHT的优点,国内学者将其应用于不同领域的结构故障诊断。耶晓东[7]对轴承故障诊断进行了研究。陈希等[8]对转子振动故障诊断进行了研究。由于缺乏完备的数学理论,基于EMD的HHT方法在实际应用过程中存在端点效应、模态混叠等问题。因此,许多学者提出一些改进方法弥补HHT的不足。张鑫等[9]提出了聚合经验模态分解(ensemble empirical mode decomposition,简称EEMD)和HHT相结合的滚动轴承故障诊断方法。李慧梅等[10]将局部均值分解(local mean decomposition,简称LMD)和Hilbert边际谱相结合进行滚动轴承的故障诊断。上述改进方法虽取得了较好的结果,但仍有很大的局限性。EEMD算法在一定程度上解决了模态混叠问题,但其计算效率低[11]。LMD在解调过程中易造成信号突变。针对上述问题,文献[12]提出一种适用于非平稳信号分析的变分模态分解方法,该方法通过循环迭代确定各IMF分量的带宽和频率中心,将信号分解为多个IMF分量。由于自适应地选择带宽,VMD能够有效抑制模态混叠[13]。与EMD,EEMD和LMD相比,VMD具有收敛快、计算效率高和鲁棒性高等特点[14]。
针对环境激励下水工结构损伤特征提取和运行状态识别困难的问题,笔者提出一种VMD和HHT边际谱相结合的水工结构损伤诊断方法。该方法依据VMD算法基本原理构造VMD边际谱,定义损伤灵敏指数来提取结构的损伤特征,采用马氏距离对水工结构进行损伤诊断,判断其运行状态,从而为水工结构的安全运行和健康状态评价提供参考。
1 基本原理
1.1 数据级融合方法-方差贡献率
鉴于水工结构运行条件比较复杂,测点位置的布置对其振动信号的影响较大,单测点测试数据反映的结构运行特征信息有限,因此需要采用有效的数据融合方法提取结构完整的运行特征信息。传统的数据融合方法有加权平均法、HIS变换、数据一致性融合方法、互相关融合方法等,其目的是将结构的局部数据信息通过一定的组合方式进行综合,得到一组真实反应结构整体振动特性的新数据,但其不足之处在于对信号相似度要求较高,易导致有效特征信息的丢失。李火坤等[15]提出了方差贡献率数据融合算法,实现了多测点振动信号的动态融合并通过仿真试验验证该方法的有效性。该方法已成功应用于蜀河水电站和二滩拱坝等水利工程,取得了较好的效果。
方差贡献率数据融合算法通过计算信号的方差贡献率,使振动信号的融合系数在不同时刻随方差贡献率呈现动态变化过程,从而实现融合系数的动态分配。该方法在使用同种传感器进行数据采集的基础上,能够将大量原始信息进行融合,自动将信号中的重要信息筛选出来,能更贴切地反映结构振动特性。文献[15]对其理论进行了详细研究。
1.2 VMD-HHT分析方法
1.2.1 变分模态分解
VMD算法的实质是通过构造变分问题,寻求变分最优解确定每个IMF分量的带宽和中心频率,使分解得到的各IMF的带宽之和最小,从而实现信号的有效分离[16]。
为确定IMF分量带宽,具体步骤如下:a.利用Hilbert变换对各IMF进行处理,获取其单边频谱;b.加入预估中心频率e-jωkt,将每个IMF分量的频谱调制到基带上;c.通过计算信号梯度的平方L2范数确定各IMF分量的带宽。假设原始信号经过VMD分解后得到K个IMF,变分约束模型表示为
(1)
其中:μk=μ1,μ2,,μk为分解得到的各IMF分量;ωk=ω1,ω2,,ωk为各IMF的中心频率;f为原始信号。
为求解上述变分约束模型,使计算结果更加收敛,在该模型中引入二次惩罚项α和Lagrange因子λ[11]。VMD算法的实现过程如下:
2) 令n=n+1,执行整个算法的循环过程;
3) 令k=0,k=k+1,根据式(2)和式(3)更新μk和ωk
4) 更新λ
(4)
其中:τ为噪声容限参数。
5) 重复步骤2~4,对于给定的判别精度e>0,直到满足式(5)的约束条件停止迭代
(5)
1.2.2 Hilbert谱与Hilbert边际谱
利用Hilbert变换对VMD分解得到的每个IMF分量进行处理,则原始信号可表示为
(6)
其中:Re表示实部;ωit和ait分别为信号的瞬时频率和瞬时振幅。
由于x(t)是关于时间t和瞬时频率ωit的函数,故表示为
(7)
Hω,t即为Hilbert谱,对其积分,得到边际谱hω为
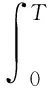
(8)
hω有效凸显了振动信号的幅值随瞬时频率的变化。常用的功率谱只能反映某一频率存在的可能性大小,而边际谱幅值能够精确反映某一频率是否真实存在,表征某特定频率在不同时刻对应的幅值(或能量)之和,某一频率对应的幅值发生变化,其对应的能量也随之改变。此外,边际谱与常用的功率谱相比,准确性和分辨率显著提高,能够有效抑制能量泄漏[17]。鉴于边际谱的上述优点,将其与VMD结合进行损伤诊断。
1.2.3 损伤灵敏指数Q
模态能有效反映结构的振动特性,表征结构在各种振源激励下的振动响应。工作模态参数是结构运行状况的动态外在表现,当结构发生损伤、运行状态改变时,其工作模态参数也会改变。根据结构工作模态参数的变化可以判断结构的不同运行状态,实现结构的损伤识别。由于应变模态对结构的损伤较敏感[18],笔者根据应变模态的变化识别水工结构的不同运行状态,进而确定结构的损伤。由于结构边际谱的峰值来源于应变模态,因此依据结构的边际谱图可得到应变模态的幅值及频率。考虑到相同损伤程度,不同水工结构的应变模态不同,其绝对值的大小并不能有效地反映应变模态对结构损伤的灵敏程度。为避免由于个体差异对计算结果造成的影响,定义损伤灵敏指数Q为
(9)
其中:fM为边际谱的峰值所对应的频率;Pf为频率为f的信号的幅值。
以羊腿股二头肌为取样点,每组分别从原料腿(0 d)、腌制结束(3 d)、风干前期(8 d)、风干中期(15 d)、风干后期(23 d)、成熟期(30 d)等六个工艺点取样,置于-20 ℃冷冻保藏,以备各指标的测定。
1.3 马氏距离
马氏距离是由印度统计学家Mahalanobis提出的判断样本归属的方法。其计算建立在总体样本的基础上,不受量纲的影响,具有算法简单和计算速度快等特点,在模式识别中具有明显优势[19]。


(10)
比较d1,d2,,dk的大小,选取最小马氏距离对应的损伤状态作为被诊断信号的损伤类型。
2 VMD-HHT边际谱的水工结构损伤诊断
基于VMD-HHT边际谱的水工结构损伤诊断流程如图1所示。基于VMD-HHT边际谱的水工结构损伤诊断步骤如下。
1) 采用笔者提出的小波阈值-EMD联合降噪技术[20]对原始信号降噪,滤除其中的低频水流噪声和高频白噪声,减小环境激励对结构损伤特征信息的干扰,提高信号的信噪比。
2) 运用方差贡献率信息融合技术计算降噪后各个测点信号的方差贡献率,以方差贡献率为依据,根据信息的相对重要性分配融合系数,实现不同测点信号信息的动态融合,提取结构的完整工作特征信息。
3) 利用VMD算法将包含结构完整工作特征信息的动态融合信号分解为若干个IMF分量之和,再利用Hilbert变换对各IMF进行处理,求其边际谱hω。

6) 比较d1,d2,,dk的大小,选取最小判别距离所对应的状态作为被诊断信号的损伤类型,从而判断水工结构的运行状态。

图1 基于VMD-HHT边际谱的水工结构损伤诊断流程Fig.1 Flowchart of damage diagnosis based on VMD and HHT marginal spectrum
3 模型试验
3.1 试验概况
为验证本研究方法的合理性,进行泄流激励下悬臂梁损伤模型试验。试验时,用水流模拟悬臂梁结构运行过程中所受的环境激励,采用智能数据采集和信号分析系统对泄流激励下悬臂梁结构的动应变响应进行测试。悬臂梁模型材料的弹性模量E=155 MPa,ρ=2 321 kg/m3,结构的长×宽×高尺寸为6cm×4cm×40cm,将其底部用AB胶固结在有一定重量和厚度的钢板上,钢板与水槽底部用橡皮泥固定,以防止水流激励把模型掀翻。在悬臂梁的背水面布置5个应变传感器,传感器采用等间距布置方式,测点编号自上而下依次为1~5。采用同样的布置方式在悬臂梁的一个侧面布置5个传感器,其测点编号自上而下依次为6~10。为了降低试验时温度等因素对应变片测试结果造成的影响,在同一试验环境中布置温度补偿片,测点及温度补偿片布置如图2所示。悬臂梁流激振动试验如图3所示。

图2 测点及温度补偿片布置图Fig.2 Measured points layout plan and temperature compensation plan

图3 悬臂梁流激振动试验Fig.3 Cantilever beam vibration test
3.2 泄流激励下的结构损伤诊断
泄流激励下结构测试采样频率fs=300Hz,采样点为4 096。试验设置4种工况:a.3测点0损伤(无损伤);b.3测点5mm损伤;c.3测点10mm损伤;d. 3测点15mm损伤。各工况的损伤均为贯通裂纹。限于篇幅,仅给出3测点在4种工况下的应变时程线,如图4所示。
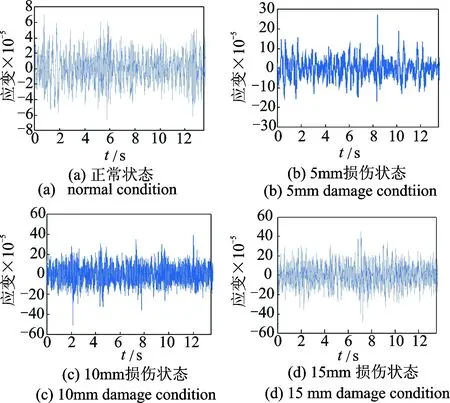
图4 不同工况下3测点原始信号的应变时程Fig.4 Time history curves of measured point 3 under different working conditions
由于受到环境激励作用下低频水流噪声和高频白噪声的影响,结构振动的特征信息被噪声淹没,这会降低结构损伤诊断的精度。因此,采用小波阈值-EMD联合降噪技术对不同测点各工况下的原始信号降噪。限于篇幅,在此仅给出10mm损伤,即工况3中测点3原始信号滤波前后的时程对比及局部放大图,结果如图5所示。
鉴于水工结构运行条件比较复杂,测点位置的布置对振动信号的影响较大,单测点测试数据反映的结构运行特征信息有限,因此运用方差贡献率信息融合技术实现多测点(1~5测点)信号振动信息的动态融合,提取结构的完整工作特征信息。限于篇幅,在此仅给出0损伤和5mm损伤工况下1~5测点降噪后信号的动态融合信号,结果如图6所示。
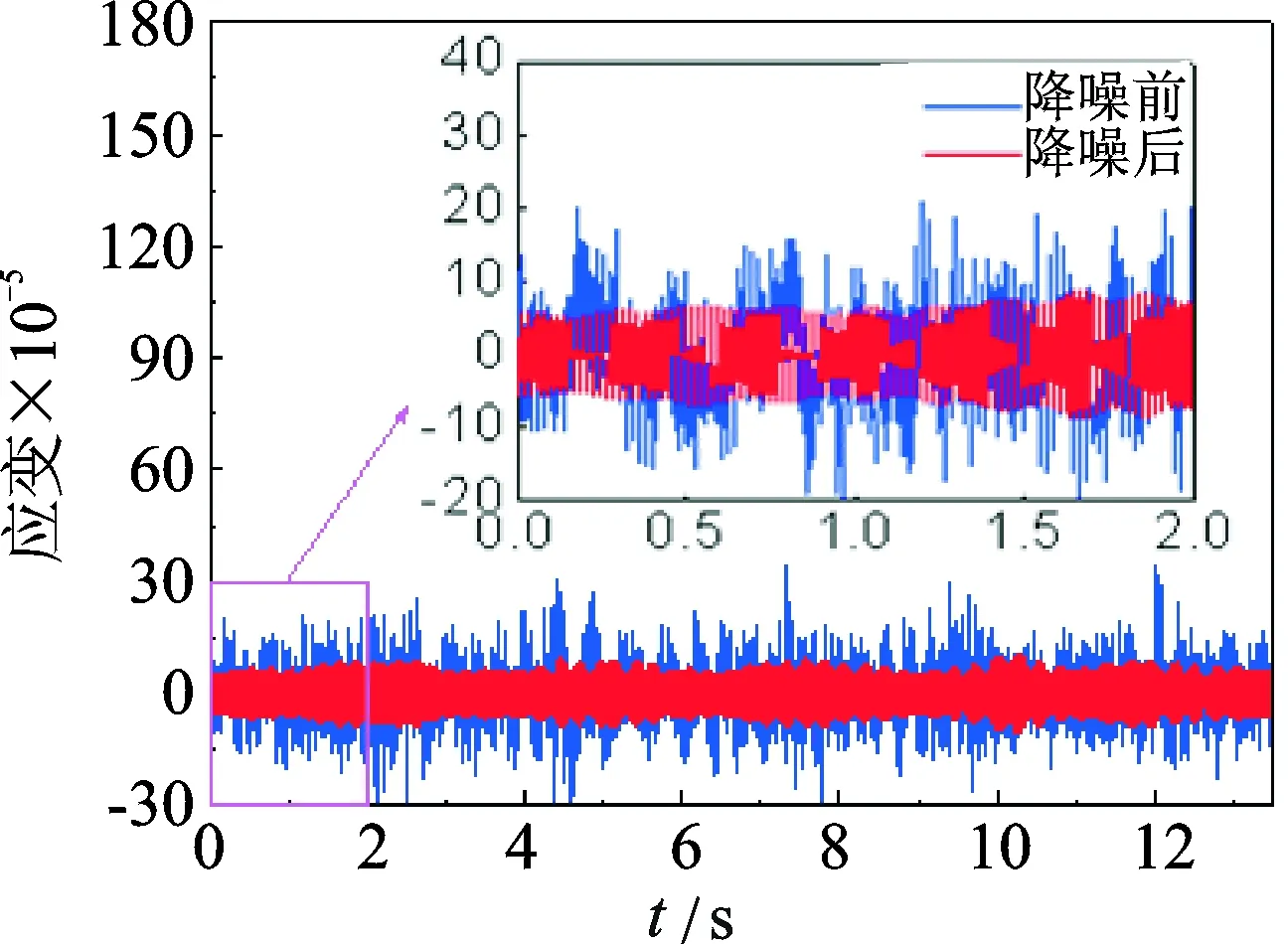
图5 10mm损伤工况下3测点降噪前后时程对比及局部放大图Fig.5 Time history comparison and local enlarged drawing of signal at point 3 under condition 3
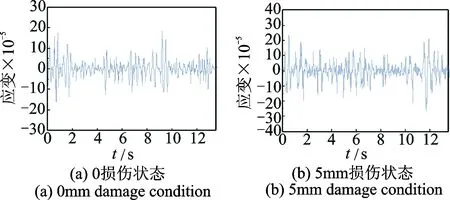
图6 不同工况下融合信号的应变时程图Fig.6 Time history curves of fused signal under different working conditions
利用VMD算法将包含结构完整工作特征信息的动态融合信号分解为一系列从高频到低频的IMF分量,然后利用Hilbert变换对各IMF分量进行处理,求出其相应的边际谱hω。以15 mm损伤工况下的融合信号为例,其Hilbert边际谱如图7所示。

图7 15mm损伤工况下融合信号的Hilbert边际谱Fig.7 Hilbert marginal spectrum of the fused signal under 15mm damage condition
每种工况随机选取20组样本信号,对其进行降噪、信息融合及边际谱处理。根据式(9)确定不同工况下各样本信号的损伤特征向量,即损伤灵敏指数Q,如图8所示。
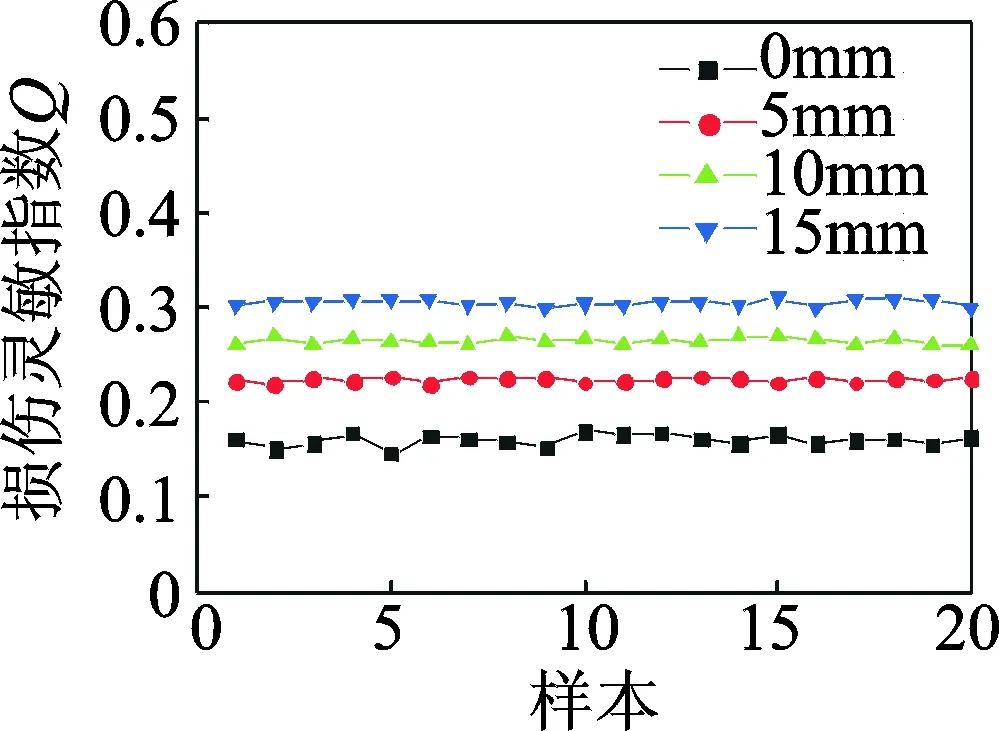
图8 损伤灵敏指数对比图Fig.8 Comparison of damage sensitive index

表1标准特征向量及其方差
Tab.1Standardfeaturevectoranditsvariance
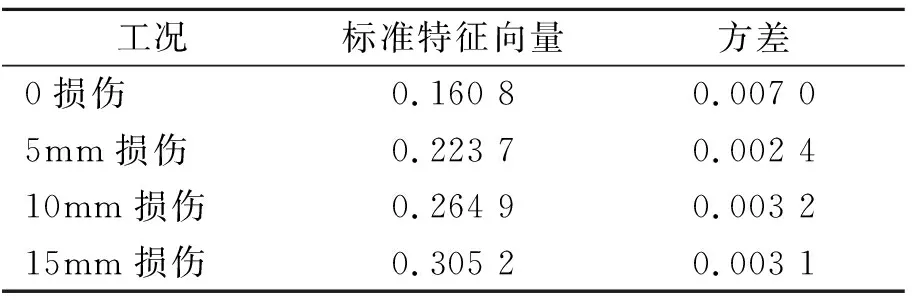
工况标准特征向量方差0损伤0.160 80.007 05mm损伤0.223 70.002 410mm损伤0.264 90.003 215mm损伤0.305 20.003 1

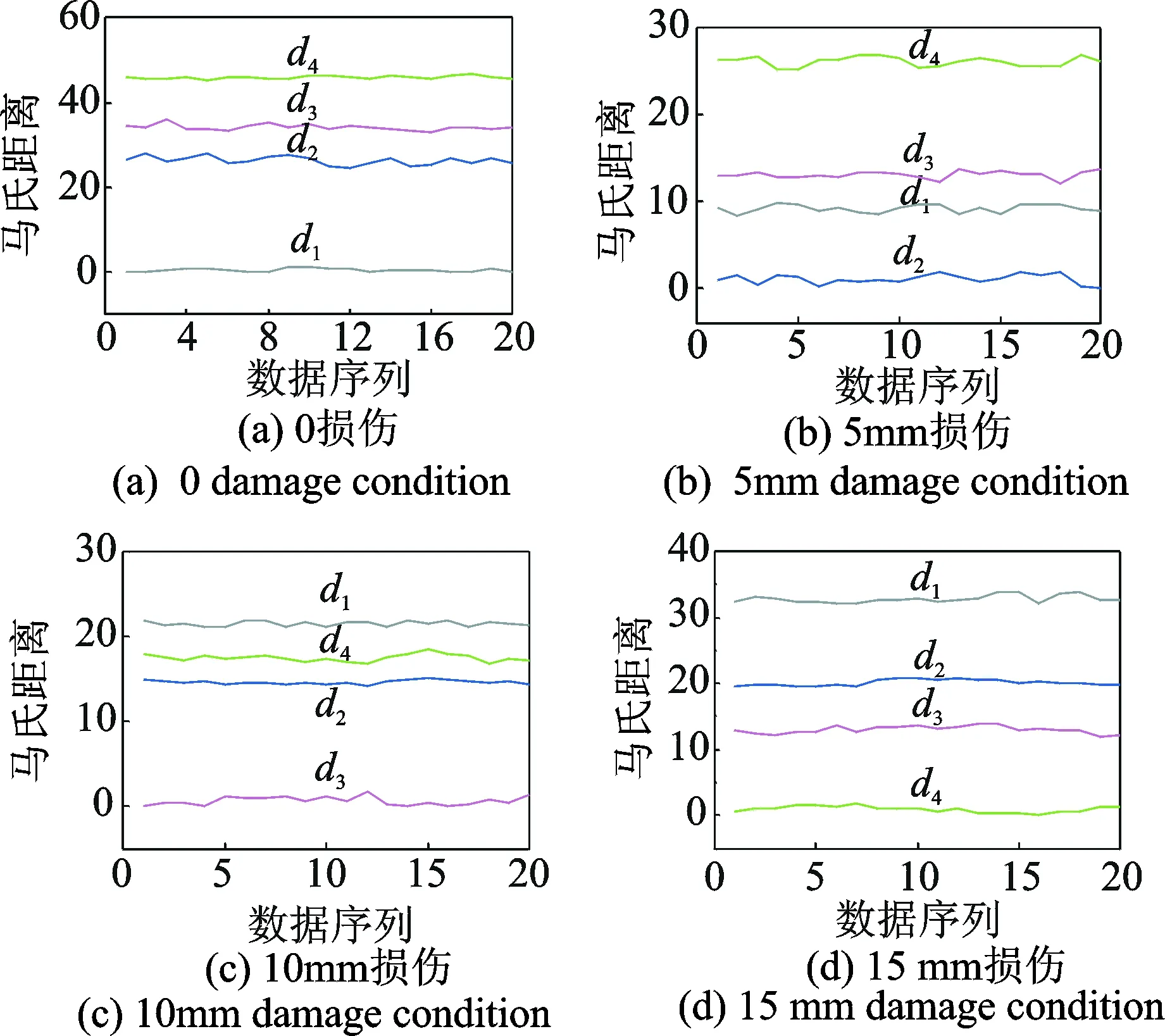
图9 马氏距离诊断结果Fig.9 Diagnosis results of Mahalanobis distance

为进一步验证VMD-HHT方法的有效性,在相同的试验条件下设置3测点20mm损伤工况进行试验研究。该工况随机选取20组样本信号按照上述方法和过程进行降噪、信息融合及边际谱处理,并对其进行马氏距离分析,如图10所示。可以看出,20mm损伤工况下,其相应的马氏距离d5均小于d1,d2,d3和d4,且有d5 图10 20mm损伤工况马氏距离诊断结果Fig.10 Diagnosis results of Mahalanobis distance under 20mm damage condition 1) VMD作为一种非平稳信号分析方法,具有分解效率高、自适应好及鲁棒性高等特点,有效克服了EMD,EEMD等方法缺乏严格的数学理论、计算效率低和模态混叠现象严重等缺点,分析结果更可靠,对泄流激励下水工结构振动信号具有较强的适用性。 2) 基于VMD边际谱提出了一种新的损伤特征向量-损伤灵敏指数Q,该指标能够有效反映结构振动信号的边际谱特征,提取水工结构的状态信息。不同工况下结构的损伤灵敏指数存在明显差异,随着损伤程度的增加,损伤灵敏指数也随之增大,从而有效区分结构的不同运行状态。 3) 将马氏距离引入水工结构损伤诊断领域,有效提取结构的损伤特性,准确识别结构的损伤和运行状态,实现泄流激励下的水工结构损伤诊断,且效果显著、精度较高。该方法为水工结构在环境激励下的损伤诊断供了新思路,为结构的运行状态评价提供了依据,应用前景广阔。 4) 该方法虽然能够准确识别结构的运行状态,实现泄流激励下的水工结构损伤诊断,但由于该损伤检测方法属于局部检测,需要事先对结构的受力及损伤破坏规律有一定的先验认识,以便在恰当的位置布置拾振器。因此,将VMD-HHT和有效的损伤定位方法结合,实现结构的损伤定位有待进一步研究。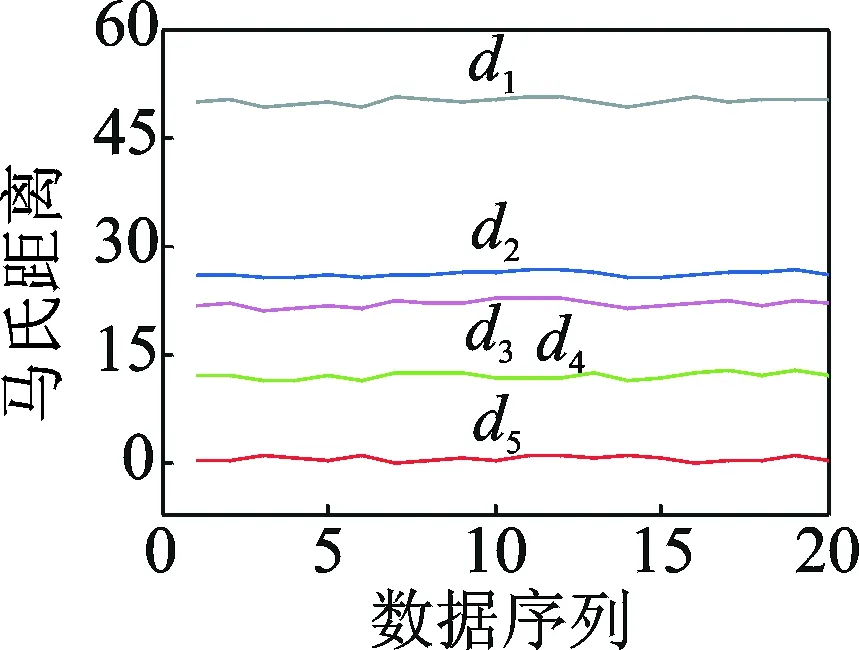
4 结 论

