大跨斜拉桥纵向地震碰撞响应参数分析
刘秀珍
(山西省交通科学研究院,山西 太原 030006)
桥梁结构的碰撞问题是桥墩及基础平面挠曲振动在墩顶的位移超过梁间伸缩缝宽度造成[1-2]。地震波激励在传播方向上经历地质和路径的不同,势必会造成桥梁地震响应特征值的不同。由此造成梁体碰撞的主动碰撞体有所差异。在此基础上,相邻联梁段自身周期大小和周期比被认为是影响碰撞效应的重要参数。周光伟等[3]对行波输入下连续梁桥不同周期的墩梁相对位移碰撞效应进行了分析,指出当周期比较小(T1/T2<0.5)时,碰撞效应最大,当周期比较大(T1/T2>0.7)时,碰撞效应较大,而介乎中间的周期比的碰撞效应则较小。王军文等[4]对相邻梁体的周期比、基本周期大小、相邻联的质量比、伸缩缝间隙大小以及墩柱的弹塑性等因素进行了分析,但仅针对结构形式较简单的梁桥分析,没有考虑大跨径斜拉桥结构特点对碰撞响应的影响。李建中等[5]也对桥梁碰撞方面进行了深入的研究,取得了一定的研究成果。邓玉林等[6]提出主引桥极易发生碰撞,碰撞不仅会产生很大的撞击,而且使引桥地震力需求、引桥梁端位移以及引桥梁体搭接长度需求有较大增长,但没有考虑主引桥周期比这一影响地震碰撞反应的主要因素。
针对上述情况,本文考虑地震波传播的方向性,基于主引桥周期不一致而表现出的动力特性差异,建立主引桥伸缩缝处碰撞效应非线性计算模型。以一座大跨斜拉桥与左右引桥地震碰撞响应为例,研究了纵向地震作用下主引桥碰撞效应影响规律,为桥梁的抗震安全性评估和抗震设计提供一定的参考。
1 计算模型
本文选取一座双塔面漂浮体系斜拉桥为代表进行相关研究。该桥桥跨布置如图1所示,跨径组合为左右对称形式,具体为45+67+416+67+45=640 m,左右引桥均为4×40 m等截面预应力混凝土箱梁结构。
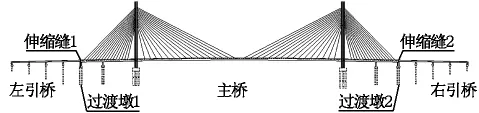
图1 桥梁总体布置图
为便于分析周期比对主引桥碰撞响应规律的影响,主引桥的碰撞问题简化为主动碰撞杆件一端正面垂直撞击平整刚性杆件(靶体)问题。其中,将左引桥、主桥和右引桥分别拟化为弹性杆件1、弹性杆件2和弹性杆件3,引入等效弹簧刚度的概念,桥墩对主梁的抗推刚度等效为一定刚度的弹簧。
为方便推导,对下列符号作如下说明:kc1为左引桥等效弹簧刚度;kc2为主桥等效弹簧的刚度;kc3为右桥等效弹簧的刚度;kt为伸缩缝碰撞弹簧的刚度;l1为左引桥等效杆件长度;l2为主桥等效杆件长度;l3为右引桥等效杆件长度[7-8]。假设主引桥具有相同的截面形式A、质量密度ρ和杨氏模量E;主动碰撞杆件的弹性波速和被动碰撞杆件中压缩弹性波的传播速度均取

设定碰撞弹簧刚度远大于引桥等效弹簧刚度,由系统运动微分方程组
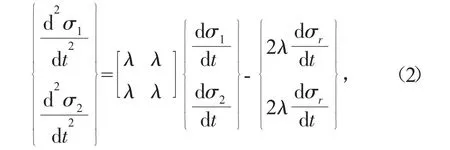
根据波阵面的动量守恒条件,主动碰撞体碰撞前为向靶体运动V0,即右行波。而碰撞瞬间,碰撞体的运动速度由两部分组成:a)碰撞端部由于接触应力的作用而引起的向左方后退速度为c,即左行波。b)左行波波面的前方是无应力区,在接这个区域的材料仍以原速度v0向靶体运动。靶体由接触应力的作用而引起的向右方后退速度为v1,则:

左右两侧同时乘以ρc,根据波动面的动量守恒条件

式中:σ1=ρcv为弹簧固有频率平方1,为弹性撞击后,碰撞体和靶体之间的接触应力;
σ0=ρcv0,为碰撞体仍以原速度v0运动部分产生的应力;
σl=ρcc,为以声速c由碰撞接触端沿左方向传播产生的应力。
由于本文仅考虑主引桥周期比对桥梁碰撞力峰值和位移峰值的影响,忽略弹塑性交界面对梁体影响,碰撞后主碰撞体以左行波速度移动,式(4)简化为:
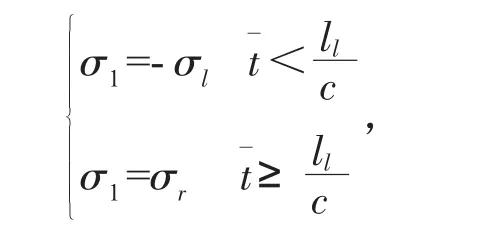
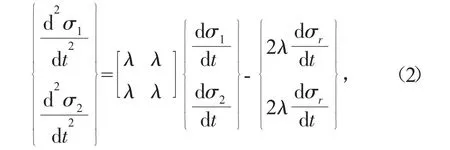
由杆件的基本周期T=2l/c,周期比可等效为:
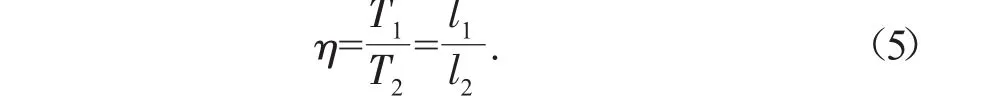
1.1 左引桥为主动碰撞体,主桥为靶体
a)η≤0.5 时(即 l2>2l1),σ2被认为始终是右行波,
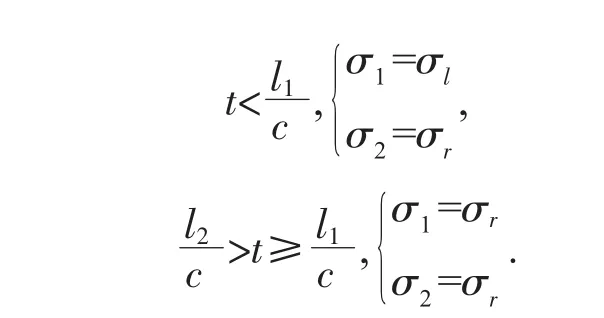
b)1≥η>0.5 时(即 2l1≥l2>l1),
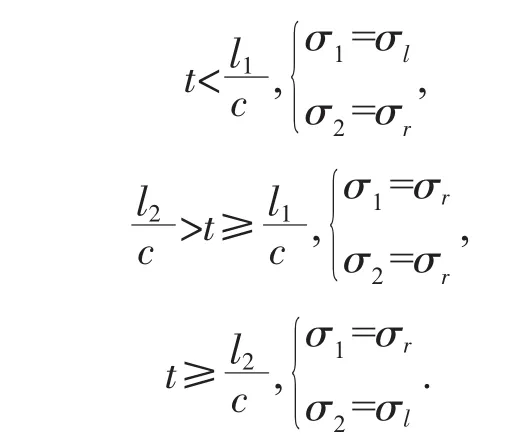
1.2 主桥为主动碰撞体,右引桥为靶体时,周期比η′=T2/T3
a)η′≤0.5 时(即 l2>2l3),
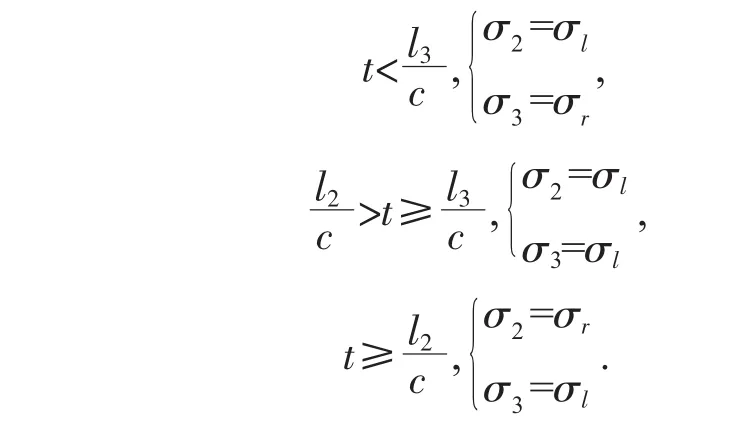
b)1≥η′>0.5 时(即 2l3≥l2>l3),
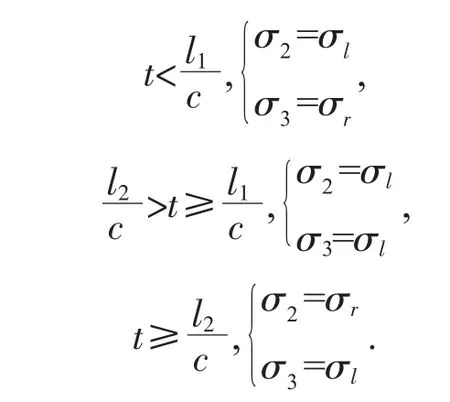
主引桥间碰撞弹簧采用接触单元模拟。碰撞刚度取较短主梁纵向刚度[6],恢复系数e取为1.0,即不考虑碰撞过程中的能量耗散。左引桥、主桥和右引桥的质量分别记为m1、m2和m3,基本周期记为T1、T2和T3,伸缩缝阻尼分别记为c1和c2,阻尼系统采用Rayleigh阻尼进行线性和非线性时程分析,伸缩缝间隙均为gp。具体如图2所示。
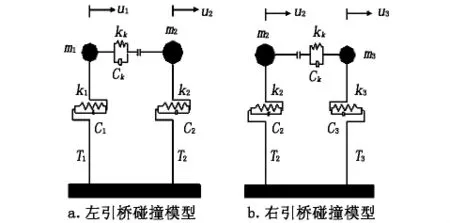
图2 简化碰撞模型
1.3 主引桥碰撞过程存在的模式
考虑地震波的行波效应,行波速度方向的差异会导致主引桥的碰撞过程存在不同的模式,具体可分为:
a)工况1 以图2a所示的动力计算模型考虑左引桥为主动碰撞体,该模型忽略右引桥的影响,只考虑左引桥与主桥之间的碰撞作用。
b)工况2 不考虑主桥与左引桥伸缩缝处的碰撞效应,简称左引桥无碰撞。
c)工况3 以图2b所示的动力计算模型考虑主桥为主动碰撞体,该模型忽略左引桥的影响,只考虑右引桥与主桥之间的碰撞作用。
d)工况4 不考虑主桥与右引桥伸缩缝处的碰撞效应,简称右引桥无碰撞。
2 地震波输入
为分析地震作用下的桥梁响应规律,选取了4条不同加速度时程从而分析碰撞效应对桥梁抗震性能的影响。
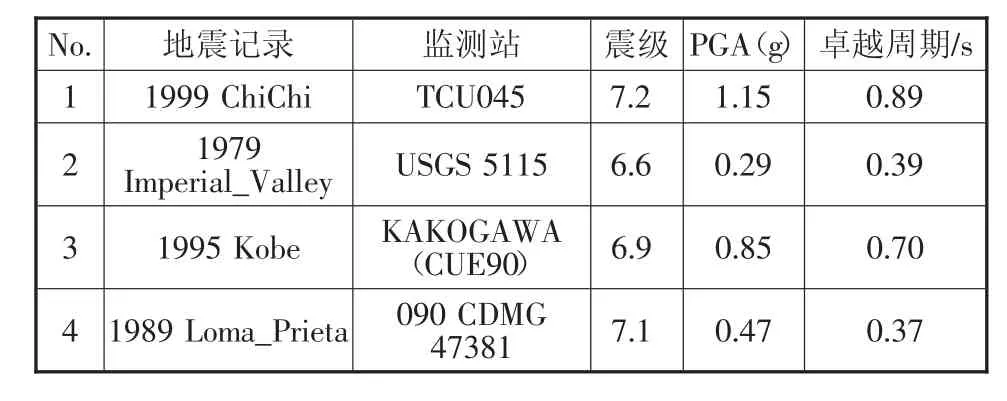
表1 选取的地震波
3 碰撞效应对桥梁抗震性能的影响
3.1 考虑碰撞效应对主桥的影响
图3、图4给出了工况1作用下考虑碰撞效应时主桥索塔塔顶位移比、索塔根部弯矩比随周期比变化曲线。
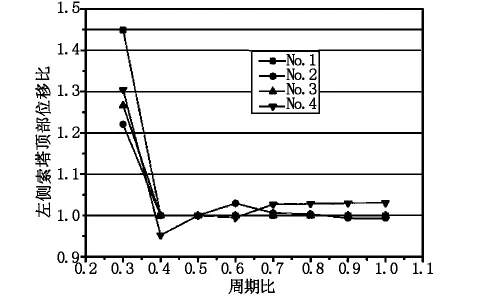
图3 左侧索塔塔顶相对位移比
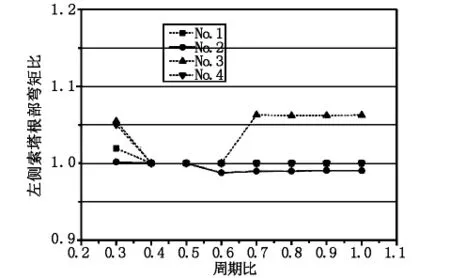
图4 左侧索塔根部弯矩比
由图3可知,引桥对主桥的单边碰撞效应导致索塔塔顶产生位移,左引桥基本周期T1越低,碰撞效应对索塔塔顶位移影响越大,但随着周期比T1/T2的增加,碰撞效应的影响整体趋于减小,这也验证了周期比是影响长周期桥梁地震碰撞效应的主要因素。由图4可知,左引桥基本周期T1越低,碰撞效应对索塔根部弯矩的影响越大,这与索塔顶部位移趋势保持一致。但随着周期比T1/T2的增大,碰撞效应影响趋于复杂,索塔根部弯矩比有可能增大(如地震波No.3的影响曲线),也有可能减少,但增幅不大,整体上保持碰撞效应不断减小的趋势。因此,地震作用下的碰撞效应对大跨径斜拉桥的影响较小,不会造成主桥结构地震需求的明显增大。
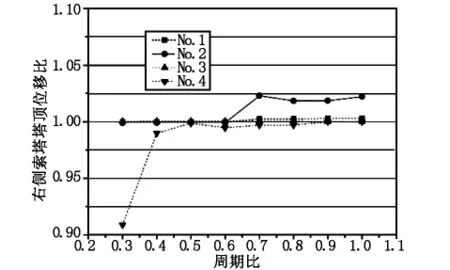
图5 右侧索塔塔顶相对位移比
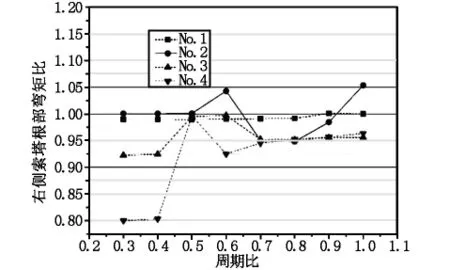
图6 右侧索塔根部弯矩比
图5、图6则给出了工况3作用下考虑碰撞效应时主桥索塔塔顶位移比、索塔根部弯矩比随周期比变化曲线。对比图3、图4的变化曲线,工况3作用下主桥的碰撞效应影响较工况1时偏小,索塔塔顶位移比和根部弯矩比影响虽然也有所增大,但增大幅度小于工况1。特别是当周期比T1/T2<0.5时,索塔塔顶相对位移比和根部弯矩比均小于1,此时碰撞效应反而减小地震导致的塔顶位移和索塔根部弯矩。因此,工况1和工况3两种不同碰撞模式对主桥抗震效应会产生不同的影响,工况1影响效果大于工况3。
3.2 考虑碰撞对引桥的影响
图7给出了工况1和工况3作用下伸缩缝处碰撞力峰值的比较图。图7表明,即使相同地震波作用下,不同主动碰撞体发生的单边碰撞,产生的碰撞力峰值也会存在差异。工况3作用下碰撞过程更易激起较大的碰撞力,从而引起结构的震害也更为严重。这种差异表现将随着地震波有效加速度峰值和持续时间的增大而增大。由于大跨径斜拉桥的主梁质量大于引桥梁体,则在惯性作用下的碰撞强度加大,产生的碰撞力峰值也较大。
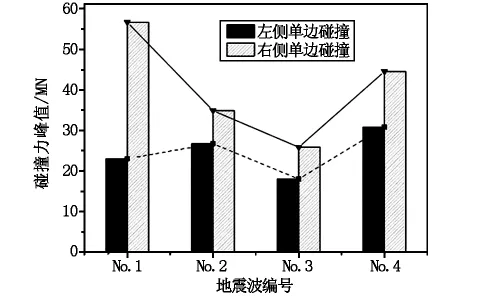
图7 伸缩缝处碰撞力峰值曲线
图8、图9给出了工况1作用下,考虑碰撞效应时左引桥梁端相对主桥位移比和梁端位移比的变化曲线。
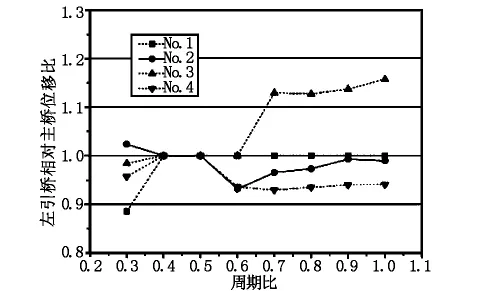
图8 左引桥相对主桥位移比曲线
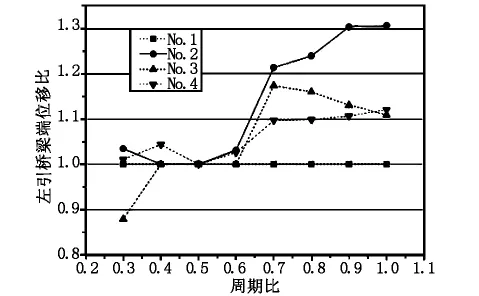
图9 左引桥梁端位移比曲线
由图8可以看出,在地震作用下,考虑引桥与主桥的周期比差异,不同纵向地震波引起伸缩缝处的非同向振动,形成引桥与斜拉桥主桥梁体相对位移的变化。单边碰撞有时增大引桥梁端相对主桥位移,有时减小引桥梁端相对主桥位移,但总体影响不大。图9则表明单边碰撞作用下,左引桥梁端-过渡墩间的距离整体上随着周期比的增加而增加。具体来说,当周期比T1/T2<0.5时,碰撞效应影响不大,但当T1/T2>0.5,碰撞效应则会使得左引桥梁端位移明显增大,且碰撞效应对梁端位移影响随周期比的增大而增大。
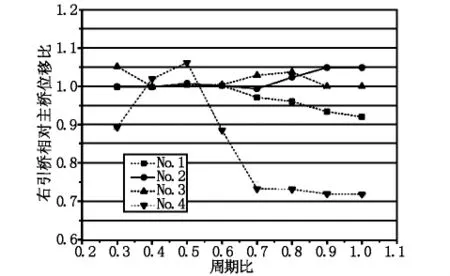
图10 右引桥相对主桥位移比曲线
图10、图11分别给出了工况3作用下右引桥梁端相对主桥位移比和梁端位移比的变化曲线。由图12和图13可以看出,当T3/T1<0.5时,碰撞效应对引桥梁端相对主桥位移比和梁端位移比影响不大。当T3/T1>0.5时,总体上梁体碰撞效应随主引桥周期比的增加而减小,但幅度变化不大。对比工况1和工况3对应的梁端相对主桥位移比和梁端位移比曲线可以发现,引桥单边碰撞与主桥单边碰撞呈现完全相反的结果,引桥单边碰撞效应明显大于主桥单边碰撞效应,这也说明碰撞效应的不同源于地震波的纵向传播方向的不同。
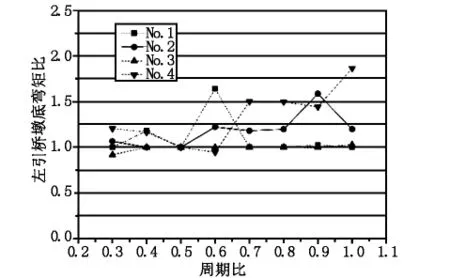
图12 左引桥墩底弯矩比曲线
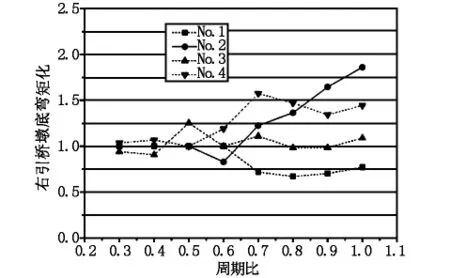
图13 右引桥墩底弯矩比曲线
由图12和图13可以看出,考虑单边碰撞作用,总体上将使引桥墩底地震响应增大,但增加幅度较小,相比较而言,工况1作用下墩底响应整体上随周期比的增大而增大,而工况3作用下的引桥影响规律较为复杂,随周期比的增加,碰撞效应的比值可能增加,也可能减小,这与地震波有效加速度峰值和持续时间有关。
4 结论
a)引桥基本周期T1越低,碰撞效应对索塔影响越大,但随着周期比T1/T2的增加,碰撞效应的影响整体趋于减小。
b)主桥为主动碰撞体的碰撞效应会对增加主桥抗震位移和弯矩参数需求,但增大幅度小于引桥为主动碰撞体的碰撞效应,即后者的影响效果大于前者。
c)即使相同地震波作用下,不同主动碰撞体发生的单边碰撞,产生的碰撞力峰值也会存在差异。主桥为主动碰撞体的碰撞过程更易激起较大的碰撞力,从而引起结构的震害也更为严重。这种差异表现将随着地震波有效加速度峰值和持续时间的增大而增大。
d)引桥单边碰撞与主桥单边碰撞在梁体位移影响上呈现完全相反的结果,引桥单边碰撞效应明显大于主桥单边碰撞效应,这也说明碰撞效应的不同源于地震波的纵向传播方向的不同。

