中子星质量分布与诞生方式的研究∗
刘 鹏张 洁支启军
王德华2,3尚伦华2,3杨佚沿4潘元月5
(1西华师范大学物理与空间科学学院南充637009)
(2贵州师范大学物理与电子科学学院贵阳550001)
(3贵州省射电天文数据处理重点实验室贵阳550001)
(4贵州师范学院物理与电子科学学院贵阳550018)
(5湘潭大学物理与光电工程学院湘潭411105)
1 引言
1967年Jocelyn Bell与Antony Hewish发现了第一颗脉冲星PSR B1919+21,后被认证为中子星(NS)[1].目前总共发现有2700多颗NS[2],其中有72颗NS已测得质量.一般认为,NS是大质量恒星演化末期超新星爆发形成,依靠中子简并压以及核力来平衡自身引力.NS因其超高的密度和强引力为研究核物理和广义相对论提供了天然的实验室[3−6].质量是NS重要的参数之一,包含着丰富的物理信息:不仅可以反映出中子星的结构、核物质成分及其物质的状态方程,而且能推断超新星的爆发机制、NS前身星演化途径,揭示致密双星的吸积演化[7−9].
1994年Finn首先对4个双中子星(DNS)系统运用Bayesian统计方法,得到NS质量主要分布在1.3−1.6 M⊙[10].1999年Thorsett和Chakrabarty对19颗NS的质量进行统计研究,发现NS的质量分布与高斯分布一致,峰值在(1.35±0.04)M⊙[11].2010年Schwab等人认为DNS中的NS质量分布实际是双峰结构,一个峰值在1.245 M⊙,另一个峰值在1.345 M⊙,并将其归因于不同的超新星爆发机制[12].2011年Zhang等人对46颗NS的质量统计研究表明,NS的平均质量为(1.46±0.30)M⊙[13].另一方面,Zhang等人基于NS自旋周期和伴星,将中子星分成不同种类,推断出各个子群的质量分布,发现经历了显著吸积过程的NS质量要比没有经历过的NS质量大∼0.2 M⊙,并估计出再生NS的吸积质量与自旋周期之间的关系为△M=0.43(Ps/ms)−2/3[13].Valentim等人和Kiziltan等人发现NS质量呈双峰分布,这表明中子星有两种形成机制和演化过程[14−15],Alsing等人进一步验证了质量双峰分布的正确性[16].¨Ozel等人运用Bayesian统计方法研究不同双星中NS质量的分布,并预测了通过超新星捕获电子后塌缩形成的NS,其诞生质量在1.06−1.22 M⊙[17].Cheng等人研究发现,高质量X射线双星(HMXB)与DNS的质量分布存在相似平均值,分别为(1.340±0.230)M⊙和(1.335±0.055)M⊙,这表明DNS可能产生于HMXB[18−19].杨佚沿等人研究发现DNS中主、伴星质量趋于均匀化,可能源于密近双星相互作用[20−22].
近年来已测量质量的NS数量显著增加,使我们能够更加详细地统计研究NS的质量分布.我们统计72颗NS的质量,运用Monte-Carlo方法对NS质量进行模拟,以此来充分考虑质量测量的不确定度.本文的重点是统计分析NS的质量分布,并结合NS的自转周期和表面磁场,进一步探究NS的演化途径.文章结构如下:第2部分介绍NS的质量及其相关参数,第3部分统计研究NS的质量分布,NS在磁场强度-自转周期图中的分布以及NS的质量与自旋周期的关系.第4部分我们对全文进行总结与讨论.
2 NS质量及相关参数
本文在表1和表2列出了72颗已知质量的NS及相应参数,参数包括NS质量M、伴星质量Mc、自旋周期Ps、自旋周期导数˙Ps、轨道周期Porb、磁场强度B和轨道偏心率e,在最后还列出了完整的参考文献.在表1中,我们列出了11对HMXB、5对低质量X射线双星(LMXB)、2对X射线双星(XB)、9对DNS和4对中子星主序星系统(NSMS).在表2中,我们列出了32对中子星白矮星系统(NSWD).从表1–2中发现质量最大和最小的NS分别是:J1748-2021B((2.74±0.22)M⊙)和2A 1822-371((0.97±0.24)M⊙).为了更加直观地展现出NS质量,我们给出72颗NS的质量图,如图1.
目前NS质量的测量可分为两类:射电脉冲星的质量测量和X射线脉冲星质量的测量.从表1–2中可以看出由于NS类型不同,质量测量的精度也有所区别.DNS因其离心率大,相对论效应明显,所以DNS可以精确测量NS质量[18−19].在DNS系统PSR 1913+16中首次精确测量到NS的质量[23].毫秒脉冲星其偏心率小,相对论效应不明显,导致测量质量误差较大.X射线NS的测量误差大约为质量的10%.
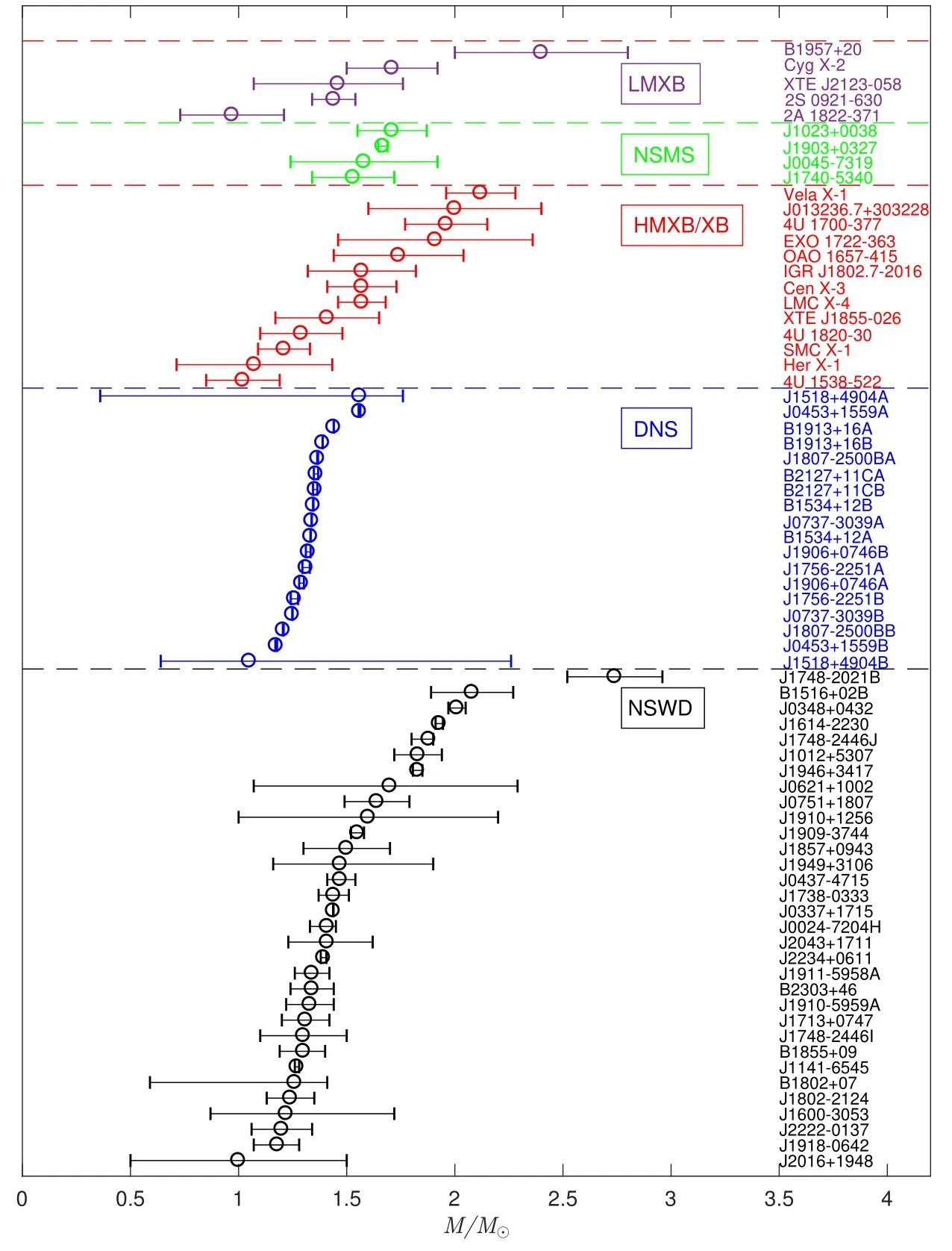
图1 中子星质量图.NSWD、DNS、HMXB/XB、NSMS、LMXB分别用黑色、蓝色、红色、绿色、紫色表示.Fig.1 The picture of neutron star masses.The black,blue,red,green,and purple represent NSWD,DNS,HMXB/XB,NSMS,and LMXB,respectively.
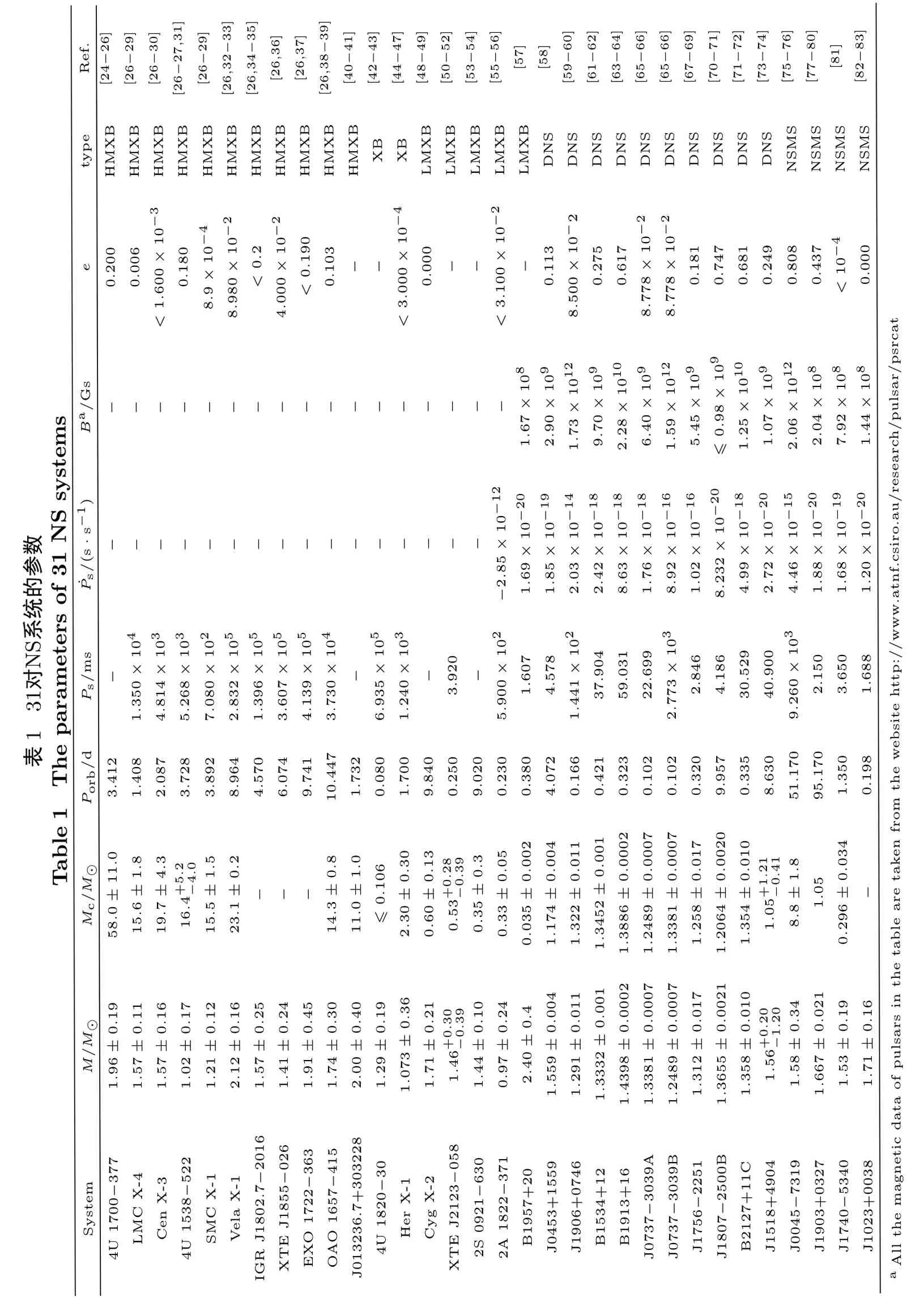
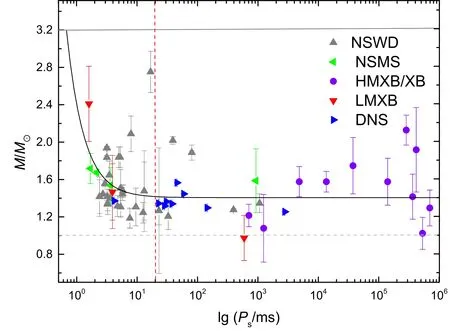
表13aram1对NS系统的f3参Table1Thepeterso数1NSsystemsSystemM/M⊙Mc/M⊙Porb/dPs/ms ˙Ps/(s·s−1)Ba/Gs e typeRef.4U1700−3-4771.96±0.1.1.1.1.1.1.2.2.4.3.4.19 1 6 7 2 6 5 4 5 0 0 9 58.0±11.0 3.412−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−×10.200 HMXB[24−26LMCX1.57±015.6±1.81.408 1.35−0×104 0.006 HMXB[26−29]]CenX-31.57±019.7±4.32.087 4.814×103<1.600×10−3HMXB[26−30]4U1538−5221.02±016.4+5.2.0−43.728 5.268×103 0.180 HMXB[26−27,31]SMCX-11.21±015.5±1.53.892 7.080×102 8.9×0×0.2 1010−4HMXB[26−29]VelaX-1 2.12±023.1±0.28.964 2.832×105 8.98−2HMXB[26,32−33]IGRJ1802.7−2016 1.57±0−−−±04.570 1.396×105 232 NSWD统2N参数SWTable2Th表eparam对eterso系f3DsystemsSystemM/M⊙Mc/M⊙Porb/dPs/ms ˙Ps/(s·s−1)Bb/Gs e typeRef.J0437−47151.44±0(.07 0.24±0(.0175.741 5.760 5.73×10−205.81×1081.918×10−5NSWD[84−86J0621+10021.70+0.59−0.63+0.32−0.29)0.97+0.43−0.2+0.27−0.15)8.320 28.9004.73×10−201.18×1093.000×10−3NSWD[87−88]]J0751+18071.64±0.1.1.0.15 1 1 1 0.19±0.0.0.01 2 1 0.263 3.479 7.79×10−211.67×1083.300×10−6NSWD[89−90J1012+53071.83±00.16±00.604 5.256 1.71×10−203.04×1081.300×10−6NSWD[91−92]]J1141−65451.27±01.02±00.010.198 3.940×103 4.31×10−151.32×1012 0.172 NSWD[93−94J1713+07471.31±00.286±2 67.8304.750 8.53×10−212.00×1087.500×10−5NSWD[95−96]]B1802+071.26+0.15−0.67 0.36+0.67−0.15 2.620 23.1004.67×10−193.32×1090.212 NSWD[97−98B1855+091.30+0.10−0.11 0.263+0.013−0.011 12.3275.360 1.78×10−203.13×1082.163×10−5NSWD[99−10]0]J1909−3+3746441.55±0.0.13 0 0.213±0.002 1.533 2.950 1.40×10−202.06×1089.200×10−8NSWD[99,101]B2301.34±01.3±0.1012.3401.066×103 5.69×10−167.88×1011 0.658 NSWD[102−103]J1738−03331.47+0.0.07 6−00.81+0.0.007−0050.354 5.850 2.41×10−203.80×1081.100×10−6NSWD[104]J1614−22301.928±±00.014 4 7 0.493±0.003 3 8.687 3.151 9.62×10−211.76×1081.333×0×1010−6NSWD[99,105]J0348+04322.01.0.10.172±±00.006 0.102 39.1232.41×10−193.11×109<8.10−5NSWD[106−107]J2222−01371.20±00.011.05.02.446 32.8185.87×10−201.40×1093.801×10−4NSWD[108]J2234+06111.393±3 0.275±0.0832.0013.600−−×10.129 NSWD[109]J1949+31061.47+0.43−0.31 0.85+0.14−0.11 1.950 13.1389.39×10−201.12094.290×10−5NSWD[99,110]J1802−21241.24±0.1.01 8 0.78±0.0.04 2 0.699 12.6487.26×10−209.69×1082.480×1010−6NSWD[111]J1911−3+59175811A 1.34±00.18±00.860 3.270 2.95×10−219.93×107<−5NSWD[112−113]J2041.41+0.2.11 8−00.177+0.0.017−0151.482 2.400 5.24×10−211.13×1084.890×10−6NSWD[82]J0337+17151.4378±00.02.0012 3 0.19751±±00.0001019 5 1.629 2.733 1.77×10−202.22×1083.536×10−2NSWD[114−115]J1946+34171.828±0.2656.027.0203.170 3.12×10−211.01×1080.134 NSWD[107]J1918−06421.18+0.1−0.1 1 0.219+0.012−0.011 10.9137.600 2.57×10−204.49×1082.034×10−5NSWD[99,116−117]J0024−720446H I J 1.41+0.04−0.08 0.18+0.086−0.016 2.358 3.210−1.84×−−10−21−−−7.056×10−2NSWD[118−120]J1748−241.3±0.020.241.328 9.570 0.428 NSWD[121]J1748−24461.88+0.02−0.08 0.381.102 80.3400.350 NSWD[122]J1748−6+200221B B 2.74±0.2.12 9>0.1120.55016.760−3.2.39×10−1− − ×10.570 NSWD[122,113]B1512.08±00.5.1>0.136.858 7.947−33×10−29 1 0.138 NSWD[123−124]J2016+19481.0±±00.43−00.01.47 635.024 64.9404.01×10−195.16091.480×10−3NSWD[123]J1910−0−593059A 1.331 0.180±8 0.837 3.266 2.95×10−219.93×1073.000×10−6NSWD[125]J160531.22+0.5−0.3 5 0.21+0.06−0.04 14.3483.598 9.50×10−211.87×1081.737×10−4NSWD[74]J1910+12561.6±0.6 0.30−0±312.34 58.4674.984 9.68×10−212.22×1082.302×10−4NSWD[122]J1857+09431.5±0.2 0.25.3275.362 1.78×10−213.13×1082.174×10−5NSWD[99,113]bAllthemagneticdataofpulsarsinthetablearetakenfromthewebsitehttp://www.atnf.csiro.au/research/pulsar/psrcat. 目前我们在63对双星系统中收集到了72颗测得质量的NS.为了减小NS质量测量不确定度对统计结果的影响,我们使用蒙特卡罗方法模拟72颗NS的质量分布,然后基于模拟结果进行统计分析.如图2左图,统计后发现质量呈双峰分布,通过高斯拟合给出双峰位置分别为:(1.328±0.220)M⊙和(1.773±0.416)M⊙. 为了进一步确定NS的质量分布呈双峰结构的正确性,我们做出NS的质量分布累积曲线(cumulative distribution function,CDF).如图2右图,我们发现NS质量的累积曲线仍然呈现出双峰结构,峰值大约在1.3M⊙和1.8M⊙. 一般认为,NS是超新星爆发的产物,其理论质量约为1.4M⊙.根据吸积理论,在双星系统中,NS由于从伴星中吸积物质,使自身质量增加,使得NS质量大于1.4M⊙.为什么质量分布中有相当多的NS处于1.328M⊙,我们认为一种可能的解释是,NS的诞生除了超新星爆发这一途径外,还可能存在另一种诞生途径. 本文将18颗DNS单独做考虑,并对余下的54颗NS进行统计研究.如图3右图,我们可以发现:图中直方图并不连续可能是因为DNS数据点太少的缘故,而且DNS的质量分布没有明显的双峰结构,对其进行高斯拟合发现:一个高斯拟合效果最好,质量的平均值在1.330M⊙,标准差为0.0089M⊙. 我们发现DNS的平均质量小于NS的理论诞生质量.杨佚沿等人认为导致DNS质量较小的原因可能有两种:一种是双星系统中由于相互作用,导致恒星提前演化,形成质量较小的NS.另一种是DNS前身星是NS和质量小于8M⊙的恒星,在引力的作用下,恒星改变了演化路径直接形成小质量的NS[20−22]. 图3左图为剩余54颗NS质量分布直方图.从图中可以看出,在不考虑DNS后,其质量分布直方图表现出更加明显的双峰结构.对其进行高斯拟合后发现NS质量分别集中在(1.360±0.337)M⊙和(1.854±0.322)M⊙.由此可以看出,DNS对NS的质量分布影响较小,而且DNS质量的单峰分布意味着DNS中的NS形成或演化历史可能不同于其他双星系统. 图3 54颗去除DNS的NS质量分布直方图(左)和18颗DNS质量分布直方图(右).图中实线是复合拟合,虚线是单高斯拟合.左图得到两个峰值分别是(1.360±0.337)M⊙和(1.854±0.322)M⊙.右图峰值在(1.330±0.0089)M⊙.Fig.3 Histograms of mass distribution of 54 neutron stars removed the DNS(left)and 18 DNS(right).In the diagram,the solid line is a compound Gauss fitting,and the dashed line is a single Gauss fitting.The left panel shows two peaks:(1.360±0.337)M⊙and(1.854±0.322)M⊙,respectively.The peak of right panel is(1.330±0.0089)M⊙. 人们普遍认为NS诞生时自旋周期(Ps)较慢,在双星系统中NS不断从伴星吸积物质,而使自旋不断加快,在吸积到足够的物质后,Ps可达毫秒量级.因此如果质量与吸积间存在这种关系,我们就可能在不同的自旋周期范围内的NS质量统计中看到,周期越小其平均值越大. 本文将53颗有测量周期的NS在20 ms处分为两类,即31颗毫秒中子星(MSP,Ps6 20 ms),30颗正常中子星(PSR,Ps>20 ms).然后分别对这两类NS的质量进行统计研究,如图4.我们发现MSP与PSR的质量分布都呈现出双峰结构,通过高斯拟合出峰值分别位于(1.396±0.313)M⊙和(1.860±0.231)M⊙、(1.301±0.083)M⊙和(1.517±0.407)M⊙.我们得到MSP双峰值都大于PSR的双峰值,平均大∼0.22M⊙.这与NS吸积加速的假设一致,表明NS在诞生后吸积∼0.22M⊙的物质时,可能成为MSP. 为了进一步研究NS演化历史和形成条件,我们分析了1颗LMXB、4颗NSMS、10颗DNS、27颗NSWD在磁场强度-自旋周期(B-Ps)上的分布.如图5所示,我们可以看出:NS磁场强度主要分布在108−1012Gs之间,其中毫秒PSR区域的NS其B在108−109Gs之间,正常PSR区域内的NS其B在1012Gs周围,即如果我们假定NS的诞生磁场为1012Gs,那么通过吸积其磁场强度将衰减到108−109Gs.我们还可以发现质量M>1.4M⊙和M<1.4M⊙的NS都具有完整的演化过程,这表明NS诞生方式除了铁核塌缩超新星爆发外,还可能存在另一种诞生机制,使其初始质量小于1.4M⊙. 图4 30颗PSR质量分布直方图和31颗MSP质量分布直方图.其双峰峰值分别为:(1.301±0.083)M⊙和(1.517±0.407)M⊙、(1.396±0.313)M⊙和(1.860±0.231)M⊙Fig.4 Histogram of 30 measured PSR masses(left)and histogram of 31 measured MSP masses(right).Its bimodal peaks are:(1.301±0.083)M⊙and(1.517±0.407)M⊙,(1.396±0.313)M⊙and(1.860±0.231)M⊙,respectively. 图5 42颗NS的B-P s图.灰色点、三角形、正方形、圆形、五角形分别表示PSR、DNS、NSWD、NSMS、LMXB(实心和中空分别为M>1.4M⊙和M<1.4M⊙的NS).灰色虚线为P s=20 ms.Fig.5 The diagram of the surface magnetic field strength versus spin period for 42 NS.The gray point,triangle,square,circle,and star represent PSR,DNS,NSWD,NSMS,LMXB(Solid and hollow are NSM>1.4M⊙andM<1.4M⊙,respectively).The gray dotted line isP s=20 ms. 为了探究NS质量与自旋周期的关系,本文将53颗NS按不同的种类画在M-Ps图中,包含9颗HMXB、2颗XB、3颗LMXB、9颗DNS、30颗NSWD.如图6所示,可以看出红色虚线左方的快速NS,其质量总体上随周期的减小而增大,黑色曲线为拟合的NS质量和自旋周期之间关系,拟合函数为: 而且,随着HMXB数据点的增多,我们发现其质量与周期似乎也表现出一定的幂律关系,本文暂不做讨论. 图6 53颗NS的质量与自旋周期图.紫色圆、红色倒三角、蓝色右三角、灰色三角、绿色左三角分别表示HMXB/XB、LMXB、DNS、NSWD、NSMS.灰色虚线为M=1.0M⊙代表最小可被探测的NS质量,灰色水平实线为M=3.2M⊙代表可被探测的最大NS质量,垂直红色虚线为P s=20 ms.黑色曲线代表NS质量与自旋周期之间的关系.Fig.6 Diagram of mass versus spin period for 53 NS.The purple circle,red del,blue right triangle,gray triangle,and green left triangle represent HMXB/XB,LMXB,DNS,NSWD,and NSMS,respectively.The gray dotted line isM=1.0M⊙,which represents the smallest detectable NS mass,the gray horizontal solid line isM=3.2M⊙,which represents the maximum NS mass that can be detected,and the vertical red dotted line isP s=20 ms.The black curve represents the relationship between the NS mass and the spin period. 本文基于现有72颗NS的测量质量,研究了不同类型的双星系统和处于不同演化阶段的NS质量分布,我们获得以下推断和结论: (1)对72颗具有可靠质量测量的中子星,其质量分布呈双峰分布主要集中在(1.328±0.220)M⊙和(1.773±0.416)M⊙.这与Valentim等人和Kiziltan等人的NS为双峰分布结论一致[14−15].表明NS可能有两种诞生机制. (2)对18颗DNS的统计发现,其质量为单峰分布,平均值在1.330M⊙,标准差为0.0089M⊙.排除DNS后余下的54颗NS质量分布仍然呈现双峰结构,峰值分别为(1.360±0.337)M⊙和(1.854±0.322)M⊙. 由此可以看出,DNS对NS的质量分布影响较小,而且DNS质量呈单峰分布且其平均值小于理论诞生质量,这可能意味着DNS的质量形成或演化历史可能不同于其他双星系统. (3)我们发现MSP(Ps6 20 ms)与PSR(Ps>20 ms)的质量都为双峰分布,双峰分别位于(1.396±0.313)M⊙和(1.860±0.231)M⊙、(1.301±0.082)M⊙和(1.517±0.407)M⊙,而且MSP的平均质量比PSR的平均质量大0.22M⊙.这意味着NS吸积∼0.22M⊙的物质,可能成为MSP. (4)根据NS在B-Ps图上的分布,我们可以得到,在整体上,NS的磁场强度随周期的加快而衰减,而且发现对于质量M>1.4M⊙和M<1.4M⊙的NS都具有完整的演化过程,表明NS诞生方式除了铁核塌缩超新星爆发外,还可能存在另一种初始质量小于1.4M⊙诞生机制.根据NS在M-Ps图上的分布,我们拟合出NS质量和周期的关系为M=1.4+(Ps/ms)−3/2M⊙. (5)本文通过对NS的质量统计研究发现,NS可能存在两种诞生机制.我们认为这两种机制分别可能为: i:较高质量的NS,由铁核塌缩超新星爆发产生.一般认为对于质量在12−25M⊙的恒星,在恒星演化中,氢、氦、碳等元素可以充分燃烧,在演化末期形成铁核,当其超过钱德拉塞卡质量并没有更多的核燃烧时,铁核塌缩超新星爆发,于恒星中心形成质量约为1.4M⊙的NS. ii:较低质量NS,由电子俘获超新星爆发产生.对于8−12M⊙的恒星,由于恒星质量较小且温度不够高,核反应进行到Ne时停止,在演化末期形成一颗质量在1.1−1.37M⊙之间的O-Ne-Mg核白矮星(WD)[126−127].在双星系统中,由于吸积作用下WD的质量不断增加,当WD质量达到1.44M⊙的Chandrasekhar极限时,WD电子简并压将不足以平衡自身引力,20Ne电子俘获,WD将塌缩成一个质量约为1.25M⊙的NS[128−133].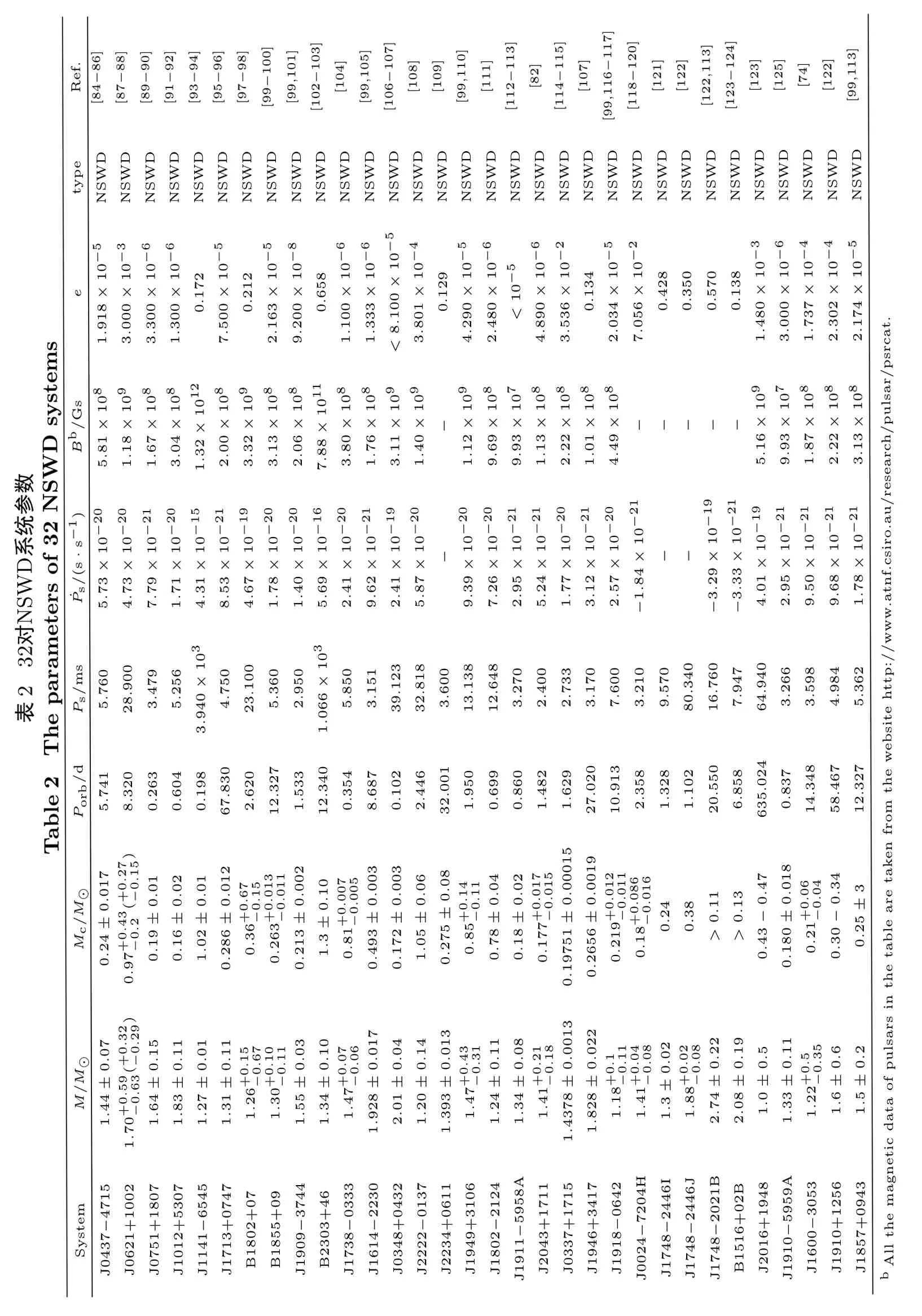
3 中子星质量的统计
3.1 DNS质量分布及其对NS整体的影响

3.2 MSP和PSR的质量分布
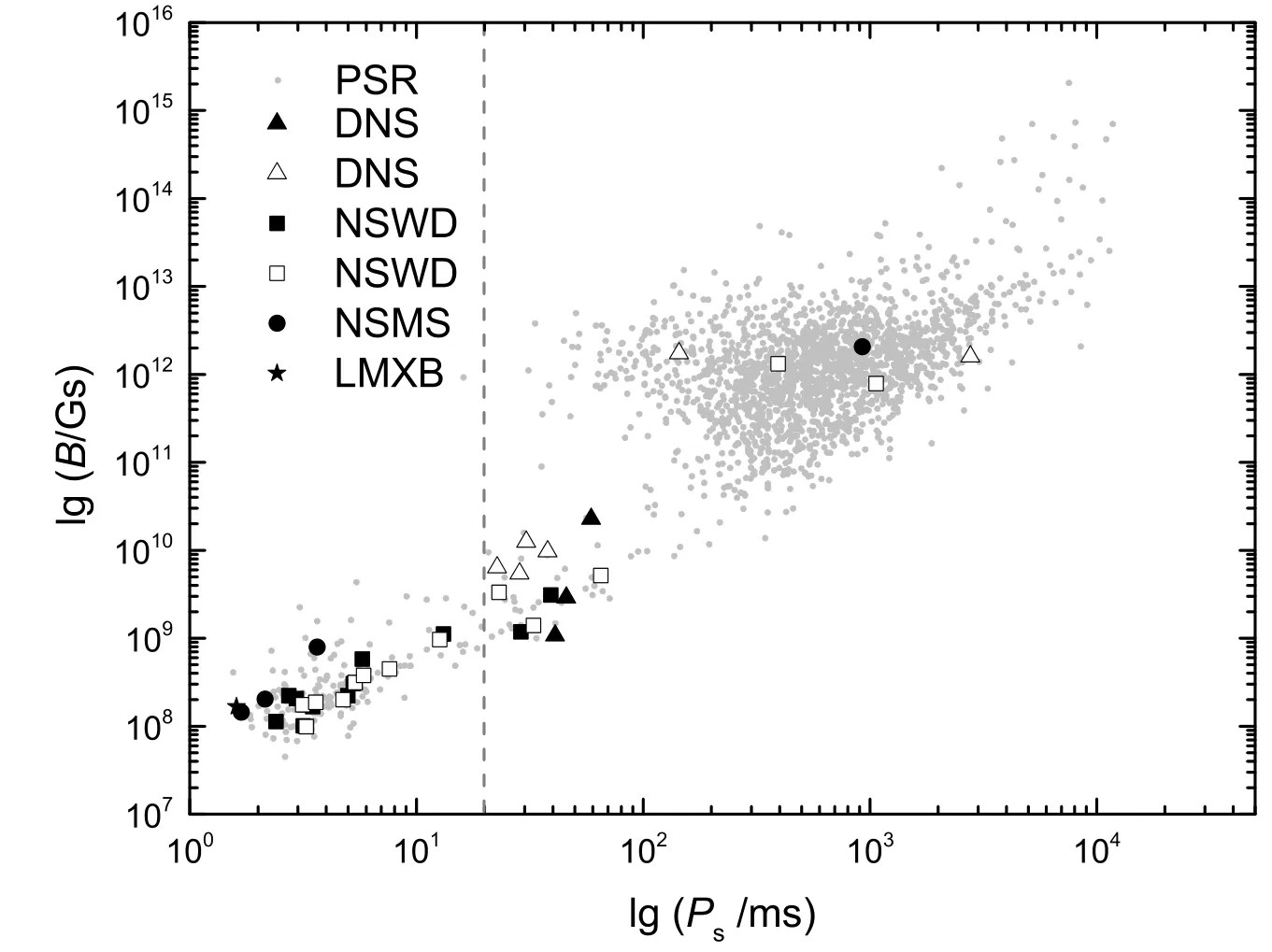
3.3 NS自转周期、磁场、质量之间的关系
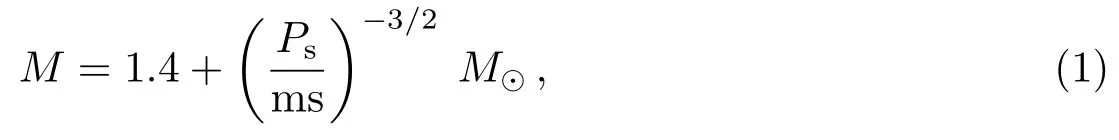
4 总结与讨论

