渗透模型思想 突破教学难点——以一年级“解决问题”教学为例

俞丁玲

在小学低段“解决问题”教学过程中，教师往往关注的是情境创设和信息收集，鼓励学生根据已有的生活经验解决问题。通过情境教学，激发了学生的学习兴趣，充分调动了学生学习的积极性，然而一堂课下来似乎还欠缺些什么。

如图1是一道学生非常容易出错的题，学生知道问题是求“左边被冰山挡住了几只？”也能口答：左边被冰山挡住了2只，但所写算式是这样的：2+4=6。

图1

师：说一说你是怎么理解这个题目的？

生：左边2只企鹅，右边4只企鹅，合起来一共有6只。

师：你是怎么知道“左边是2只企鹅”的？

生：左边肯定是2只，不然合起来就不是6只了。

通过访谈不难发现：学生是通过经验得到题目中左边的企鹅数的。为何学生无法获得准确的数学表达式呢？一方面，学生受前一课“加法”先入为主的影响，在“求总数”的负迁移下，认为应该把算式写成加法。另一方面，低年级学生以形象思维为主，分析和归纳能力有限，思考问题的方式比较简单，喜欢凭经验解决问题，缺乏对情境内容的归纳提炼和概括抽象，忽视对数量关系的分析，从而无法将现实问题的操作过程与数学算式联系起来。这就导致了学生数学思考的发展没有深度，解决问题的能力不足。

因此，我们在解决问题的教学过程中，不仅要关注学生对数量关系的分析，更要适当地渗透模型思想。那如何帮助一年级学生建立加减法模型呢？我从以下几方面进行了实践。

一、建立主干模型，准确审题

理解题目的意思在解决问题过程中非常重要，对学生能正确地作出解答有重要影响。而一年级学生受识字量和生活经验的限制，读题能力普遍较弱，教师应帮助学生从杂乱的图文信息中有效地提取有用信息。

1.读懂图文信息。

“读题”是沟通题意的第一步，审题正确与否直接决定了解决问题的方向与效果。学生先通过视觉在大脑中形成表象，再通过语言表述出来，才能促使学生真正地理解题意。在解决问题的教学中，尽量让学生用自己的话来表述题意，“说”的过程即是“悟”的过程，将数学语言内化为学生自己的认识，从而感悟其中的关系。

（1）简单图意说具体。

一年级教材中刚开始的图很简单，有的有故事情节，有的有数学信息。因此，只需要引导学生仔细观察，以小故事的形式，用“两个条件和一个问题”的句式描述图画的意思，为解决后续的图文问题打下扎实的基础。

（2）图文问题说清楚。

当出现图文问题时，主要有两种情况：一是图中和文字中都有信息，学生容易看清楚（如图2）；二是图与文字信息不完全匹配，但文字中有具体信息（如图3）。第二种情况对部分学生来说是有点糊涂的，这时教师就要及时引导学生把信息中的含糊部分说清楚。

图2

图3

2.区分条件与问题。

条件是解决问题的要素，问题则是方向。在解决问题过程中区分条件和问题也是审题的关键。低年级学生语言能力较弱，教师读题时应适当提取简洁的主干模型，引导学生有序地表达。

（1）“两个条件一个问题”，建立主干模型。

如图4“树上有3只松鼠，又来了2只，一共有几只？”引导学生根据图中信息，说前两句条件，再提一个数学问题。经过一段时间的训练，使学生有意识地从图中找已知信息，再根据已知信息提一个数学问题。通过这种句式的练习，无形中给学生一个信号，就是求未知量需要一些已知量。

图4

（2）“先条件，后问题”，规范主干模型。

如图1多数学生会根据习惯从左往右，从上往下读题。因此出现了“冰山后面有几只企鹅？右边有4只企鹅，一共有6只企鹅。”这样的表述顺序，与学生的思考顺序相背离，因此容易把问题解决成求总数。教师在教学过程中要充分关注学生的认知水平，引导他们按照“先条件，后问题”的顺序正确地进行表述。如：“一共有6只企鹅，右边有4只，冰山后面有几只？”这样的表述与学生的思考过程相吻合，他们也更容易找到解决问题的抓手。

3.建立条件或问题之间的联系。

当题目中情境复杂，数学信息比较多时，特别是有干扰信息出现时，部分学生就搞不清楚了。这时教师就要联系问题一步步引导学生舍弃不相干的信息。如图5要解决的问题是“还有几人没来”，而“我们队踢进了4个”这条信息与问题无关，当舍弃。再来读题就能清楚地得到解决问题的相关条件。

图5

二、培养符号意识，准确抽象

数学是一门抽象的学科，数学思想依赖数学符号进行演绎。数学符号化语言往往简洁清晰，便于读写运用。从一年级开始就要培养学生的符号意识，正确理解符号的含义，增强对符号的敏感性。

1.理解符号。

2.运用符号。

如图1这种“看图列式”的题，要培养学生用数学的眼光来看待问题，会用数学符号表示图意。如：用“6”表示总共的企鹅数，用“4”表示右边的企鹅数，“？”则表示左边的只数。经过分析，左边的只数是总数中去掉右边的只数，“去掉”要用“-”表示。

三、理解数量关系，准确建模

在小学数学教学中，要求学生能把实际的生活问题（原型）抽象成数学问题，再提出相应的数学表达式进行求解。如何提出正确的数学表达式呢？这就需要进行数量关系分析。“数量关系”是小学数学研究的重要内容。有效的关系分析，对建立模型思想起到关键的作用。

1.大小关系。

现实情境中比较物体的多少抽象成数学问题就是比较数量的大小。大小关系是最基本的数量关系。对于一年级学生而言，刚接触数量关系，需要用具体事物（原型）作支撑。

如图6，在教学中要先引导学生进行“一一对应”。两边个数相同，叫“同样多”，用“=”表示。建立“左边数量=右边数量”的模型；“一一对应”之后，左边还有个别多余，用“＞”表示，叫“左边数量＞右边数量”；“一一对应”之后，右边还有个别多余，用“＜”表示，叫“左边数量＜右边数量”。通过实物的比较，感知这种比较其实就是数量之间的比较，从而抽象出数量与数量的大小关系。建立大小关系模型，有助于后续等式和不等式相关知识的学习。

图6

2.加减关系。

（1）理解分与合的意义，感知数量关系。

学生从接触数学开始，就在不断地对复杂的现象进行抽象与概括。一年级“分合式”的内容，是后续加减法学习的基础。此外，通过分与合的学习，渗透分析与综合思想，抽象出基本的数学模型。

如图7，根据情境分向日葵。引导学生动手操作把4个小圆片分成两份，体验分的过程和分法的多样化。通过观察不同的分法，感受总数不变的情况下，一边数变大，另一边就要变小的函数思想。通过“分”建立起总数与部分数的关系：从总数里分出一部分后是另一部分；反之，把分开的两部分合起来就是总数。通过“合”，建立起部分数与总数的关系：这几部分之和与总数是相等的。借助各种感官促使学生建构“分”与“合”的认知。

图7

（2）理解运算意义，建立模型结构。

学生在解决问题时，要考虑情境问题与运算意义的联系。正确理解运算意义对有效分析数量关系起着至关重要的作用。因此，应加强运算意义的教学，创设情境，结合每一种运算逐步渗透每一种基本的数量关系，让学生充分经历思考和体验的过程以及探索运算意义的过程，帮助学生理解每个具体情境中的数量关系。

①认识“加法”运算的意义。

如图8，教师通过播放动画创设小丑变魔术情境，引导学生发现：小丑手上有3个红气球，一会儿又变了1个绿气球。求现在一共有几个气球？分析：要知道一共有几个气球，就得把红色和绿色两种气球合起来。合起来就要用加法，即：3+1=4。教师进一步引导：算式中“3”“1”和“4”分别表示什么？为什么用“+”？得出“求气球总数就是把红气球和绿气球合起来”。再探讨，红气球是总数的“一部分”，绿气球是总数的“另一部分”，合起来是“总数”。已知两个部分的数，求总数就是要把两个部分的数合起来，运用的就是加法运算。得出模型：一部分+另一部分=总数。

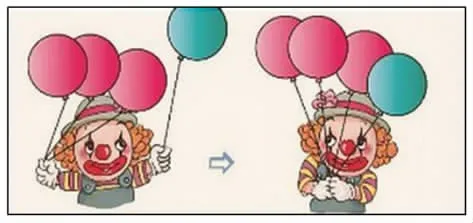
图8

②认识“减法”运算的意义。

如图9，教师通过播放动画创设小丑变魔术情境，引导学生发现：小丑手上有4个气球，飞走了1个绿气球。求现在还有几个气球？分析：要知道还有几个气球，就得从总数中去掉1个。去掉1个就表示减少了1个，即：4-1=3。教师进一步引导：算式中“4”“1”和“3”分别表示什么，为什么用“-”？得出“要求红气球，得从总数中去掉绿气球”。再探讨，红气球是总数的“一部分”，绿气球也是总数的“一部分”。已知总数和一个部分的数，求另一部分的数，就是要从总数减去已知部分，运用的就是减法运算。得出模型：总数-一部分=另一部分。

图9

（3）沟通分合式与运算意义，深度探讨模型关系。

分合式的学习是加减法运算教学的起点，在结合“解决问题”建立加减法模型后，再返回去与起点作沟通，对于学生理解模型能起到促进作用，在教学中是非常有必要的。我们以分式为例（如图10）：以习题为载体，有目的地将分合式与数量关系表达式进行联系，将新旧知识串联起来，深化学生对模型的理解。

图10

（4）运用多样化情境，充实数量关系模型。

创设多样化情境，为学生理解数量关系，顺利实现“化归”提供大量的原型支撑，多积累实例，以防情境定势。学生在积累、感悟了比较多的问题原型后，就能比较好地理解数量关系模型的使用范围。

加法：除了表示两个数合并外还可以表示增加、移入、接着数。

减法：除了表示求部分数外还可以作为减少、剩余、比较多少，往回数，加法逆运算等的模型。

如图10比较大小关系时，教师结合情境，帮助学生理解可以用减法运算比出它们的大小。从大数中减去与小数同样多的部分，多余部分就是大数比小数多的部分，也就是两数的相差部分，得出模型：“大数-小数=相差数”。

图11

在解决具体问题时，要沟通情境中的问题与数学意义的联系，潜移默化地渗透，让学生理解数量关系，顺利地实现对数量关系的理解和归纳，为学生解决问题能力的发展奠定基础。