面向创客教育的数学活动教学研究

吴华 翟凤琦

摘要：创客教育旨在开发、培养人的创造力。本文提出，面向创客教育的数学活动教学应以学生为中心，使学生经历问题呈现、活动准备、尝试操作、原型制作、整合反馈、归纳概括阶段，在各个阶段学生的各项能力都得到针对性锻炼，并以理解知识为基础整体提高学生数学创新能力。对于面向创客教育的数学活动教学实施，提升学生和教师素质是基础，营造良好的教学环境是重点，设计合理的数学活动是关键。

关键词：数学活动；数学活动教学；创客教育

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2018）13/14-0089-04

● 问题的提出

波利亚指出：“数学有两个侧面，一方面它是欧几里得式的严谨科学，从这个方面看数学像是一门系统的演绎科学；但另一方面，创造过程中的数学，看起来却像是一门試验性的归纳科学。”[1]在进行数学活动的过程中，学生可以在活动中通过试验得到相应的知识，通过创造活动归纳出相应的数学规律，数学活动教学是学生建构知识结构的有效学习方式。

随着高科技的迅猛发展、制造业的实力剧增，国际上创客运动兴起，“创客教育”应运而生，“创客教育”符合我国“创新教育”“素质教育”的理念，与数学活动教学有“异曲同工之妙”。因此，近年来我国学者开始对创客教育展开研究，研究方向有创客教育的内涵、创客教育与创新教育的关系、实施创客教育的可能途径、创客教育模型等。但是这些研究很少涉及创客教育与学科的结合、创客教育在教学中如何真正实施等问题。笔者针对现状，提出问题：如何开展面向创客教育的数学活动教学？

● 数学活动教学与创客教育

1.数学活动与数学活动教学

学生的数学活动主要是指学生在教师指导下开展的以实物，模型，数学的语言，数学的思想、方法和策略为操作工具，以完成某种教学任务为目标，通过看、听、说、做、思等形式，涉及认知、情感、意志、行动全面参与的学习数学和应用数学的行为活动、思维活动以及情感活动相互交织的活动集合体。[2]现在国际数学教育界比较一致的看法，认为数学教学是数学活动的教学，数学教学过程是数学活动的过程。[3]

2.创客教育

创客教育有三个核心要素，即制造/创造、创客空间和创客[4]，分别对应着传统教育中的学生活动、教学环境和学生。在创客教育中，学生的创造活动是要利用一定的工具、材料，借助一定的技术制造出某种物质产品；教育环境即创客空间给学生的创造活动提供了充足的设备和材料，也相应配备掌握综合知识的创客教师，可以将工程学、计算机科学、艺术等知识融合，给学生一定的指导；创客即学生，其不再通过单一的书本获取各科知识，而是在动手操作中发展综合素养，达到全面发展。

3.创客教育与数学活动教学

虽然随着科技的发展，越来越多的教师将信息技术应用于课堂教学，但信息技术的使用局限于动态呈现知识，并没有让学生亲身参与其中；同时，信息技术的使用只是帮助学生理解某一学科的知识，没有将各个学科相关知识联系起来。而在创客教育中，信息技术的优势得到凸显的同时，也将学科知识融合，如在数学中，以提升数学素养为“点”，提升综合素质为“面”。在面向创客教育的数学活动教学中，学生不仅进行思维的体操，更进行手指的体操，动手帮助头脑建构知识，提高自身参与度与知识的融合度。

● 创客教育下的数学活动教学阶段的构建

Allen和Yokana认为创客教师在培养创客学生时需经历四个阶段[5]：Getting Started、Experimenting、Prototyping、Integrating。笔者结合数学教学实际，将创客教育下的数学活动教学分为以下几个阶段（如图1）。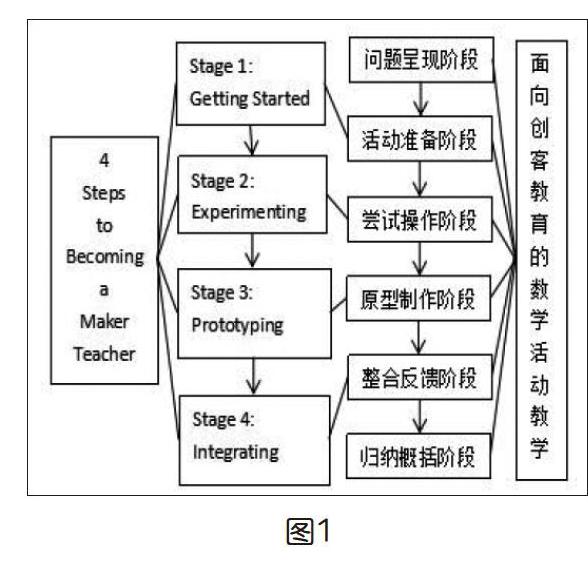

1.问题呈现阶段

建构主义学习观认为，只有建立在学生已有经验基础之上的问题情境才能帮助学生主动思考问题、理解问题，因此良好的问题是学生掌握知识的起点和关键。那什么样的问题是良好的问题呢？

首先，问题要具有情境性。问题应该是建立在学生经验基础之上的情境，这样学生才会体验到解决此问题的必要性，也有动力去解决这个问题。以实际情境为基础的问题要具有吸引力，这种吸引力的来源可以是不同于教材内容的问题提出方式、不同于常规的问题解决方式、不同于以往的问题解决结果等。

其次，问题要具有开放性。因教育背景、思维方式、知识储备等多重因素的影响，学生思考问题的角度各不相同，所以数学活动的设计不能局限学生的创造力，而应使学生的想象力、创造力有发展的空间，帮助学生在数学创造的过程中得到自我提升。

最后，问题要具有挑战性。对学生来说，没有比解决一个看起来有难度却被自己成功解决的问题更具有意义的事情，这可以增强学生的自我效能感，增强学生继续学习更高难度知识的欲望。但问题的挑战性要适度，问题不能太难也不能太容易。

教师在这个阶段要将问题的背景信息完整地传达给学生，并提出本节课要解决的数学问题，学生要尝试根据已有的知识基础分析问题，将旧知识迁移到本节课中。因此本阶段中教师的主导地位更加突出，学生知识迁移的能力和问题分析的能力得到提升。

2.活动准备阶段

在此阶段，学生开始对问题展开分析，包括解决此问题所涉及的概念、公式、定理等，也包括所涉及的数学思想、方法。教师在引导学生回忆旧知的过程中，潜移默化地影响学生的思考方向，同时要关注学生的进度，对没有思路、思路过“偏”的学生给予鼓励、支持、引导，对思路正确的学生给予肯定。

此阶段，学生的主体地位开始凸显，教师的主导地位逐渐弱化，教师更多的是以辅助者的身份参与到这个阶段的数学活动中。学生的搜集信息能力、综合信息能力得到发展。

3.尝试操作阶段

本阶段，学生对自己的方案进行初步尝试，这实际上是一个“试误”的过程。教师掌握班级内学生实验进度，适当引导学生朝下一阶段过渡。同时，教师要注意观察学生的情绪变化，要在语言、行动上调节学生情绪，培养学生控制情绪的能力。

4.原型制作阶段

原型制作阶段是面向创客教育的数学活动教学的核心部分，是学生真正在动手操作中理解、强化知识的过程。在这一过程中，教师可根据数学活动的类型和主题、实际教学需要，将学习水平相近的学生分为一组，每组完成不同难度的数学活动，也可以将不同学习水平的学生分为一组，每组完成相同难度但不同类别的数学活动。由于课堂时间有限，教师在巡查时要对学生的制作进度合理引导，帮助学生将抽象的设计具体化为产品，同时注重思维体操的过程。

这一阶段既考查了学生对知识的应用、拓展能力，也考查了其动手操作能力、创新能力，这是面向创客教育的数学活动教学与传统教育的最大不同之处。

5.整合反馈阶段

此阶段，要求学生演示本组的创客作品过程，就是對学生交流能力和表达能力的培养，同时，在教师的组织和引导下，各组学生对其他小组设计的创客作品进行评价，包括对设计思路、产品的实用性等方面的评价，在对其他作品进行评价的同时，也对自己作品反思，可以从他人的作品中吸取精华部分借鉴到自己产品中，用于产品设计的改进方案。

6.归纳概括阶段

教师在对学生制作的产品进行总结时，应引导学生对产品进行分类，从产品分类的角度引导学生对知识的分类进行讨论，进而概括产品类型，归纳分类特点，使学生头脑中散乱无章的知识点系统化，并将新的知识网络内化到学生头脑中的知识网络中，提高其归纳总结能力。

● 面向创客教育的数学活动教学的实施

实施面向创客教育的数学活动教学，以学生为中心，教师以四种角色身份进行引导，以数学活动为载体，以线下实体空间与线上虚拟空间为背景，以各方面支持为基石，构建实施模型（如图2）。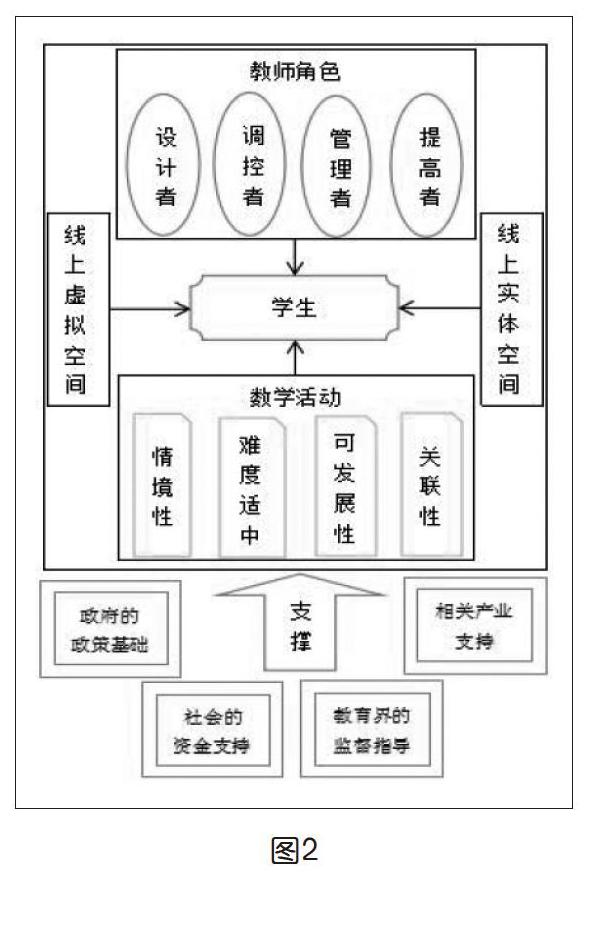

1.全面提升学生及教师能力是基础

创客教育下的数学活动教学在提高学生能力的同时，对教师也有了更高的要求。教师在教学中要具备以下几方面能力：①作为学习情境的设计者，教师要具有融合其他学科知识的能力、结合实际问题设计开发学生在数学活动中创造力的能力；②作为人员资源的管理者，教师要合理分配学生的交流协作，考虑学生性格特点、知识水平、学习兴趣等因素，同时对现有的资源如设备、工具等进行合理分配；③作为学生学习的调控者，教师要跟踪学生制作进程，为学生搭建适当的支架；④作为实践质量的提高者，教师要为学生提供技术、工具的使用等方面适时、适量的帮助等。

2.营造良好的教学环境是重点

出于实际教学需要，在以数学活动教学为目的的创客空间（以下简称数学创客空间）中主要配备简单易操作的设备、与数学专业相关的软件等。

数学创客空间应包括线下的实体创客空间，也包括线上的虚拟创客社区。实体创客空间可以分为校内数学创客空间和校外（社会）数学创客空间，二者相互衔接，互为补充：校内创客空间由教师指导，更侧重各个学科知识的融合，但以凸显数学学科知识为主，强化学校数学教育效果，提高学生对数学知识的理解能力和创造力，校外创客空间可以聘请某一领域的专业人士进行指导，更侧重数学知识在该领域的实践与应用，有助于学生的个性化发展，所制作的数学创客产品也可被相关企业改良进而投入生产。学生可以在实体创客空间中制作数学创客产品，在虚拟创客社区进行展示交流，交流制作心得，分享制作过程涉及的软件平台和工具、所利用的相关数学知识，也可以在虚拟创客社区中浏览自己感兴趣的其他数学创客产品，从他人的产品借鉴中得到启发。

3.设计合理的数学活动是关键

结合数学学科特点和实际教学需要，在数学活动中的创客课题应具有以下基本特点。

①情境性。数学问题来源于实际生活，数学服务于实际生活，教师所设计的数学活动必须与实际生活相关，才能让学生有解决问题的动力，进而获得成就感。

②难度适中。数学活动的设计初衷是为数学教学服务，在实际教学中，难度太大的数学活动会消耗大量时间，致使教学进程被延误，不能按时完成教学任务，难度太小的数学活动不能使学生在活动中获得知识后得到自我成就感，丧失对数学活动的兴趣，不利于后续数学活动的展开。

③可发展性。针对同样一个主题的数学活动，学生创造出的创客产品应是各具特色的，也就是说，数学活动的设计不能使学生的创造力受限，而应使学生的想象力、创造力有发展的空间，使学生在创造的过程中得到自我提升；在探索创客课题时，教师不需要对探索的方向、深度、广度做出明确的规定，学生可以依据自己的兴趣、实力等主观因素投入精力到课题的研究上。

④关联性。这里强调关联性要“适度”是因为，创客教育在多个学科领域综合发展人的创新能力，势必要求学生掌握多方面综合知识，但由于各自的教育背景、学习基础不同，每个学生在各个领域对知识的掌握情况也不尽相同，因此数学活动本身不能与某一方面知识具有过深的联系，但在进行数学活动时，可以让对某方面知识掌握较好的学生发挥自身长处进行创造活动，以达到对各层次水平学生的兼顾。

● 结语

创客教育对于我国来说是“舶来品”，创客教育在中国化的过程中难免会遇到问题，如如何将传统课程与创客教育融合、如何培养创客教师、如何评价创客教育效果等，但创客教育也为我国的素质教育、创新教育提供了新的思路。高等院校和各级教育研究所的研究者应和中小学教师密切配合，将理论与实践相结合，寻找适合我国的创客教育模式，培养出符合国家发展需要的创新型人才。

参考文献：

[1]G·波利亚.怎样解题[M].阎育苏，译.北京：科学出版社，1982.

[2]仲秀英.学生数学活动经验研究[D].重庆：西南大学，2008.

[3]涂荣豹.数学教学认识论[M].南京：南京师范大学出版社，2003.

[4]Halverson，E.R.&Sheridan;，K.M.The Maker Movement in Education[J].Harvard Educational Review，2014，84（4）：495-504.

[5]Allen G.，Yokana L.4 Steps to Becoming a Maker Teacher[EB/OL].http// gettingsmart.com/4-steps-becoming-maker-teacher/2018-01-01.

作者简介：吴华，辽宁师范大学教师教育研究中心、数学学院教授，硕士生导师；翟凤琦，辽宁师范大学数学学院硕士研究生。

基金项目：辽宁省高等教育学会“十三五”规划高教研究课题“互联网背景下整合技术与大学课堂教学的理论与实践研究”（项目编号：GHYB160077）；辽宁省教育科学“十三五”规划2017年度课题“互联网下整合技术与基础学科教学的研究与实践——以辽宁省数学学科为例”（项目编号：JG17CB360）。