经编机梳栉横移系统误差建模与仿真

苏柳元， 孟 婥， 张玉井， 赵义满

(东华大学 机械工程学院， 上海 201620)

梳栉横移系统是现代高速经编机的关键组成部分，经编花型是在成圈机构和梳栉横移系统有规律的配合下形成的。梳栉的横移运动速度高，且启停频繁，梳栉横移运动的位移误差会引起擦针等现象，阻碍经编机的高速化发展[1-2]。

近年来，许多研究人员对梳栉横移系统横移误差的影响因素进行了研究：夏风林等[1]指出控制系统和机械结构是影响梳栉横移系统横移误差的 2个主要原因，但并没有详细分析机械结构是如何对横移误差造成影响的；文献[2-4]分别基于前馈控制、速度控制和矩阵控制模式设计了梳栉横移控制系统，以保证导纱梳栉的精确定位，但也没有从机械结构的方面进行研究；刘念等[5]基于牛顿运动定律建立了梳栉横移系统的动力学模型，并通过实验进行验证，但这个模型比较简单，没有考虑到梳栉横移系统的复杂支承形式和细长件柔性。

一些学者还基于赫兹(Hertz)接触理论和有限元法对丝杠进给系统、连杆机构和加工中心的动态特性进行了研究[6-8]：Wang 等[9]基于Hertz接触理论和连续接触模型研究了丝杠进给系统的动态特性；Megahed等[10]基于Hertz接触理论研究了转动副间隙对机械系统动力学特性的影响；蒋书运等[11]基于Hertz理论和有限元法建立了立式加工中心的动力学模型。这些研究均为经编机梳栉横移系统误差的研究提供了参考，但利用Hertz接触理论对直线滚动轴承和滚珠导套的径向刚度进行分析，对复杂支承运动系统的动力学特性进行研究的论文还相对较少。本文同时考虑了梳栉横移系统滚动结合部刚度，以及导纱梳栉、球铰和异形连接件等细长件的柔性，通过ANSYS和ADAMS进行刚柔耦合分析，建立其横移误差模型，并基于现有的加固架驱动和重心驱动2种梳栉横移系统，分别研究导纱梳栉的质量和刚度对横移误差的影响，提出有效减少横移误差的措施。

1 滚动结合部的动力学特性

1.1 梳栉横移系统的动力学模型

本文以国产某高速经编机梳栉横移系统为原型，其结构简图如图1所示。

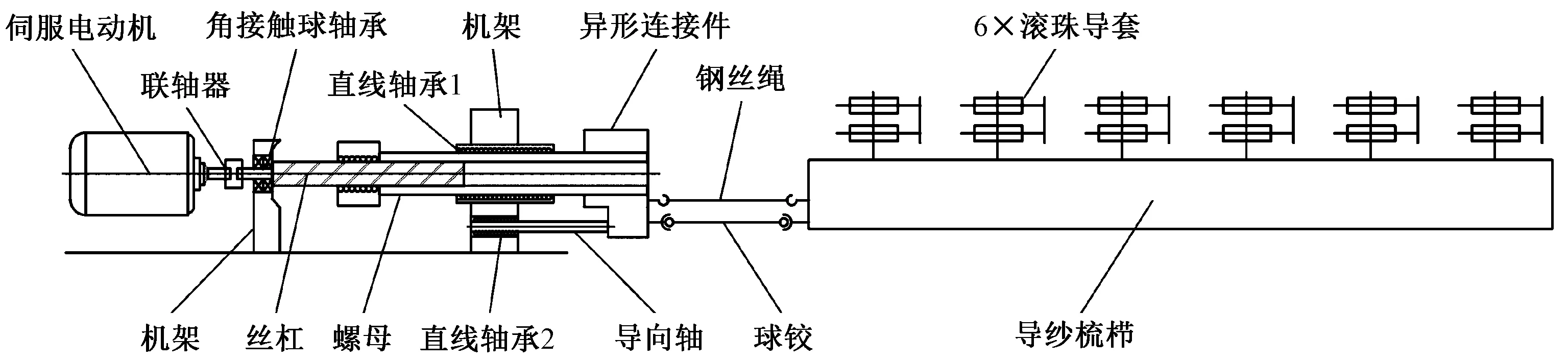
图1 梳栉横移系统结构简图Fig.1 Structural diagram of guide bar shogging system

从图1可以看出，梳栉横移系统由伺服电动机、滚珠丝杠副、球铰、钢丝绳、导纱梳栉和导向元器件构成。伺服电动机驱动滚珠丝杠，通过球铰将导纱梳栉推出，再通过钢丝绳拉回。伺服电动机与滚珠丝杠通过无间隙刚性联轴器连接，有效避免了由联轴器的间隙和弹性变形引起的输出运动误差。滚珠丝杠副为特殊定制，由于螺母外伸需要对丝杠螺母副采用特殊的支撑方式：一端由角接触球轴承支承在丝杠上，另一端由直线轴承1支承在长螺母上，并通过导向轴和直线轴承2进行导向。由于导纱梳栉跨距过长，需采用6对滚珠导套进行支承和导向。

梳栉横移系统机械结构对其横移误差的主要影响因素可总结为2点：1)滚动结合部的刚度特性。由于丝杠支承方式特殊，系统支承形式多样，支承数目较多，角接触球轴承、滚珠丝杠副、直线轴承和滚珠导套等滚动结合部的动态特性是产生横移误差的关键因素；2)细长零部件的柔性。在横移系统中，球铰、梳栉等零部件，由于自身长度较长、截面较小，易产生柔性变形导致横移误差。球铰与丝杠螺母不同轴，异形连接件在偏转力矩作用下也会发生弯曲变形。

1.2 滚动结合部刚度计算

Hertz 接触理论是计算弹性体接触变形和接触应力的经典理论[12]。图2示出Hertz接触理论中常见的任意两曲率物体的接触状态。在外力P的作用下，物体V1和V2相互挤压接触，两物体满足以下假设条件[13]：相互接触两物体的材料是均匀且各向同性的；接触表面光滑，只存在法向作用力，不存在切向摩擦力；接触物体只发生弹性变形，并服从胡克定律；接触面的尺寸和接触物体表面的曲率半径相比是很小的。

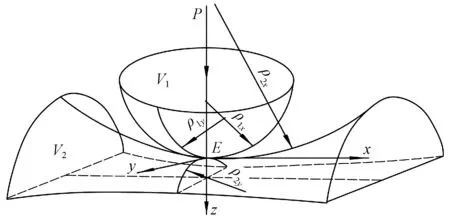
图2 Hertz接触理论示意图Fig.2 Schematic diagram for Hertz contact theory

在接触区域中心，两物体沿z轴方向由于压缩变形引起的相对位移量δ(m)为

(1)

J和na可通过计算下式在文献[13]中查得。

τ=

式中：u1、u2为两接触体的泊松比；E1、E2为两接触体的弹性模量，Gpa；φ0为两接触体主平面之间的夹角，(°)；P为法向作用力，N；∑ρ为两接触弹性体在接触点处的综合曲率(m-1)，即

式中：ρix表示接触体i在xz平面的曲率，m-1，ρiy表示接触体i在yz平面的曲率，m-1；i=1,2。

1.2.1滚珠丝杠结合部刚度

滚珠丝杠副由丝杠、滚珠和螺母组成，滚珠与丝杠和螺母滚道的接触满足 Hertz 接触理论的 4 个条件[14]。梳栉横移系统滚珠丝杠副采用错位预压的方式进行预紧，忽略工作时外部轴向载荷的影响，预紧力Fa(N)作用下滚珠丝杠结合部的受力分析如图3所示。

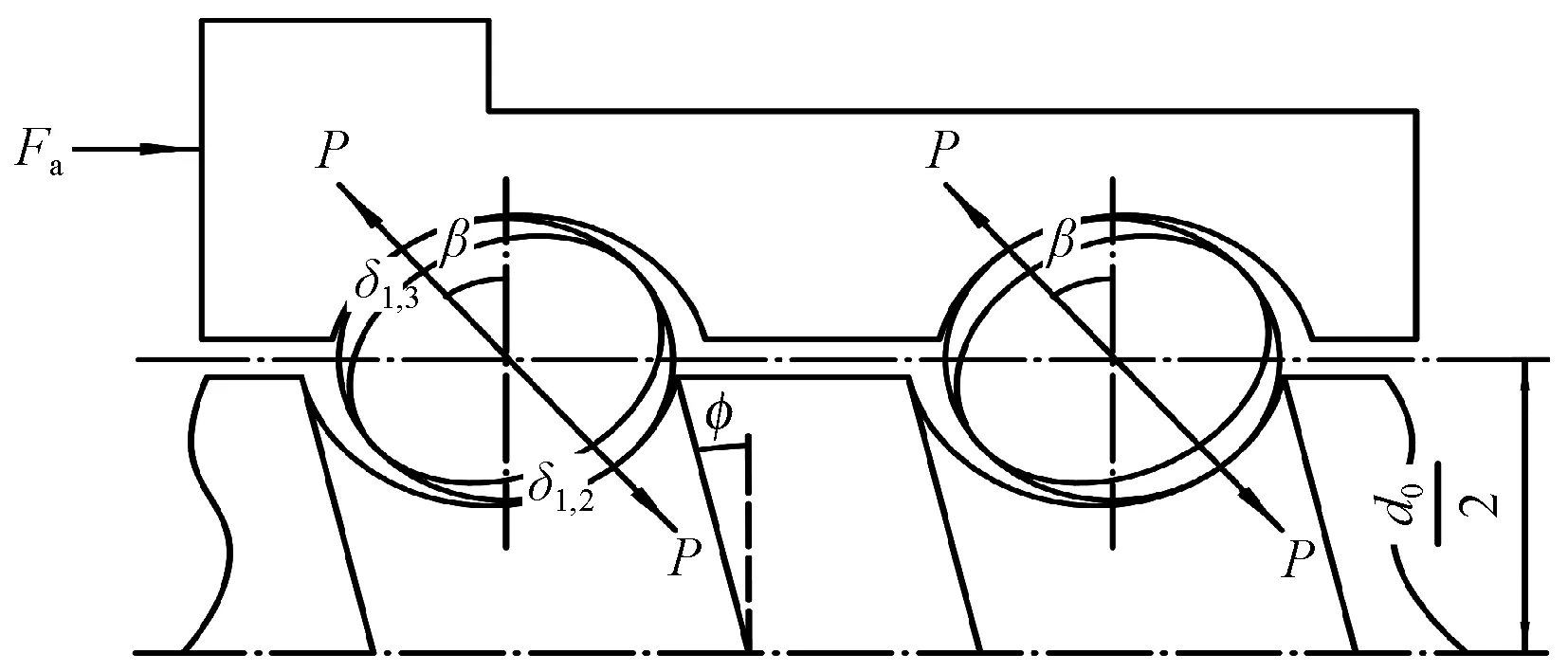
图3 滚珠丝杠结合部受力图Fig.3 Force diagram of ball screw

滚珠与滚道接触的压力角为β(°)，将滚珠、丝杠、螺母分别标记为1、2、3，则滚珠与丝杠滚道和螺母滚道的接触变形分别为δ1,2和δ1,3，滚珠与丝杠滚道和螺母滚道的密合度为f1,2和f1,3，滚珠数目为Z。

由螺母在轴向受力平衡可得:

Fa=PZsinβcosφ

(2)

(3)

式中：d0为丝杠公称直径，mm；db为单个滚珠直径，m；φ为丝杠螺旋升角，(°)；综合曲率∑ρ1,i=ρ1x+ρ1y+ρix+ρiy，m-1，i=2,3。接触变形

(4)

i=2,3

(5)

由几何关系可得，螺母与丝杠滚道面间的法向弹性位移Fa(m)，在轴线方向上将引起螺母相对于丝杠的轴向弹性位移：

(6)

即

轴向刚度

(7)

滚珠丝杠副的基本参数和结合部刚度如表1所示。

表1 滚珠丝杠副基本参数和结合部刚度Tab.1 Basic parameters and stiffness of ball screw

1.2.2角接触球轴承轴向和径向刚度

固定端成对使用角接触球轴承，采用轴向定位预紧的方式，预紧时轴承内、外环只产生轴向相对位移，预紧后受外载荷作用，轴承间距保持不变。轴承结合部受力分析如图4所示。

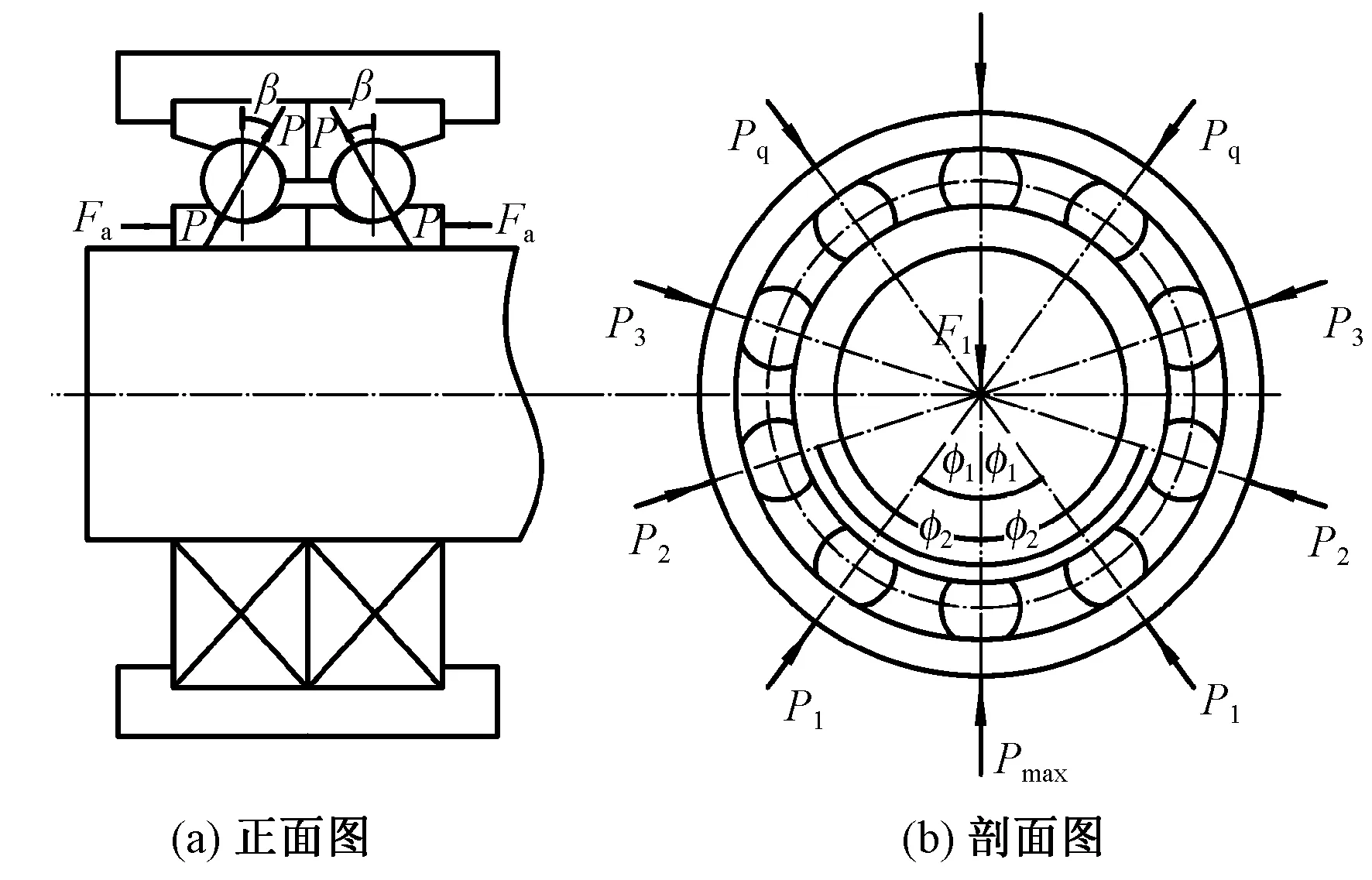
图4 角接触球轴承结合部受力图Fig.4 Force diagram of angular contact ball bearing.(a)Front view；(b)Cross-section

丝杠工作时对轴承的轴向和径向作用力较小，可忽略不计，将滚珠、轴承内圈滚道、轴承外圈滚道分别标记为4、5、6，则滚珠与轴承内圈滚道、轴承外圈滚道的接触变形分别为δ4,5和δ4,6，滚珠与轴承内圈滚道和轴承外圈滚道为f4,5和f4,6。根据单个轴承轴向受力平衡可得

Fa=PZsinβ

(8)

式中，β为接触压力角，(°)。

根据几何关系得到接触点处的4个主曲率

(9)

在接触点处的综合主曲率

∑ρ4,i=ρ4x+ρ4y+ρix+ρiy,i=5,6

(10)

接触变形量

(11)

令

假设仅受径向外载荷作用时，轴承内外圈仅有相对径向位移而无轴向位移。轴承轴向预紧后，受到径向载荷Fr作用，各滚珠处的弹性变形

δq=δasinβ+δrcosβcosφq

(12)

式中，φq为第q个滚动体中心与最大负荷滚动体中心之间的夹角，(°)。第q个滚珠的负荷为

(13)

可得轴承的轴向载荷Fa=Pqsinβ

(14)

轴承的轴向刚度Ka(N/m)由式(15)计算可得

(δasinβ+δrcosβcosφq)1/2

(15)

轴承的径向载荷为：

Fr=∑Pqcosβcosφq=

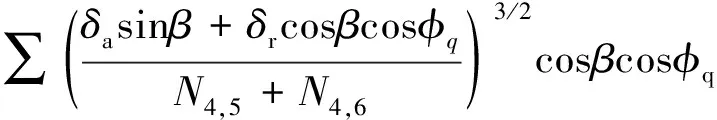
(16)

轴承在主轴工作中，δr较小而δa较大，可认为Fr与δr为线性关系， 径向刚度为常数。δr=0时轴向刚度值(N/m)为

(17)

轴承的径向刚度kr(N/m)为

δrcosβcosφq)1/2(cosφq)2

(18)

(19)

角接触球轴承的基本参数和结合部刚度如表2所示。

表2 角接触球轴承基本参数和结合部刚度Tab.2 Basic parameters and stiffness of angular contact ball bearing

1.2.3直线轴承径向刚度

直线轴承结合部受力如图5所示。直线轴承在径向力作用下轴心和外圈在外力方向上发生相对位移δr(m)。根据变形协调方程，第q个滚动体的弹性变形量δq=δrcosφq，其中φq为第q个滚动体位置角(径向负荷作用位置为0位置)，滚动体总个数为K。

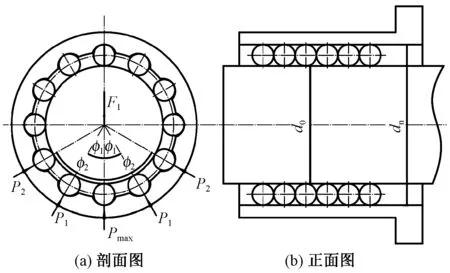
图5 直线轴承结合部受力图Fig.5 Force diagram of linear bearing.(a)Cross-section；(b)Front view

将滚珠、轴承外圈和导向轴分别标记为7、8和9，根据负荷与变形的关系，得到

(20)

径向力的平衡方程表示为：

(21)

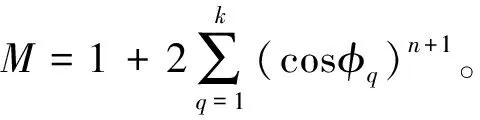
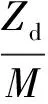
(22)

式中：Zd为一周滚珠列数；nd为每列承载滚珠数目。

(23)

(24)

(25)

(26)

直线轴承1和2的基本参数和结合部刚度分别如表3、4所示。

1.2.4滚珠导套径向刚度计算

滚珠导套结合部受力图如图6所示。滚珠导套的径向刚度计算与直线轴承类似，只是由于结构的差别，主曲率的计算方式不同，将滚珠、轴承外圈、轴分别标记为9、10、11，主曲率如式(27)所示。

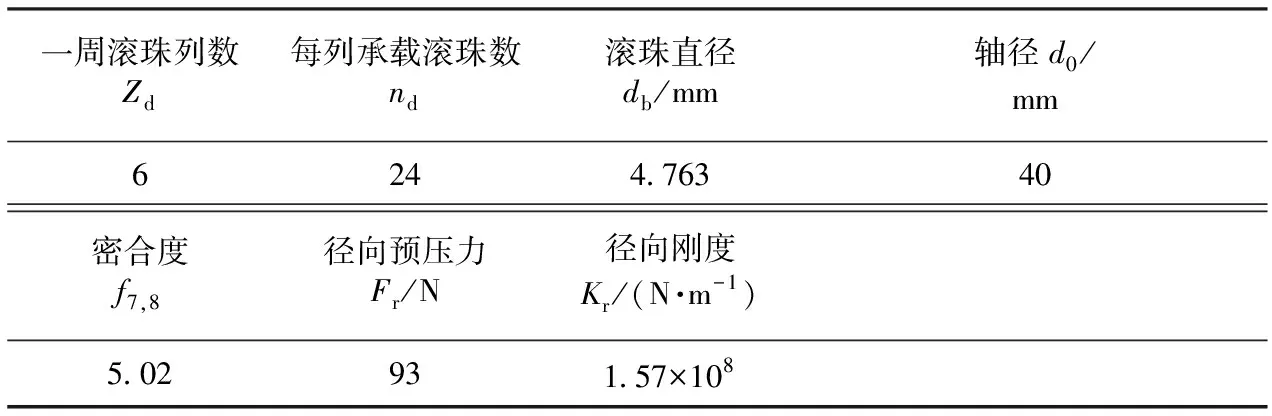
表3 直线轴承1基本参数和结合部刚度Tab.3 Basic parameters and stiffness of linear bearing 1

表4 直线轴承2基本参数和结合部刚度

(27)

图6 滚珠导套结合部受力图Fig.6 Force diagram of guide bushing.(a)Cross-section；(b)Front view

其他计算步骤与直线轴承类似，滚珠导套的基本参数和结合部刚度如表5所示。

表5 滚珠导套基本参数和结合部刚度Tab.5 Basic parameters and stiffness of guide bushing

2 刚柔耦合动力学模型的建立

本文通过Solidworks建立梳栉横移系统的机械结构模型，将梳栉、球铰和异形连接件等细长件导入ANSYS生成模态中性文件，通过ANSYS 和 ADAMS 联合仿真建立梳栉横移系统的刚柔耦合动力学模型，如图7所示。

图7 刚柔耦合动力学模型Fig.7 Rigid-flexible coupled dynamic model

输入预定的运动规律进行仿真，仿真参数确定步骤如下。

1)目前，横移梳栉的材料一般为镁铝合金、碳纤维复合材料和铝合金3种，材料属性如表6所示。球铰为Q235材料，异形连接件为铝合金材料。

表6 梳栉材料属性Tab.6 Guide bar material attributes

2)根据Hertz接触理论计算出梳栉横移系统滚动结合部的刚度特性，如表7所示。

表7 滚动结合部刚度Tab.7 Stiffness of mechanical joints

3)考虑转速n=1 000 r/min，针背横移角为120°，针背停歇角为90°，针前横移角为60°，针前停歇角为90°[15]。

4)机号E24，则针距l=1.058 3 mm，驱动采用针前横移1针距，针背横移3针距的运动方式，用step函数得到理想位移曲线，逆求得到理想驱动角速度曲线。在刚柔耦合模型6个直线轴承的正下方导纱针尖处取6个Marker点，仿真得到这6个Marker点的位移曲线，与理想位移曲线相减即为这6个marker点处的横移误差曲线。仿真结果表明，最靠近球铰连接的marker点处横移误差最大，后文所述横移误差皆为该点处的横移误差。

3 质量和刚度对系统横移误差的影响

现有的电子梳栉横移系统主要有2种驱动方式：加固架驱动和重心驱动，如图8所示。在加固架驱动横移系统中，L型固架同时作用在梳栉左端和梳栉左端安装的2个直线轴承导套中部，可减小偏转力矩以及偏转力矩作用下滚珠导套的倾斜和梳栉的弯曲变形。重心驱动方式则可克服横移过程中由于附加力矩产生的偏振现象，使运动更为平稳[16]。本文基于这2种梳栉横移系统，分别研究导纱梳栉的质量和刚度对横移误差的影响。

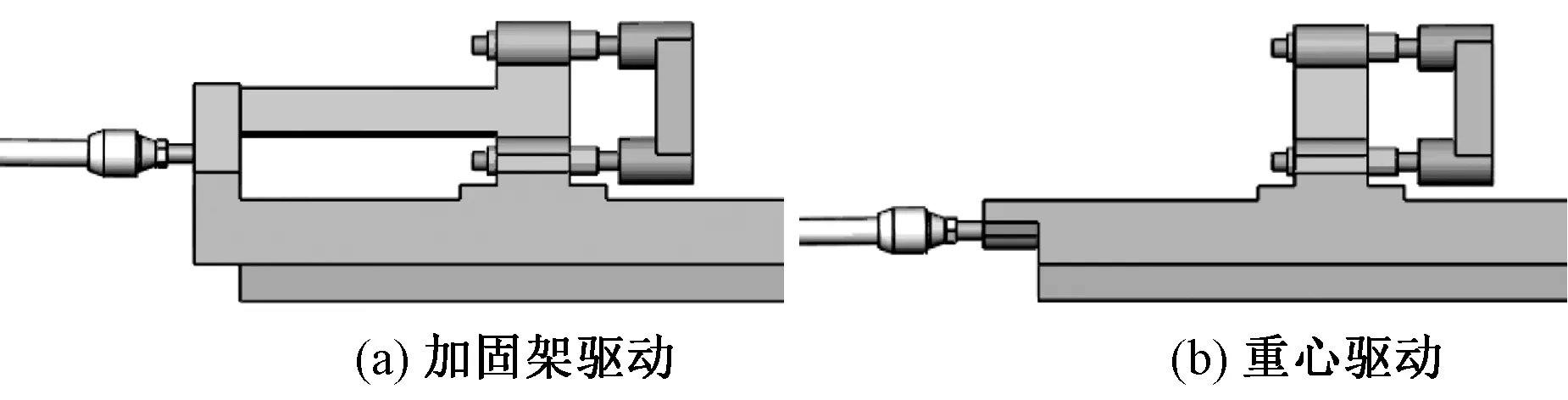
图8 2种梳栉横移系统驱动方式Fig.8 Two drive modes of guide bar shogging system.(a)Frame drive；(b)Center of gravity driven

根据表6，在材料属性范围内梯度改变梳栉材料的密度和弹性模量，以研究梳栉的质量和刚度对系统横移误差的影响。等差设置梳栉材料密度为 1 800、2 000、2 200、2 400、2 600、2 800 kg/m3共 6组进行仿真，得到横移误差曲线如图9所示。可以看出，随着梳栉质量增加，2种系统的横移误差均明显增大，因此，可在保证梳栉刚度不变的情况下，改变梳栉的结构和材料减轻梳栉质量，以达到减小系统横移误差的目的。就经编横移工艺要求而言，横移系统的精度要求一般在0.03 mm以内。图中还显示，当梳栉密度在1 800～ 2 800 kg/m3范围内变化时，重心驱动横移系统的横移误差均可以满足设计要求，而使用加固架驱动方式时，需保证梳栉密度小于2 000 kg/m3。

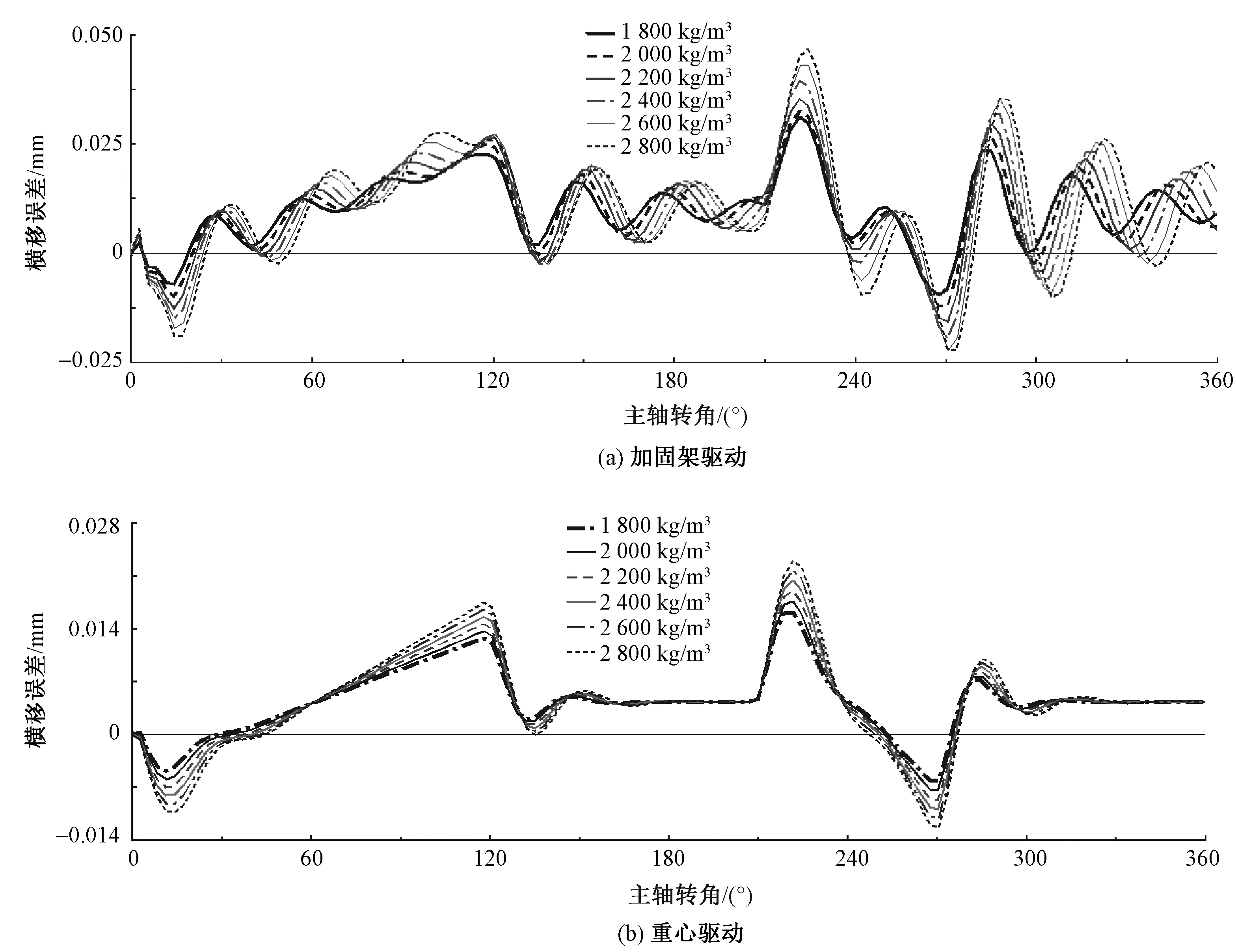
图9 不同质量梳栉的横移误差曲线Fig.9 Transverse motion error with different density. (a)Frame drive；(b)Center of gravity driven

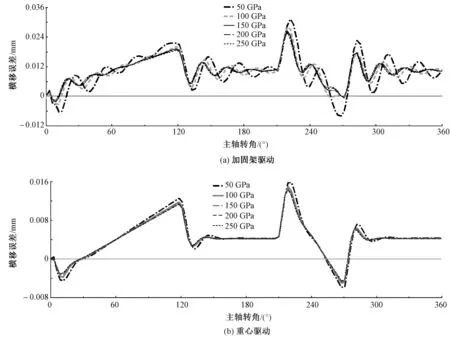
图10 不同刚度梳栉的横移误差曲线Fig.10 Transverse motion error with different elasticity modulus.(a)Frame drive；(b)Center of gravity driven

等差设置梳栉材料的弹性模量为50、100、150、200、250 GPa共5组进行仿真，得到横移误差曲线如图10所示。

由图10可以看出，随着梳栉刚度增加，2种系统的横移误差均减小，但对于重心驱动横移系统，梳栉的刚度变化对横移误差的影响不明显。这是由于系统的横移误差主要由梳栉和异形连接件在偏转力矩下的弯曲变形以及梳栉和球铰在轴向推力下的压缩变形产生，当梳栉质量增加时，轴向惯性力增大，梳栉和球铰的压缩变形增大，因此，2种驱动方式的横移误差均增大；当梳栉刚度增加时，梳栉在偏转力矩下的弯曲变形和轴向推力下的压缩变形均减小，而重心驱动方式可有效克服梳栉在横移过程中产生的偏转力矩，从而减小了对梳栉刚度的要求。仿真结果表明，重心驱动方式在减少梳栉横移误差方面具有优越性。

4 结 论

1)在高速经编机的梳栉横移系统中，滚动结合部的动态特性以及梳栉、球铰和异形连接件等细长件的柔性，导致系统实际横移位移与理想横移位移存在误差，这种横移误差会引起擦针现象，阻碍经编机的高速化发展。

2)利用Hertz接触理论计算梳栉横移系统滚动结合部的刚度特性，并用ANSYS软件与ADAMS软件进行刚柔耦合仿真，可很好地模拟梳栉横移运动过程，得到系统梳栉横移误差。

3)系统的横移误差主要由梳栉和异形连接件在偏转力矩下的弯曲变形以及梳栉和球铰在轴向推力下的压缩变形产生：当梳栉质量增加时，轴向惯性力增大，梳栉压缩变形增大，导致横移误差增大；当梳栉刚度增加时，梳栉在偏转力矩下的弯曲变形和轴向推力下的压缩变形均减小，而重心驱动方式可有效克服横移过程中产生的偏转力矩，从而减小了对梳栉刚度的要求。仿真结果表明，重心驱动方式在减少梳栉横移误差方面具有优越性。