应用图像处理的纱线黑板毛羽量检测与评价

陆奕辰， 王 蕾， 唐千惠， 潘如如， 高卫东

(生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

纱线毛羽不仅影响纱线中纤维的有效利用率与强度，还影响织物的透气和外观性能等，是反映纱线质量的重要指标之一[1]。纱线毛羽检测的常用方法有人工目测法和光电法：采用人工目测法观察毛羽，取样数量少，测试效率低，且结果易受人为因素影响；UT5型乌斯特仪上的毛羽测试模块是最常用的利用光电法测量毛羽的设备，其输出结果可对照乌斯特统计公报找出纱线的毛羽水平，但很多中小规模的纺纱厂或印染厂常因乌斯特仪设备价格昂贵或实验条件限制等问题，无法使用其进行毛羽检测。

运用图像处理技术检测纱线毛羽量已成为纱线外观测量的趋势：OZKAVA等[2]通过区分背光图像和暗场图像，提出采用图像直方图确定背光图像的2个阈值，分别表示纱线条干和毛羽，但此法不适用于具有相近阈值的纱线条干和纱线毛羽图像的检测；张继蕾[3]结合图像处理和多区域轮廓跟踪算法完成纱线毛羽的自动检测；Fabijanska等[4]先后采用中值滤波和高通滤波对纱线图像进行预处理和阈值分割，然后基于Canny边界检测提取纱线毛羽；孙银银等[5]经灰度变换、图像分割、图像细化处理等，得到较完整的纱线条干和毛羽图像，以纱线条干边缘为基准线，判断毛羽分割点，得到不同长度的毛羽根数；Wang等[6]利用双平面镜成像原理开发了一套纱线三维重构算法，通过纱线多个角度所呈的像重建纱线的三维模型，进而得到毛羽的实际长度。上述研究中，均采用纱线图像减去纱线条干的算法得到毛羽图像。若能直接获取毛羽信息，则可简化图像处理程序，提高检测效率。此外，这类研究方法得到的毛羽信息，如毛羽长度和根数，虽较准确但无法给出图像毛羽整体水平的检测结果。

根据上述现存问题，本文首先提出一种基于图像处理技术的纱线黑板毛羽量检测方法，即采用扫描仪获取均匀绕在黑板上的纱线灰度图像，对图像进行中值滤波、二值化处理和纱线形态学运算后，分割得到纱线条干和膨胀过的纱线条干，再通过局部阈值分割法，提取图像中的毛羽信息，进而统计整张图片的毛羽像素个数。根据图像处理的结果，提出毛羽量指标M指数，并比较了M指数与乌斯特仪测得的毛羽值(H值)，得到二者的关系式。

1 纱线图像采集

1.1 实验仪器与材料

仪器：VHX-5000型数码显微系统，基恩士(中国)有限公司；9000F Mark2型扫描仪，Canon公司；YG381型摇黑板机，南通宏大实验仪器有限公司；UT5型乌斯特仪，乌斯特技术有限公司。

材料：原料、线密度和纺纱方式各不相同的纱线共计18种，试样1#～9#产自杭州日南纺织有限公司，试样10#～18#产自常州立万纺织品有限公司。其具体参数如表1所示。用于模型验证的纱线共 6种，产自杭州日南纺织有限公司，编号为19#～24#。

1.2 图像采集参数

图1示出纱线在不同状态下的图像。图1(a)为用基恩士VHX-5000拍摄的自然状态下纱线图像，图1(b)为同一镜头下、用载玻片盖住同片段纱线，以模拟扫描仪状态下的毛羽。通过对比可发现：图1(a)圆形框内的试样由于毛羽处于悬浮状态而导致失焦，且与条干部分重合的毛羽也无法显示；图1(b)中经载玻片压平后，原本不在一个平面内的毛羽显示了出来，毛羽信息较图1(a)更清晰、全面，因此，使用扫描仪可将二维纱线图像上与条干不在同一焦平面上的毛羽通过压平的方式显示出来，可减小实验误差，提高图像处理结果的可靠度。

表1 试样参数

图1 纱线在不同状态下的图像Fig.1 Image of yarn in different states.(a)Natural state；(b)Covered state by glass slide

不同于CCD工业相机和视频显微镜，扫描仪可自定义采集分辨率。当扫描分辨率为800像素时，纱线毛羽与黑板背景的分界不清晰，部分毛羽模糊，不利于准确计算纱线毛羽量；当分辨率大于 2 000像素时，实验准确性大大提高，但分辨率越高、存储空间越大，处理速度就越慢。为兼顾纱线毛羽的清晰度和图像处理速度，实验中选用1 200像素扫描分辨率，扫描介质为黑白型，即纱线图片为灰度图像，可直接减少图像处理的计算量，便于后续的纱线图像处理。

依次将18种试样利用YG381型摇黑板机均匀缠绕在220 mm × 250 mm的黑板上。通过9000F Mark2扫描仪获取纱线黑板图像并将采集的图像输入计算机。为减小误差，将黑板边缘的纱线排除在测量范围之外，实验时每张图片截取图像大小为 9 000 像素 × 10 800 像素，实际对应83根纱线，总长为18.97 m，黑板区域为190.5 mm × 228.6 mm。图2示出11#号试样(即线密度为9.83 tex的紧密赛络纺涤纶纱线)的局部采集图像。

图2 黑板纱线局部采集图像Fig.2 Local collection image of blackboard yarn

2 图像处理

以11#试样为例，阐述本文提出的用图像处理计算纱线黑板毛羽量的方法。实验过程中，首先对试样图像进行预处理，然后采用形态学运算处理纱线条干部分，最后获得纱线毛羽量。

2.1 图像预处理

为消除黑板上遗留的粉尘干扰，采用medfilt函数先对纱线黑板图像进行中值滤波。中值滤波在衰减噪声的同时不会使图像的边界模糊。选用的滤波窗口为3像素× 3像素。

然后，将纱线灰度图像转换成二值图像。使用最大类间方差法找到图像的全局最优阈值，该阈值为[0,1]内归一化的强度值。当目标与背景的分割阈值为t时，目标像素点占整个图像比例为w0，平均灰度为μ0；背景像素点占整个图像比例为w1，平均灰度为μ1。整个图像平均灰度为

μ=w0μ0+w1μ1

(1)

此时，该图像的类间方差为

g(t)=w0(μ0-μ)2+w1(μ1-μ)2

(2)

当g(t)取得全局最大值时，所对应的t为最佳阈值。

设原灰度图像为f(x,y)，二值化后的图像为g(x,y)。二值化的过程[7]如下：

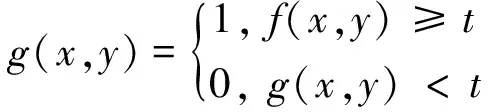
(3)

图3为11#试样上某段纱线图像预处理前后的对比图。由于毛羽本身柔软，以致光照不匀造成纱线图像中同根毛羽上不同部位出现灰度不匀的情况，因此，导致图3(b)预处理图像遗失部分毛羽信息，这也是本文提出的新算法旨在解决的问题。

图3 纱线图像预处理前后对比图Fig.3 Comparison of original(a)and preprocessing (b) image of yarn

2.2 形态学运算

本节采用形态学运算对纱线二值图像进行运算，得到纱线条干图像。图像形态学运算的原理是利用结构元素B对图像A作开运算，记为A°B[8]，其定义为

A°B=(AΘB)⊕B

(4)

式中，(AΘB)⊕B表示A先被B腐蚀，然后被圆盘型结构元素B膨胀。

图4示出用不同半径r的圆盘结构元素对图3(b)进行形态学运算的结果。当圆盘结构元素B的半径为1或2像素(文中半径r的单位为像素的点个数，以下单位省略)时，纱线条干图像上有些毛羽像素未被处理(见图4(a)的Ⅰ区域和4(b)的Ⅱ区域)；当圆盘结构元素为5时，图像被过度腐蚀，造成条干部分中断(见图4(d)的Ⅲ区域)，所以半径r为1、2或5的圆盘结构元素B均不适用于纱线的形态学开运算。图4(c)显示，当圆盘结构元素B的半径r为3时，形态学开运算使纱线较完整地保持了纱线条干特征，同时消除了毛羽和背景点，运算结果较好。

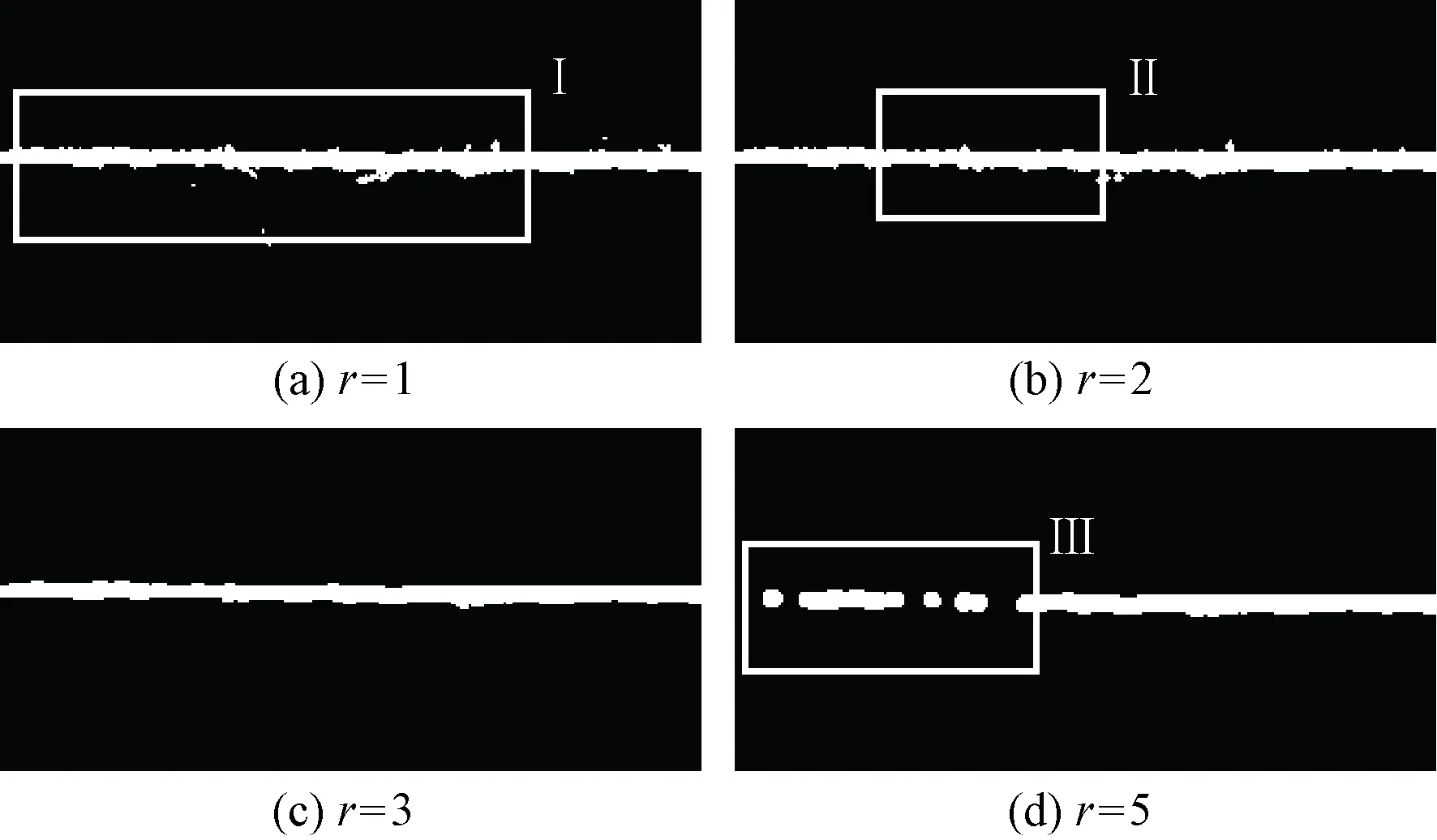
图4 不同圆盘半径时的形态学开运算图像Fig.4 Image of morphological open operation with different disk radius

为得到完全去除条干并只有毛羽的图像，还需对纱线条干作膨胀处理。图像膨胀的原理是利用结构元素D对图像C进行膨胀，记为C⊕D，定义为

C⊕D=[CEΘ(-D)]E

(5)

式中，D为圆盘型结构元素。

图5示出不同圆盘半径时的膨胀处理图像。当结构元素D的半径r取0，即图像未作膨胀处理时(见图5(a))，或结构元素D的半径r为3(见图5(b))时，图像上均会遗留一些条干边缘像素；当结构元素D的半径r为8，条干边缘的部分毛羽像素被腐蚀(见图5(d))。图5(c)显示，当圆盘结构元素D的半径r为6时，膨胀处理使纱线条干清晰，运算结果较好。

图5 不同圆盘半径时的膨胀处理图像Fig.5 Image of dilating operation with different disk radius

2.3 毛羽量统计

由于毛羽延伸方向的无规则性，使得扫描光照不匀造成同一根毛羽的不同部位和不同毛羽之间在图像中的亮度不同，且部分纱线毛羽和黑板背景之间边界不明。若采用全局单一阈值进行毛羽分割，将无法兼顾图像不同区域的实际情况，导致毛羽分割丢失。为提取整块黑板毛羽的完整信息，本文提出基于大津法(OTSU)的图像局部分割法分别对条干和非条干区域处理。

OTSU法[9]是采用最大类间方差法对图像中的像素用阈值分为目标和背景。根据式(1)、(2)计算得到最佳阈值。由于图像中纱线毛羽和背景之间差异较小，需选用合适的阈值分割，得到纱线与背景完全分离且不丢失毛羽信息的图像。

本文算法具体实现如下：首先，图像分成条干区域和非条干区域处理，将图像按12 像素 × 12 像素的窗口分块处理。对条干区域，按所设置的窗口检测到其中的像素值全部为1，即是条干部分，直接将其窗口内的像素值变为0储存在一个新矩阵Z中。对非条干区域，在子窗口中，提取所有非条干的像素点。为排除背景噪点对毛羽检测的影响，进行基于方差的毛羽分割。当窗口中非条干像素点的像素值方差大于5时，采用大津阈值对非条干像素点进行分割，结果存入矩阵Z中；若方差小于5，则说明窗口中存在于背景的噪点不是毛羽，直接将其像素值变为0存储在矩阵Z中。图6为图3(a)所示的纱线原始图像的毛羽图。图7为图2所示的9.83 tex纱线黑板局部采集图像的毛羽图。本文通过以上局部阈值方法实现了纱线毛羽的准确分割，完整地保留了黑板毛羽信息。

图6 毛羽分割图像Fig.6 Image of hairiness segmentation

图7 纱线黑板毛羽图Fig.7 Image of blackboard yarn hairiness

通过上述算法得到纱线毛羽二值图像，其基本单位是像素。遍历矩阵Z中所有非零像素点，即可得到图像中毛羽的数量：

(6)

式中：h(x,y)为毛羽分割后的图像；(x、y)为像素点的坐标；N1和N2对应于图像的大小，即N1为9 000像素，N2为10 800像素。

2.4 毛羽量M指数

由于图像法测得的像素值为黑板总的毛羽结果，该指标无法体现黑板上纱线单位长度的毛羽量。本节提出M指数作为评价黑板毛羽量的指标，为无量纲参数：

(7)

式中，Lm为黑板图像上长度为Ls(cm)纱段的当量毛羽长度，也就是将黑板图像上毛羽的像素点总数A换算成单个像素点为直径的毛羽长度，cm。

在本文实验条件下，M值为

1.12×10-6A

(8)

式中：(2.54×1 200)A为在1 200像素条件下的毛羽像素点总数的长度换算公式；Ls值为1 897 cm。

3 测试结果与分析

3.1 M指数与H值

Uster仪所测得的毛羽H值是指纱线上所有伸出纱线主体的纤维总长度与测量长度(1 cm)之比，为无量纲参数。样品单位测试长度为100 m。该结果可对照乌斯特统计公报查出相应的纱线毛羽水平，广泛应用于国内外纺织品市场[10]。

以表1中的18种纱线为试样。每种试样采集 10个纱线黑板图像，采用本文创建的测试和评价方法获得毛羽量M指数；同一试样的另10个纱线黑板图像经Uster仪检测后获得毛羽H值。18种试样的平均M指数和平均H值如表2所示。可知，18种试样M指数的CV值均小于4%，表明应用本文方法检测毛羽结果具有稳定性。

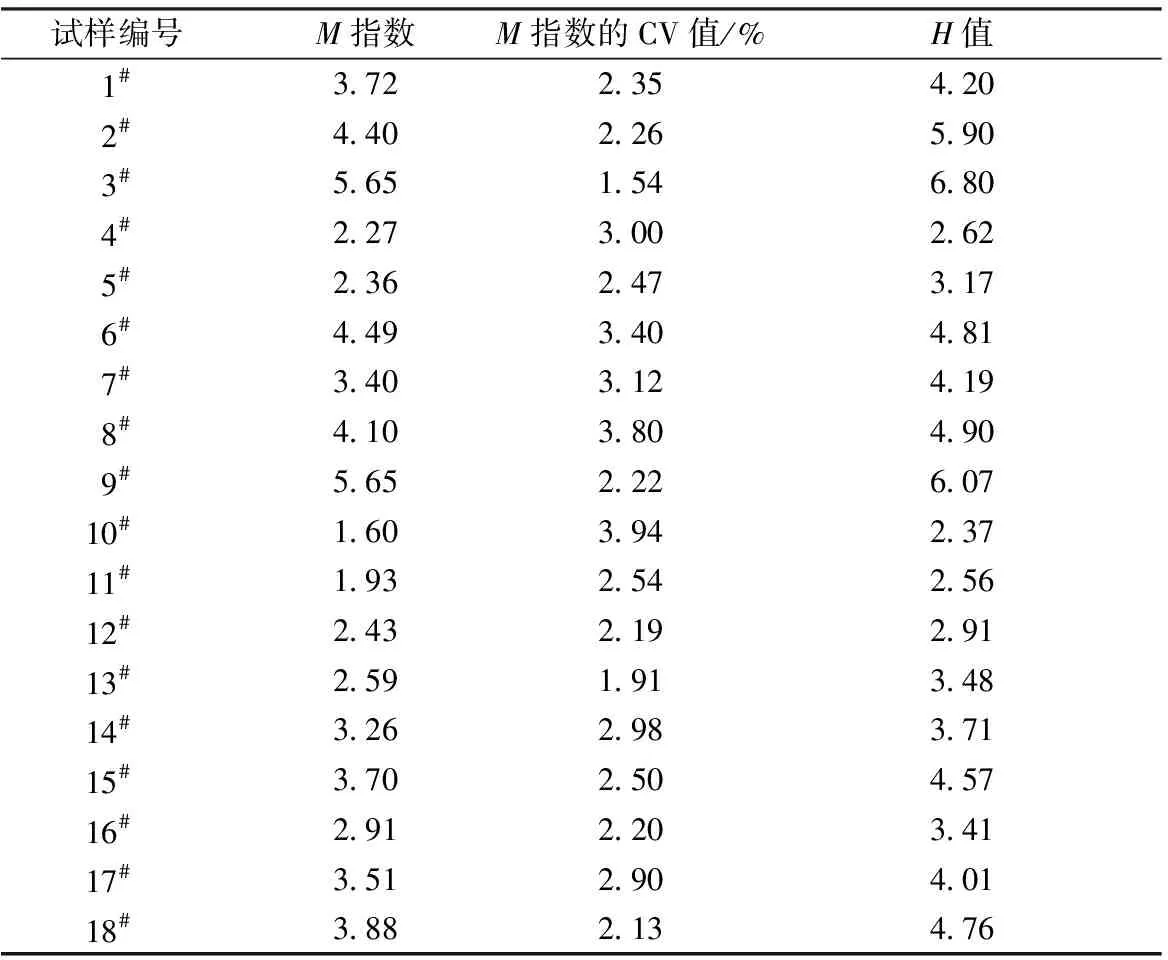
表2 M指数和H值的测试结果Tab.2 Test results of M index and H value

由表2可知，当原料和纺纱方式相同(如试样1#、2#、3#或4#、5#、6#或7#、8#、9#或10#、11#、12#或13#、14#、15#或16#、17#、18#)时，毛羽的M指数和H值的变化趋势相同，均随线密度的增大而增大；线密度为11.8 tex的环锭纺、紧密赛络纺和紧密纺的涤纶纱线(如试样8#、12#、18#)，纱线的毛羽量大小顺序依次为环锭纺>紧密纺>紧密赛络纺。

3.2 拟合方程

根据表2得到18种试样的M指数与H值的Pearson相关系数为0.972；sig.值均为0，差异极显著(p<0.01)，二者间有极强的正相关性，因此，设y为H值，x为毛羽量M指数，拟合方程见表3。

分析表3所得拟合方程可知，本文采用幂函数曲线作为M指数与H值关系的最佳曲线，其回归方程为

y=1.453x0.85

(9)

幂函数的可决系数R2最大，值为0.950，且相关系数R也最大，为0.975。表3中的拟合方程的显著性sig.值均为0.000，且所构建方程的相关系数都达到了显著相关水平。M指数与H值关系的拟合程度优劣可通过R2值来衡量，其值越接近1，优度越好。

表3 拟合方程综述表

从方程的F检验结果来看，式(9)的F检验值为304.193，相应的显著性小于0.001，回归方程非常显著。从回归系数的显著性检验来看，得到t检验值为17.441，相应的概率p值小于0.001，回归系数非常显著，表明本文所建立的幂函数回归方程有统计意义，2个变量之间相关关系显著，2种方法测得的毛羽量M指数与H值具有较好的可替代性，式(9)可作为毛羽H值的预测模型。

3.3 检 验

为检验纱线毛羽值预测模型的准确性，提取原料、纺纱方式、线密度不同的6种纱线的M指数，按式(9)计算得到毛羽预测值H′如表4所示。可见，毛羽预测值H′与Uster仪测得的毛羽H值的误差范围为1.78%～6.73%，因此，首先采用本文提出的基于图像处理的毛羽检测方法，然后采用评价黑板毛羽量的指标M指数、最终运用创建的毛羽预测模型，可有效预测毛羽H值。

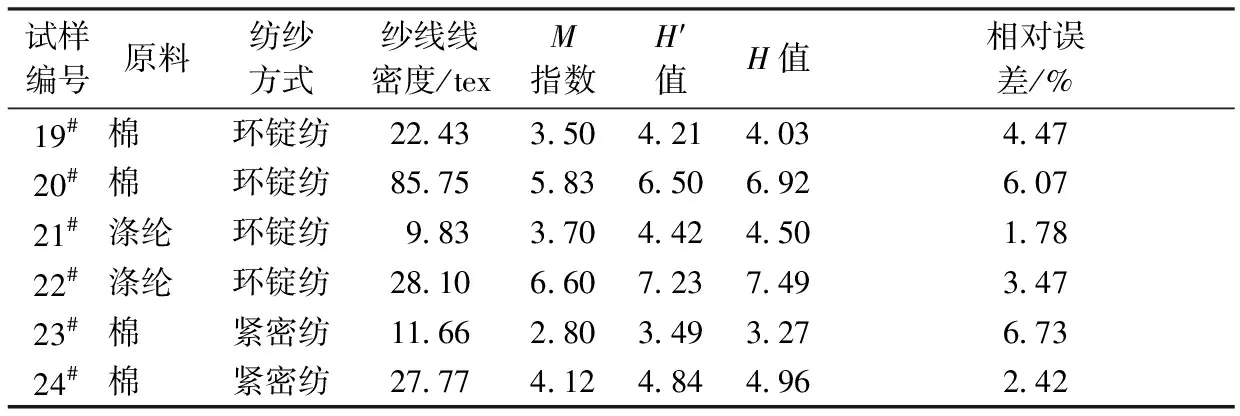
表4 毛羽H值与预测值H′Tab.4 H value and prediction results of H′

4 结 论

纱线毛羽是反映纱线质量的重要指标之一。本文针对主观评价的不足，建立了一种新的客观评价方法，结论如下：

1)提出了一种基于图像处理的纱线黑板毛羽量检测方法；即通过中值滤波、二值化处理、形态学运算、图像分割等图像处理技术获取毛羽量像素值。

2)提出了评价纱线黑板毛羽量的新指标M指数，建立了纱线黑板毛羽值预测模型。

3)采用本文建立的基于图像处理的毛羽量检测方法，并应用构建的毛羽值预测模型，可较准确地预测毛羽H值，客观评价毛羽水平。