热辐射下织物内水分干燥实验及其动力学研究

陈 萌， 朱方龙

(中原工学院 服装学院， 河南 郑州 450007)

暴露于高湿度环境中，多孔隔热织物易于吸收水分，高温受热后其水分蒸发过程的潜热会影响到织物整体的隔热防护性能，因此，有必要研究热作用下织物内水分迁移过程及特性[1-3]。Rossi等[4]分析了热蒸气在不同类型织物层中的传递过程，得出水蒸气在织物内传递取决于样品的厚度、渗透能力及其隔热能力；Weder 等[5]使用X射线断层摄影术研究了不同织物层的组合对水分分布的影响，结果发现大部分水分累积在接近皮肤的2层织物中；文献[6]采用实验方法对直接接触火焰的湿态多孔介质进行分析，数据显示，适量的水分蒸发可略微增强其热防护能力；Schneider 等[7]采用瞬态测试技术测量了不同水分含量的纺织品的有效导热系数，其值随含水量增加而增加，同时纤维本身的吸附性能也影响其有效导热系数值。

同时，已有的研究工作也提出了热流作用下多孔织物内热湿传递行为数学模型，解析湿分在织物中的迁移机制：Li 等[8]发展了水分吸附作用、凝结作用与热传递相耦合的热湿传递模型，其模型预测值与实验结果吻合良好；文献[9]介绍了涵盖液态水和水蒸气传递的湿分传递模型，并包含了多孔介质内液态水传输的毛细管效应；Zhu 等[10]首次应用一步式阿伦尼乌斯化学反应速率方程模拟了火场环境下织物水分干燥过程，建立了考虑织物热参数随温度变化的模型本构方程。

食品及生物质材料的干燥过程研究已相当成熟，很多文献提出了不同模拟条件下的干燥曲线模型[11-13]，研究了固体干燥过程参数和水分传递参数[14-17]，大部分生物质材料由纤维素纤维构成，因此，已经提出的干燥模型可借鉴用于描述纤维素纤维织物甚至是化学纤维织物的干燥曲线。本文采用干燥动力学理论来描述较低辐射热暴露下织物水分传递特性，并以织物表面的温度变化来评价织物整体隔热性能与水分之间的关系。对合适的多孔织物干燥动力学模型进行评估，验证实验数据与等温干燥模型的匹配程度。

1 实验部分

1.1 试样与性能测试

实验采用3种常用消防服外层织物，由上海圣欧同安防护用品开发有限公司提供，其基本参数如表1 所示。每种织物准备3块样品 (130 mm× 130 mm)，将样品放至于温度为105 ℃的烘箱中干燥 2 h，确定样品的干态质量(F-1、F-2、F-3分别为 3.28、5.91、3.54 g)，然后将与织物干态质量相同的水分均匀喷洒至样品上，获得初始含水率100%的织物。为模拟消防员在火场救援过程中消防服被喷湿的情形，在到达设定含水率为100%后即刻开始实验。实验开始时织物中同时存在3种形式的水：吸附水、毛细水和自由水。3种水的比例因织物样品吸湿性的不同而不同。

表1 织物规格参数表Tab.1 Fabric specification parameters

实验采用如图1所示的自制设备，由石英灯管辐射热源、电子天平(精度为±0.01 g)、红外热像仪及数据采集模块4部分组成。实验在0.4 kW/m2和0.8 kW/m22种辐射热源下进行，织物与热源表面距离为23 cm，织物质量和温度的变化分别用WT2102型纺织天平和Fluke Ti32 型红外热像仪测量。

织物含水率和干燥速率分别由式(1)、 (2)计算得到。

M=(mw-md)/md

(1)

N=-dM/dt

(2)

式中：M为干基含水率，%；mw为湿态质量，g；md为干态质量，g；N为干燥速率，%/s；t为时间，s。

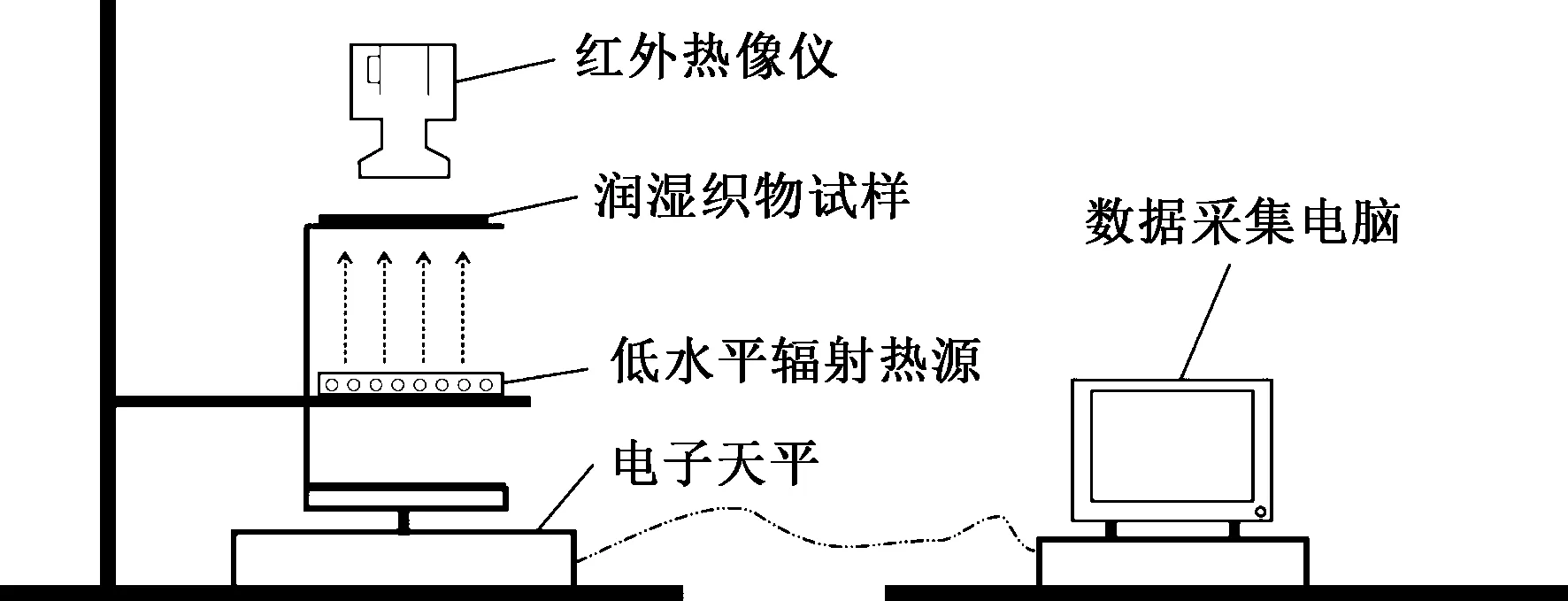
图1 实验装置整体示意图Fig.1 Overall sketch of experimental installation

织物的相对含水率R(无因次含水率) 由式(3)计算：

R=(Mt-Meq)/(M0-Meq)

(3)

式中：Mt为任意时刻t的回潮率，%；M0为样品初始含水率，%；Meq为样品平衡含水率，%。织物在干燥最后状态其Meq值为0，那么式(3) 可简化为

R=Mt/M0

(4)

1.2 数学模型

干燥过程中水分扩散可由Fick方程描述，为简化方程，给出如下假设：1) 织物层中水分的初始分布是均匀的，并假定湿润织物层在纤维排列和材料性能上是各向同性的；2) 织物层中水分的流动阻力分布均匀；3) 扩散系数与部分含水率无关；4) 忽略纤维体积因含水率变化而产生的变化。基于以上条件Fick第二定律可写成式(5)[18]:

(5)

式中：D为扩散系数，m2/s；x为扩散距离，m。

因为假定织物的水分含量在初始阶段分布均匀，且质量输运是一维的，织物表面的水分可以与周围瞬间达到平衡，因此，薄层织物的初始和边界条件可描述为：

(6)

然后求出式(3)的级数解，即

(7)

式中，L为材料层厚度的一半,m。

假设干燥时间足够长，第1项就可准确地预测无因次含水率，即

(8)

式(8)可进一步被简化成线性方程

(9)

式中，Deff为有效湿汽扩散系数，m2/s。

另有研究者也基于式(8)提出了修正方程。选取表2所示的已有模型，用于干燥实验数据的分析比较，优选适合于描述织物干燥过程的预测模型。

表2 干燥模型

2 结果与讨论

2.1 织物的干燥曲线

将织物的质量损失转化为其干基含水率(后文简称为“含水率”)的变化，然后绘制“时间-含水率”变化曲线，图2～4分别示出2种不同强度辐射热源下的3种织物的含水率与温度随时间的变化曲线。

图2 辐射热暴露下的F-1试样含水率及温度变化Fig.2 Moisture content and temperature variations of F-1 under radiant heat exposures

由图2～4可看出，在2种不同的热辐射条件下，3种织物的含水率均随时间的延长而下降，所有的干燥曲线包括3个阶段(见图5)：第1阶段，水分含量变化不大，温度迅速上升，辐射热主要用于加热织物；第2阶段，水分含量迅速下降，温度缓慢上升，在该阶段辐射热主要用于织物中的水分蒸发；第3阶段，水分含量缓慢下降，当含水率下降到20%后，温度突然升高，然后慢慢上升。3个阶段的划分如图5所示。这说明当织物含水率大于20%时，水分蒸发所消耗的能量延迟了织物温度的升高；然而当水分含量降低至20%时，这种能量消耗就会明显下降，导致温度迅速上升。在此阶段，一部分辐射热流量将用于水分蒸发，另一部分热量被织物吸收，导致织物表面温度上升。

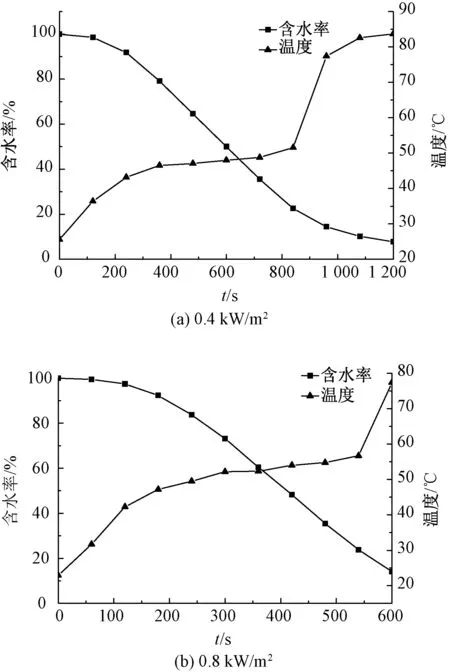
图3 辐射热暴露下的F-2试样含水率及温度变化Fig.3 Moisture content and temperature variations of F-2 under radiant heat exposures

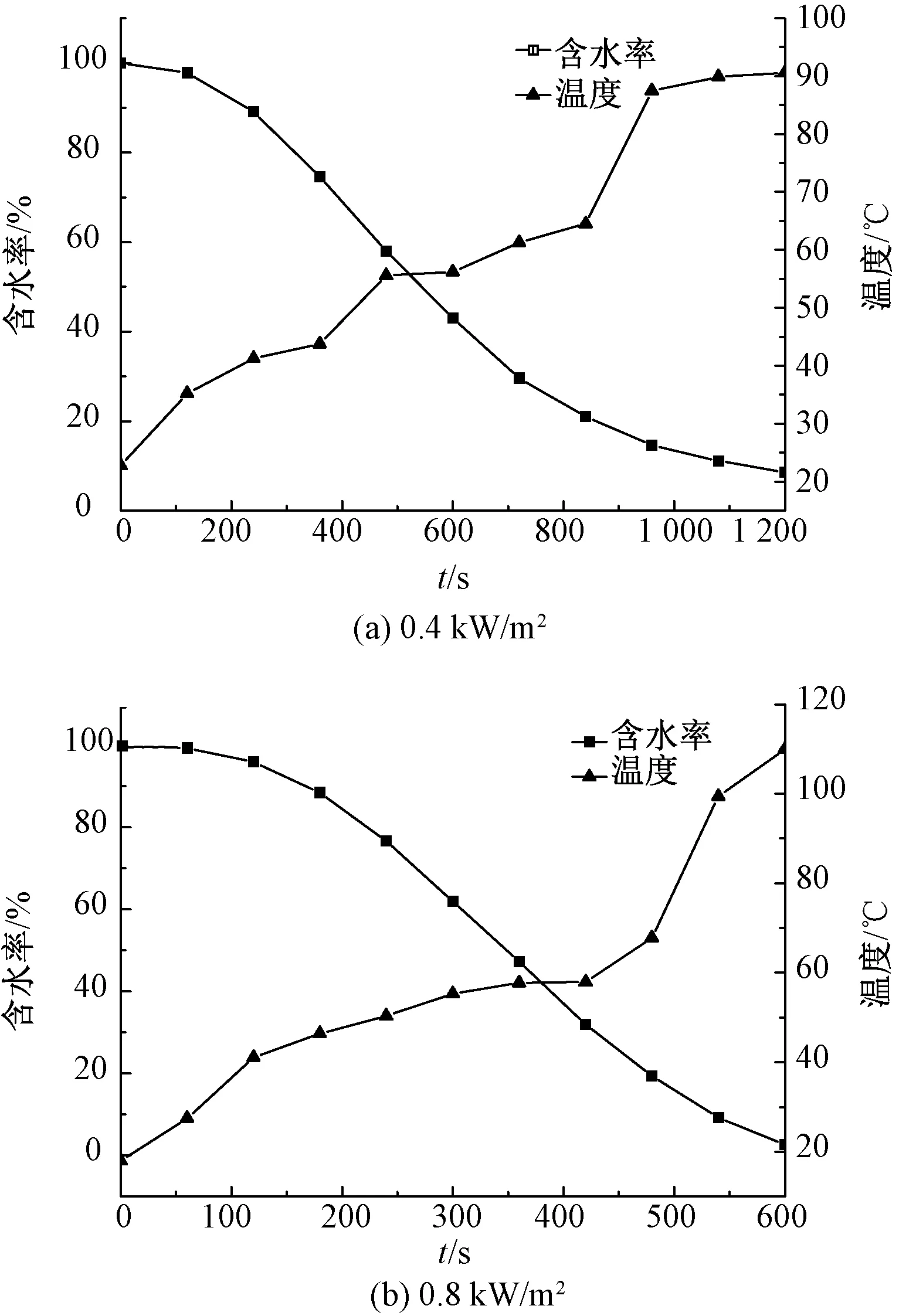
图4 辐射热暴露下的F-3试样含水率及温度变化Fig.4 Moisture content and temperature variations of F-3 under radiant heat exposures

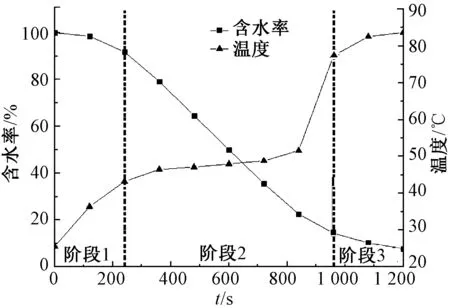
图5 3个干燥阶段的划分Fig.5 Division of three drying stages

3种织物试样在2种辐射热条件下的干燥曲线如图6所示。可知，织物试样的干燥速率在开始阶段上升，很快进入相对稳定阶段，但稳定时间较短；最后，干燥速率下降。这与含水率变化的3个阶段是吻合的。比较图6(a)、(b)知，3种织物在 0.8 kW/m2的热源下干燥速率高于0.4 kW/m2热源下的干燥速率。

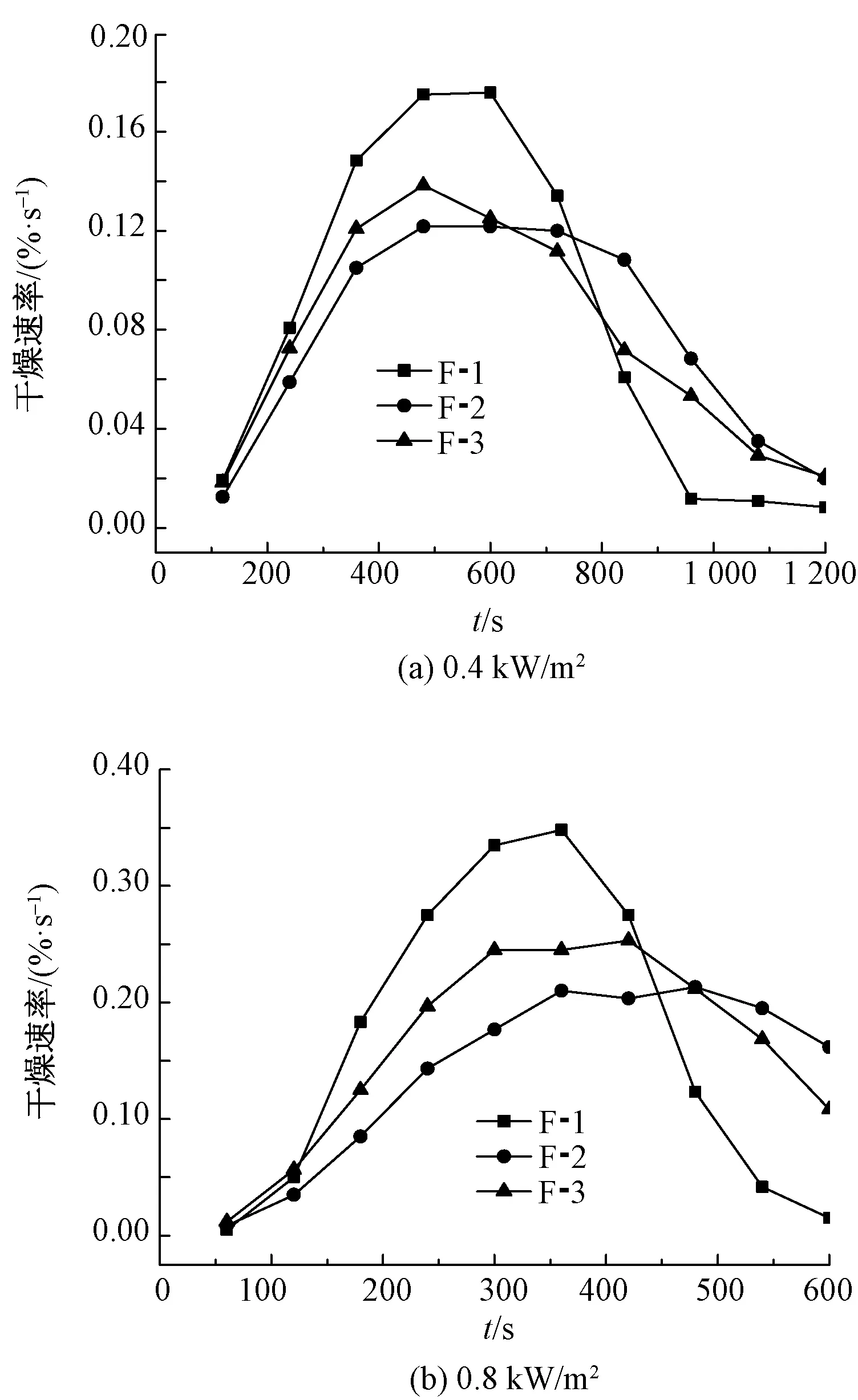
图6 3种织物样品的干燥速率Fig.6 Drying curves of three kinds of fabric specimens

2.2 干燥动力学模型

图7示出3种织物试样在2种不同辐射热流量下的ln (-lnR)与lnt关系图。可以看出，ln (-lnR) 和 lnt之间存在确定的线性关系，假设其线性关系如式(10)所示：

ln(-lnR)=lnk+nlnt

(10)

即：

R=exp(-kn)

(11)

式中，k和n为待定系数。

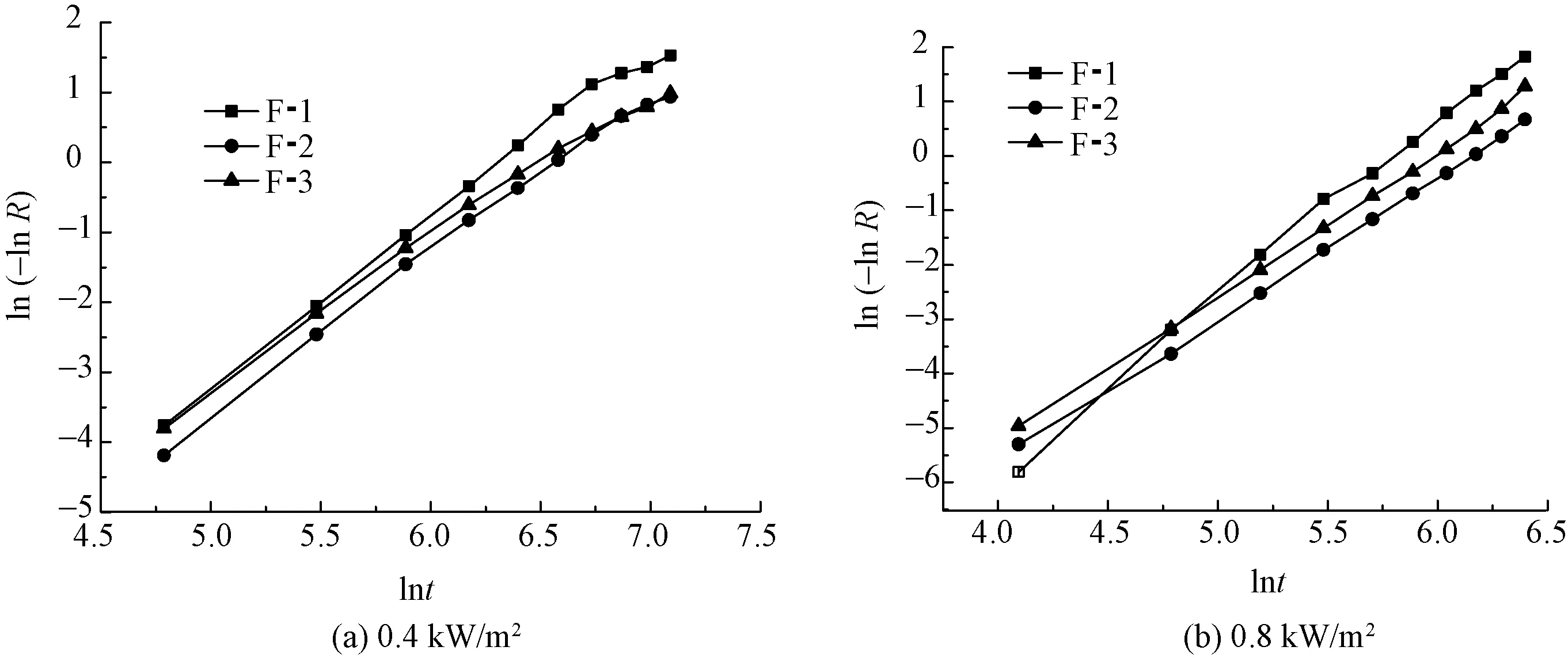
图7 ln (-ln R) 与 lnt的关系图Fig.7 Relation diagram of ln (-ln R) and lnt

干燥动力学参数由SPSS 17.0软件计算，结果如表3所示。

表3 不同辐射热流量时的干燥动力学参数Tab.3 Drying kinetic parameters at different radiation heat flow

图8示出2种不同辐射热条件下试样的- lnR与t的关系。可见，t和lnR之间不存在线性关系，因此，Newton 模型和 Henderson 模型不能应用于织物的干燥动力学研究。

图8 不同辐射热流时lnR与 t 的关系图Fig.8 Relation between lnR and t at different radiation heat flow

为验证根据Page模型所获得模型的准确性， 将F-2在0.8 kW/m2的干燥条件下的无因次含水率的实验值和Page模型计算值在同一张图中绘制，如图9所示。根据得到的模型，实验值和所获得模型的计算值有很好的一致性，表明Page方程可准确地预测织物的无因次含水率和热辐射时间的关系。

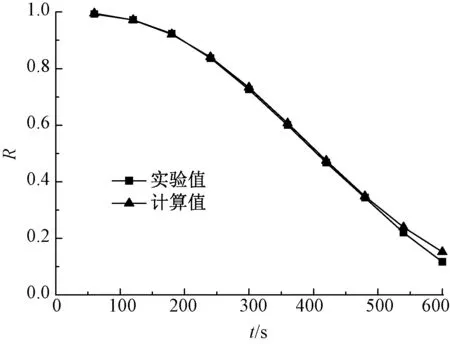
图9 无因次含水率的实验值与模型计算值的比较Fig.9 Comparison of experimental value and calculated value according to obtained model

3 结 论

在低热辐射条件下，湿态单层织物的干燥过程分为3个阶段：第1阶段，干燥速率和织物的温度快速上升，含水率缓慢下降；第2阶段，干燥速率保持稳定，织物温度缓慢上升，含水率快速下降；第3阶段，干燥速率下降，含水率缓慢下降。另外发现，当含水率大于20%时，水分蒸发要消耗大部分的能量，这延迟了织物的温度上升，但是一旦含水率下降到20%，水分蒸发所需要的能量消耗明显下降，导致织物温度快速上升。

织物F-2在0.8 kW/m2的干燥条件下的无因次含水率的实验值和Page模型的计算值之间有很好的一致性，表明Page模型可以通过选择合适的参数来预测低水平辐射热暴露下的润湿的多孔织物的“质量-时间”变化，研究结果对在低热辐射条件下水分扩散的预测具有一定的参考价值。