基于ANSYS软件中概率设计系统模块的综合管廊可靠性分析

，，

(1.中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580；2.东营铁能岩土工程有限公司，山东 东营 257000)

综合管廊是在城市地下用于集中敷设电力、通信、给水、热力、燃气等市政管线的公共隧道[1]。目前管廊结构的设计方法是基于结构力学和材料力学来计算并选取相应的结构材料和尺寸的，这种设计方法缺乏对影响结构稳定性的参数的考虑，在选用管廊结构材料时通常会出现浪费的现象，不利于设计出新型、高效、稳定的综合管廊结构。本文中基于ANSYS软件对管廊结构进行可靠度分析，基于结构可靠性理论和ANSYS软件的概率分析功能，结合实际工程，将综合管廊宽度、弹性模量等作为随机输入变量，选取拉丁超立方分析方法进行可靠度分析。

1 结构可靠性理论

可靠性是指建筑结构物在一定情况下能够正常实现使用性能的特性。可靠度是结构在规范规定的时间内和状态下达到既定功能的概率。当整个或结构某一部分超过某个状态而不能满足规范设计要求时，该状态为极限状态。结构的极限状态采用极限状态方程[2]来描述,即

Z=g(X1,X2,…,Xn)=0，

式中：Xi(i=1,2,…,n,n∈+)为影响结构的基本变量；Z或g(·)为结构的功能函数。

结构极限状态方程中的基本变量包括外荷载、材料和结构几何参数等随机变量。功能函数主要有2个变量，即结构抗力R、荷载效应S。S分为恒荷载Sg和活荷载Sq，则功能函数可以表示为Z=R-S=R-Sg-Sq，其极限状态方程为Z=R-S=R-Sg-Sq=0。 如果Z>0,则结构满足要求；如果Z<0，则结构不能满足可靠性要求；如果Z=0，则结构在极限平衡内并位于临界点。

2 ANSYS软件的概率分析功能

2.1 蒙特卡罗法

在概率分析中经常用到蒙特卡罗法，它能较清楚地模拟实际问题。用蒙特卡罗法计算随机问题时，重点是依据变量的分布情况生成随机数。一般先得到在(0,1)分布的随机数，然后经过一个合适转化，求得所要的随机数。依据状态变量x1,x2,…,xm(m∈+)的函数f1(x1),f2(x2), …,fm(xm)，在电脑上分布生成各类型的一组随机数抽样值…,代入功能函数即可获得Z的一个随机数，显然Z可理解为从概率密度中抽得的一个样本。重复以上步骤n次，能够获得随机变量Z的一个容量为n的样本。求解结构的可靠概率时，可以直接算出样本数m∈+，在n足够大时，频率已经近似于概率，因此能够获得结构的可靠概率

2.2 拉丁超立方抽样

拉丁超立方抽样(LHS)技术比蒙特卡罗法更先进、有效。 LHS法与直接法的唯一不同之处是LHS法具有抽样记忆功能，可以防止蒙特卡罗法中数据点集中所导致的仿真循环次数增多的问题[3-8]。 同时，该方法在抽样过程中抽样点必须离散分布于整个抽样空间。 一般情况下，对于相同问题要得到相同精度的结果，LHS法比蒙特卡罗法要少20%～40%的仿真循环次数(循环次数的大小不是人为指定的，而是由问题本身决定的)，因此本文中采用LHS法。

3 基于ANSYS软件的可靠性分析

计算结构可靠度是指计算极限状态函数Z>0的概率值。以结构静力分析结果为基础，综合考虑存在的一些相关不确定性变量因素，然后应用可靠性计算分析方法对最大应力强度值和最大位移进行可靠性分析。在使用管廊正常工作的过程中，禁止发生结构受到的最大应力值大于材料强度值以及结构的最大位移大于允许位移限值的现象。

3.1 具体实例

3.1.1 工况分析

某段综合管廊全长12.8 km，管廊标准断面采用4舱通行管沟结构(分为污水舱、水力舱、电力舱、天然气舱)，设计结构标准断面内尺寸为13.85 m×4.6 m(长度×宽度)，如图1所示。

计算所涉及的材料主要是岩土、钢筋、混凝土，钢筋材料型号为HRB400、HPB300，混凝土强度等级为C45，钢筋和混凝土材料参数取值见表1、2。该段开挖深度为8 m，土断面示意图如图2所示。地下水位取地下0.5 m。

表1 混凝土材料参数

表2 钢筋材料参数

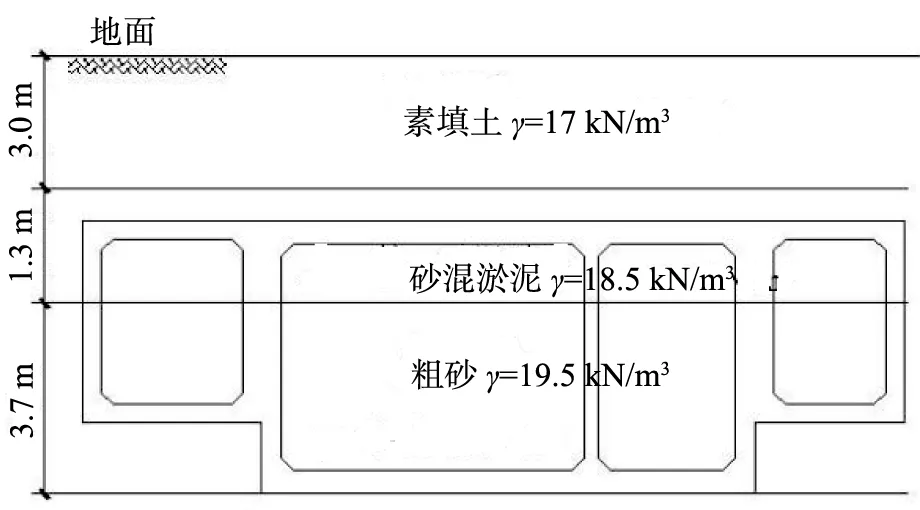
γ—土天然重度。图2 土层横断面

该段管廊承受的荷载分为永久荷载和可变荷载。永久荷载包括土重力、水压力、土侧压力、结构自重；可变荷载是人和车辆荷载。结构荷载分布如图3所示。

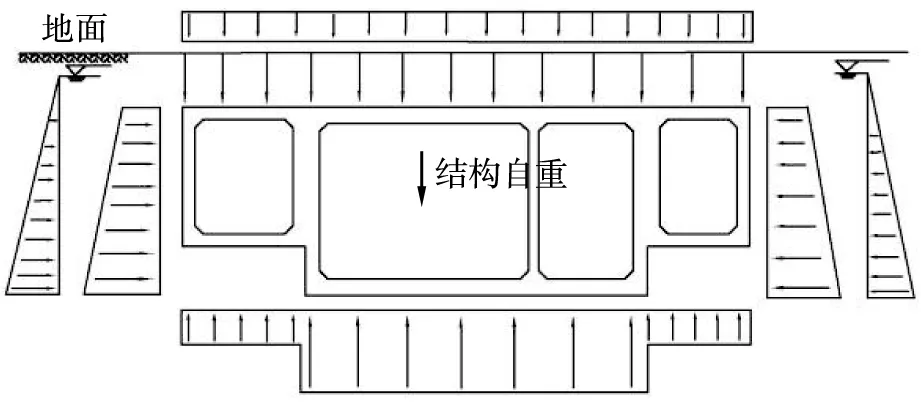
图3 结构荷载分布

3.1.2 数值模拟

截取该工程标准段建立管廊模型，截面如图1所示，管廊模型尺寸为13.85 m×4.6 m×20 m(长度×宽度×高度)。管廊采用Solid单元建模，Solid 65单元可以较好地模拟混凝土、岩石等非均匀材料的拉裂和压碎现象。

经数值模拟计算，得到管廊应力分布和位移分布云图，如图4所示。由图4(a)可知，管廊各舱室下腋角处均出现应力集中现象，其中水力管线舱和电力管线舱的下腋角应力集中现象最明显。由图4(b)可知，管廊整体变形趋势呈凹字形，管廊底板不变形，顶板变形由中心向左右两边均匀减小，水力管线舱顶板中心位移最大。

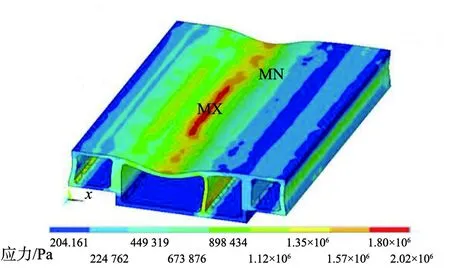
(a)应力分布

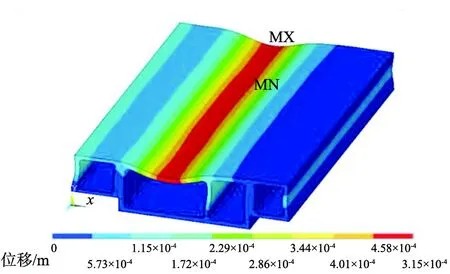
(b)位移分布MX—应力最大值；MN—应力最小值。图4 综合管廊应力分布和位移分布云图

3.2 结构可靠性计算

ANSYS软件中概率设计系统 (possibility design system, PDS) 模块将可靠性设计理论与有限元分析技术相结合，在模块内选取执行文件，然后设定输入变量及输出变量。本文中选用LHS法进行分析，连续进行500次重复循环运算，然后进行可靠性分析。假定输入变量都服从正态分布,其均值和标准差如表3所示。选取单元建立模型，施加载荷，分析计算结束后进入PDS模块，选取LHS法并设置500次分析，最后将最大位移赋值给位移最大值DMAX，将最大应力赋值给应力最大值SMAX。

表3 输入变量及其均值和标准差

3.3 模拟结果精度检验

图5所示为管廊结构最大应力的抽样均值趋势，其中，中间的曲线代表抽样均值，上、下2条线之间表示抽样的范围。由图可知，随着抽样次数增加，均值曲线趋于平缓，表明500次采样满足可靠性要求。最大等效应力的抽样均值为2.24 MPa，标准差为0.2 MPa。

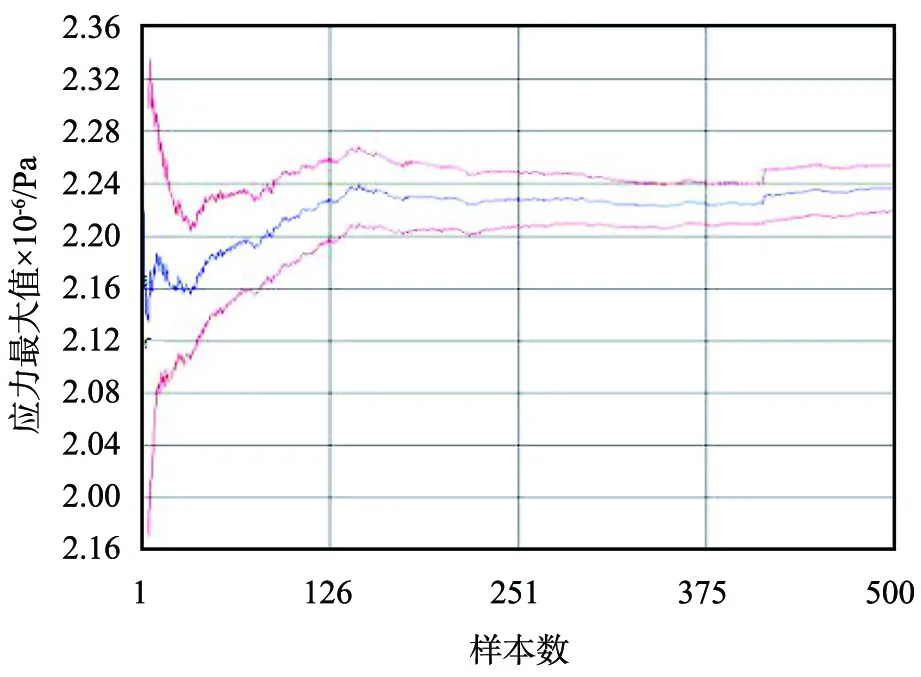
图5 管廊结构最大应力抽样均值趋势

图6所示为管廊结构最大应力的累积概率分布。 由图可知，当置信度为95%时，结构最大应力小于4.75 MPa的概率为99.99%，结构失效概率为0.01%，而结构材料允许承载力为45 MPa，大于4.75 MPa，说明结构强度达到规范要求。

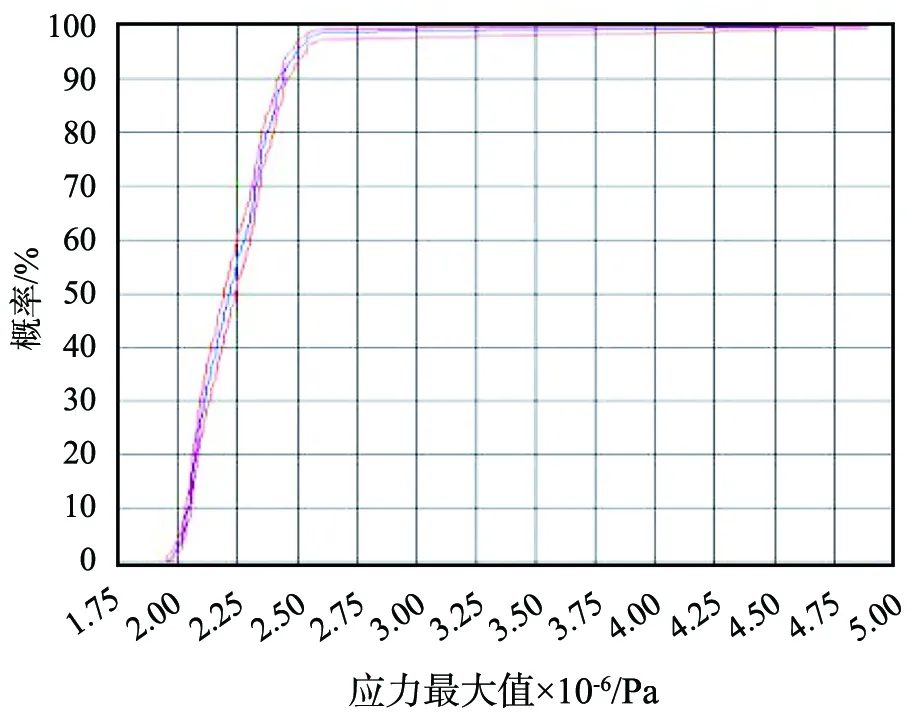
图6 管廊结构最大应力的累积概率分布

图7所示为各随机变量对管廊结构等效应力的影响程度。由图可知，各随机变量对最大应力影响最大的是泊松比，其次是管廊宽度和弹性模量，其他因素如管廊的宽度和长度对应力影响较小。

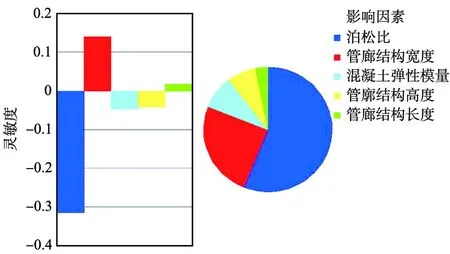
图7 各随机变量对管廊结构应力的影响程度

管廊结构最大位移抽样样本均值趋势如图8所示。由图可知，样本均值曲线趋于平缓，说明所取抽样足够。最大位移的均值为0.66 mm，标准差为0.03 mm。

图8 管廊结构最大位移抽样均值趋势

管廊结构最大位移的累积概率分布如图9所示。 由图可知，当置信度为 95%时，最大位移小于1 mm的累积概率为99.99%，所以结构失效概率为0.01%，结构位移允许限值为25 mm，远大于该结构可能的最大位移值，说明强度符合规范要求。

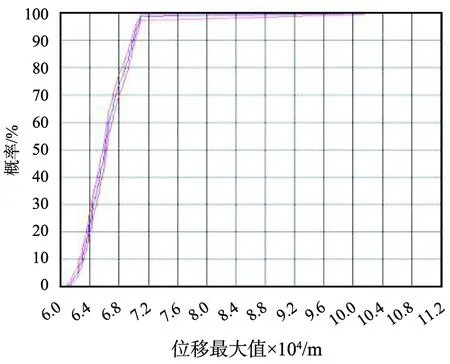
图9 管廊结构最大位移的累积概率分布

图10所示为各随机变量对管廊结构位移的灵敏度。由图可知，图中管廊的宽度对结构位移的灵敏度最高，混凝土弹性模量和管廊高度次之，其他变量对结构位移的影响较小。

图10 各随机变量对管廊结构位移的影响程度

4 结论

本文中基于ANSYS有限元软件，将综合管廊的各设计参数作为随机变量，得出了管廊结构的最大位移和最大应力均远小于设计值的结论，该结论说明结构设计有进一步优化空间，应避免产生材料浪费的现象。管廊各个舱室内壁下腋角处出现明显的应力集中现象，在结构设计时应适当增加腋筋配筋率。以上基于ANSYS软件的可靠性分析可以为管廊结构的优化提供基础，并为管廊结构设计方法的更新提供借鉴。