移动载荷作用下周期性高架桥有限元模型
,,
(1.江苏大学 土木工程与力学学院,江苏 镇江 212013; 2.东南大学 成贤学院,江苏 南京 200092)
目前,高架桥已经成为高速铁路的一种重要结构形式。在列车移动载荷作用下,高架桥动力响应的研究对高架桥的设计及维护有重要意义,因此前人对结构在移动载荷作用下的动力响应已开展了大量研究[1-2]。为了便于施工,正常路段的高架桥通常设计成等跨距形式,因此,高架桥可以简化为周期性结构。近年来,随着理论和计算技术的发展,学者们在周期性结构对移动载荷的动力响应方面开展了一些研究,并建立了求解此类问题的一些半解析及数值方法。 文献[3-4]中最早提出了周期支撑的三维轨道模型,弹性半空间上的Euler-Bernoulli梁对移动荷载的动态响应进行研究。 刘维宁等[5]考虑了动力互等定理,对周期轨道结构在半无限弹性空间体上受移动荷载作用的问题进行了相应研究,通过叠加周期解析计算出无穷积分。 刘维宁等[6]通过Laplace变换和传递矩阵(transfer matrix,TM)法研究了周期支承轨道对移动荷载的动力响应。 Chebli等[7]利用系列Fourier变换方法,建立了求解周期性结构对移动载荷的动力响应的一种新方法,该方法能将整个周期性结构的求解简化为求解其中一个单元,大大减少了计算量。 Sheng等[8]将不平顺轨头的周期设置成轨枕间距的整数倍,然后采用Fourier级数法研究不同数量的匀速移动荷载下轮道之间的相互作用力。 文献[9-10]中根据辛数学法研究了周期不平顺轨道与车辆的耦合系统的随机响应。 Lu等[11]利用TM法和系列Fourier变换方法,建立了周期性简支梁型高架桥的力学模型,得出周期性高架桥(periodic viaduct,PV)的特征方程以及高架桥对单个移动荷载的动力响应,对波在某一跨的传播进行分析得出整个周期性高架桥的动力响应。
由于文献[11]中建立的TM法仅适用于均质的周期性高架桥结构,对几何或材料非均质的周期性高架桥结构,该法很难应用,因此,需要建立计算PV对移动载荷动力响应的有限元模型。为了建立上述有限元模型,本文中首先采用Fourier变换方法,得出移动载荷的频率波数域表达式,利用PV代表性跨的有限元方程,并结合简谐荷载作用下PV的周期性条件,可得PV受频率波数域内单位简谐荷载作用下的动力响应,对PV的频率波数域内的响应进行相应的Fourier逆变换,即得PV在移动载荷作用下的动力响应;基于所建立的有限元模型,给出一些算例。
1 PV的简化力学模型
将高架桥简化为周期性结构,如图1所示。高架桥每跨只由1个桥墩构成,并且桥墩底部均为刚性连接。每跨上部结构由左梁、右梁、梁-梁连接弹簧、左梁-墩连接弹簧和右梁-墩连接弹簧组成。其中3根弹簧和其所连接的左梁、右梁和墩的端部构成梁-梁-墩(beam-beam-pier, BBP)接头。假设坐标原点如图1所示在0跨BBP接头的中心,左梁、墩和右梁分别用a、b和c表示,梁-梁弹簧、左梁-墩弹簧和右梁-墩弹簧分别用t、l和r表示。
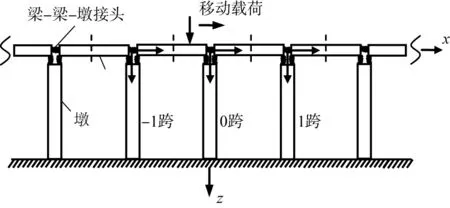
图1 周期性高架桥受移动载荷作用
本文中将移动载荷简化为垂直分量和水平分量力,因此图1就是简化的PV对移动载荷的动力响应的有限元模型。
2 移动载荷作用下PV动力响应表达式
本文中的研究会涉及到时空内的Fourier变换。对时域内的函数,其Fourier变换可定义为
(1)
式中:ω为圆频率;t为时间;上标~表示为频域内的变换。对空间域函数,Fourier变换可定义为
(2)
式中:x为空间变量;k为波数;上标^表示为波数域内的变换。
当移动荷载在x轴上以速度v运动,其表示为
f(x,t)=f0δ(x-x0-vt),
(3)
式中:δ为狄拉克函数;f0为移动荷载的幅值;x0为0时刻荷载的坐标。对式(3)进行时空域Fourier变换,得载荷频率波数域内的表达式为
2πf0eikx0δ(kv-ω)。
(4)
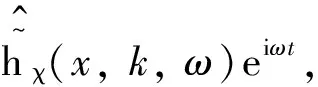
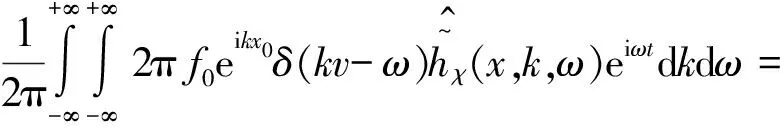
(5)
式(5)表明,在移动荷载作用下,PV频域内的响应为
(6)
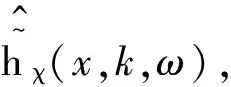
3 单位简谐荷载作用下PV的动力响应
3.1 梁及墩的控制方程
如图1所示,移动荷载作用下PV的梁和墩发生轴向振动和弯曲振动。根据Euler-Bernoulli梁理论,梁和墩的弯曲振动和轴向振动的控制方程为
(7)
根据标准线弹性固体模型,构件材料的复模量[12]可表示为
(8)
式中:Eα1和Eα2为标准固体模型的弹性参数;ηα为黏滞系数。
3.2 单跨的有限元方程
3.2.1 梁及墩的有限元方程
本文中梁和墩均用两节点的单元来离散,任一单元的2个节点分别用i和j来代表,构件α包含Eα个单元和Nα个节点,Nα=Eα+1。各个构件都包含2个端部节点和Nα-2个内部节点,下文中接头节点表示为3个构件连接弹簧的端部节点,而内部节点表示为I, 其+I(I+)表示为两梁左(右)端节点以及墩顶(底)部节点和其内部节点的集合。
由于梁和墩都会产生轴向弯曲和振动,并且节点具有3个自由度,因此梁和墩位移向量可表示为
(9)
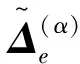
根据虚功原理[13],得出单元有限元方程
(10)
(11)
3.2.2 BBP节点处的连接条件
(12)
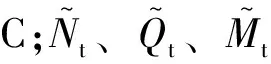
(13)
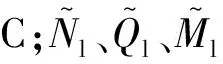
(14)
(15)
式中T1和T2表达式见附录C。同理,墩顶处节点的集中等效节点力向量的表达式为
(16)
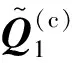
(17)
利用式(12)—(14),方程(15)—(17)可改写为
(18)
式中弹簧刚度矩阵S表达式见附录C。
3.2.3 单跨的有限元方程
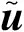
(19)
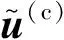
(20)
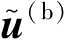
(21)
在建立的有限元方程中,设节点的顺序为左梁的全部节点、墩节点(除墩底节点外)及右梁的全部节点、墩底节点。其中梁节点的编号顺序是沿x轴正方向,墩节点的编号顺序是沿z轴正方向。建立整体有限元方程
(22)
式中K和M为PV单跨刚度矩阵和质量矩阵,表达式见附录D。将式(18)代入式(22),得到单跨的有限元方程
(23)
3.3 单位简谐荷载作用下PV的动力响应
将整跨节点划分为左节点、内部节点、右节点和底部节点4个部分,则整跨位移向量可以表示为
(24)
(25)
单位简谐荷载ei(ωt-kx)作用下,PV的相邻跨左端的位移和集中力向量之间相位差为e-ikL(L为梁的长度),则各跨左端和右端的位移和集中力向量有如下关系:
(26)
(27)
式中λ=e-ikL。
4 验证及算例分析
为了验证本文中建立的有限元模型,材料参数的选取与文献[11]中一致。将PV第0跨左截面频域内响应与文献[11]中采用TM法得到的响应结果进行对比。图2给出了2种方法所得的移动载荷速度为100、150 m/s时所引起的第0跨左截面频域内剪力。从图可以看出,2种方法得出的的结果比较吻合,因此验证了本文中建立的有限元模型。
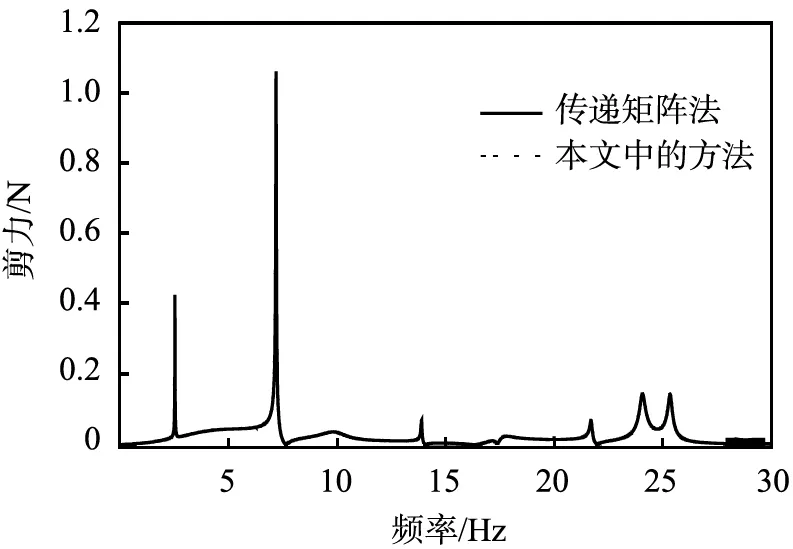
(a)移动载荷速度为100 m/s时的剪力
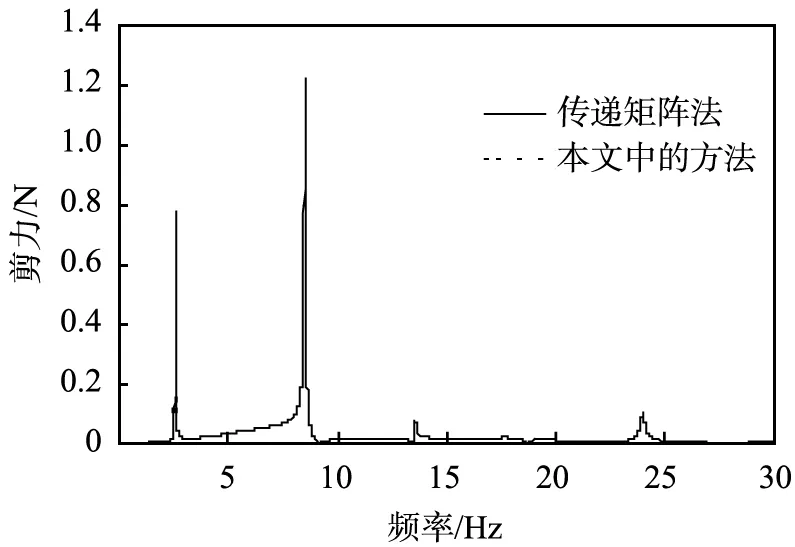
(b)移动载荷速度为150 m/s时的剪力图2 有限元法和传递矩阵法所得到计算跨左截面频域内剪力的比较
本文中PV计算跨的参数确定源于文献[15-19]中选取,如表1所示。PV的梁截面等效为矩形截面,墩截面等效为圆形截面,梁的弹性模量取C30。梁间轨道刚度是根据轨枕间隙长度确定,支座弹簧刚度是根据经验数据和文献[20]中橡胶支座刚度确定,且左梁-墩的连接弹簧和右梁-墩的连接弹簧刚度不同,具体数值见表2。

表1 梁墩的计算参数

表2 梁-梁、左梁-墩和右梁-墩的弹簧刚度的取值
在计算中,PV的左梁、右梁和墩均划分为100个相同有限单元。由于当频率大于30 Hz时PV的动力响应很小,因此本文中只给出了频域在30 Hz内的结果。 计算跨取PV的第100跨,当移动载荷速度为50 m/s时频域内采12 001个样点数,相应的时域内计算范围为0~500 s;当速度为100 m/s时频域内采9 001个样点数,相应的时域计算范围为0~300 s。
图3给出了移动载荷速度为50、100 m/s时计算跨左端截面频域内的剪力值。从图中可以看出,速度不同,剪力共振峰的个数明显不同,虽然都处在第二通带内,但速度为50 m/s时共振峰的个数要多于速度为100 m/s时的。图4给出了移动载荷速度为50、100 m/s时计算跨左端截面时域内的剪力值。结果表明,荷载的速度对高架桥的时域内响应有显著影响,对于速度为50、100 m/s这2种情形,荷载通过计算截面时,2种情形的剪力值很接近,但是,当速度为100 m/s时,剪力衰减较快。此外,速度为50 m/s时高架桥的响应几乎与载荷的到达时间对称,但是,当速度为100 m/s时,高架桥的响应出现类似冲击波特征,即高架桥在载荷到达前无明显的响应。
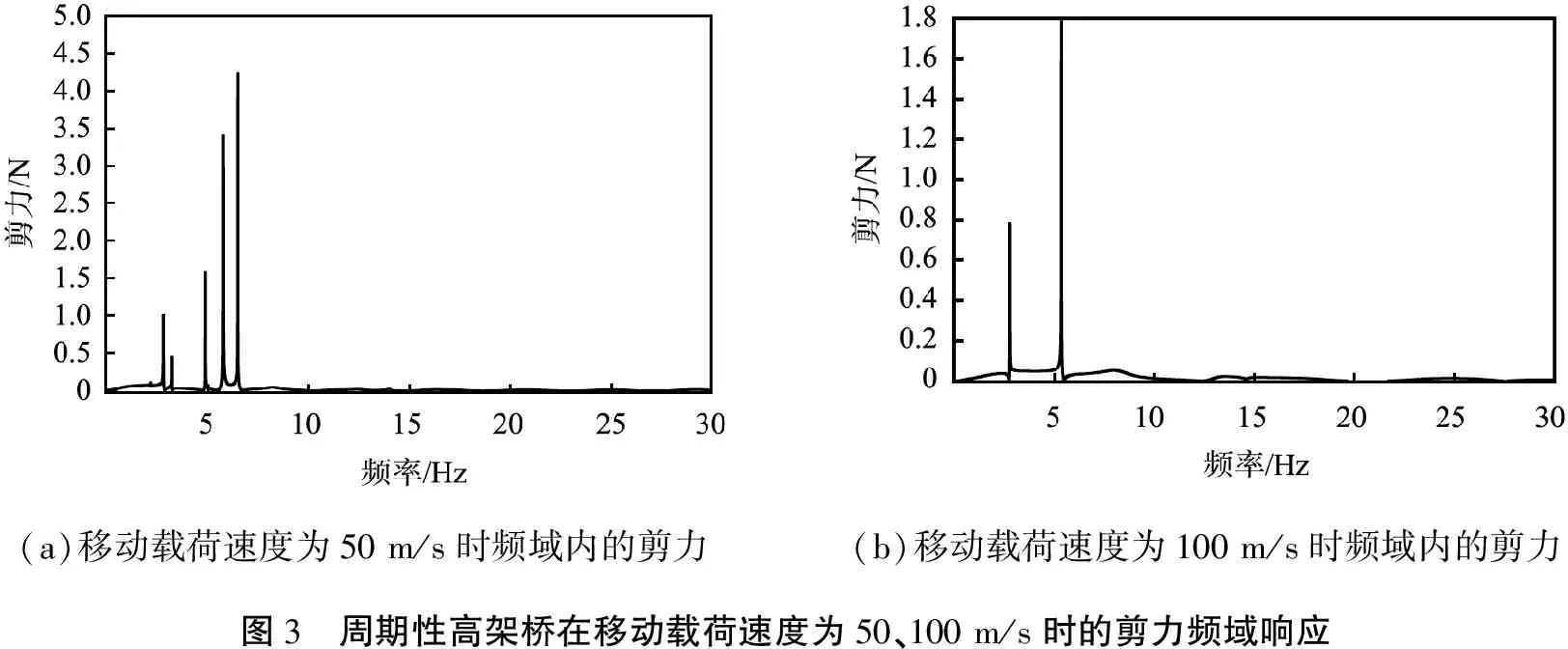
(a)移动载荷速度为50 m/s时频域内的剪力(b)移动载荷速度为100 m/s时频域内的剪力图3 周期性高架桥在移动载荷速度为50、100 m/s时的剪力频域响应
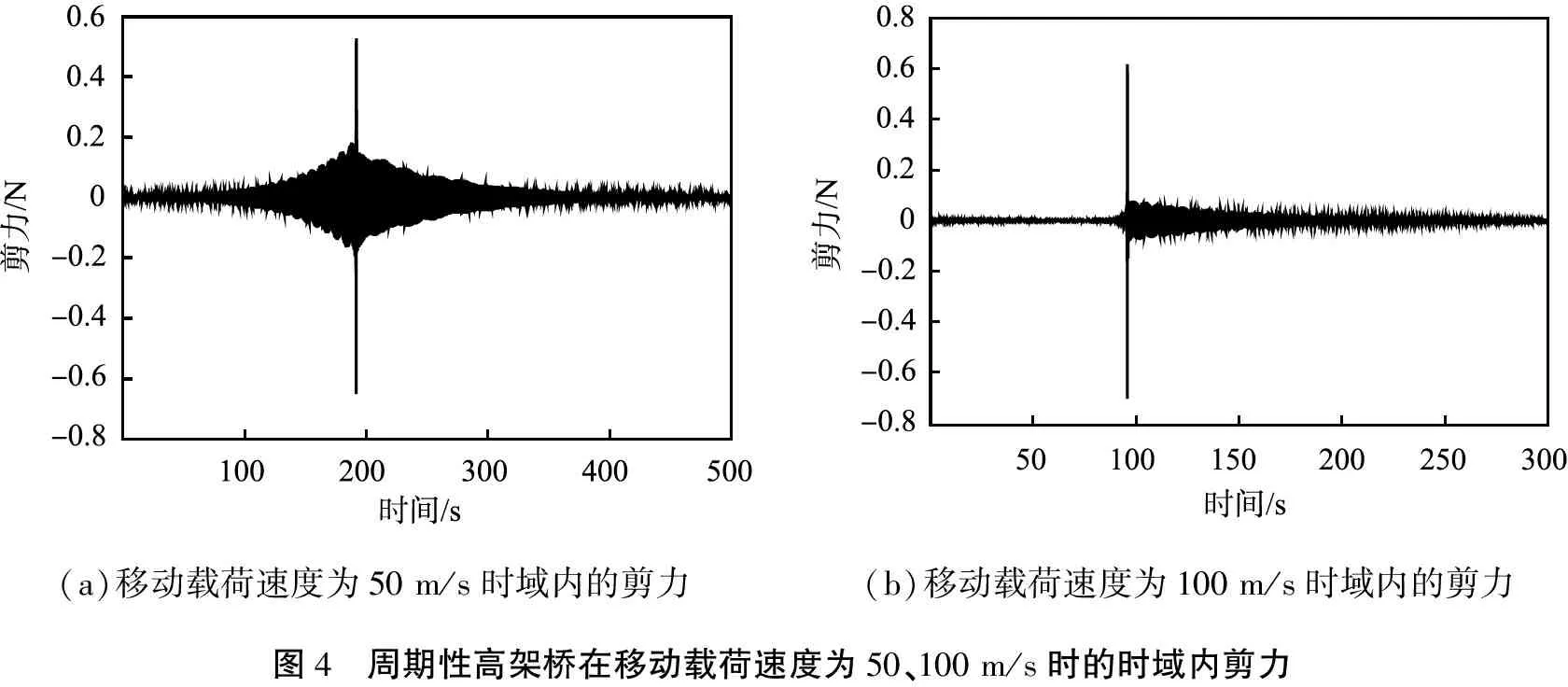
(a)移动载荷速度为50 m/s时域内的剪力(b)移动载荷速度为100 m/s时域内的剪力图4 周期性高架桥在移动载荷速度为50、100 m/s时的时域内剪力
5 结论
本文中提出了一种计算移动载荷作用下PV动力响应的有限元数值计算方法。采用Fourier变换将移动载荷作用下PV的动力响应问题转化为频率波数域内单位简谐荷载下PV的动力响应问题。考虑梁-梁-墩处的连接条件,建立了PV代表跨的有限元方程,利用Fourier逆变换求得PV在时域内的动力响应。计算结果与TM方法得出的结果进行对比,验证了本文中提出的模型。
1)移动荷载的速度会影响高架桥频域内响应的峰值个数,速度增加,峰值个数会减少;此外,随着载荷速度的增加,高架桥时域内的响应呈现类似冲击波特征。
2)从本文中的算例可以发现,有限元法和TM法在运用于均质等截面梁和墩时结果一致。实际上,有限元法比TM法有更好的适用性,还适用于非均质、非等截面的周期性高架桥。此外,该模型还可推广到考虑桩土相互作用的情形下,非均质的周期性高架桥对移动载荷的动力响应。
3)虽然本文中提出的有限元模型针对无限周期性高架桥,但在实际工程中,对跨数达到一定数量的有限周期性高架桥,也可应用此模型来近似地分析其对移动载荷的动力响应。

