基于最小二乘法的称重压力传感器的非线性拟合

，，

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

在轮式装载机动态称重装置中，物体的质量是通过压力传感器测得的压力值来间接表示的，通常压力传感器的输入与输出值是非线性的关系[1-2]。 动态称重所选用的压力传感器，输出特性明显呈曲线，如果用直线代替数据的输出，会产生较大的误差。 定义线性度的方法有很多，常用的有以下3种：

1)理论线性度，它是把原点与采集数据的最大值的点相连而成的直线；2)端基线性度，它是把数据的平均首末端相连作为参考的直线；3)最小二乘拟合[3]。

前2种方法由于忽略了中间数据量的影响，因此只取首尾作为参考。当数据在中间数据量波动较大时势必会对线性度产生较大的影响，造成误差增大，而最小二乘法是一种有效的拟合方法。最小二乘法拟合效果的好坏取决于线性函数所得的残差平方和的大小，残差平方和越小，拟合效果越好。

本文中选用非线性拟合方法，即最小二乘法来实现称重压力传感器的非线性拟合,介绍了2种计算最小二乘参数的方法,并分析其不确定度。

1 称重压力传感器的输出特性及拟合曲线

压力传感器属于高精度的传感器[4]，它的输出特性呈非线性。如果所得曲线越逼近压力传感器所采集到的实际数据，非线性误差就越小,这时就要进行曲线拟合。曲线拟合大致可以分为以下3个步骤：第1步，建立坐标轴，将所采集到的数据标注在坐标轴上，根据标注的点的图形来选择合适的数学模型；第2步，选择合适的数学模型中的待定参数；第3步，根据确定出的参数求出所选的数学模型。实际求出的模型参数与实际数据会存在误差，这时需要判断误差的大小及原因，误差越小说明该拟合曲线越接近实际测量值，这个误差的大小通常是用最小二乘法当中的残差平方和来表示。

对于压力传感器得到的液压数据，最小二乘法是实现该数据拟合的一种方法。通过某一个变量代换求解线性拟合直线来代替求解非线性拟合曲线，通过变量代换以后，所求解非线性曲线可以化为一元线性方程。

1.1 非线性曲线模型的确立

理论上载荷力与压力呈线性关系，实际测量的压力传感器的压力值与载荷力呈现如图1所示的实测曲线。可以看出，该曲线接近指数函数，将该曲线看作指数函数并作为一个数学模型，进行线性关系的拟合。假设曲线模型为

y=aebx,

(1)

式中：a为常数；b为自变量的系数；e为指数函数；x为自变量；y为因变量。

将式(1)等式两边同时取对数得

图1 载荷力与压力的函数关系图

lny=lna+bx,

(2)

式中：lna为常数；b为自变量系数；x为自变量；lny为因变量。

通过上述公式变换以后，指数函数就可以转化为一个自变量为X、因变量为Y的一元线性方程，

Y=A+BX，

(3)

式中：A为常数；B为自变量系数。

1.2 线性方程的拟合

压力的采集选用高温型压力传感器NY316T，4～20 mA恒流输出，量程0～12 MPa。将电流作为输出可以减少传输过程中信号的损耗。进行交流/直流转换之前需要串联一个电阻来实现电流到电压的转换，考虑到环境温度与油温会对阻值产生一定的影响，这里选用了高精度低温漂电阻RX70，阻值为500 Ω。

Y与X作为变量代换值，以标准砝码2 500 kg进行测试，并选择了20组数据，如表1所示。根据表中的数据，推导出一元线性方程中的参数A与B，求解A与B最常用也很有效的方法是最小二乘法。

(4)

(5)

式中：LXY表示先对X求偏导再对Y求偏导；LXX表示X求偏导后再对X求偏导。

把表1数据代入公式(4)、(5)，得A=0.078 6,B=0.017 3。

故该直线拟合方程可以表示为

Y=0.078 6+0.017 3X。

(6)

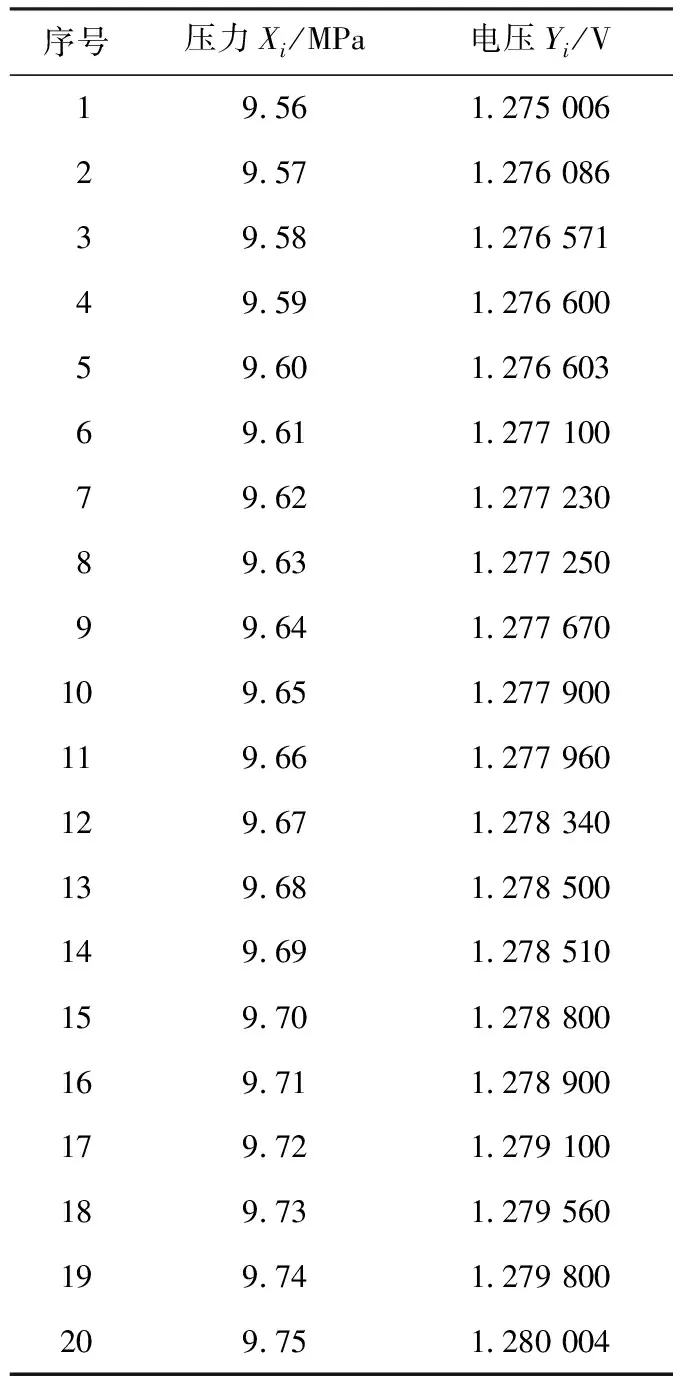
表1 压力传感器输出特性值与变量代换值

通过可视化数据分析软件origin将这20组数据导入并列出线性回归方程[5]，绘制出如图2所示的拟合曲线。图中黑色点为采集数据所对应的点，可以看出压力传感器的输入与输出特性呈现非线性关系，如果直接用直线方程拟合，得出来的结果误差较大，需要对数据进行非线性拟合，进而减小误差，提高称重精度。

图2 实验数据点的线性拟合直线

1.3 非线性方程的拟合

由于前面假设式(1)作为非线性模型，因此根据代换关系A=lna可得

a=eA，

(7)

式中：a为因变量；A为自变量。

代入A的值，a=eA=1.081 7，b=B=0.017 3。

将a与b的值代入式(1)，可得压力传感器的非线性拟合方程为

y=1.081 7 e0.017 3x。

(8)

在MATLAB中对该指数函数作图，如图3所示。该幂指数函数拟合后的非线性曲线更加接近称重压力传感器的实际输出。

图3 最小二乘法的非线性拟合曲线

2 最小二乘法参数的求解

这里介绍2种求解最小二乘参数的方法，通过MATLAB编程求解[6-7]。

2.1 求最值

假设采集到的数据的模型为线性方程y=kx+b，而实际所采集到的数据会在这条直线方程上下波动。当自变量x不变时，因变量y由直线方程计算所得，所得结果有一定残差，这个残差可以表示为

(9)

式中：P为残差；n为一元线性方程个数；yi为因变量；xi为自变量；k为自变量系数；b为常数。

最小二乘法就是求得使P为最小值时的k与b的值，把P看作是k与b的函数，即为高等数学中的多元函数求最值问题[8-9]，分别对式(9)中的k与b求导，可得

(10)

整理得

(11)

得到k与b的值为

(12)

该计算过程可在MATLAB环境下进行，通过polyfit函数实现[10-11]，具体过程如下：

x=[9.56,9.57,9.58,9.59,9.60,9.61,9.62,9.63,

9.64,9.65,9.66,9.67,9.68,9.69,9.70,9.71,

9.72,9.73,9.74,9.75]，

y=[0.242 950, 0.243 797, 0.244 177, 0.244 200,

0.244 202, 0.244 591, 0.244 693, 0.244 709,

0.245 038, 0.245 218, 0.245 265, 0.245 562,

0.245 687, 0.245 695, 0.245 922, 0.246 000,

0.246 156, 0.246 516, 0.246 703, 0.246 863]，

p=polyfit(x,y,1)，

x=0.017，y=0.078 6。

由于假设的拟合模型为线性的，因此该问题也可看作线性规划问题，通过将实验数据导入作图软件origin，绘制出图2的拟合直线，计算所得结果也为k=0.017 3，b=0.078 6。

2.2 矩阵形式

矩阵形式是另一种方法，可在MATLAB环境下运行，具体推算过程为

yi=a1xi+b1，i=1,2,…,n，

(13)

式中：a1代表一元线性方程自变量系数；b1为常数。

将式(13)改写成矩阵形式，

(14)

式中：

令X的转置矩阵与矩阵Y相乘可得

(15)

式中：XT代表矩阵X的转置矩阵；a、b代表矩阵的列向量。

(16)

3 不确定度分析

不确定度指的是标准数值波动范围。受环境温度的影响，压力传感器的测量值会存在一定的误差，为了更好地反映非线性拟合曲线的精确度的高低以及可靠性，对该曲线进行不确定度分析。

3.1 变量Y的残余标准差

(17)

式中Q表示变量Yi到拟合直线的残余误差的平方和。

此时Y的残余标准差S为

(18)

式中N为数值的个数。

3.2 非线性拟合曲线预测值的不确定度

在不确定度中通过残差平方和以及残余标准差来表示非线性拟合程度的好坏。残差指的是真实值和估计值之间的差值，残余标准差为残余平方和的开方，残余标准差越小则非线性拟合程度越好。

非线性拟合中，影响拟合曲线精确度的因素有2个，一是所选的函数模型，二是函数模型当中的残余平方和以及残余标准差的大小。

4 结论

本文中讨论了采用最小二乘法实现轮式装载机压力传感器液压值与称重货物之间非线性拟合的问题，具有一定的实际应用价值，结果表明非线性拟合后的曲线更加接近压力传感器的实际输出。给出2种最小二乘参数的计算方法，同时对非线性曲线的不确定度进行了分析，找到了影响拟合曲线精度高低的因素。