带有指令滤波的孤岛分布式能源系统反步控制

，，，，，

(1.南京工程学院 电力工程学院，江苏 南京 211167；2.江南大学 物联网工程学院，江苏 无锡 214122；3.国网宿迁供电公司，江苏 宿迁 223800)

近年来，分布式能源(distributed energy resource, DER)以其优良的经济性与环保性，越来越受到人们的关注，从而得到了快速发展[1-3]。利用孤岛DER系统可以解决一些偏远地区的用电问题，诸如远离陆地的海岛，由于离陆地较远，无法使用大电网进行供电，因此可利用海岛上丰富的风能或太阳能进行发电，并通过蓄电池及电力电子设备组建DER系统，对微电网或直接给负载供电，以满足区域内的用电需求[4-5]。距离的因素造成此类微电网无法与大电网互联，即运行在孤岛模式，而运行在孤岛模式下的微电网自身容量较低，自我调节能力欠缺，使得其在负载切换及负载产生扰动的情况下很难保持输出电压及频率的稳定，对用电设备及人身安全造成威胁[6]，因此本文中主要针对如何保证孤岛DER系统输出电压稳定展开研究。

对于DER系统的孤岛运行问题，一些学者已做了相关的研究。文献[7]中采用分布式能源增发与电容和负荷的投切控制，开发了孤岛自趋优化分布的智能体系统，对孤岛微电网的无功功率进行控制，从而保证了系统电压稳定，但仿真中只考虑了风速及光强变化时无功功率及母线电压的调节，未考虑负载产生扰动的情况。文献[8]中对传统主从控制进行了改进，提出了孤岛DER系统的耦合同步方法，验证了系统的稳定性，从理论上证明了方案的可行性，但研究同样没有考虑负载扰动的情况。当电网投入实际运行时，电网所接的负载会根据用户的需求随时处于变化状态，因此在对微电网输出电压进行控制及仿真时，考虑负载的变化能使仿真更贴近实际运行状态。文献[9]、[10]中采用Droop控制策略，使用了电气模型对孤岛DER系统切换负载及电源因故退出而切换电源这2种情况进行了仿真分析，结果显示系统的输出电压频率均得到了有效的控制。文献[11]中则采用分数阶滑模控制策略，对孤岛DER系统的输出电压进行控制，使输出电压有效地跟踪参考电压，并用电力系统计算机辅助设计(PSCAD)软件进行仿真验证，达到了很好的控制效果。

非线性系统是其状态变量和输出变量不满足叠加原理的系统[12]，对非线性系统的控制一直是国内外学者研究的热点。反步控制方法由美国学者Kokotvic等于1991年首次提出，主要思想为递归设计方法，通过系统降阶，并对每一层系统设计虚拟控制器，理论上能实现对n阶非线性系统的控制，有效地解决了高阶非线性系统的控制问题[13]，但是反步控制方法也具有自身的缺陷，如微分膨胀问题，可能会导致系统稳定性下降[14]。对此，本文中在使用反步控制方法的基础上加入指令滤波器，目的是解决反步控制方法中对虚拟控制量重复求导问题，减少了系统计算量。文献[15]中使用指令滤波反步控制方法对电液伺服系统进行了控制，解决了在外部扰动与输入饱和时轧机电液伺服系统的位置控制问题，避免了反步控制中的计算膨胀。文献[16]中则将指令滤波反步控制方法运用到背靠背直流输电系统中，有效地控制了有功与无功功率的协调与调度，并维持了直流输出电压的稳定。从众多的应用实例可以看出，带有指令滤波的反步控制策略能很好地对被控对象进行控制，并且解决了反步控制中计算膨胀问题。

本文中设计了带有指令滤波的反步控制器，应用在二阶孤岛DER系统的控制中，使系统输出电压在负载切换或参考电压突变的情况下实现对参考电压保持很好的追踪效果，从而达到不依靠末端电流而保持输出电压频率的稳定，并使用MATLAB/Simu-link仿真验证此控制器的控制效果。

1 孤岛DER系统结构

图1给出了孤岛DER系统结构图。从图中可以看出，孤岛DER系统包括了DER电源、电流支撑电容Cdc、三相桥式电压源换流器(voltage source converter, VSC)及电感电容(LC)滤波器，系统输出电压经变压器降压后给负载供电。电流支撑电容Cdc并联在VSC直流侧，意在过滤直流侧的电压波动，维持直流电压稳定平滑。图1中L与Cf分别代表LC滤波器的电感与电容，R表示滤波器及VSC中电阻损耗。三相变量vtabc、iabc、vsabc及isabc分别表示VSC末端电压、VSC交流侧电流、DER系统末端电压及VSC交流侧末端电流。在实际运行中，DER系统直流侧往往使用光伏阵列或风机提供持续的直流电，图1中则使用直流电压源代替光伏阵列或风机充当直流电源。

系统中各测量的三相变量经过派克(dq)变换后，送入控制器进行计算，系统的整个控制过程也在dq旋转坐标系下完成。控制过程中，先将控制器需要的三相电压、电流信号转换到dq旋转坐标系下，再将dq旋转坐标系下的信号输入控制器。在控制器中，dq旋转坐标下的电压、电流信号与参考电压信号vsdref、vsqref进行对比计算产生dq旋转坐标系下的控制信号mdq，并经过dq逆变换成三相坐标系下的控制信号mabc后，输入脉冲宽度调制(pulse width modulation, PWM)信号发生器。在PWM发生器中，三相控制信号与幅值为1的三角波进行对比产生高低电平，并经取反叠加产生6路脉冲信号输入VSC，完成控制过程，实现输出电压对参考电压的跟踪。由于本文中DER系统不与大电网互联，即运行在孤岛模式，无法使用锁相环(phase locked loop, PLL)对DER系统的频率与相位与大电网进行锁定[17]，因此本文中将人为设定固定的系统角频率，输入压控振荡器(voltage controlled oscillator, VCO)得到旋转角ρ后，提供给dq变换器使用。

L与Cf分别代表LC滤波器的电感与电容；R表示滤波器及VSC中电阻损耗；三相变量vtabc、iabc、vsabc及isabc分别表示VSC末端电压、VSC交流侧电流、DER系统末端电压及VSC交流侧末端电流。图1 孤岛分布式能源(DER)系统结构图

2 孤岛DER系统数学模型

利用Kirchhoff电压及电流定律对图1孤岛DER系统进行数学建模，系统中电压与电流分别有如下关系式：

(1)

(2)

(3)

(4)

将式(4)中各空间向量转换到dq旋转坐标系下，可得到如下表达形式：

(5)

(6)

(7)

3 指令滤波反步控制器设计

本节主要利用反步控制方法，针对上述模型，对d轴与q轴分别设计了反步控制器，并将指令滤波器加入反步控制器的虚拟控制器中，避免了对虚拟控制器的反复求导，使输出电压能够快速跟踪参考电压。

步骤1d轴控制器设计，为使系统降阶，定义

(8)

式(8)中fd(vsd,vsq,isd,isq)与g分别表示为

(9)

(10)

定义追踪误差

e1=vsd-vsdref，

(11)

(12)

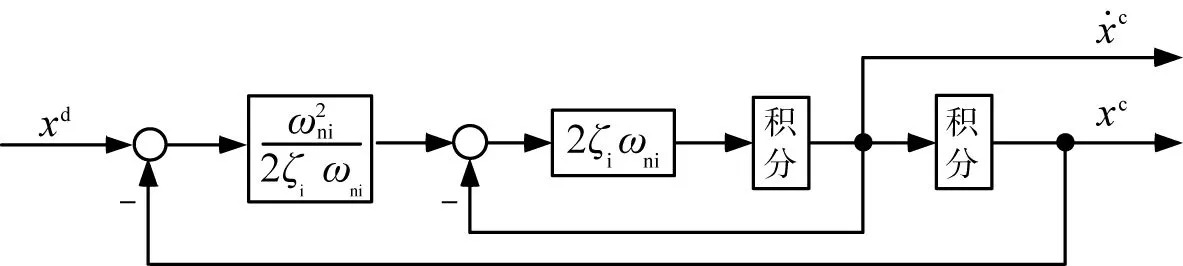
xd为指令滤波器输入信号；xc为指令滤波器输出信号；为指令滤波器输出信号的微分；ζi、ωni 分别表示指令滤波器的阻尼与带宽。图2 指令滤波器结构

根据式(11)(12)，得到追踪误差导数为

(13)

(14)

为了稳定式(13)，定义Lyapunov函数为

(15)

对式(15)求导并将式(13)代入，得到

(16)

式中k1为大于零的常数，此时若设计虚拟控制器为

(17)

(18)

(19)

为了补偿指令滤波器的滤波误差，重新定义误差量为

(20)

式中ε1为指令滤波器的误差补偿信号，设计为

(21)

为了稳定式(14)，再次定义Lyapunov函数为

(22)

对式(22)求导可得

(23)

(24)

将式(14)(24)代入式(23)可以得到

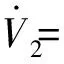
(25)

为满足Lyapunov稳定性定理，设计d轴控制器为

(26)

式中k2为正常数。

步骤2 使用同样方法对q轴设计控制器，进行如下定义：

(27)

式(27)中g与式(10)定义相同，fq(vsd,vsq,isd,isq)定义为

(28)

定义追踪误差为

e3=vsq-vsqref，

(29)

(30)

(31)

(32)

为了稳定式(31)，定义Lyapunov函数为

(33)

对式(33)求导并将式(31)代入得

(34)

式中k3为大于零的常数，根据d轴控制器设计的经验，此时设计虚拟控制器为

(35)

与d轴控制器类似，在q轴控制器设计过程中引入指令滤波器，重新定义误差量为

(36)

式中误差补偿信号ε2设计为

(37)

为了稳定式(32)，定义Lyapunov函数并求导，得

(38)

(39)

将式(36)求导并将式(31)(35)(37)代入得到

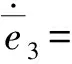
(40)

将式(32)(40)代入式(39)得

(41)

同样，为了满足Lyapunov稳定性定理，设计q轴控制器为

(42)

式中k4为正常数。

所设计控制器的控制流程如图3所示。

4 稳定性分析

在本文第三节中对系统输出电压d轴与q轴分别设计了控制器进行控制。在d轴控制器的设计过程中，使用了2次Lyapunov函数来保持稳定性，分别为式(15)与式(22)。观察式(15)与式(22)可以得到，V1与V2均恒大于等于零。

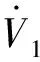
vsd、vsq分别为系统输出的d轴和q轴电压；vsdref、vsqref分别为d轴与q轴参考电压；分别为d轴和q轴虚拟控制器；ε1、ε2分别为d轴和q轴中指令滤波器的滤波误差；分别为d轴和q轴中指令滤波器的输出信号；md、mq分别为所设计的d轴与q轴控制器；ω为系统参考频率；ρ为系统旋转角；为调制波。图3 指令滤波反步控制流程

(43)

总结以上结论，可以得到如下公式：

(44)

(45)

(46)

(47)

根据Lyapunov稳定性理论可以得到d轴控制器在原点处渐进稳定。同理，可以证明q轴控制器在原点处也处于渐进稳定，从而保证了整个系统的稳定性。

5 仿真及结果分析

本节通过MATLAB/Simulink仿真对本文中所设计的指令滤波反步控制器的控制效果进行验证。仿真使用电气模型，其仿真结果中存在谐波，较数学模型能更真实地模拟实际运行情况并且反映运行中出现的问题。 表1给出了电气仿真模型中各元件的参数及单位。 在仿真过程中，将给系统输入电压参考信号，并在参考信号中设置了阶跃信号，同时给系统设定了三相平衡及不平衡2种负载，以观察在各种扰动情况下控制器的控制效果及输出电压对参考信号的跟踪效果。 表2给出了2种负载的具体参数。 在仿真过程中，对控制器参数k1—k4进行了调节，以保证仿真具有良好的输出效果，最终选择控制器参数k1=3 500,k2=13 000,k3=4 500,k4=12 000。

表1 分布式能源系统元件参数

表2 不同类型负载参数

整个仿真过程持续2 s，当0≤t≤0.05 s时，d轴参考电压vsdref从0 V线性上升至450 V，随后在450 V维持稳定；当t=1.5 s时参考电压从450 V突变至520 V，随后一直稳定在520 V直至仿真结束。q轴参考电压vsqref则一直保持0 V不变。在仿真开始时，系统负载侧接入三相平衡负载，t=1 s时，三相平衡负载切出系统，当t=1.007 s时三相不平衡负载接入。图4显示了整个仿真过程中dq旋转坐标系下系统输出电压与对参考电压的跟踪情况。可以看出，在仿真的整个过程中，系统的输出电压始终对参考电压保持跟踪，当参考电压产生阶跃信号时系统输出电压能快速恢复跟踪，且未产生较大的超调。从图4的放大图中可以看出，当负载从三相平衡负载切换到三相不平衡负载时，系统输出电压一直维持稳定，并未因为负载切换而产生波动。

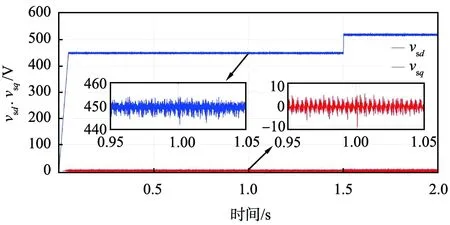
图4 dq旋转坐标下系统输出电压

图5给出了系统在0.9～1.1 s之间输出电压与电流的放大图。从图中可以看出，负载切换导致输出电流波形发生改变，但是电流的改变并未对系统输出电压造成影响，系统输出电压依然保持在稳定状态，说明所设计的控制器达到了预期控制效果。

(a)系统输出三相电压

(b)系统输出三相电流图5 0.9～1.1 s时系统输出电压与电流

图6给出了1.6～2 s时系统输出电压最终稳定时电压的谐波分析。从图中可以看出系统各谐波与基波幅值比均维持在0.07%以内，电压谐波总畸变率为0.64%，满足所期望的电能质量要求。

图6 1.6～2 s时系统输出电压的谐波分析

6 结语

本文中围绕孤岛DER系统输出电压的稳定问题展开研究，根据系统的数学模型设计了反步控制器，而后加入了指令滤波器，避免了传统反步控制中对虚拟控制器的反复求导，消除了反步计算中的微分膨胀问题，通过稳定性分析验证了控制器满足Lyapunov稳定条件。在参考电压突变及负载变化的情况下对系统进行了仿真，结果表明，输出电压对参考电压在所给情况下均能保持很好的跟踪效果，验证了所设计控制器的控制效果。对输出电压进行了谐波分析，验证了输出电压能够满足电能质量要求。