分类讨论在初中数学教学中的应用

单兰花

（苏州工业园区第十中学，江苏苏州 215021）

分类思想主要是将研究对象合理分类，并进行相应的分析讨论，再归纳得出结果。分类讨论是深入研究问题较常用的手段，需要人们在实践中了解、掌握解答问题的思路和技巧。在数学教学过程中，分类讨论方法的运用范围相对广泛，如有理数、不等式、绝对值、圆的位置关系、等腰三角形、图形位置关系、含字母的方程等。本文主要对分类讨论思想在初中数学教学中的应用进行分析。

一、分类讨论在坐标与图形中的应用

分类讨论思想在坐标和图形中的应用较多，教学的重点通常集中于坐标系中各种图形的变化方式，并将坐标与三角形、双曲线、矩形以及抛物线等结合。同时，将分类讨论的方法应用于坐标图中，有助于题目灵活变换，并能有效培养学生的想象力。

例1：在平面直角坐标系中，O为坐标原点，点A的坐标为，点M为坐标轴上的点，并且△MOA是等腰三角形，则满足相应条件的点M有多少个？

本例题主要考查等腰三角形的判定、图形性质、坐标、分类讨论以及数形结合等数学知识。分别以O、A为圆心，以OA长为半径作圆，与坐标轴交点即为所求点M，再作线段OA的垂直平分线，与坐标轴的交点也是所求的点M，作出图形。采用图形分析，得出结论为6个。见图1。

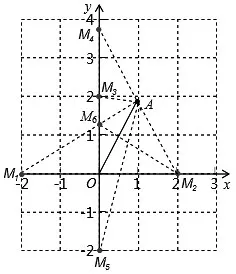
图1

例2：如图2，在平面直角坐标系中，O为坐标原点，矩形OABC的A、C坐标分别为（10，0）、（0，4），OA的中点为点D，点P在BC上可移动，当△ODP为腰长为5的等腰三角形时，点P应该在哪个位置？

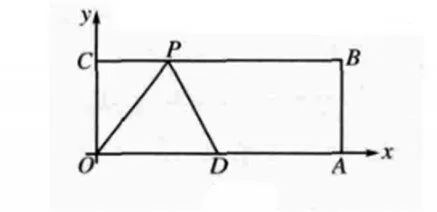
图2

本例题主要考查坐标与等腰三角形的性质、图形的性质以及勾股定理等知识，并且需要应用到分类讨论来对题目问题进行解答。点P属于不确定点，应用等腰三角形的性质分三种情况来讨论，再采用勾股定理便可解出P点的坐标。△ODP的腰长为5，可有3种情况：当P点在D点的左边时，若PD=OD=5，得出点P的坐标为（2，4）；若OP=OD=5，P点的坐标为（3，4）；当P点在D点的右侧时，PD=OD=5，P点的坐标为（8，4）。

二、分类讨论在等腰三角形中的应用

涉及等腰三角形的问题经常需要分类讨论，并且中考出现的概率相对较高。该类型题目通常会出现三角形腰长与其底边长的比较，或顶角与底角的比较等。相对复杂的等腰三角形问题，主要结合圆形或者坐标等知识来综合考查。而由于综合题目具有一定的难度，学生需要掌握等腰三角形的性质以及核心内容。

例3：已知（a-1）2+∣b-2∣=0，a、b为等腰三角形的边长，此等腰三角形的周长应为多少？

本例题主要考查偶次方、绝对值以及三角形的性质，难点在于解题的思路。应用分类讨论来分析问题的结果，并且进行相应的说明，更有助于学生理解。首先根据平方、绝对值可计算出a、b，即a=1，b=2，再根据三角形三条边之间的联系，即两边之和大于第三条边，两边之差小于第三条边，即得出此等腰三角形的腰为2，底为1，周长为5。

例4：已知等腰三角形的一个角为80°，求此等腰三角形的顶角度数。

本例题主要对等腰三角形的底角度数相等、三角形的基本性质等进行考查，运用定理：三角形内角和等于180°，即可解答问题。此等腰三角形的顶角可直接为80°。当三角形的底角为80°时，其顶角应为180°-80°×2=20°。由此可知，此等腰三角形的顶角可为80°，也可为20°。

三、分类讨论在动点型题目中的应用

动点型分类讨论题是中考题中常出现的压轴题，同时也是难度相对较大的题目。想要解决此类大题，学生需要了解数学基础知识，并熟悉、掌握、运用坐标、三角形、圆形以及运动理论等相关知识。同时，还需先寻找出问题的关键词，掌握题目的变化量以及运动要素，以便更好地解决问题。

例5：射线QN和△ABC的两条边AB、BC相交于M、N，并且AC//QN，AM=MB=2cm，且QM=4cm。动点P从Q点出发，沿着射线QN以1cm/s的速度向右边移动，t秒之后，以点P为圆心，以 3cm为半径的圆形与△ABC相切，两图形的切点在其边上，求出t可选择的一切值。

应该结合等边三角形的性质、切线的性质来对题目进行解答。题目中已知△ABC为等腰三角形，并且AM=MB=2cm，点P从Q点出发，沿着射线QN以1cm/s的速度向右边移动，会出现3种切线情况。利用切线的性质、直角三角形的勾股定理、等边三角形基础知识，以及速度、时间、路程之间的关系进行解题，即可得出t=2，t=3和t=7，t=8；随后，对其进行分类讨论分析，便可得出答案为t=2或7≥t≥3或t=8。

本例题主要考查等边三角形的性质、直角三角形的性质、勾股定理以及切线的性质等知识。在解答题目的过程中，需要注意对题目进行分类讨论和分析，并对得出的结果进行总结和归纳，且在计算出结果之后，需要再一次对结果进行验证，以保证答案的准确性。

四、分类讨论在图形拼接中的应用

在对几何图形进行拼接的过程中，需要合理应用分类讨论方法，必须注意拼接的合理性，即需要从问题的角度以及已知的长度方面来进行配合，不能够任意拼接；同时，需要仔细观察拼接后得出的图形，然后对拼接前的切线进行合理的规划。

例6：一张含一个30°角，并且最小边长为2的直角三角形纸，沿着图片中的中位线剪开后，再将两个小纸片拼接为一个平行四边形，拼接得出的平行四边形周长为多少？

运用三角函数可得出BC=4，AC=23，再通过中位线的性质得出AD=CD=3，BF=CF=2，DF=1，随后再进行拼图，可得出图3显示的结果，即一个可拼接成矩形，一个可拼接成平行四边形，随后即可计算出拼接图形的周长，其周长为8或4+23。

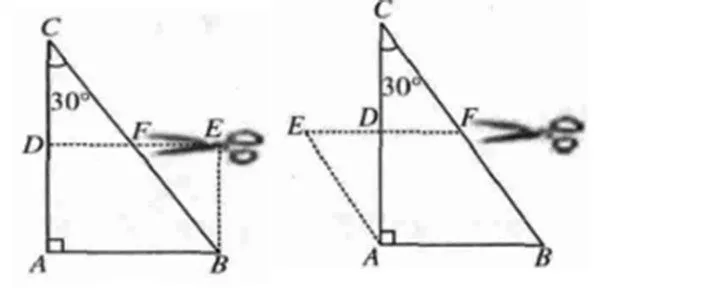
图3

本例题主要考查图形的拼接，其解答的关键就是根据题目要求来画出需要的图形，然后再对题目进行全面的考虑。对题目进行分类讨论的同时，合理采用数形结合的方法，有助于快速而正确地对题目进行全面的总结和归纳，从而有利于快速得出正确的计算结果。

总之，分类讨论思想在数学教学过程中使用的频率相对较高，在解答问题时，需要深入理解，掌握问题的本质，并对解题的思想和方法进行相应的研究，从而才能发现数学中的不同点和相同点，也才能对数学题目进行分类研究。注意，在分析的过程中，需要做到不重复、不遗漏，对于问题要学会进行合理、科学的分析，然后将计算得出的结果进行分类总结，并对得出的答案进行验证。