工业点源COD超标排放预警的估计方法

张 震,宋国君,刘 刚,王军霞

（1.中国环境监测总站,北京100012；2.中国人民大学a.环境学院；b.信息学院，北京100872）

0 引言

2015年7月，国务院《生态环境监测网络建设方案》印发，强调了监测与监管协同联动，尤其指出重点排污单位必须落实污染排放自行监测及信息公开的法定责任，政府要加强污染源监督性监测和监管。目前，污染源数量众多、监测任务繁重与政府监督性监测能力存在一定矛盾[1]，推行企业自行监测，依靠社会监测和公众监督，而由政府进行污染源监测质量管理控制将是未来趋势[2]。在线监测数据审核与监督性监测将成为污染源监督性监测的主要职能，虽然目前还存在监测频次及达标判据缺乏统一规定[3]、监测数据没有有效发挥应有的稽查作用[4]、污染源监测信息公开不足[5]等问题，但对于重点污染源监测与管理能力已经有了显著提高[6]。然而更为薄弱的是，针对没有安装污染物在线监测设施的非重点点源或小点源，以及重点点源无法使用在线监测设施测量的污染物，如重金属等，监督性监测的工作量仍非常繁重。而如果能够通过小样本排放监测，在一定置信区间内反映污染物排放状况，则能够大大降低污染源监测与管理难度。

本文借鉴美国水污染物排放许可证制定过程中，基于污染物排放统计分布规律用有限的数据估计排放的超标最大浓度的方法，并根据我国工业点源水污染物排放监测需要进行工业点源水污染物超标排放预警估计方法研究。

1 美国工业点源水污染物超标排放预警估计的统计方法

在美国排污许可证申请过程中，一旦污染物受纳水体的指定用途和水质基准确定，许可证签发机构必须确定排放是否会导致或者有潜在的可能性导致超过水质基准的定量和描述性限值[7]。如果超标，许可证签发机构必须确定相应的污染物排放限值来控制污染。在许可证制定初期，所获取的污染源排放的数据资料是非常有限的，必须借助小样本的监测数据收集来代表总体制定基于水质的排放限值[8]。本文所借鉴的方法就来源于此，主要是通过有限样本推断总体的99%分位数值，从而确定是否存在潜在的可能性超出排放标准。该方法计算方法与原理如下：

污染源水污染物排放监测数据一般符合对数正态分布[9]。该统计方法的思想主要有两个方面，首先是基于需要的置信水平确定一个最高排放浓度所对应的百分位数：Pn=(1-置信度)1n，Pn是代表数据中最大浓度的百分位数，n为样本容量。对于Pn是代表数据中最大浓度的百分位数，n为样本的容量。

其次，确定存在的百分位数和对数正态分布上限之间的关系。例如，如果5个样本数据被收集到，变异系数为0.6（当N＜10时，美国环境保护署统一假定CV=0.6），对于需要的排放分布上限为99%，则两个百分位数可以通过之前提到的变异系数找到两者之间的关系：

对应的比值是期望值：

而2.326σ，-0.258σ两个值应该分别是对应在确定的分布情况下99%和40%百分位数点的临界值，用临界值代表不同的μ，从而确定两个期望值之间的比值。

最后，确定样本中五个数据中的最大值，乘以比值能够估计出在99%的临界点上的估计最大值。这个算法可以被用来对同一受纳水体范围内的单一或多个排污口进行反复测度。

2 工业点源COD超标排放预警估计方法改进

2.1 案例检验

通过以某市钢铁厂某年全年的在线监测COD数据为例进行检验。因为本方法为小样本的连续抽测，所以通过全年的连续监测数据进行模拟情景的分析。

首先随机产生全年中的每一天，选择当天以及前后两天共三天的数据，本文随机选取了2月8日、2月9日、2月10日三天的数据，根据对数正态分布的性质，将72组数据进行正态转化。使用SPSS V17.0进行K-S检验，符合对数正态分布特性。

其次，根据选择的时段，在三天72个样本中随机选取5组数据，为模拟样本选择的情景，随机抽取在线监测数据中某个时点的数据值，并且选取包括该数据的向下5个连续样本值。选取的结果见表1所示。

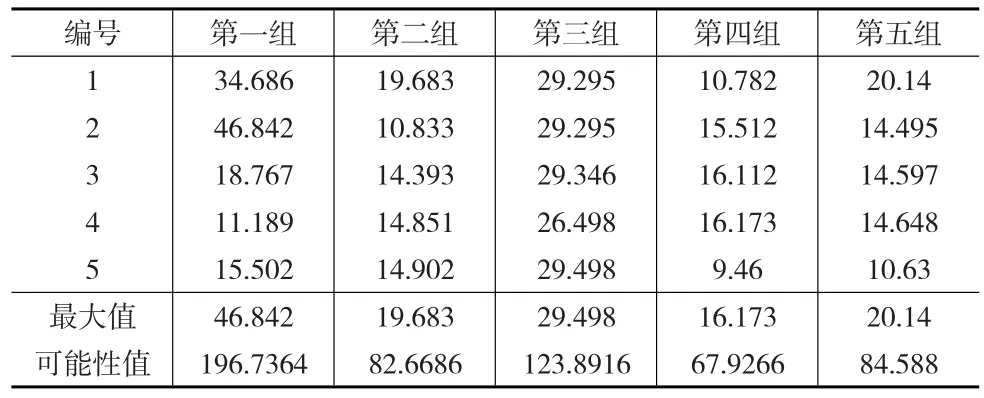
表1 样本选取结果（mg/L）

根据美国EPA方法，选择99%的置信区间，进行计算，假设没有水流稀释作用，则排放的污染物最高可达到196.7364mg/L，所依据钢铁行业的排放标准为100 mg/L，则其中有两组数据都显示具有潜在的可能性超标。但是在实际中，三天前后共一个月的时间内达标率为100%，如果按照该组数据作为监督性监测的应用，则与事实不符。

同样在此基础上，为进一步验证方法的准确性和改进的必要性对全年的数据随机选取5个日期时间段，对每个时间段进行同样五次随机抽取（结果如表2）。可见，在日期抽样组（C）中抽到超标值，去除超标值的最大可能性浓度为252.49mg/L，甚至超过该厂污水处理设施进水浓度标准，说明不合理的极端现象的确存在。注：表2中日期抽样组（C）中的第三组数据本身存在超标，因此不符合方法的应用条件且在实际不具有解释意义。这是因为如果样本值偶然靠近99%百分位数的临界点，则计算后的数值甚至可能高于进水浓度，导致结论荒谬，使所得结果不具有任何解释意义。

在这5次日期抽测数据中EPA的方法均有潜在的可能性超标出现，而实际数据中并不存在超标。但同时值得肯定的是，在C组抽样中，本身抽到了一次超标数据，而抽到的观测值潜在性超标高达四组，在出现前后也同样出现在线数据连续超标的情况（见表2）。因此，该方法在统计计算应用中存在偏差。

2.2 统计方法缺陷识别与改进

导致问题的根本是两个分位数所代表的期望的比值假定。依然假设为5个样本观测值，则可以得到：

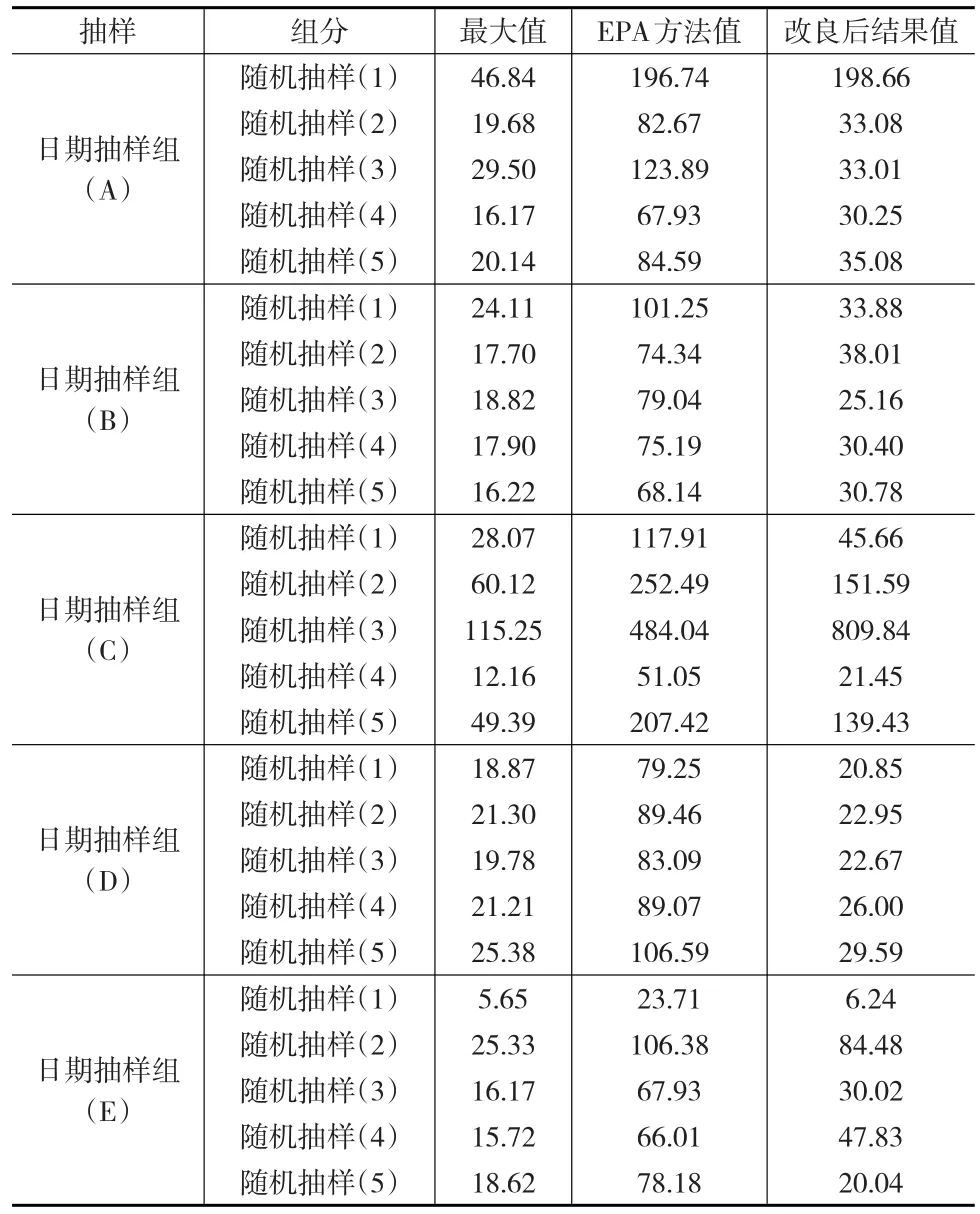
表2 五组25次抽样样本结果（mg/L）

其中σ是通过σ2=ln(1+CV2)公式得出，EPA固定的认为当n≤10，则CV=0.6，如果n＞10，则CV为样本标准差与样本均值的比值。

从统计学的角度，对σ的估计是不合理的。虽然通过σ2=ln(1+CV2)公式估计 σ2是正确的，但是作为 σ的估计并非无偏估计[10,11]，尤其是在小样本的情况下，估计的效率很低。正是因为这个问题，导致在实际的操作中σ的夸大，这就是为什么会导致出现高概率谬误的原因。

因此，只要找到能够对σ进行无偏估计的更好方法就能够解决其存在的缺陷。为解决其无偏性，本文对监测到的所有数据构建ln函数，转换为正态分布，计算SY，根据SY估计̂。这样就应用了所有监测的数据，而不是仅取用最大值；同时避免了EPA方法中当N＜10时，CV=0.6的武断做法，改进方法的统计步骤如下：

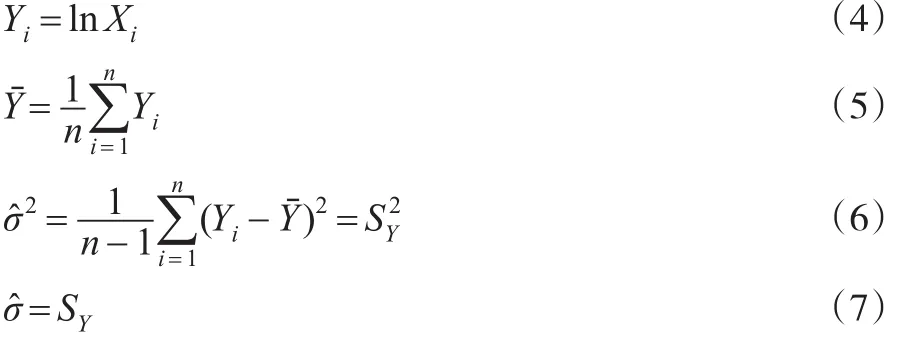
3 工业点源COD超标排放预警估计可行性分析

3.1 方法可行性分析

利用改良后的方法对抽测数据进行重新处理，结果见表2所示。在数据结果方面，直观对比5次日期随机选择，以及在相应的数据组中进行的5次随机选择得到的125个数据的分析结果，明显可以看出，EPA方法在日期抽样组中的超标率为100%，而事实上，达标率较高，只不过偶尔会有峰值出现，但是峰值也没有超过排放标准的要求。对比改良后的结果可以看出统计推断的潜在可能性超标率减小，但同时并没有影响到对超标情况所做出的预测。

3.2 案例验证

为验证针对工业点源水污染物超标排放预警估计方法的可行性，采用不同行业企业COD连续监测和手工监测数据进行分析验证，分别为B市某钢铁厂、某啤酒厂，J市某染织厂COD连续自动监测数据，J市某制药厂某时段手工监测数据。为模拟超标排放预警估计，选择上述企业存在超标或在超标临界点附近的连续数据，每个企业选择某时段9个连续监测浓度点，组成滑动五组数据，所用监测数据均是从年度连续监测数据中具有针对性的选择对应验证时段类型，从而验证在实际工作中连续核算的预警效果，核算结果见表3所示。

表3 工业点源水污染物超标排放预警估计案例验证（mg/L）

B市某钢铁厂提供了一个浓度点在排放标准临界点以下，未超标案例。连续9个小时内的变化趋势如图1所示。分组1预警值保持显示为低值，当出现浓度升高趋势时，分组2预警值开始显示超标，在下一个时段出现98.62 mg/L的排放标准临界值，则预警值明显升高，对工业点源污染控制设备管理和生产负责人员起到提醒作用。

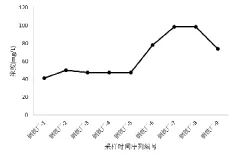
图1 B市某钢铁厂案例采样时段COD浓度变化趋势

B市啤酒厂案例提供了当污染物排放浓度出现突然变化的案例。在前7个时段，啤酒厂排放浓度保持在低值，当出现瞬间高值时，预警值反映为307.95 mg/L，在实际操作中若将预警值和标准值的的相对偏差设置不同预警层级，那么可以设置这种情况为高预警级别。（见图2）

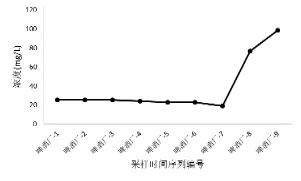
图2 B市某啤酒厂案例采样时段COD浓度变化趋势

J市某织染厂提供了在排放标准临界值之上的超标案例。最大值超出标准的范围不是很大，预警值的浓度出现实际超标。（见图3）

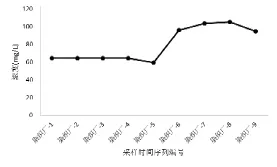
图3J市某染织厂案例采样时段COD浓度变化趋势

J市某制药厂提供了达超标，但是存在数据波动的情况。从预警值来看，主要出现在排放标准临界值附近，能够实现预警作用。因为该值为小时的手工采样值，可见手工采样与连续自动监测都能够使用该方法。（见图4）

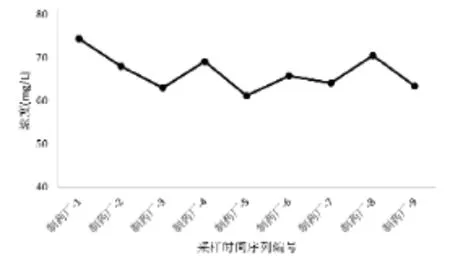
图4J市某制药厂案例采样时段COD浓度变化趋势

4 结束语

本文以工业点源水污染物超标排放预警估计的统计学方法研究为目的，针对美国NPDES之排污许可证中统计学思路为基础进行了改良应用，改善效果明显，能够发现潜在可能性的超标情况，目前的统计方法可以应用到以下几个方面：

（1）在监督性监测中通过小样本数据应用统计的方法估计总体排污状况，可以作为预防污染物排放超标，甚至是预防环境污染突发事件的重要依据，能够保证监督性监测和环境执法的科学有效性。

（2）利用有限的监督性监测样本发现潜在超标的可能性，则可以有针对性的增加对污染源抽查监测的频次，提供了加密抽查监测的依据，减少了出勤的次数，降低监督执法的人力物力成本。

（3）该方法同样适用于污染源的环境守法自测，由于其能够简便、及时的发现潜在超标可能性，从而帮助污染源发现生产和污水处理上的管理、技术漏洞，及时采取弥补措施，阻止环境违法行为的产生。