中国季度GDP初步核算数据质量的评估

杨利雄，张春丽

（1.兰州大学 管理学院，兰州 730000；2.西北民族大学 经济学院，兰州 730030）

0 引言

评估GDP初步核算数据是否能反映真实经济运行现状对战略决策和政策制定具有十分重要的意义。然而，宏观经济数据使用者常常面临及时性和准确性之间的权衡。由于修正数据难以满足及时性需求，为了及时地做出科学的决策，决策者所使用数据通常只能是初步核算数据。因此，数据使用者需要评估初步核算数据的质量。

初步核算数据可视为真实GDP数据的一个预测，分析初步核算数据与真实数据之间的统计关系，可以判断初步核算数据的质量。文献中常常使用有效性和无偏性检验来考察初步核算数据的质量[1，2]。因真实GDP数据无法获得，这些文献通常将最终核实数据视为真实GDP数据，从而评估初步核算数据相对于最终核实数据的无偏性和有效性。由于最终核实数据利用了更完善的基础资料，因而更接近真实数据，但其本质上依然是真实GDP的预测。如果初步核算数据与最终核实数据同时受到某种系统性影响，那么初步核算数据与最终核实数据可能会在某一时刻同时系统地偏离真实值，进而分析初步核算数据与最终核实数据两者之间的关系判断初步核算数据的质量，可能得到误导性结论。

本文基于组合预测理论、无偏性和有效性检验及时域-频域上的匹配分析，提出了一个评估初步核算数据质量的框架。将初步核算数据、初步核实数据和最终核实数据都视为是对真实GDP数据的预测，且假设真实GDP是不可观测的变量，因而真实的预测误差也是不可观测的。很多情况下，各种预测的简单平均就能显著地促进预测的精度[3]，组合预测的精度胜于单个预测[4—6]。因此，基于组合预测评估初步核算数据的质量具有优势。最优组合预测的权重依赖于初步核算数据、初步核实数据和最终核实数据的预测误差的方差和协方差。本文建立了预测误差的方差和协方差的估计方法，进而可以得到真实GDP数据的最优组合预测。在此基础上，考察初步核算数据与最优组合预测之间的关系，即无偏性和有效性；在时域-频域上对比初步核算数据、最优组合预测与美国GDP数据的匹配性，借此考察初步核算数据能否反映真实的经济运行现状。

1 模型与方法

1.1 最优组合预测

本文将初步核算数据、初步核实数据和最终核实数据都视为是对真实GDP的预测，且假设真实GDP是不可观测的变量。在此设定之上，探讨我国季度GDP初步核算数据的优良性。考虑组合预测：

其中 λ1，λ2∈[0，1]；GDPP、GDPF和 GDPS分别代表初步核算数据、初步核实数据和最终核实数据。预测误差满足：

其中eC=GDP-GDPC，eP=GDP-GDPP，eF=GDP-GDPF，eS=GDP-GDPS。GDP为真实国内生产总值数据。最优组合预测的权重可以通过最小化预测的均方误（MSE）得到：

其 中 σPF=cov(eP，eF)，σPS=cov(eP，eS)，σFS=cov(eF，

对式（3）关于λ1和λ2求导，得到最优权重：

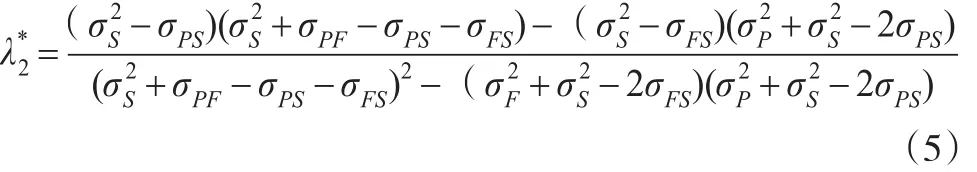
式（4）和式（5）表明最优权重是各预测方差及预测误差间的协方差的函数。根据前文对预测误差的定义，有：

进一步可得：

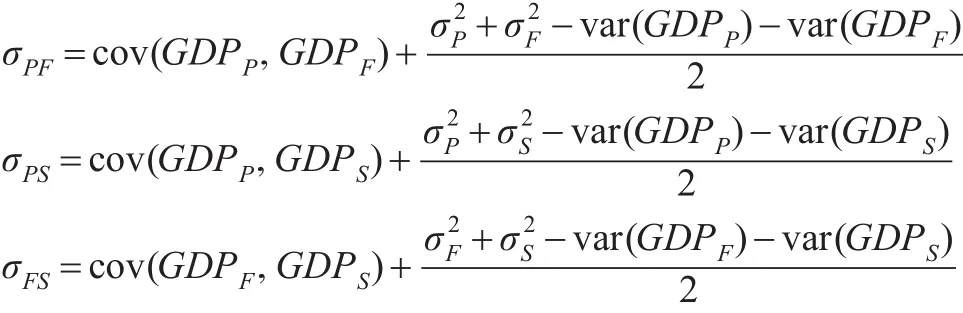
另一方面：

所以得到：

式（6）至式（11）的右边各部分可使用历史数据估计。即，各预测误差的方差估计和协方差的估计可以通过计算cov(GDPP，GDPF)、cov(GDPP，GDPS)、cov(GDPF，GDPS)、var(GDPF-GDPP)、var(GDPS-GDPP)、var(GDPS-GDPF)、var(GDPP)、var(GDPF)和var(GDPS)得到①本文使用Dicker-Fuller和Phillips-Perron单位根检验均发现我国GDP数据（包括初步核算数据、初步核实数据和最终核实数据）是含时间趋势的平稳序列；考虑时间序列存在结构突变的可能，使用Enders和Lee（2012）的单位根检验同样证实了GDP数据是平稳序列的结论。因而，初步核算数据、初步核实数据和最终核实数据的方差、协方差是可以计算的。。将上述各部分带入式（4）和式（5）得到最优权重的估计。

1.2 数据质量检验

基于上述最优组合预测，考察我国季度GDP数据的质量，检验季度GDP初步核算数据的无偏性和有效性。Mankiw和Shapiro（1986）[7]基于回归建立了检验数据有效性的方法，即考虑如下回归：

其中GDPCt为真实GDP的最优组合预测，GDPPt为GDP初步核算数据。通过检验原假设H0：γ0=0，γ1=0，考察初步核算数据的优良性。该假设是数据表示初步核算数据是无偏的。Holden和Peel（1990）[8]指出Mankiw-Shapiro方法的问题②一个无偏的预测可能与误差项存在相关性，这使得Mankiw-Shapiro方法失效。，并给出了检验初步核算数据是否具备无偏性的经典方法：

其中GDPCt为真实GDP的最优组合预测，GDPPt为GDP初步核算数据，α为常数项，et为误差项。考虑原假设H0:α=0，拒绝该原假设是初步核算数据存在偏差的证据。

初步核算数据的有效性意味着，在t时刻可用的信息不能预测初步核算数据的预测误差GDPCt-GDPPt。根据Sinclair和Stekler（2013）[2]的思路，满足有效性的初步数据应符合：预测误差不能依赖于预测误差的滞后项，即考虑如下模型：

考虑原假设 H0:βk=0(k=1，2，...，K)，如果不能拒绝该原假设，则GDP初步核算数据满足有效性。Sinclair和Stekler（2013）[2]建议考虑一阶滞后模型，本文考虑了多个滞后模型，并使用AIC准则选择滞后阶数，从而考察数据的有效性特征。

1.3 测度初步核算数据与最优预测之间的“距离”

为了考察初步核算数据是否能很好地反映真实的经济运行情况，还需要比较初步核算数据与最优预测之间的距离。本文采用Sinclair和Stekler（2013）的距离函数，对两个向量x1和x2，定义如下的距离函数：

1.4 对比初步核算数据、最优组合预测与美国GDP的匹配性

对于数据使用者来说，只有初步核算数据能满足其及时性的需求。因此，对比初步核算数据、最优组合预测与其他经济变量的匹配性，可以判断当使用初步核算数据进行相关经济分析时，是否能得到真实的经济运行情况，如经济拐点信息等。本文考虑在时域-频域上考虑数据的匹配性。Rua（2010）[9]基于小波分析建立了一个相关性的测度指标，该方法便于同时考虑时域与频域特征，提供更多信息使得我们更好地理解经济变量之间的匹配性。考虑一个时间序列x(t)的连续小波变换定义为：

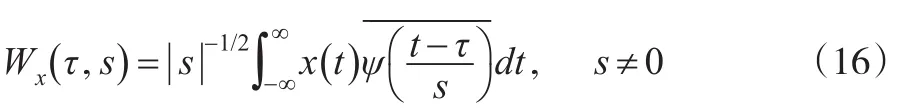
式（19）使得可以从小波变换还原时间序列x(t)。另外，母函数ψ(t)还必须满足：

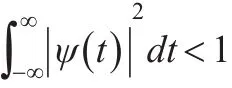
从式（20）可以发现小波函数必然具有振荡性。x(t)的小波变换具有一些有用的特征。如：可以用小波的能量谱来衡量某一时点某一频率下的数据对整个时间序列方差的贡献。对时域和频率进行积分就可以得到时间序列的方差：

另一方面，可以使用交叉的小波谱来衡量两个时间序列在时域-频域空间上的相关性。给定两个时间序列x(t)和y(t)，那么可以定义交叉的小波谱为：

一般而言，如果选取的母函数为复数型的（如Morlet母函数），则交叉小波谱也为复数。基于式（21）和式（22），Rua（2010）[9]建议使用如下形式的相关系数来捕捉时域-频域空间上两个时间序列的相关性：

其中，R[·]表示取复数的实部。其取值在-1到1之间[9]。式（23）建立的相关性测度使得可以同时考虑时域和频域，因此可以在研究经济变量的匹配程度时，同时考察时间维度和频率（或周期）维度上的情况，提供更多信息以便更好地理解经济变量之间的匹配程度及其时变特征。

2 我国季度GDP初步核算数据的质量评估

2.1 数据来源

本文选取2000年第一季度至2016年第四季度的GDP数据进行分析。数据来源于2000年1月至2018年4月的《中国经济景气月报》，数据单位：亿元。为了计算方便，将所有GDP数据除以10000，即将GDP数据单位换算为万亿元。美国季度GDP数据来源于世界银行数据库。

2.2 最优预测组合的估计

最优预测组合的估计需要计算初步核算数据、初步核实数据和最终核实数据之间的协方差及其各自的方差，因此需要先讨论GDP时间序列的平稳性特征。初步核算数据、初步核实数据和最终核实数据都包含明显的趋势。那么，该趋势究竟是确定性的时间趋势还是随机趋势？为此，采用单位根检验考察数据的平稳性。使用Dicker-Fuller单位根检验发现我国GDP数据（包括初步核算数据、初步核实数据和最终核实数据）是含时间趋势的平稳序列（均在1%的显著性水平下拒绝了存在单位根的原假设）；使用Phillips-Perron单位根检验，同样在1%的显著性水平拒绝了存在单位根的原假设；考虑到结构突变影响单位根检验功效的可能，使用Enders和Lee（2012）[10]的单位根检验同样证实了GDP数据是平稳序列的结论。因而，初步核算数据、初步核实数据和最终核实数据的方差、协方差是可以计算的。

基于2000年第一季度至2016年第四季度的GDP数据，本文依据式（6）至式（10）计算最优组合预测。经计算=0.135479，=0.308789 。因此，真实GDP的最优组合预测为

2.3 数据质量评估

首先，使用Holden和Peel（1990）[8]给出的检验初步核算数据是否具备无偏性的方法，考察初步核算数据是否为GDP最优组合预测的无偏估计。为了检验的可靠性，本文除了通常的基于最小二乘的标准误计算方法外，还考虑了基于Newey和West（1994）[11]的标准误计算方法。在Newey-West方法中，采用bartlett核，滞后阶数 q=[4(T/100)]29。表1给出了Holden-Peel检验的结果。在5%的显著性水平下，拒绝了原假设，且常数项的估计为0.071＞0，即初步核算数据低估了真实GDP数据。这可能是由于在初步GDP数据的核算中采用“核计+推算”的方式，其推算部分使用了较为保守的做法。

表1基于Holden和Peel（1990）[8]的无偏性检验

另一方面，本文也考虑基于Mankiw和Shapiro（1986）[11]方法的数据质量检验方法。表2给出了该结果。表2中的结果也拒绝了原假设，因而初步核算数据存在低估偏差。

表2 基于Mankiw和Shapiro（1986）[11]方法的检验结果

除了在初步GDP数据的核算中采用“核计+推算”的方式，其推算部分使用了较为保守的做法可能造成的偏误之外，初步核算数据的有效性意味着：初步核算数据的预测误差GDPCt-GDPPt不依赖于其滞后项。式（14）给出了相关的模型。表3给出了该检验结果。检验结果不能拒绝原假设；同时，如果基于式（14）检验假设包含常数项的原假设 H0:α=0，βk=0(k=1，2，...，K)，则在 10%的显著性水平下会拒绝该假设。因此，结合表1和表2的结果，本文推测初步核算数据存在低估真实GDP的情况，该偏误不依赖于预测误差的滞后项，因而初步核算数据满足有效性。

表3 基于式（14）的检验

接下来考察初步核算数据是否能很好地反映真实的经济运行情况，即比较初步核算数据与最优预测之间的距离。基于式（15）计算，使用2000年第一季度至2016年第四季度的GDP数据，估计得到F=0.01。因此，初步核算数据能与真实GDP数据很好地匹配。

为了考察使用初步核算数据是否能得到真实的经济运行情况，本文对比初步核算数据与美国季度GDP数据、最优组合预测与美国季度GDP数据之间的匹配性。在研究经济变量的匹配程度时同时考察时间维度和频率（或周期）维度上的情况，提供更多信息以便更好地理解经济变量之间的匹配性。图1给出了初步核算数据与美国季度GDP数据之间的匹配程度特征。图2给出了最优组合预测与美国季度GDP数据之间的匹配程度特征。

图1和图2中横轴、纵轴分别是时域、频域（或周期）的维度。因此，可以得到：某一时间点不同周期上变量之间的相关性；某一周期上，变量之间的相关性随时间的变化，即时变特征。对比图1和图2，初步核算数据与美国季度GDP数据时域-频域上的特征、最优组合预测与美国季度GDP数据时域-频域上的特征，发现两者非常接近，尤其在1年期之下的周期上各个时间点上两图中的相关性测度非常接近。因此，使用初步核算数据分析中国经济与美国经济的周期性特征，可以反映中国的真实经济运行与美国经济的周期性特征。即，中国季度GDP初步核算数据可以用于分析中国经济的运行现状。

图1初步核算数据与美国季度GDP数据的匹配程度

图2最优组合预测与美国季度GDP数据之间的匹配程度

3 结论

本文基于组合预测理论、无偏性和有效性检验及时域-频域上的匹配特征，提出了一个中国季度GDP初步核算数据质量评估的框架。将初步核算数据、初步核实数据和最终核实数据都视为是对真实GDP数据的预测，真实GDP数据是不可观测的，因而真实的预测误差也是不可观测的。本文推导了最优组合预测的权重，在此基础上，考察初步核算数据与最优组合预测之间的关系，即无偏性和有效性；在时域-频域上对比初步核算数据、最优组合预测与其他经济变量的匹配性，从而考察初步核算数据的质量。基于2000—2016年我国季度GDP的数据，研究发现：初步核算数据存在低估真实GDP数据的情况，这可能是由于在初步GDP数据的核算中采用“核计+推算”的方式，其推算部分使用了较为保守的做法。但研究支持初步核算数据的有效性，即初步核算数据的预测误差不依赖于核算时的可得信息；进一步地研究表明初步核算数据能真实地反映经济的运行情况。