基于加窗插值FFT和原子分解的间谐波检测算法

蒋建东， 杨鲲鹏， 耿莉莉

(1.郑州大学 电气工程学院 河南 郑州 450001； 2.国网河南省电力公司嵩县供电公司 河南 洛阳 471400)

0 引言

随着电力电子器件和冲击性负荷在电力系统中的大量应用，电网中间谐波的含量大量增加，引起了电压闪变、继电器误动作等多种危害[1].因此快速、准确检测出间谐波对改善电能质量和电网运行具有重要意义.

目前国内外专家已提出的间谐波检测方法主要有快速傅里叶变换(FFT)法、小波分析法、现代谱估计法、神经网络法[2-6]等.其中FFT算法最为经典且应用广泛，但在非同步采样时，FFT算法存在频谱泄露和栅栏效应问题[7].为解决这一问题，Jain提出在时域加矩形窗及频域插值来提高FFT算法精度[8].此后为能更好抑制频谱泄露，Hanning窗、Blackman窗、Nuttall窗等相继出现，插值算法也由单谱线插值发展为多谱线插值，故FFT算法的检测精度有了很大提高[8-11].但是，FFT算法在固定采样时宽下频率分辨率固定，当谐波、间谐波之间的频率差小于频率分辨率时，FFT算法无法准确检测.近年来，Mallat和Zhang提出的原子分解算法[12]满足信号多分辨率分析要求，在电能质量分析中逐步得到应用[13-17].文献[15]应用原子分解算法检测间谐波，但该方法在搜索最佳匹配原子时需要进行多次内积运算，计算量较高.文献[16]用PSO算法对匹配追踪算法进行优化，计算速度得到提高，但计算精度降低.

本文提出一种基于加窗插值FFT和原子分解的间谐波检测算法.对待分析信号进行FFT分析，求得峰值谱线值，并利用谱线干涉判据判断峰值谱线是否存在谱线干涉.当不存在谱线干涉时，则使用加窗插值算法校正峰值谱线，求得谐波、间谐波参数；否则使用原子分解算法在谱峰频率邻域内搜索最佳匹配原子，获取谐波、间谐波参数.此算法能分析出频率临近信号且计算量小于原子分解算法.

1 加Hanning窗插值FFT算法在间谐波检测中的应用

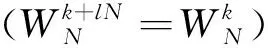
设待分析的信号为v(t)=Acos(2πft+θ)，式中：A为信号幅值；f为频率；θ为相位.对分析信号进行采样，采样频率为fs，采样点数为N，得到的离散信号为v(n)=Acos(2πnf/fs+θ).

为减少频谱泄露，对信号v(n)进行加窗，可得vd(n)=v(n)w(n)，其中w(n)为窗函数的时域形式.窗函数选取标准为主瓣窄、旁瓣小且衰减速度快.但这两个标准互相矛盾，实际中通常适当增加主瓣宽度达到抑制旁瓣目的.Hanning窗具有如下特点：1) 和其他余弦窗相比，有较小的主瓣；2) 第一旁瓣较低，且旁瓣衰减速度快；3) 基于Hanning 窗的双谱线插值，公式简单，计算量较小且易于实现.本文选取Hanning 窗截取信号，其时域表达式为w(n)=0.5-0.5cos(2πn/(N-1)).

对vd(n)进行DFT变换并忽略负频点，得到

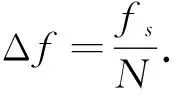
设真实峰值谱线k0左右两端的最大谱线和次大谱线为k1、k2，且k1≤k0≤k2=k1+1.它们的幅值为y1=|V(k1)|和y2=|V(k2)|.然后引入一个辅助参量，

α=k0-k1-0.5，α∈[-0.5,0.5]，

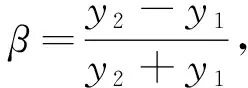
当采样点数N比较大时，利用多项式逼近，求得α=1.5β.所求信号频率修正公式为f=(k1+α+0.5)Δf；相位修正公式为θ=arg[V(ki)]-π·(α-(-1)i·0.5)，i=1,2；幅值修正公式为A=(y1+y2)(2.356+1.155α2+0.326α4+0.079α6)/N.

加窗插值提高了FFT算法的检测精度，但在固定的采样时宽下，频率分辨率固定.由于频谱泄露，信号间存在谱线干涉现象，当两信号频率相差较远，仅发生旁瓣干涉时，时域加窗是减小旁瓣干涉的一种有效方法；当谐波、间谐波频率接近，发生较严重的旁瓣干涉或主瓣干涉时，加窗插值FFT算法检测精度大幅下降，尤其当两信号的频率偏差小于频率分辨率时，该算法失去效用[3].

2 原子分解算法在间谐波检测中的应用

2.1 匹配追踪算法

原子分解算法根据信号自身特征，从过完备的基函数集合中，自适应选择一组最佳基函数对被测信号进行线性表示.这些基函数称为原子，由冗余原子构成的集合称为原子库.

在原子库中寻找最佳匹配原子的常用方法是匹配追踪算法(MP).该算法是一种贪婪自适应分解方法，根据索引方式对库中所有原子进行扫描，找出与待分析信号或残余信号最为匹配的原子(即该原子与信号内积值最大)，根据原子参数分析出相应信号成分并除去，然后形成残余信号.以此步骤对信号进行多次迭代，当满足迭代的终止条件时结束迭代，相应的匹配追踪过程也结束.

设H是维度有限的Hilbert空间，信号v∈H，D是H空间内的过完备原子库，首先从在原子库D中选择出一个原子gr(0)，gr(0)与信号v最佳匹配，故满足

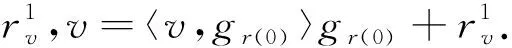
2.2 原子库的构建

过完备原子库中原子本身有着固有特性，可能只对某些与原子特性相近的信号有着较好的分解效果.为使原子分解方法能更好适应信号分解并减少计算量，针对某种信号特征生成的原子库称为相关原子库.电网中的谐波和间谐波信号均为正弦波，且认为在分析的时间窗内，信号是不变化的，故本文采用正弦量原子构造过完备原子库，其信号模型为gr(t)=krcos(ωt+φ)，式中：r=[ω,φ]为参数组；ω为待分析信号分量的角频率；φ为待分析信号分量的相位；kr是使‖gr(t)‖=1的系数.

上述原子库中原子参数具有连续性，使原子库规模达到无穷，MP算法找寻最佳原子需寻遍原子库，计算量巨大，不适用实际计算.因此需对原子库中原子参数进行离散化处理，离散后原子库依然保持过完备性.正弦原子库中原子参数离散为

利用原子分解算法分析信号时，每次迭代信号都需要与原子库中的每个原子进行内积计算，以寻找最佳匹配原子.对含有多个谐波、间谐波的信号，需进行多次迭代，计算量大，实用性受到限制.

3 基于加窗插值FFT和原子分解的间谐波检测算法

加窗插值FFT算法在分析谐波、间谐波时，有着计算速度快、分析精度高等优点，但是当信号中含有频率相近成分时，受谱线干涉与频率分辨率影响，加窗插值FFT算法检测精度下降甚至失效.原子分解算法在检测谐波、间谐波时不受谱线干涉影响且频率分辨率高，但是运算量大且分析精度不稳定.对此，本文提出基于加窗插值FFT和原子分解的间谐波检测算法.首先对信号频谱进行判定，在有谱线干涉情况下，使用原子分解算法，否则使用加窗插值算法.该算法避免了FFT算法的频率分辨率低和原子分解算法计算量大的问题.

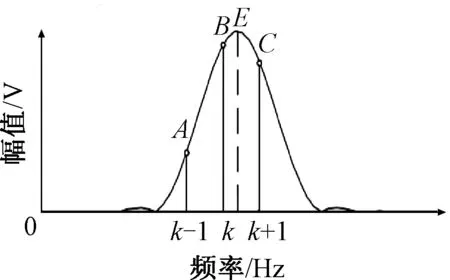
图1 单频率信号的理论频谱Fig.1 Theoretic spectrum of single-frequency signal

3.1 谱线干涉判定方法

峰值谱线是否存在谱线干涉可以用幅值判断法[18]来判断.假设窗函数的窗谱主瓣内至少有三条谱线，用任意相邻的两条谱线都能求得校正频率，因此取与峰顶比较靠近的三条谱线，如图1中k-1、k、k+1所示，A、B、C为对应谱线的幅值.用A与B、B与C分别使用比值校正法做频率校正，如果校正结果一样，则不存在干涉.

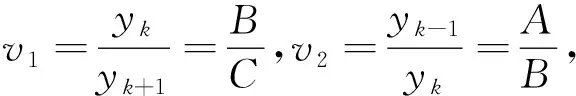
3.2 基于参数离散优化的MP方法

正弦量原子库中含有N个频率不同的原子，这些离散的原子频率中可能不含实际谐波、间谐波频率，提取到的最佳原子频率会和实际频率不匹配，产生较大误差.为了更好提取信号参数，对角频率离散参数优化为ω*=2πk/fs，则原子频率为f=fsω*/2π=k，从式中看出原子频率变化率为1 Hz.对于分析谐波、间谐波，1 Hz的频率分辨率就能很好匹配谐波、间谐波频率.

待分析信号进行FFT后，可求得最大谱峰对应频率fl，为原子分解算法的频率参数确定了大致的搜索范围.由于Hanning窗的第三旁瓣峰值约为主瓣峰值的0.3%，当相邻的谱峰间隔大于等于5个谱线间隔时，彼此之间影响较小，所以频率搜索范围定为k∈[fl-5Δf,fl+5Δf]∈Z.

由三角函数性质cos(α+π)=-cosα，可对原子离散相位优化：φ*=2πq/N，q∈[0,N/2-1]∈Z.然后根据最大内积符号，对相位φ进行修正，即

对离散的原子角频率和原子相位进行优化后，原子库中原子数量从N2降低到10Δf·N/2，且只有在谐波、间谐波存在谱线干涉时才用原子分解算法进行检测，运算量显著减少.

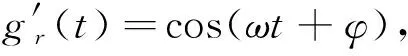
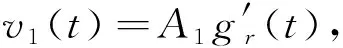
3.3 算法步骤

首先用Hanning窗截取信号并对信号进行FFT分析，搜索峰值谱线值和它两端的谱线值，使用幅值判断法判断是否有谱线干涉，根据判定结果选择合适算法，算法步骤如下.

(1) 首先用Hanning窗截取信号并对截取的信号进行FFT分析，求得信号频谱.

(2) 搜索最大峰值谱线kl，峰值为V(kl).然后找到与最大峰值谱线相邻的谱线kl-1和kl+1，计算出它们的幅值V(kl-1)、V(kl+1).

(3) 利用幅值判断法判断峰值谱线是否存在谱线干涉.

(4) 根据判断的结果，使用不同算法进行分析.若没有谱线干涉，则直接使用加窗插值算法检测参数；若有谱线干涉，则选用原子分解算法对参数进行估计.

(5) 计算残余信号.重复步骤(1)～(5)，分析出信号中所有的谐波和间谐波后，迭代终止.

4 算例分析

为证明本文算法准确性，假设含有多个谐波和间谐波信号模型为

式中：基波频率为50 Hz；幅值为380 V；初相位为30°.其余谐波、间谐波参数如表1所示.Matlab仿真时，设定采样频率为3 kHz，采样点数为1 024.

(1) 采用加窗插值FFT算法对信号进行分析，仿真结果如表1所示.

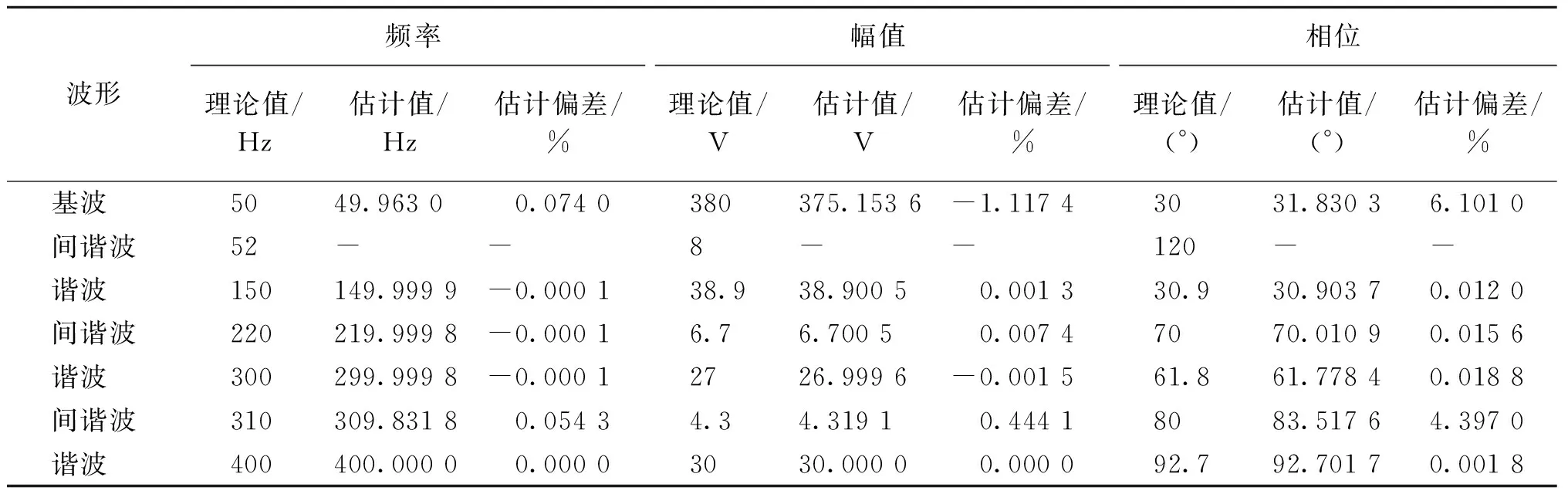
表1 参数估计结果

从表1可以看出只用加窗插值FFT算法检测谐波、间谐波时，若不存在频率相近成分时，检测到的谐波、间谐波的幅值、相角和频率参数精度非常高，基本接近理论值；而当间谐波的频率接近谐波时，间谐波不仅检测不出来，还影响了谐波的检测精度.

(2) 采用本文算法对信号进行分析，仿真结果如表2所示.

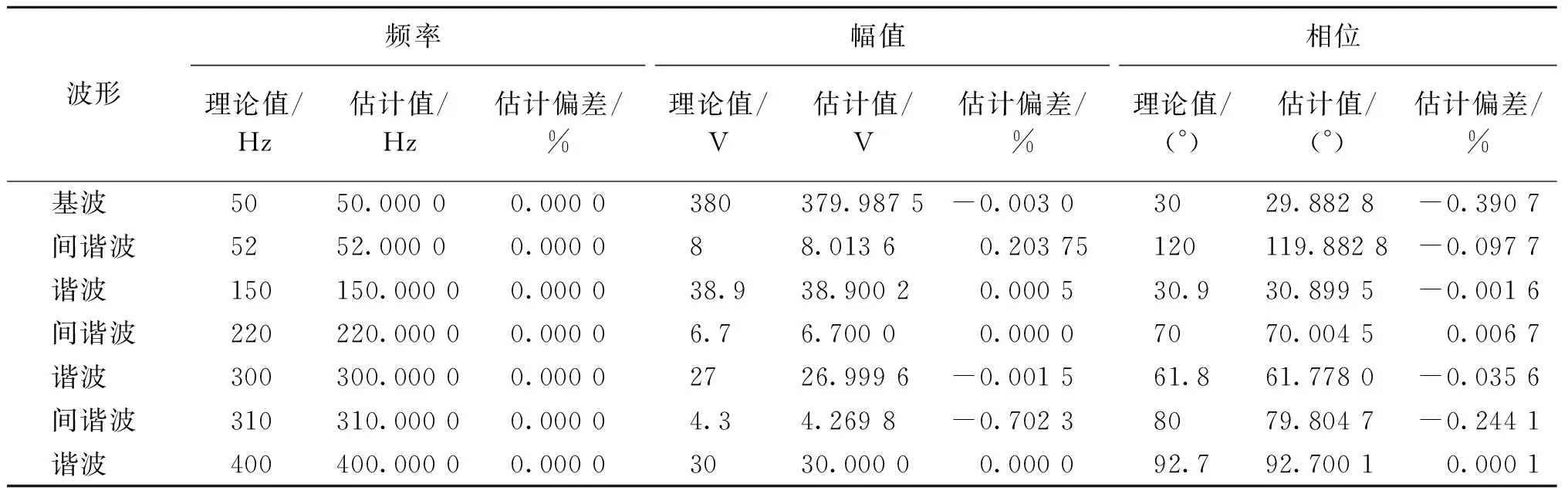
表2 参数估计结果

本文算法对信号参数的分析结果如表2所示.从表2可以看出，本文提出的混合算法能有效检测出频率相近的谐波、间谐波，弥补了加窗插值的不足，而且对频率、幅值、相位的检测精度很高，尤其对频率来说，几乎没有误差.

(3) 采用本文算法对含有噪声的信号进行分析，信噪比为70 dB，仿真结果如表3所示.分析表3结果可知，本文算法具有较好的抗噪性.

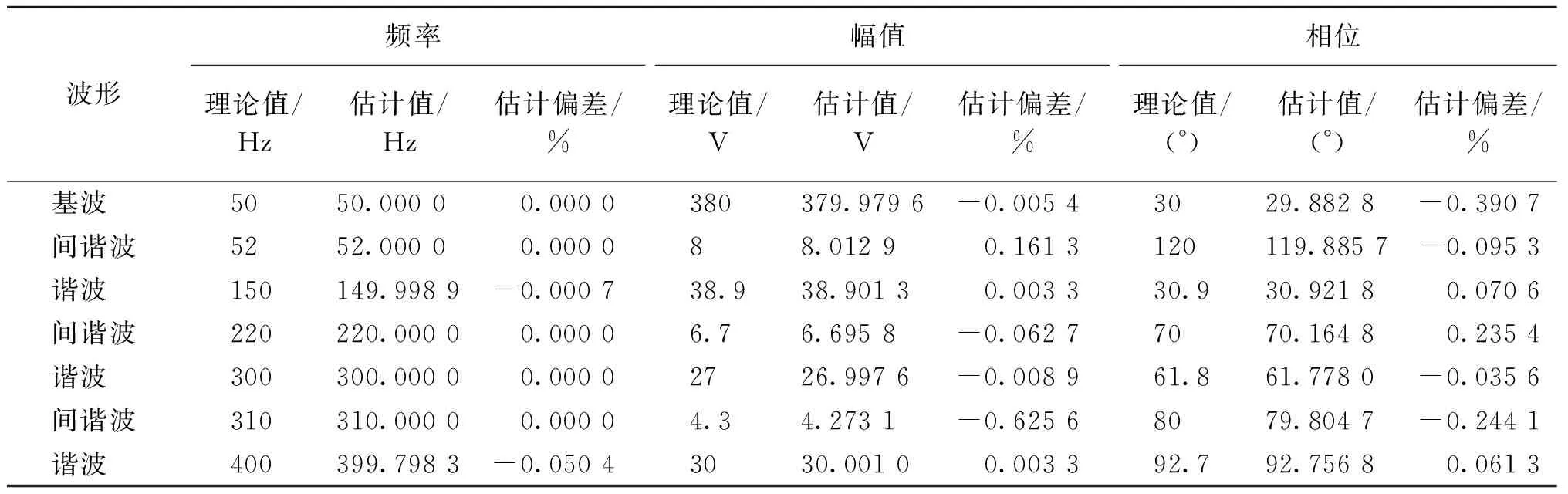
表3 参数估计结果

5 结论

加窗插值和原子分解算法都是间谐波检测的有效算法.加窗插值算法具有速度快、精度高的优点，但频率分辨率有限，无法分解出频率相近的谐波、间谐波信号，而原子分解算法具有无限频率分辨率的优点，但计算量大、速度慢，本文结合两个算法的优点提出了混合检测算法.该算法通过判断峰值谱线是否存在主瓣干涉来选择不同的算法，既能分解出频率相近成分，又减少了原子分解算法的计算量.算例分析表明，本文算法对谐波、间谐波进行检测可以取得较为满意的结果.