VOR系统方位角正交相关测量方法*

张 一，张 斌，贺 杰

（空军工程大学信息与导航学院，西安 710077）

0 引言

甚高频全向信标（very high frequency omnidirectionalrange，VOR）系统，又称为伏尔系统，广泛应用于国内外机场。它是一种近程的无线电导航系统，由地面发射台和机载设备组成，同现代飞机上的飞行管理系统和自动飞行控制系统配合工作，完成飞机的导航和进近着陆过程。随着数字技术的发展，机载无线电导航系统的功能越来越强，对性能指标的要求也越来越高，传统的信号处理算法已逐渐不能满足系统的性能要求［1］。同时，随着科技发展，飞机着陆引导信号受到周边电磁环境的影响越来越严重，据不完全统计，近60 %的事故发生在下降、进近和着陆阶段。同时，跑道附近的建筑物、停机坪、塔台等对导航信号产生多径反射，对跑道上空特定空间电磁场产生干扰，也会严重影响导航的精度，从而引发安全事故［2］。

传统的VOR测角方法，是基于基准相位信号和可变相位信号的过零检测［3-4］，在受到多路径等干扰的情况下，可变相位信号的零点有可能发生较大的偏移，导致较大的测角误差，从而导致导航事故的发生。因此，改进信号的处理算法，提高导航信号的抗干扰能力，在复杂的电磁环境中实现对导航精度的提高，可以既经济又便捷地提高安全系数，不需要更换现有的导航设备或者对着陆环境进行较大的改善。

1 VOR信号格式

伏尔测角系统工作在108 MHz～118 MHz甚高频波段，在360°范围内发射方位信号。伏尔信标发射的方位信号包括两个基本部分：基准相位信号和可变相位信号。VOR系统的原理是根据可变相位信号与基准相位信号的相位差来导航。基准相位信号的相位在发射台的各个方位上相同，可变相位信号的相位随发射台的径向方位而变化。飞机磁方位决定于基准相位信号与可变相位信号之间的相位差。可变相与基准相信号同步发射，磁北极两者相位相差0°，随着飞行器相对于地面台水平面方位的不同，两者的相位差从0°～360°变化。机载设备接收来自地面台的发射信号，并测量出这两个信号的相位差，就可得到飞机磁方位角，再加180°就是方位角。测量的基本原理是测量地面台发射的基准相位30 Hz信号和可变相位30 Hz信号的相位差，计算二者的相位差是VOR系统信号处理的关键所在。

伏尔信号是一个复合调制的复杂信号，信号表达式为

其中，Em为载频信号振幅，φm是可变相位角，随飞机测得的伏尔信标台磁方位角变化而变化，Ω1=2 πF1（F1=30 Hz），Ω2=2πF2（F2=9 960 Hz），其中是对载频信号进行幅度调制的第1项调制信号，调制频率为30 Hz，包含与伏尔信标台磁方位角φm，是相位式测角中的可变相位信号，是对载频信号进行幅度调制的第2项调制信号，调制频率为9 960 Hz，是相位式测角的基准相位信号［5］。

VOR信号经过包络检测器，（包络检测器选取10 KHz的带通滤波器）信号的载波部分就被滤去，剩下30 Hz可变相位信号和9 960 Hz调制信号：

将该信号分送两个滤波器用以得到可变相位信号和基准相位信号［6-7］。如图1所示。

图1 信号处理过程

1）将信号通过中心频率为30 Hz的低通滤波器，得到可变相位信号：

2）将信号通过中心频率为9 960 Hz的带通滤波器，取出受到副载频调制的调频信号：

再将该调频信号进行解调，对该调频信号进行解调时，先对其进行硬限幅，得到方波信号，再将方波信号送入微分器，此时微分器输出信号脉冲的频率变化正好反映了30 Hz的变化速率。再进行包络检波，可得到30 Hz的基准相位信号［8-10］。如图2所示。

图2 解调过程

2 测角原理

2.1 传统测角原理

传统的VOR测角方法，是基于基准相位信号和可变相位信号的过零检测，由相位比较器测得可变相位信号的移相，即可确定用户相对VOR台的方位。相位比较器的原理是：分别将基准相位30 Hz正弦波和可变相位30 Hz正弦波进行过零检测，以基准相位正弦波为基准，一旦检测到其正向过零点计时器开始计数，检测到可变相正弦波正向过零点计时器停止计数，计算出其相差点数，同时计时器清零。系统测角的分辨率为

创造性思维是思维能力的核心，是在穿透客观事物本质及其内部联系的基础上产生的卓越思维。由于采用不成熟的防御方式更容易表现躯体化、退缩、幻想、抱怨及被动攻击等，中间型防御方式则为理想化、假性胜利及反作用形成，而成熟的防御方式则包含幽默、升华及压抑，所以改变不成熟的防御方式有特殊的积极意义。在防御方式上予以积极支持，有利于创造性思维发挥。不同的创造性任务在体现创造性思维方面不同，消极情绪被激发时用于创造的认知资源转向产生一种防御物，个体的高创造性表现受限，负性思维直接影响焦虑水平[6]。情绪和创造性思维本身具有复杂性[7]。

式（6）中，fs为采样率，T 为30Hz正弦信号的周期［10］。

因为传统的测量方法是基于信号相位点的过零检测，当噪声较大时，信号的过零点极易受到影响，而此时，信号上的其他点对测量的结果毫无贡献，这就造成了3个问题，一是测量方法的抗干扰性差，二是测量数据未得到充分的利用，三是受到采样率的影响，当采样率高时能保证测角精度但计算量较大，当采样率低时又不能保证测角精度。

2.2 相关法测角原理

相关法是比较信号间相似程度的一种常用方法，在实际中应用较为广泛。数学上用相关函数来衡量相关性的大小［11］。本文将基准相位信号和基准相位延迟后的信号分别与可变相位信号做相关性运算，利用相关函数来求解方位角的大小。在相关运算的过程中，充分利用了测量的每一个数据，可以降低噪声干扰对测量结果的影响。

由式（5）基准相位信号，可知，将基准相位信号延迟0.5π后，得到延迟相位信号

将可变相位信号分别与基准相位信号和延迟0.5π相位后的延迟相位信号分别做相关性运算。用k1表示可变相位信号与基准相位信号的相关运算结果，用k2表示可变相位信号与基准相位信号延迟相位后的信号的相关运算结果，则

其中，T为一个周期。则

由计算结果可知，可变相位φm的正切值与相关运算的结果k1和k2的比值存在线性关系。

由相关性运算的结果知，当k1、k2均大于零时，可变相位信号中的方位角φm小于90°；当k1小于0时，方位角φm大于90°小于270°；当k1大于0，k2小于0时方位角φm大于270°小于360°。

当k1小于0时，

当k1大于0，k2小于0时，

当 k1、k2都大于 0时，

3 仿真与实测数据分析

利用Matlab对传统的过零检测和正交相关测角法进行仿真分析，分别加入不同大小信噪比的随机信号噪声，观察利用两种方法测量角度，测量结果在不同信噪比条件下所受到的影响。

1）首先分析传统过零检测方法中，测量误差受信噪比的影响。当信噪比为20 dB时，测量误差如图3所示。

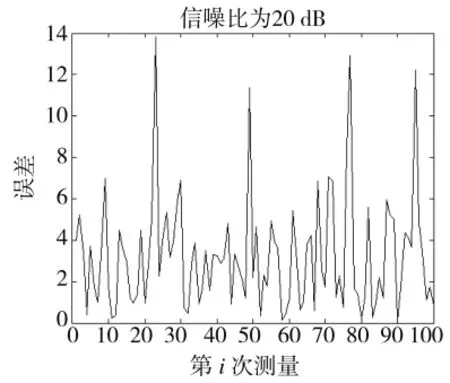
图3 信噪比为20 dB时传统方法测量误差

当信噪比为30 dB时，测量误差如图4所示。

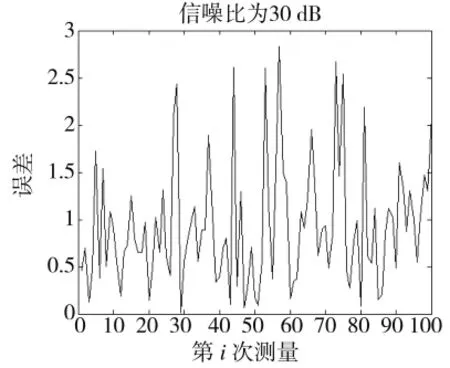
图4 信噪比为30 dB时传统方法测量误差

当信噪比为40 dB时，测量误差如图5所示。

图5 信噪比为40 dB时传统方法测量误差

由仿真分析可知，用传统方法测量方位角时，当信噪比为20 dB时，误差在15°范围内；当信噪比为30 dB时，误差在3°范围内；当信噪比为40 dB时，误差在1°范围内。只有在信噪比大于40 dB，测量误差小于1°时，测量结果才比较准确。同时说明了传统方法测量方位角，极易受到噪声的干扰。

2）对正交相关法测量方位角的方法进行仿真分析。当方位角确定时，不同信噪比的情况下，测量误差的大小。误差的大小用误差的绝对值来表示。

当方位角为60°时，误差测量误差的大小随信噪比变化如图6所示：

图6 方位角60°时误差随信噪比变化

由上面的仿真分析可知，信噪比为0 dB时，即接收机接收到的VOR信号和随机噪声信号一样大时，误差范围在0.8°，随着信噪比增大，当信噪比大于10 dB时，误差收敛到0.2°，随着信噪比增大，误差越来越小，测量结果可靠度越来越高。

接下来分析，信噪比不同时，使用正交相关测量方法的误差。当信噪比为0 dB，计算所得角度与实际方位角的误差，如图7所示：

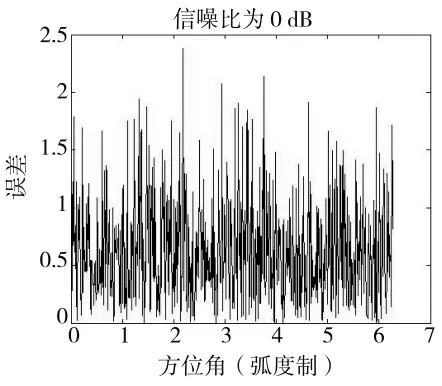
图7 信噪比0 dB时误差

当信噪比为10 dB，计算所得角度与实际方位角的误差，如图8所示。

当信噪比为20 dB，计算所得角度与实际方位角的误差，如图9所示。

将正交相关测角法应用到实际测量中，分析测量的实际误差。实验需要测量不同信噪比条件下，对不同角度的测量误差，设定预期方位角，用预期方位角和实际测量结果的差值来反映该方法的实测误差。

图8 信噪比10 dB时误差

图9 信噪比20 dB时误差

在实际测量中，由于噪声信号为不可控因素，无法通过改变噪声信号的大小来调整信噪比，只能通过改变信号功率的大小来实现不同信噪比条件下的实际测量。

当信号功率为-50 dBm，-30 dBm，-10 dBm时，对不同方位角分别测量10次，分析测量结果的误差，测量结果如下：

图10 不同信号下的测量误差

实测数据显示，当信号大小-50 dBm时，测量结果与设定的角度的偏差在±1.5°以内；当信号大小为-30 dBm时，测量结果与设定的角度的偏差在±0.4°以内；当信号大小为-10 dBm时，测量结果与设定的角度偏差在±0.1°以内。实测结果的误差与仿真分析结果在同一数量级，实测中的误差略微大于仿真分析的理论误差，是由于硬件设计中可能存在的其他噪声干扰。

4 误差分析

使用改进后的正交相关法测量方位角，减小了系统误差对实验结果的影响，最主要是减小了随机噪声对测量结果的影响，即使是在信噪比为0 dB（即噪声功率和VOR信号功率相当）时，误差大小也收敛在2°的范围内。因此，利用正交相关法来进行测量方位角，具有极好的抗干扰性，改进后的方法中，同样存在固有的系统误差，是由于对基准相位信号和可变相位信号进行采样离散化采样处理才可以进行相关性运算，在Matlab中进行仿真计算，离散化的采样，将会导致运算结果存在一定的误差。当信噪比较小（小于20 dB）时，系统误差不是主要的误差来源，噪声信号才是主要误差源。随着信噪比增大，随机噪声的影响逐渐减小，系统误差成为主要的误差源，误差在0.04°变化。

5 结论

在测角过程中，为了使测量结果更加精确可靠，应充分利用实测过程中的每一组数据。本文通过对传统的测角方法——过零检测法进行改进，用正交相关法计算飞机的方位角，通过理论说明，证实了此方法的可操作性，并通过仿真分析证明了该方法的精度确实优于传统的测角方法，在计算飞机方位角的过程中，提高了精度，具有十分优良的抗干扰性能。当前机场周边电磁环境较为复杂，该方法的提出可以有效地应对导航信号易受干扰的问题。该方法的应用，是基于现有的导航设备和导航信号格式，无须更换导航设备或者更改导航电文格式，也无需大幅度改善飞机着陆、进近时的机场周边环境，对于当前飞机的着陆进场，有着极为重要的应用价值。