基于全耦合时域模型的J型铺管管道内力敏感性分析

张榕恬，李 昕，刘锦昆

(1.大连理工大学 水利工程学院， 辽宁 大连 116024； 2.中石化石油工程设计有限公司， 山东 东营 257026)

近年来，随着世界能源需求的不断增加，人们对海洋的开发由近岸浅海逐渐扩展到了深海。随着世界能源需号铺管船已经成功完成2 775 m水深的铺管任务[1]，我国的“海洋石油201油号最大铺设作业水深达1 409 m[2]。对于波流荷载作用下的海底管道动力响应很多学者进行了试验模型研究[3-4]，常用的铺管方法有S型铺管和J型铺管，求解管道铺设过程中的受力方法包括自然悬链线法，刚悬链线法，奇异摄动法[5]，有限差分法，非线性有限元法[6]以及机器人手臂法[7]。

于友国等[8]利用ANSYS编程迭代的方法，有效的避开了接触问题，分析了管道悬跨长度和脱离角与水平力之间的关系。周巍伟等[9]对S型铺管进行了动态有限元分析计算，并对影响因素进行了分析。叶茂等[10]利用Sesam软件求出船体响应，并作为位移荷载输入采用ABAQUS建立的J型铺管模型，研究环境荷载对管道受力特性的影响。王晶[11]通过使用AQWA水动力学软件确定船体运动RAO，再带入OCRAFLEX软件中求解J型铺管相关参数。

尽管国内外许多学者已经做了相关的研究，但其中大部分属于半耦合分析，即不考虑船体运动对管道的影响效应，或直接将船体RAO作用于管道上部解耦分析。但随着水深的增加，细长杆单元与大体积浮体之间的耦合(管道与船体)效应显著，包括：浮体的偏移引起的恢复力对管道的影响，管道由于海流作用产生的恢复力对船体的影响，管道由于动力和海流的作用对船产生的阻尼，管道的惯性力对船的影响，船或托管架与管道发生接触摩擦引起的阻尼以及管道的海底摩擦对船的影响，因此推荐使用耦合的方法进行分析[12]。

本文利用Moses软件，将船体-托管架-管道作为一个整体，考虑船体动态定位的方法，对J型铺管进行全耦合动力分析。同时比较铺设角度、管道特性、水深、环境荷载等参数的变化对管道应力和弯矩的影响。

1 理论分析方法

1.1 耦合运动控制方程

考虑环境荷载以及船体动态定位的共同作用，船体与管道整体运动时域耦合方程如下：

qwi+qwa+qcu+qdp

(1)

由于海底管道是小体积细长结构，因此流体作用在管道的力采用Morison方程求解，具体公式如下：

(2)

Moses软件为有限元分析软件，应用最小势能原理得到离散化耦合运动控制方程。将管道离散化为大变形梁单元，采用Newmark方法将微分方程转化为代数方程，使用Newton迭代法进行求解。

1.2 动态定位的模拟

管道铺设时船体由于受到海流、波浪等环境荷载的作用会产生很大的位移，导致管道受到极大内力。因此在管道铺设作业时，必须对船体位移加以限制。在浅水中，一般采用锚链系泊的方法，但在深水铺设时，由于锚链张力过大，而难以采用系泊定位的方法，因此动态定位的方法应运而生[13]。

动态定位是通过提供平衡环境荷载所需的推进器推力来实现平衡的方法。Moses中通过测量监控船体位移和速度与基准值的差值，即PD控制算法来实现平衡控制。PD算法是一种线型算法，它将设定值与实际输出值的偏差作为输入[14-17]，然后将偏差的比例(P)和微分(D)通过线性组合构成控制量，PD控制算法如下：

(3)

式中：Kp为比例增益系数；KD为微分增益系数；ε为各增量值与基准值之差。

2 计算模型

2.1 铺管船基本参数

采用Balder起重铺管船，表1给出了Balder铺管船的主要参数。

表1 船体主要参数

船体坐标系如图1所示，以船体形心点为坐标原点，x轴沿船尾指向船艏，y轴沿船左指向船右方向，z轴垂直海面向上。

2.2 边界条件

Moses软件采用Sensor单元和Prop单元模拟船体的动态定位。其中Sensor单元是传感器单元，用来测量实测位移及速度与基准值的偏差，经过计算得到船体所需推力，再通过Prop单元在船体的四个角点设置的推进器提供内力，最终使船体维持平衡状态。

图1坐标系定义

铺管系统的张紧器及铺管夹具的模拟采用Roller单元，它是一个特殊的广义弹簧单元，通过设置弹簧单元间隙和刚度对管道进行约束：管道顶端采用固定约束模拟张紧器，同时在J型塔中每隔4.5 m设置一个夹具固定管道，并保持一定倾角。

海底与管道的接触为刚性接触，考虑摩擦力，摩擦系数取0.55。铺管系统模型如图2所示。

图2铺管系统模型

2.3 基本工况计算参数

J型铺管系统基本参数如下：管道直径405 mm，厚度18 mm，管道总长1 200 m，密度7 850 kg/m3，弹性模量207 GPa，泊松比0.3。J型铺管塔架高90 m，铺设初始倾角80°，水深500 m。波浪荷载采用JONSWAP波谱，波高2 m，波周期8 s，船体重心处波浪荷载时程曲线如图3所示。

图3波浪波高时程

海洋表面流速为1 m/s，流速沿深度线性降低，海底海流流速为0 m/s。假设波浪和海流荷载方向一致。

2.4 影响因素工况选取

本文将分别从张紧器拉力大小、管道初始倾角、管道特性、水深以及环境荷载等五个方面分析对管道内力的影响。计算工况的具体参数取值如表2所示。

表2 计算工况的选取

3 结果与讨论

3.1 船体动态定位分析

在铺管过程中，采用动态定位的方法，防止船体在环境荷载作用下产生较大的运动。推进器只能控制船体水平运动，图4为基本工况下四个推进器共同作用下施加于船体的x向、y向总合力及z向总弯矩。由图4可知，推进器对船体的作用力较大，x向推力大于y向推力，其中x向推力最大值为686 kN，超过张紧器张力301 kN的2倍；y向推力最大值为324 kN，也大于张紧器的张力；z向弯矩最大值达到3.5×104kN·m。

3.2 特征参数变化对管道应力及弯矩的影响

为方便对比分析，本文选取管段各点全时域内最大应力和弯矩进行分析。图5～图10中，x轴为管道弧长，以海底锚固点为零点，指向船体张紧器方向；y轴为全时域内对应点的最大内力值。

3.2.1 初始倾角对管道内力的影响

初始倾角是J型铺管重要的影响因素之一，在其他参数相同的条件下，分别选取70°、75°、80°、85°和89°五个初始铺设角度，分析初始倾角对管道内力的影响，计算结果如图5所示。

由图5结果发现，管道的应力图和弯矩图上均出现两个峰值，一个在铺管船上管道释放点，一个在管道触地点附近。随着铺设角度的增加，触地点附近和脱离点的应力及弯矩均不断增加。这是因为铺设角度越大，管道悬跨部分减小，触底点前移造成曲率变小，因此应力及弯矩变大。另外触底点应力及弯矩始终大于脱离点，这是因为铺管过程中脱离点附近的内力是可控的，通过调节张紧器的张力，可防止脱离点处产生过大的内力。但当铺设角度接近90°时，由于轴向张力较小，管线脱离点处受环境荷载的影响较大，容易产生一定的应力集中。

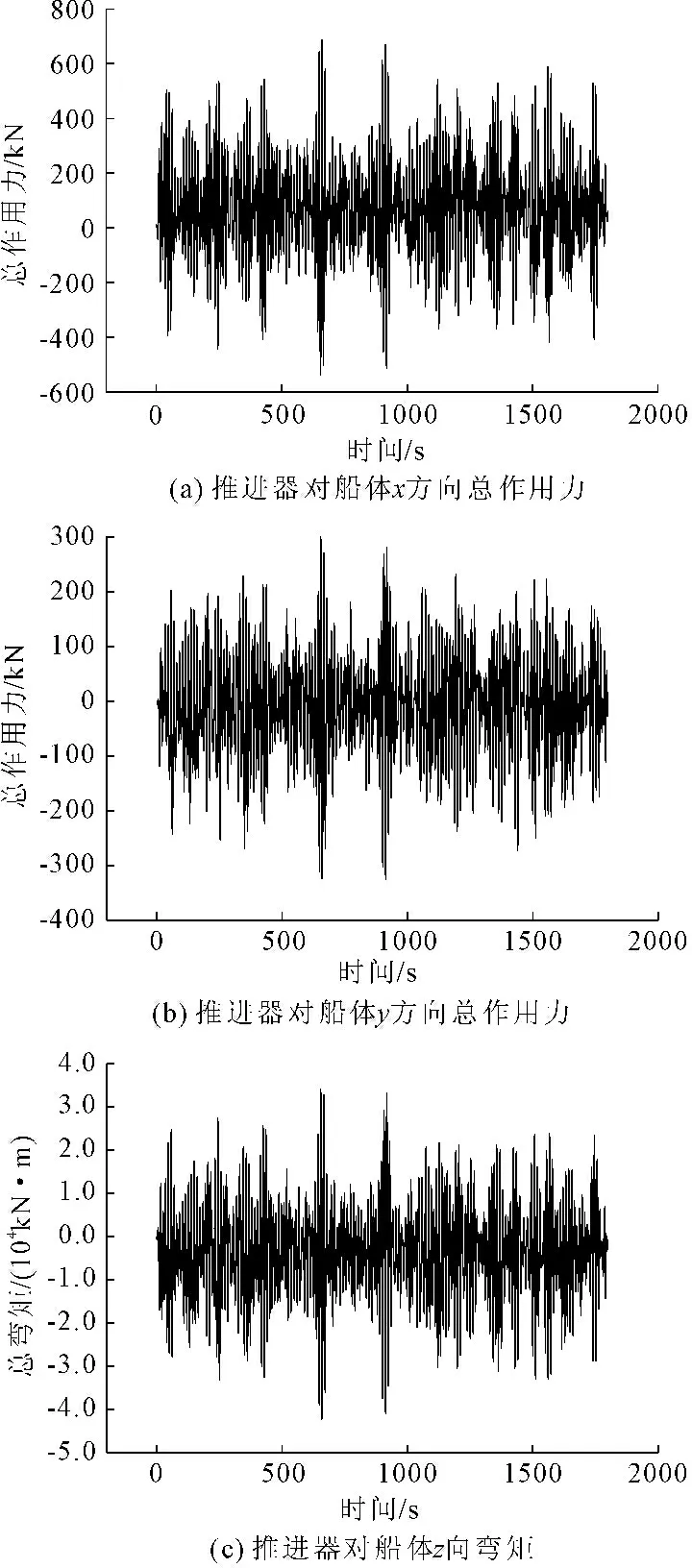
图4推进器对船体作用力

3.2.2 管道尺寸对管道内力的影响

为了分析管道尺寸对铺管的影响，分别选取表2管道尺寸中三组不同直径和厚度的管道，其应力和弯矩的计算结果见图6。

图6为不同管道特性下的应力及弯矩图，工况1和工况2厚度相同，工况2和工况3直径相同。由图6结果可以发现，管道尺寸对管道的影响主要体现在触底段附近，对释放点的内力影响不大。管道应力主要受管道湿重的影响，当直径相同时，随着厚度的增加，管道湿重增加；当厚度相同时，随着直径的增加，湿重减小。当湿重增加时，为保持一定的初始倾角，轴力需增加，因此轴向拉应力增加，因此等效应力增加。而弯矩主要受弯曲应力和抗弯截面系数两个因素的影响，本文的工况中，厚度相同，直径增加时，管道抗弯截面系数的增加程度大于弯曲应力的减小，因此弯矩增加。

图5 不同初始角度对最大弯矩和Von Mises应力的影响

图6不同管道尺寸对最大弯矩和Von Mises应力的影响

3.2.3 水深对管道内力的影响

为了研究海水深度对管道应力及弯矩的影响，在其他参数相同的条件下，分别选取水深为500 m、600 m和700 m，对管道的应力和弯矩进行了的分析对比，如图7所示。

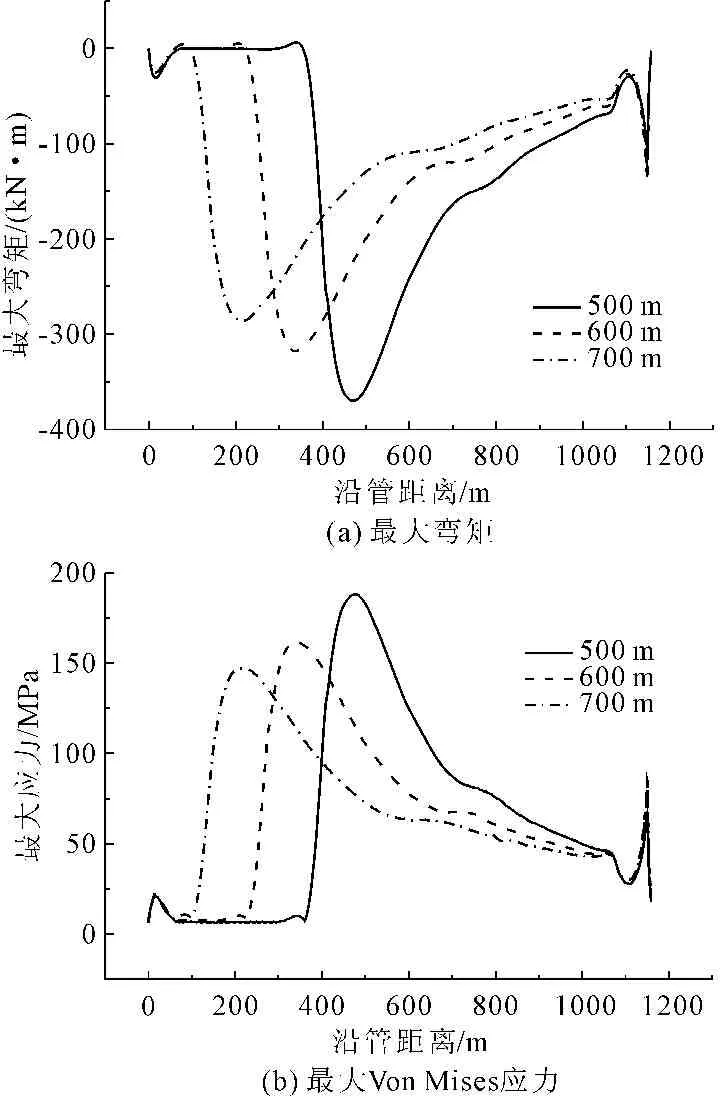
图7不同水深对最大弯矩和Von Mises应力的影响

由图7结果发现，在J型铺管过程中，水深对管道的影响主要体现在触底段附近，对释放点的内力影响不大。随着水深的增加，在相同铺设角度下，触底点后移，曲率减小，管道应力及弯矩不断减小。因此相同铺设初始倾角下，适当增加水深可改善管道内力，相应会增大张紧器的张力负担。

3.2.4 波高对管道内力的影响

对于波浪荷载的影响，本文从波高和作用方向两个方面进行考虑。首先为了研究波高对管道应力及弯矩的影响，在其他条件相同的条件下，分别选取波高1 m、2 m、3 m和4 m，对管道的应力和弯矩进行了分析对比，如图8所示。

通过计算结果可知，波高对管道应力及弯矩的影响主要在海平面附近，对触底点附近波高与最大应力及弯矩影响很小，几乎可以忽略，而在脱离角处应力和弯矩随波高的增大而增大。因此在J型铺管过程中，当波高在较小范围内时，可以忽略波高对管道的影响。

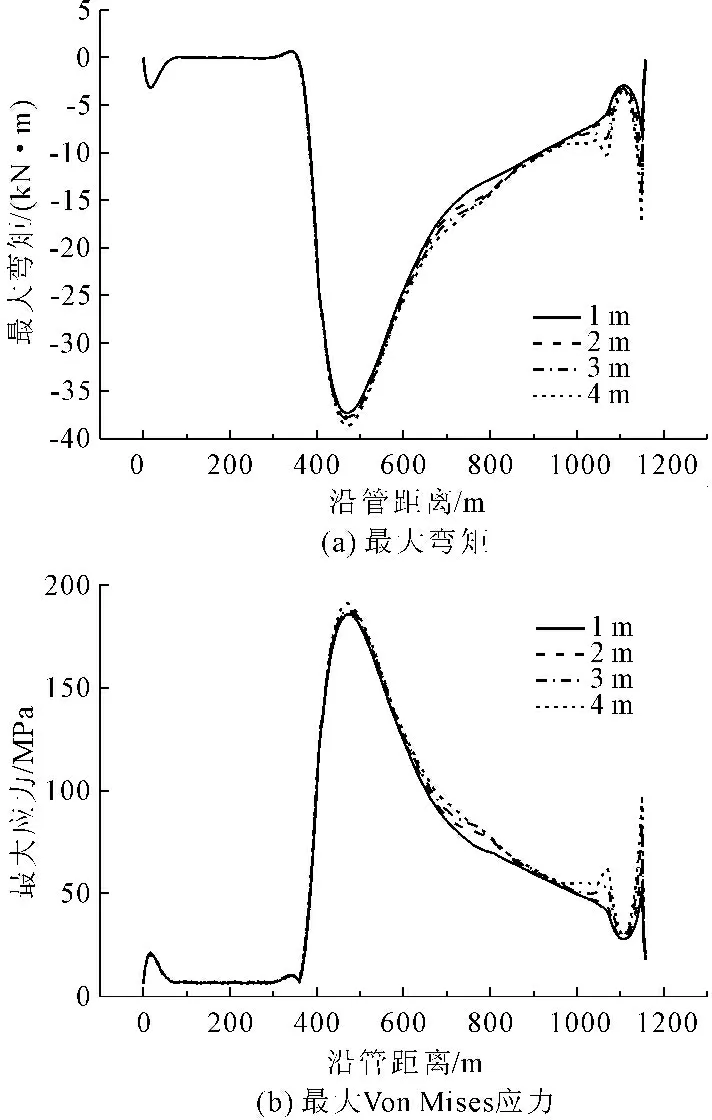
图8不同波高对最大弯矩和Von Mises应力的影响

3.2.5 海流流速对管道内力的影响

为了研究海流流速对管道应力及弯矩的影响，在其他条件相同的条件下，分别选取流速0.0 m/s、0.5 m/s、1.0 m/s、1.5 m/s，对管道的应力和弯矩进行了的分析对比，计算结果如图9所示。

通过计算结果可知，流速对管道应力及弯矩的影响较大，当海流流向为0°时，随着流速的增加，触底点处应力及弯矩均降低。这是因为当流速增大时，为了保持一定的倾角，张紧器张力增大，从而使曲率变小，弯矩减小；管道应力在触底点主要受弯矩影响较大，因此虽然轴力增加，但应力仍然降低。

3.2.6 荷载方向对管道内力的影响

为了分析荷载方向变化对管道的影响，假设波浪及海流方向一致，在其他条件相同的条件下，分别选取0°、45°、90°、135°、180°五个环境荷载输入方向下管道的应力及弯矩。

由试验结果可知，环境荷载的作用方向对管道的影响很大，当荷载方向为0°和45°时，即荷载方向顺着铺设方向时，应力及弯矩均较小；而当荷载方向为180°时，即逆流铺管时，应力弯矩值最大，此时铺管最危险。当荷载方向为90°，即横向铺管时，虽然应力及弯矩值相比逆流铺管时较小，但此时脱离点处应力超过了触底点应力，此时脱离点内力无法靠管道张力调节，因此也应避免横流向铺管。

图9不同流速对最大弯矩和Von Mises应力的影响

综合以上分析，我们发现管道初始倾角与环境荷载方向对管道触底点最大应力的影响最大。环境荷载中波浪对管道的影响非常小，几乎可以忽略，而海流流速的影响比波浪大很多。同时在铺设过程中水深的变化以及管道截面尺寸也对管道触底点应力有一定影响。

4 结 论

本文对于J型铺管进行全耦合动力分析，并对各个影响因素进行了讨论，讨论结果如下：

(1) 在J型铺管过程中，沿管道存在两个危险点，分别是管道触底点和脱离点。由于脱离点在船上，通过调节张紧器张力比较容易控制其内力，因此一般触底点应力弯矩均大于脱离点。

(2) 初始倾角和荷载方向是对J型铺管影响最显著的两个因素。倾角越大，管道内力越小，但由于张紧器拉力比较小，因此对于较剧烈的环境荷载，较难控制脱离点内力。管道铺设时应尽量顺流向铺管，避免逆向及横流向铺管。

(3) 管道的特性及水深对J型铺设管道应力的影响也较大。管道湿重越大，等效应力越大。而弯矩还要考虑管道抗弯截面系数的影响。

(4) 顺流向铺管时，流速越大，内力越小；逆流向铺管时，流速越大，内力越大。波浪荷载对J型铺管的受力影响非常小，只对海平面附近的管道有影响，基本可以忽略不计。