撞击荷载作用下板状岩体破坏特性数值模拟分析

廖志毅，唐春安，高军程，王海涛

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；2.大连交通大学 土木与安全工程学院， 辽宁 大连 116028)

近年来，随着人类对地下资源和空间需求的不断增加，岩体工程项目日益增多，所面临的工程问题随之增多。动态荷载作为一种常见的荷载形式，由爆破、钻探和撞击等施工扰动产生，广泛的出现在各类岩体工程中。研究表明，动态荷载作用下岩石的力学特性直接决定了地下结构的稳定性[1-4]。同时，岩体本身非均匀性导致地下工程问题变得更加复杂[5]。因此，充分研究非均匀岩体在动态荷载作用下的变形、损伤和破坏特性对有效指导岩体工程设计和施工具有重大的科学及工程价值。

在室内试验方面，落锤试验和霍普金森杆(SHPB)试验广泛的用于测试不同应变率条件下岩石的动态力学特性[6]。落锤试验是通过重物自由落体直接撞击在试样上产生动态扰动，而SHPB试验则是将岩石试样夹在入射杆和透射杆之间，通过子弹撞击在入射杆一侧，激发的应力波在入射杆中传播至岩石试样中。Whittles D等[7]采用落锤试验研究岩石荷载作用下的破坏特性，指出岩石破裂所需的能量和破碎程度随着应变率的增加而增加。Dai F等[8]研究了岩石试样长径比、摩擦和波形整形技术对SHPB试验结果的影响。Li X等[9]基于SHPB试验系统，分析了含预制单裂纹棱柱状大理石在动态冲击作用下的破坏特性。

以往的研究往往关注的是块体状岩体的动态力学特性，如圆柱体、立方体和巴西圆盘等，这类试样的长度和厚度相差不大。然而，对于具有较大长度与厚度比值的板状岩体研究相对较少。在这方面，Bertram A等[10]采用侧向撞击试验，将子弹撞击在岩板试样侧面中心处，研究了树脂和石灰岩II型裂纹扩展规律。汪亦显等[11]采用分离式SHPB装置，通过气压将小球以不同角度撞击岩板侧面中心处，指出岩板裂纹的长度和破坏面积随着撞击强度的增加而增加。单仁亮等[12]进行了石板中心冲击试验，研究花岗岩在低冲击速度下的裂纹扩展特性。

数值模拟方法，如有限元法[13-14]、离散元法[15]、边界元法[16]和DDA法[17]，被广泛的运用于研究岩石的力学特性。相比之下，数值模拟方法在观察岩体内部裂纹扩展趋势、获取岩体内部的应力场分布和对完全相同试样进行反复试验等方面具有显著优势。本文采用基于有限元应力应变分析的(Rock Failure Process Analysis，RFPA)数值方法，通过建立三维中心撞击数值模型，研究板状岩体在冲击荷载作用下的破坏特性。

1 数值方法

1.1 岩石非均匀性数值实现

非均匀性作为岩石本身一种重要的特性，直接决定岩体结构的稳定性和破坏模式。因此，这一特性必须在数值模型中得到充分考虑。RFPA方法基于有限元原理，假定岩体每一个单元的材料参数服从Weibull统计学分布。Weibull统计学分布如下：

(1)

式中：α为单元的某一力学参数；α0表示该参数对应的平均值。m为均质度系数，m越大时，岩石材料越均匀。

1.2 细观单元损伤演化

研究表明，岩体内部的损伤演化和材料的宏观破坏息息相关[18]。RFPA方法认为单元的应力状态满足最大拉应力准则或者莫尔库仑准则时，单元发生损伤。应力应变状态假定压缩为正，拉伸为负。具体介绍如下：

当单元的拉伸应力超过其单轴抗拉强度时，发生拉伸损伤。此时，单元损伤变量满足以下规律：

(2)

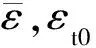
当单元的应力状态满足式(3)时，发生剪切损伤

(3)

式中：fc表示单元剪应力；φ为单元内摩擦角。对应的损伤变量满足如下规律：

(4)

式中：εc0和εcu代表发生剪切损伤时的应变和极限压缩应变；λc为单元压缩残余强度系数。

1.3 接触方法

精确的动态接触算法是实现撞击过程数值模拟的关键。刘晶波等[19]提出考虑动、静摩擦的可接触型的二维裂纹动态影响的算法。该方法能够有效地模拟裂纹上下表面在动态荷载作用下的接触过程。许多学者把该算法应用于模拟块体之间的碰撞过程并验证了其准确性[20-21]。本文通过把该二维接触算法扩展至三维情况，现实模拟三维块体的动态接触过程。

首先，建立数值验证模型，如图1所示，检验三维接触算法的准确性。模型由左侧撞击和右侧被撞击的三维弹性圆杆组成。撞击杆以恒定速度碰撞至被撞击杆左侧。监测点a位于被撞击杆中心的圆心处。被撞击杆的长度和直径分别为1.5 m和0.03 m，以保证应力波在杆中处于一维波传播状态。杆的材料参数为：弹性模量E=200 GPa，泊松比μ=0.28，密度ρ=7 800 kg/m3。

图1三维接触算法验证模型

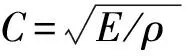
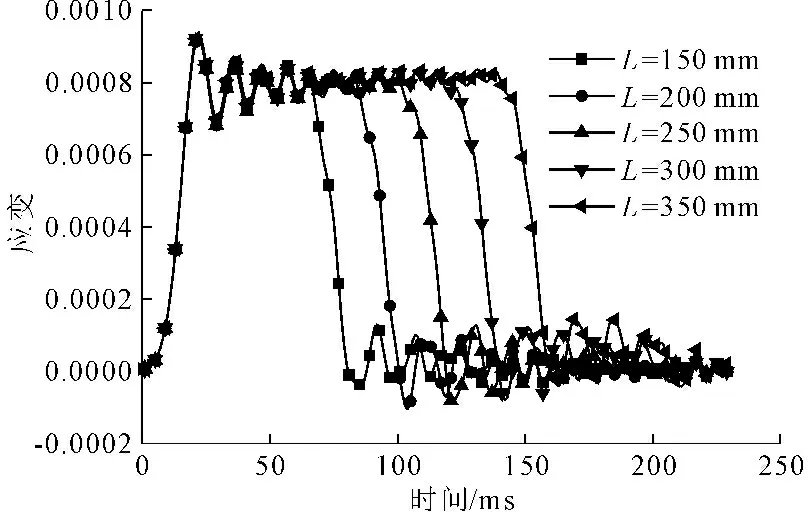
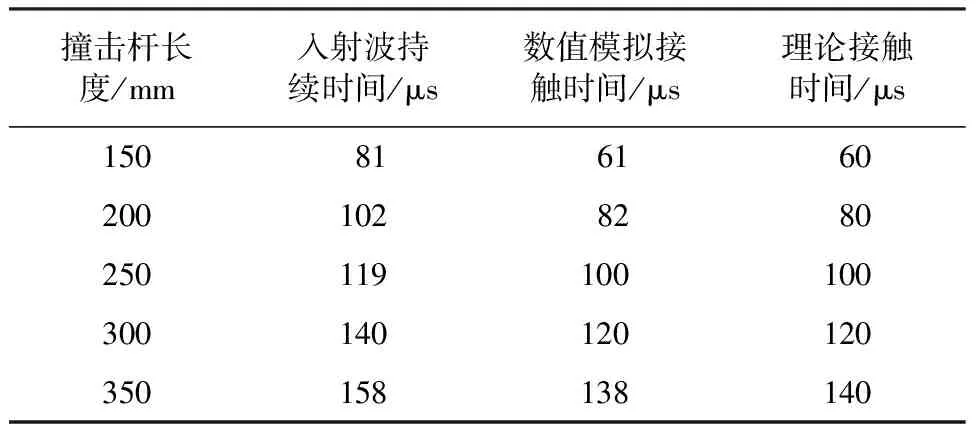
图2 不同撞击杆长度下入射波波形图

2 板状岩体撞击破坏数值模拟

2.1 数值模型

图3展示了三维视角下板状岩体中心碰撞数值模型图。Lr，Hr和Tr分别表示岩板试样的长度、高度和厚度。撞击子弹位于岩板前表面的中心。其高度，厚度和长度分别由Hs、Ts和Ls表示。撞击载荷是由子弹以匀速V垂直撞击在岩板上产生。岩板与子弹详细尺寸如下：Lr=200 mm，Hr=200 mm，Tr=20 mm，Hs=100 mm，Ts=20 mm和Ls=20 mm。材料参数如表2所示。

图3 模型示意图

2.2 数值模拟结果

图4对比了数值模拟与室内试验监测的入射波曲线。

图4入射波曲线图

其中，数值模拟结果选取的是撞击面中心处最大主应力与时间变化曲线，而试验结果则引用了单仁亮等[12]的试验监测结果。对比结果表明，数值模拟得到的入射波波形与试验入射波波形相似，这也说明了RFPA方法在模拟平板撞击这类问题的准确性。

以V=3 m/s情况下的数值试验为例来描述岩板的破坏过程。图5显示了撞击过程中四个不同时刻，岩板正面及背面的破坏模式。在撞击力的作用下，六条径向裂纹从撞击中心向外传播到岩板边界。然而，值得注意的是，这些裂纹的传播在岩板的正面及背面是不同步的。在撞击初期，即t=100 μs，破裂首先出现于岩板的背面中心处，而在正面中心处却没有发现宏观破坏。这是由于在撞击作用下，岩板正面处于压缩状态，而当产生的压缩波传播至岩板背面时，反射为拉伸波。由于岩石的抗拉强度远小于抗压强度。所以，岩板背面优先发生破坏。随着时间的推移，一方面，背面中心处的破坏迅速向外传播到岩板的边界(t=200 μs，如图5(f)所示)；另一方面，这些径向裂纹从岩板的背面逐渐渗透到正面(图5(b)，图5(c)和图5(d))。然而，裂纹沿厚度方向的扩展速度远低于沿径向的扩展速度。图6显示了室内试验岩板在中心撞击作用下的破坏模式。在他们的研究中，岩板在受到撞击后断裂成四块，与数值模拟结果非常相似。

图5 撞击速度3 m/s作用下岩板破坏过程图

图6室内试验破坏图

图7为不同撞击速度下岩板的最终破坏模式。观察模拟结果发现，随着撞击速度的增加，岩板的破坏模式趋于多样化和复杂化。对于撞击速度相对较低(V=3 m/s)的情况，岩板断裂由径向裂纹所致，而当撞击速度达到4 m/s，5 m/s和6 m/s时，岩板断裂由径向裂纹与环向裂纹共同所致。另外，相比径向裂纹的出现规律，这些环向裂纹首先出现在岩板的前表面。此外，随着撞击速度的增加，岩板中心处的破碎带面积也增加。

3 结 论

本文有限元分析方法的RFPA数值工具，采用Weibull统计学分布考虑岩石的非均匀特性，利用连续损伤力学方法分析岩石损伤演化过程，并通过引入三维动态接触算法处理块体之间接触过程，建立岩板中心撞击模型，分析了板状岩体的动态破坏特征，得到了以下结论：

(1) 采用的三维动态接触算法能够有效地模拟块体之间的撞击过程。在撞击作用下，数值和室内试验得到岩板内部激发的应力波波形具有良好的一致性。

(2) 在撞击力作用下，破裂首先出现在岩板背面中心处，并逐渐形成向四周边缘及正面延伸的径向裂纹。

(3) 在较低撞击速度作用下，岩板断裂由产生的径向裂纹所决定。随着撞击速度的增大，额外的环向裂纹逐渐出现，对岩板的断裂起到决定性作用。

图7不同撞击速度下岩板最终破坏图