深基坑开挖对邻近矩形地下通道变形影响研究

廖志坚，陈尚荣，曹传祥

(1.上海地矿工程勘察有限公司， 上海 200072； 2.上海理工大学 土木工程系， 上海 200093)

随着城市的不断发展，对地下空间的利用开发大大增加，出现了大量在密集建筑群中施工的基坑工程[1]。基于上海地区基坑工程出现“大、深、紧”的特点[2]，在城市基坑施工中，基坑工程常常紧邻于大规模建(构)筑物、综合管线、地铁隧道和交通干道等市政工程，并且施工现场场地狭小，因而不仅需满足基坑承载力和稳定性要求，还需对位移控制严格要求[3-4]。因此，在地下通道附近进行深基坑工程施工时，需对邻近地下通道产生的变形和力学规律进行分析研究，继而为复杂周边环境的类似基坑工程的设计研究提供参考，对邻近地下通道乃至地铁隧道的预加固措施技工借鉴和指导。

针对基坑开挖对邻近地下通道变形影响，国内外学者对该问题作出诸多研究工作。Peck R B[4]在第七届国际岩土力学与基础工程会议上针对基坑开挖实测数据及其发展现状首次发表了较为全面深入的报告研究。Lambe T W[5]通过对土体位移等基坑开挖影响因素以及基坑开挖实测数据对某地铁隧道的多个基坑工程的围护及支撑体系进行研究分析。Goh A T等[6]提出将两阶段法应用于基坑开挖对邻近既有隧道和桩基的影响。陈郁[7]基于弹性地基梁理论与Mindlin弹性半空间解得到隧道隆起定量计算方法和基坑开挖卸荷作用导致隧道结构的附加应力，通过与实测数据对比指出不同结果的原因。张治国等[8]基于两阶段法并考虑基坑开挖导致四周和坑底土体同时卸载的影响提出基坑开挖对邻近地铁隧道纵向变形的计算方法。

针对此问题，本文在前人的研究基础上[9-12]，基于上海市某深基坑邻近中环线地下通道的工程实例，根据两阶段法，求解基坑开挖对邻近地下通道变形的理论解答，采用弹性地基梁理论对地下通道的变形和受力机理进行讨论，推导出矩形地下通道的弹性地基梁计算方法。建立紧邻地下通道的深基坑开挖的弹塑性数值模型，模型同时考虑围护结构和矩形地下通道结构形式，建模过程中重点考虑地下通道刚度、埋深特点与普通建筑物的区别。

1 矩形地下通道变形预测曲线

基坑工程的设计不仅需要满足强度设计要求，还需满足变形控制要求[13]。本文基于上海市某深基坑邻近中环线地下通道的工程实例，根据基坑开挖对邻近矩形地下通道的变形影响研究，基于位移控制理论，采用两阶段法，对本文模型进行简化，如图1和图2所示。《基坑工程技术规范》[13](DG/TJ08-61—2010)中采用板式支护体系的弹性地基梁法不考虑土的结构作用，本文主要研究地下通道结构和围护结构变形机制，土体简化为均质土层。

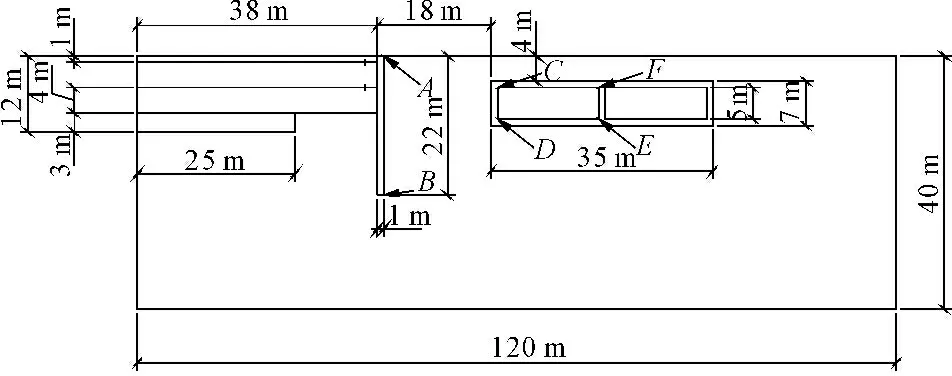
图1 基坑围护墙变形及坑外土体沉降示意图

图2基坑开挖二维平面模型示意图

1.1 基坑开挖对周围土体变形规律

1.1.1 基坑开挖效应的土体沉降曲线

假定围护结构墙后地表沉降曲线所围成的面积与围护结构侧向位移曲线所围成的面积相等，假定不存在地下通道的前提下，张陈蓉等[14]提出的坑外地表土体沉降预测公式：

(1)

式中：ωv,max为地面最大沉降值；H为基坑开挖深度；A为变形影响半径。

A=L/2×[0.069ln(H/L)+1.03]

(2)

基于位移控制理论，由拟合结果得到基坑开挖效应导致的任一点土体沉降曲线公式：

(3)

1.1.2 基坑开挖效应的土体水平向变形曲线

基坑围护结构的水平向变形预测曲线公式[15]：

(4)

式中：ωh,max为围护结构最大侧向位移。

基于位移控制理论，由拟合结果得到基坑开挖效应导致的任一点土体水平位移曲线公式[14]：

(5)

对于ωv,max和ωh,max值的确认，一般采用实测、经验值估算或者有限元软件进行模拟，其中实测值更为贴近工程实际，能够更好地研究基坑开挖效应导致的土体变形规律。《基坑工程技术规范》(DG/TJ08—61—2010)[13]中对于板式围护体系可以采用经验方法预估地表沉降和围护结构最大侧向位移，并且最大地面沉降值ωv,max=0.8ωh,max，围护结构最大侧向位移采用竖向弹性地基梁法计算。

1.2 矩形地下通道在土体变形条件下的变形规律及强度特性

基于本文1.1节的基坑开挖效应的土体沉降曲线和土体水平向位移曲线，可以得到任一点土体的竖向和水平向位移，利用位移控制法将土体的位移荷载施加于地下结构，从而进一步分析地下结构物的变形和内力。

研究基坑土体开挖卸荷使邻近既有地下通道结构产生相应的变形和附加内力，结合本项目依托的具体工程实例，主要计算靠近基坑侧通道侧壁及角点由于基坑开挖引起的附加应力和变形，同时分析通道底部由于基坑开挖引起的不均匀沉降以及附加应力。假设地下通道侧壁和地下通道底部均为Winkler弹性地基梁，土体和地下通道始终保持相互作用。

对于地下通道侧壁，可以简化为弹性地基梁，其水平位移微分方程可表示为：

(6)

其中：ω(z)为地下通道侧壁水平位移方程；xh为基坑开挖效应的水平向变形曲线；kh为水平基床系数，由现场原位试验确定或者参考类似工程经验值。当无条件进行现场原位试验时，可根据地基土的性质，按规范[13]选取。

对于xh的取值，选取本文1.1.1节基坑开挖效应的沉降曲线在基坑对称面上(y=0)上的值。

(7)

求解上述方程，即可得到地下通道侧壁由于基坑开挖产生的水平位移以及附加内力。

对于地下通道底部，同理也可以将其简化为弹性地基梁模型，其沉降曲线微分方程可表示为：

(8)

其中：ω(x)为底板垂直位移方程；yv为纵向沉降曲线方程；kv为垂直基床系数，由现场原位试验确定或者参考类似工程经验值。当无条件进行现场原位试验时，可根据地基土的性质，按规范[13]选取。

对于yv的取值，选取本文1.1.2节基坑开挖效应的水平向变形曲线在基坑对称面(y=0)上的值。

(9)

求解上述方程，即可得到地下通道底板由于基坑开挖产生的变形以及附加内力。

2 分析求解

本文依托于某深基坑开挖对邻近上海市中环线某地下通道影响研究，基于实际工程案例，利用Mathematica首先求得基坑开挖效应引起的围护墙(图2中AB段)侧向位移分布，围护墙的最大侧向位移值出现在基底附近，并处于基坑对称面上，且沿基坑对称面正态分布，如图3所示。

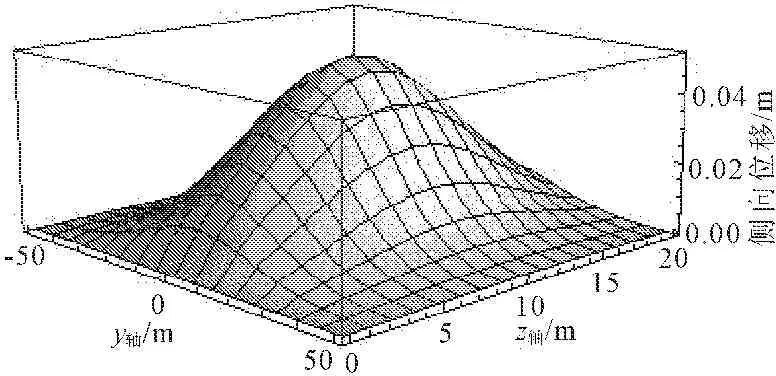
图3基坑开挖效应的围护墙侧向位移

基坑开挖效应引起的地表沉降分布，地表沉降的最大值出现在基坑开挖面附近，并处于基坑对称面上，且沿基坑对称面正态分布，满足基坑开挖引起地表沉降的一般规律，且基坑开挖效应引起的地表沉降区域半径约为4H，且该地表沉降规律与Hsieh P G等[16]的预测沉降曲线一致。如图4所示。

图4基坑开挖效应的地表沉降

2.1 靠近基坑侧矩形地下通道侧壁结构变形及附加应力分析

基于式(5)求得靠近基坑侧地下通道侧壁位置(图2中CD段)的土体位移，靠近基坑侧地下通道侧壁所在垂直面的最大土体位移值在基坑开挖深度H附近，并处于基坑开挖对称面轴线(y=0)上，且沿基坑开挖对称面正态分布，最大值约为4 mm，如图5所示。

基于位移控制分析理论，选取靠近基坑侧地下通道侧壁最大土体位移值所在的轴线，即y=0为分析对象，利用式(6)对靠近基坑侧地下通道侧壁附加内力和变形进行分析。其计算示意图如图6所示，边界及连续性条件为：

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

图5 靠近基坑侧地下通道侧壁位置的土体水平位移

图6计算示意图

利用Mathematica对式(6)在上述边界条件下求解，如图7所示。在基坑开挖深度范围内，靠近基坑侧地下通道侧壁水平向位移随着地下通道的埋深而增大，并在地下通道约底部位置附近达到水平向位移的最大值，最大值约为4.0 mm。由于围护结构侧向位移的最大值出现在基底附近，考虑到侧壁的埋深位置，认为基坑开挖效应引起的地下结构侧壁水平位移最大值与基坑开挖深度H有关。

图7靠近基坑侧地下通道侧壁水平变形图

对于地下通道侧壁附加应力分析，可由下式求出其剪力和弯矩。

(18)

(19)

2.2 矩形地下通道底部沉降及附加应力分析

基于式(3)求得地下通道底部位置(图2中DE段)土体沉降曲面规律，与地表沉降曲面类似，在地下通道底部位置所在平面上，最大沉降值出现在基坑开挖面附近约0.5H的位置上，并处于基坑开挖对称面上，且沿基坑对此面正态分布，且其最大沉降值约为0.015 m。靠近基坑开挖面土体有隆起现象，而地表土体为沉降现象。在上海地区围护结构为钻孔灌注桩的监测数据显示，桩体回弹现象明显，其原因可能基坑土体回弹，造成桩侧摩阻力下降，以及主动土压力与被动土压力的中性点位置有关，如图8所示。

图8矩形地下通道底部土体沉降图

通过与地下通道顶部位置(图2中CF段)土体沉降曲面图进行对比，见图9，可知土体沉降规律在土体深度方向一致，且在深度方向变化量较小。

图9矩形地下通道顶部土体沉降图

基于位移控制分析理论，选取地下通道底部位置土体最大沉降量所在直线(y=0)为分析对象，利用式(8)对地下通道底部沉降及附加内力进行求解分析。其计算示意图及边界条件在2.1中已述。

利用Mathematica对式(8)在上述边界条件下求解，地下通道底部变形量的最大值在1.2 mm左右，且整个地下通道的变形量基本一致，考虑到地下通道位置离基坑开挖面最近处为2H，考虑到地下通道底部土体沉降的影响范围及其沉降值，认为该地下通道变形量的值在一定程度上符合实际。

对比于地下通道顶部的变形，基坑开挖效应引起的地下通道顶部变形随着远离基坑开挖面而减小，其最大变形量约为3 mm左右，基本呈线性变化，与地下通道顶部在该位置的土体沉降值相一致。由其对比可知式(8)在一定深度范围的预测效果更好。

对于地下通道底部附加应力分析，同样可由式(18)、式(19)求出其剪力和弯矩。

3 有限元分析

基于理论研究的局限性和实际工程的复杂性，本文依据实际工程案例，选取其典型剖面进行二维数值模拟分析，其基坑开挖二维平面模型示意图如图2所示。取基坑半剖面为研究对象，该基坑分为四级开挖，其中最后一级开挖为下沉院区域，开挖深度3 m，长度25 m。第一级开挖深度1 m，长度38 m，第二级和第三级开挖深度均为4 m，长度38 m。其中在第一级开挖和第二级开挖之后分别设置一道水平混凝土支持。基坑围护结构等效为地下连续墙，深度为22 m。地下通道距基坑开挖面最近处18 m，地下通道衬砌结构厚度为1 m。

修正剑桥模型从理论和试验中都较好阐述了土体的弹塑性变形特性，是应用最为广泛的软土本构模型之一[17]。本文土体选用修正剑桥模型，需与多孔介质弹性模型联合使用，具体参数选取如表1所示，上海地区围护结构(地下连续墙)一般采用C30混凝土，其弹性模量为3×107kPa。则基坑围护结构的线弹性模型的弹性模型为 kPa，泊松比为0.2，密度为2 550 kg/m3。

表1 ABAQUS土体本构模型参数

地下通道外墙采用线弹性模型，上海地区一般选用C30混凝土，其弹性模量为3×107kPa。考虑钢筋对其抗拉强度的加强以及忽略地下通道上覆土对其影响，故弹性模型为3×108kPa，泊松比为0.2，密度为2 550 kg/m3。

3.1 基坑不同开挖工况影响分析

考虑基坑开挖过程对邻近地下通道变形影响，结合实际开挖工况及初始应力状态，本文共分为5个施工步骤，计算工况如表2所示。

表2 计算工况表

根据《上海市基坑工程技术规范》[13]对基坑周边环境条件的不同给出了基坑变形设计控制指标，基坑围护结构(钻孔灌注桩)变形和坑外地表沉降作为基坑工程的变形控制指标，对基坑的结构安全和施工安全会产生重大影响，因此对土体分步开挖过程对基坑围护结构(钻孔灌注桩)变形和坑外地表沉降影响进行研究，如图13、图14所示。

图10中，每一级基坑开挖过程中，钻孔灌注桩(图2中AB段)变形的最大值均出现在开挖位置坑底附近。其中第1级基坑开挖变形最大值在开挖深度1 m附近，最大值约为4 mm；第2级基坑开挖变形最大值在开挖深度5 m附近，最大值约为11 mm；第3级基坑开挖变形最大值在开挖深度9 m附近，最大值约为15 mm；整个基坑开挖结束时，钻孔灌注桩最大水平变形值为32 mm左右，位于基坑坑底位置附近(开挖深度12 m附近)，这与图4围护结构对称面(y=0)变形相一致。第3、4级基坑开挖过程中，钻孔灌注桩支撑位置变形相比第1、2级基坑开挖时减小，则是由于基坑水平向支撑对基坑围护结构变形减小的缘故。

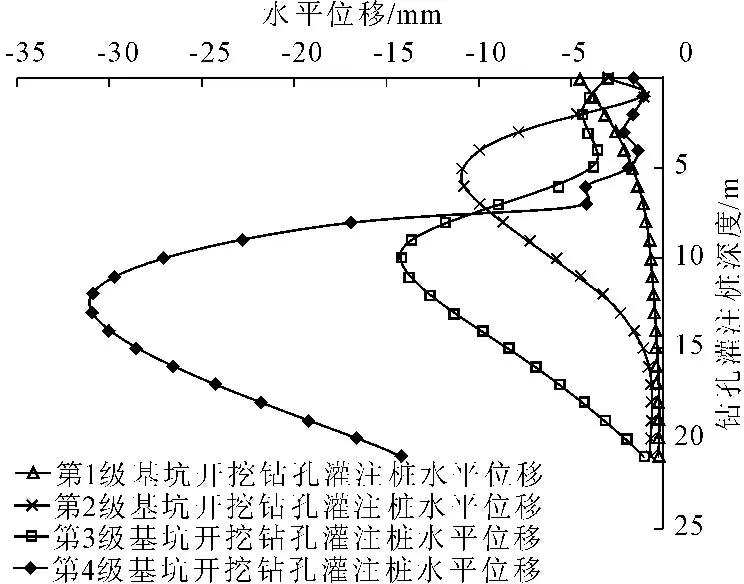
图10不同开挖工况钻孔灌注桩水平位移图

图11中，每一级基坑开挖过程中，地表沉降最大值均出现在距基坑开挖位置为每一级开挖深度附近，其中第1、2、3、4级基坑开挖引起的坑外地表最大沉降值分别为2 mm、6 mm、13 mm、21 mm。其中，第4级开挖引起的地表沉降值和变形规律与理论分析的图5中地表对称面(y=0)相一致。随着基坑开挖深度的增加，坑外地表沉降值变大，且坑外地表最大沉降值的位置随着开挖深度的增加而右移。每一级基坑开挖导致的坑外地表沉降规律基本一致，且沉降量随着开挖深度的增加而增大。

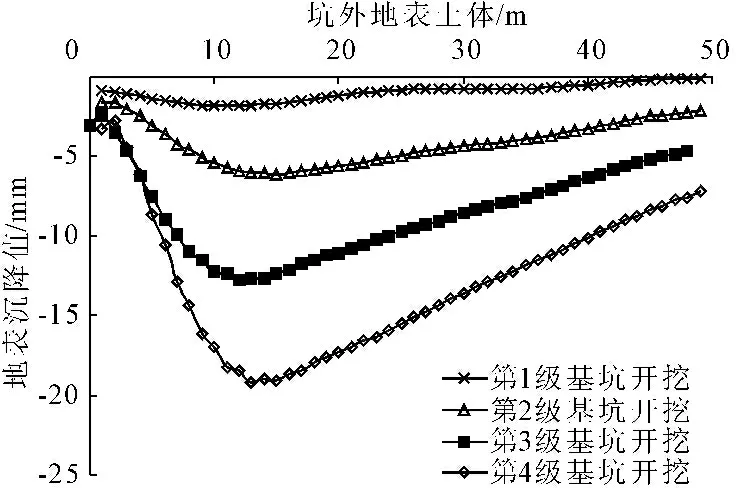
图11不同开挖工况坑外地表沉降图

3.2 基坑开挖不同深度对矩形地下通道变形影响

考虑基坑开挖深度对地下通道变形影响，结合本工程实际工况，以分级开挖深度对地下通道变形影响进行研究，其不同深度选取如表4所示，分别对地下通道底部和左侧地道进行研究分析，如图12、图13所示。

图12中，随着开挖深度的增加，地道底部沉降值随之增大，且地道底部最大沉降值逐渐向地道近基坑一端靠近。第1级基坑开挖地道底部最大沉降值在距离左侧3 m位置附近，最大沉降值约为0.8 mm；第2级基坑开挖地道底部最大沉降值在距离左侧7 m位置附近，最大沉降值约为1.3 mm；第3级基坑开挖地道底部最大沉降值在距离左侧6 m位置附近，最大沉降值约为3 mm；第4级基坑开挖地道底部最大沉降值在最左侧位置附近，最大沉降值约为4.6 mm。通过与理论值对比可知，有限元计算值比理论方法值偏大，这是由于有限元方法考虑了土体重力作用。由此可知整个基坑开挖过程中最大沉降值均小于5 mm，满足设计要求。

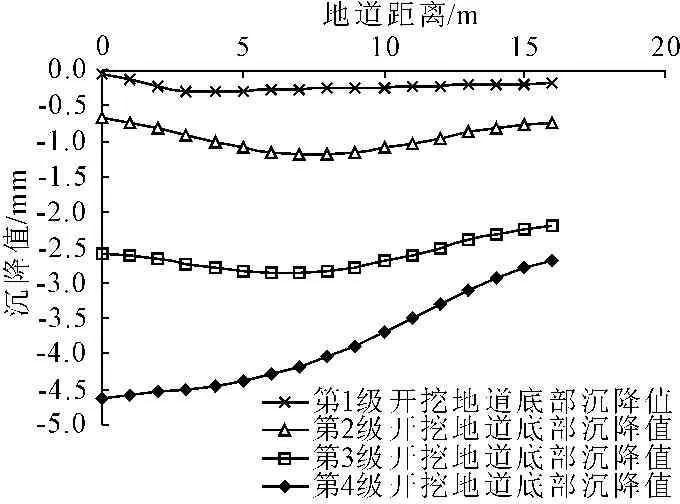
图12不同开挖深度下地道底部竖向变形图

图13中，随着开挖深度的增加，左侧地道水平位移随之增大，且最大水平位移值均出现在左侧地道上部位置。不同开挖深度下的左侧地道水平位移曲线基本呈现线性规律，在开挖深度较浅时，左侧地道水平位移呈现出整体变形规律，随着开挖深度的增加，左侧地道上部位置水平位移增加速率大于下部位置水平位移。第1级基坑开挖由于开挖深度只有1 m，对左侧地道水平位移的影响可以忽略不计，其中出现部分位置向右变形，则是由于初始地应力平衡量级与左侧地道水平位移值的量级相近造成的；第2级基坑开挖左侧地道水平位移最大值在左侧地道顶部，约为0.8 mm，且整个左侧地道水平位移值基本相同；第3级基坑开挖左侧地道水平位移最大值在左侧地道顶部，约为1.8 mm；第4级基坑开挖左侧地道水平位移最大值在左侧地道顶部，约为3.7 mm。其中，左侧地道水平位移的最终值和变形规律与理论方法的图8相一致。由此可知整个基坑开挖过程中左侧地道最大水平位移值均小于5 mm，满足设计要求。

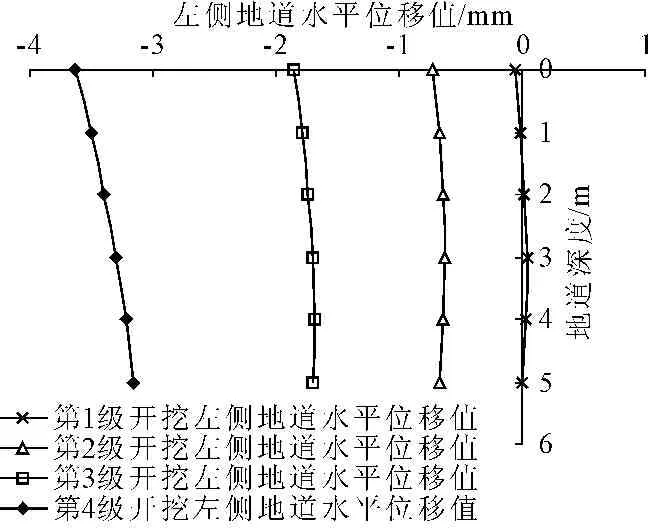
图13不同开挖深度下左侧地道水平位移图

4 结 论

本文以某深基坑开挖邻近上海市中环线既有矩形地下通道工程为背景，分析深基坑开挖效应导致的邻近地下通道结构变形的影响，将二阶段法应用于基坑开挖对邻近矩形式地下通道结构变形研究。求解基坑开挖对邻近地下通道变形的理论解答，采用弹性地基梁理论对地下通道的变形和受力机理进行讨论，推导出地下通道地基梁计算方法，预估基坑开挖效应导致的邻近地下通道结构变形及附加应力，根据相应预估值对基坑施工采取相应措施，得出相关结论。是对基坑开挖对邻近地下通道变形控制标准的具体补充，为建立软土地区深基坑开挖效应的评价体系提供科学参考，为实现深基坑开挖的安全施工、地下通道的安全运营、为类似工程施工提供理论参考。