基于声发射技术的钢纤维混凝土受压损伤本构关系研究

黄 彪， 李 彪

(武汉大学 土木建筑工程学院， 湖北 武汉 430072)

近年来，钢纤维混凝土以其优越的力学性能，被广泛应用于工程建设中[1]。当钢纤维均匀加入混凝土基体中，混凝土中形成多向约束系统，能显著提高混凝土抗拉、抗剪强度，改善其韧性和延性。姬小祥等[2]对铣削型、端钩型和压痕型三种类型钢纤维混凝土的力学性能进行了分析。韩嵘等[3]、杨萌等[4]对钢纤维混凝土受拉应力-应变关系曲线进行了研究，并得到了钢纤维混凝土受拉应力-应变全曲线的数学模型；高丹盈[5]、张晓燕等[6]、Bencardino F等[7]对钢纤维混凝土受压力学行为进行研究，并对试验数据进行拟合得到了受压应力-应变全曲线的数学表达式。邓宗成等[8]对SFRC进行反复加卸载试验，建立了钢纤维混凝土反复加卸载应力-应变曲线方程及变形计算公式。董毓利等[9]基于不可逆热力学理论提出了含损伤的弹塑性内时本构模型，并与试验结果吻合良好。宋玉普等[10]在普通混凝土内时损伤本构模型的基础上，引入纤维参数对损伤变量的影响，建立了SFRC内时损伤本构模型。王春来等[11]和宁喜亮等[12]根据Weibull统计分布理论和等效应变假定原理得到SFRC的损伤本构模型，并基于实验数据对模型的参数进行了拟合。

综上可知，国内外学者对钢纤维混凝土力学行为和本构关系开展了大量研究，取得了重要成果，对钢纤维混凝土的工程应用和发展具有重要作用。但仍存在以下问题：(1) 目前对钢纤维混凝土的研究仍停留在宏观层次，纤维细观桥接作用和滑移机制并未得到很好的揭示；(2) 钢纤维混凝土破坏过程以及混凝土内部微裂纹扩展和损伤演化过程研究较少；(3) 钢纤维混凝土损伤本构关系研究还较少。

声发射是材料变形、裂纹开裂及扩展过程的伴生现象[13-18]，并且声发射过程与力学过程密切相关。通过测量和分析钢纤维混凝土在受力过程中发出的声发射信号，可推断结构内部的破坏，并识别损伤的大小。严伟洋等[19]对各应力水平下斜长花岗岩的声发射事件活动规律进行了研究，结果表明声发射事件累计计数可以很好描述岩石受压破坏的全过程。Ohstu M等[20-21]采用声发射撞击数和声发射信号幅值对混凝土结构的损伤程度进行评估。Grosse C等[22]和Mclaskey G C[23]等考虑不同声发射信号达到时间不同对混凝土结构中的损伤进行定位。Finck F等[24]和Ohstu M等[25]利用声发射对混凝土的破坏机理进行了研究，可以通过声发射信号区分混凝土的破坏模式。

本文在国家自然科学基金(51478367，51608397)的资助下，通过钢纤维混凝土单轴受压试验，并采用声发射系统同步采集加载过程中的声发射信号，深入分析了纤维对混凝土力学行为以及声发射参数的影响，基于试验数据，建立了钢纤维混凝土单轴受压本构关系方程。

1 试验概况

1.1 原材料与配合比

根据《普通混凝土配合比设计规程》[26](JGJ 55—2011)和《纤维混凝土结构技术规程》[27](CECS38：2004)设计C40混凝土。钢纤维混凝土的材料为：P.O 42.5普通硅酸盐水泥；碎石(粒径为5 mm～25 mm)；河砂(细度模数为2.7)；聚羧酸高效减水剂(减水率20%)。钢纤维的物理力学性能见表1，混凝土基体配合比见表2。

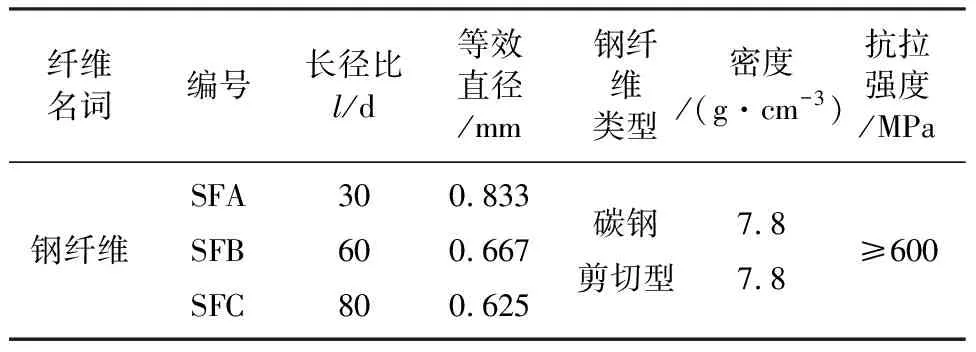
表1 钢纤维物理力学性能

表2 混凝土基体配合比

1.2 试件制作与养护

参考课题组前期研究成果和相关规程建议，确定试验中钢纤维体积掺量为1.0%、1.5%、2.0%，长径比为30、60、80。共设计6组18个钢纤维混凝土试件，包括5组钢纤维混凝土试件和一组普通混凝土试件。试件主要参数见表3。

本文试验采用棱柱体试件，试件的尺寸为150 mm×150 mm×300 mm。参考《钢纤维混凝土试验方法》[28](CECS 13—1989)进行本文试验试件的制备。试件浇筑时，同批次制作6个边长为150 mm的立方体试块，28 d龄期后，按《普通混凝土力学性能试验方法标准》[29](GB/T 50081—2002)测试其立方体抗压强度和劈裂抗拉强度，试验结果见表3。

表3 钢纤维混凝土的力学性能

1.3 试验装置及加载制度

试验测试系统由电液伺服岩石力学测试系统INSTRON 1346和PCI-2声发射信号采集系统组成。试件加载在INSTRON1346万能试验机上进行。测试过程中，在试件高度方向上布置一个量程为5 mm的电子位移计，用于量测试件在加载过程中产生轴向变形；在横向方向上布置两个量程为2.5 mm的电子位移计，用于量测试件在加载过程中产生的横向变形。

试验中采用2个声发射探头(Nano30)对声发射信号进行采集，探头频率分布为100 kHZ～400 kHz，幅值范围为0～100 dB。试验过程中记录的声发射参数有：通道号、到达时间、幅值、持续时间、上升时间、振铃计数、上升计数、能量和撞击数等。

本试验参照《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)[29]实施，加载过程中采用位移控制加载方式，加载速度为0.005 mm/s，直至试件破坏。

2 试验结果及分析

2.1 破坏过程与破坏形态

图1为各试件破坏形态。

图1各试件破坏形态

试验结果表明，普通混凝土的破坏为脆性破坏。试件破坏时主裂纹较宽，界面清晰，细裂纹少，开展速度快，在加载过程中试件突然断裂。加载初期，试件只发生弹性变形，随着荷载增加，竖向微裂纹出现，荷载继续增加，裂纹不断扩展，最后形成贯通裂缝，试件破坏。对于钢纤维混凝土试件，加载过程中出现的裂纹细而多，发展缓慢，逐渐延伸，最后试件经过一个裂缝持续缓慢发展的过程后断裂。随着钢纤维体积掺量增加和长径比提高，试件产生的裂缝变细，试件的韧性和延性得到提高。这是因为对于钢纤维混凝土，当试件在荷载作用下基体发生破坏，产生裂纹之后，横跨裂缝两端的钢纤维会形成桥接作用，延缓裂缝的衍生、扩展和连接贯通。桥接在裂缝两端的钢纤维在被拔出的过程中会消耗大量能量，使钢纤维混凝土试件的破坏呈现出延性特征。

2.2 应力-应变全曲线

根据钢纤维混凝土轴心受压荷载-变形全过程曲线，结合在试验过程中对试块破坏形态的观察，将SFRC轴心受压应力-应变曲线分为四个阶段：弹性阶段(OA)、裂缝稳态扩展阶段(AB)、裂缝失稳扩展阶段(BD)以及破坏阶段(D以后)。如图2所示。

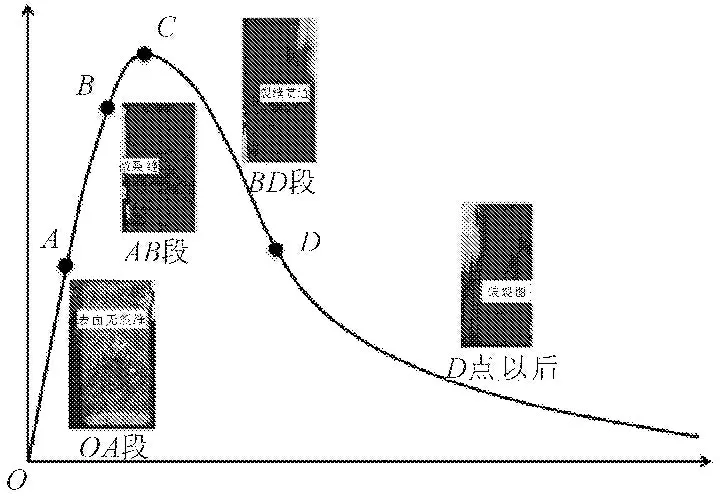
图2典型SFRC轴心受压应力-应变全曲线

图3为典型各混凝土试件轴心受压应力-应变全曲线。与普通混凝土试件相比，钢纤维混凝土试件应力-应变曲线上升段与普通混凝土无太大差别，但下降段曲线比普通混凝土更平缓，表现出更好的韧性和延性。并且随着钢纤维体积掺量增加，试件的韧性和延性提高(见图3(a))。分析原因是：钢纤维在SFRC受压破坏的过程中，通过钢纤维与混凝土基体间的粘结、滑移以及拔出，吸收了大量能量，体积掺量越大，钢纤维拔出滑移需要耗散的能量越多；固定体积掺量，长径比更高的钢纤维混凝土试件应力-应变曲线下降段更平缓，表现出更好的韧性和延性(见图3(b))。分析原因是：长径比更高的钢纤维在混凝土基体中与混凝土锚固时产生的锚固长度更大，拔出过程中需要的拔出力越大，吸收的能量越多。

2.3 基于声发射参数的损伤机理分析

声发射是固体内部的缺陷或潜在缺陷，在外部条件作用下而自动发声。通过布置在材料表面的传感器接收声发射信号，对声发射信号进行分析，便可判断材料的物理状态。由于声发射信号来自材料内部缺陷本身，不同的缺陷会产生不同的声发射信号，因此用声发射法可以判断缺陷的性质。典型声发射波形图见图4。

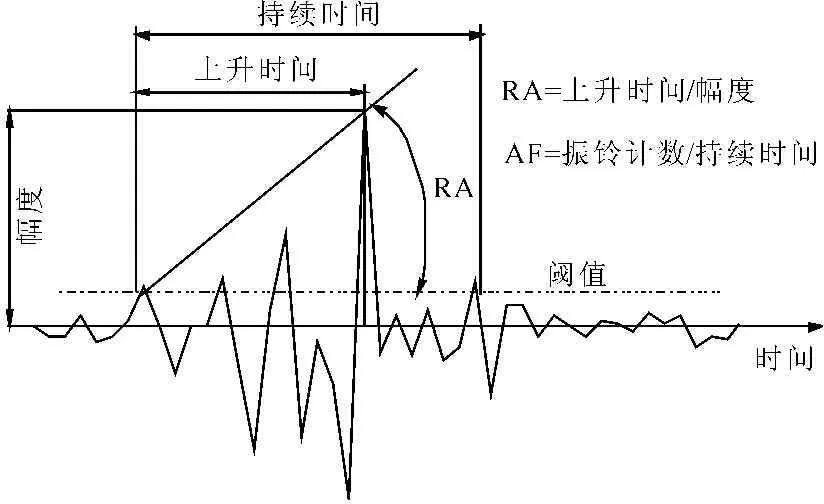
图3 不同SFRC试件轴心受压应力-应变曲线

图4典型的声发射波形图

2.3.1 撞击数

图5反映了试件1在单调加载过程中，力和声发射撞击数与时间的关系。试件2—试件6力和声发射撞击数与时间的关系与试件1相似。据图5分析可知：加载初期，声发射撞击数较少，增长速度缓慢；在出现贯通的斜裂缝(即图5中的D点)之后，声发射撞击数在短时间内突然迅速增加；随后声发射撞击数逐渐趋于平缓。由于声发射是材料在变形或破坏过程中局部能量以应力波释放而产生的现象，因此可根据撞击数随时间的发展过程分析钢纤维混凝土试件内部损伤发展过程。当试件处于弹性阶段以及裂缝发展阶段，破坏大多是由于混凝土基体间裂缝的开展，钢纤维桥接在裂缝之间，延缓裂缝的扩展，因此破坏时释放的能量较少，能量释放率较低；当到达D点时，试件表面形成贯通斜裂缝，并伴随有表面混凝土剥落，桥接在裂缝间的钢纤维受力拉紧，并随着荷载增加不断拔出，处于拉紧状态的钢纤维拔出过程十分短暂，会释放出大量能量，因此声发射撞击数突然显著增加。

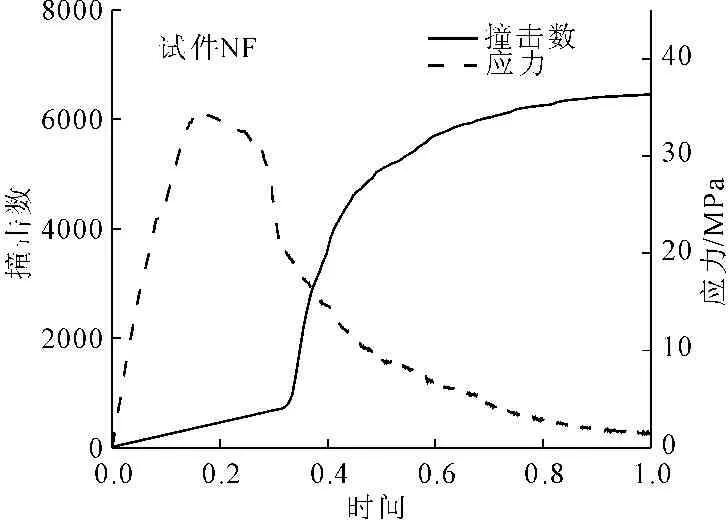
图5试件1的力与声发射撞击数的时间历时

图6为不同试件声发射撞击数与时间的关系曲线。从图中可以看出：

(1) 在加载初期，各个试件无明显区别，且撞击数都增加缓慢。由此可知在加载初期，钢纤维并未发挥作用，荷载由混凝土基体承担，钢纤维混凝土与普通混凝土无明显差别，并且此阶段试件内部微裂缝扩展缓慢，断裂能释放较少，因此撞击数发展较为平缓。

(2) 钢纤维混凝土试件的撞击数突增时间点迟于普通混凝土，这说明钢纤维混凝土贯通裂缝的形成时间晚于普通混凝土。因为钢纤维混凝土开始产生裂纹以后，钢纤维会发挥桥接作用，阻止了裂缝的进一步扩展，使其贯通裂缝的形成要迟于普通混凝土。由此可以看出钢纤维能延缓混凝土裂缝的开展。

图6不同试件声发射撞击数与时间的关系

2.3.2 RA和AF

已有研究[22-23]表明，声发射参数RA(上升角)值和AF(平均频率)的相对关系可以用来区分混凝土不同的破坏模式。RA定义为上升时间和波形幅值的比值的比值，平均频率定义为振铃计数和持续时间的比值。不同的破坏形式会产生不同的波形，受拉破坏会导致材料内部瞬间产生体积变化，内部能量主要以纵波的形式释放，此种波形有更高的幅值、更高的频率以及更快的传播速度，因此上升时间短；当发生剪切破坏时，虽仍有一部分能量以纵波形式释放，但大多数能量仍以横波形式传播，频率更低、速度更慢，因此上升时间更长。故当发生剪切破坏时，AF较低，RA值较高；当发生受拉破坏时，AF较高，RA值较低，如图7所示。

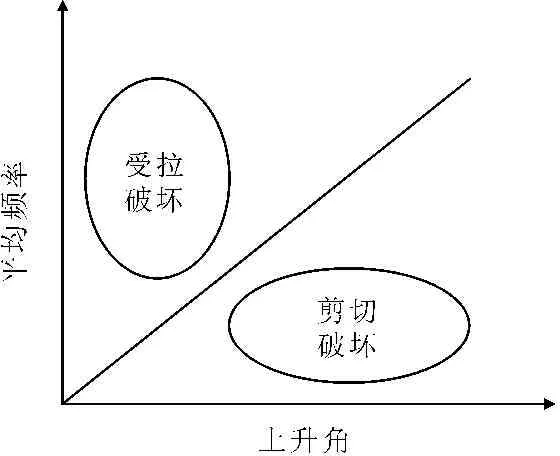
图7破坏模式分类

由各个试件加载过程中声发射参数RA值与AF的关系可知，所有试件的AF值大多分布在0～100 KHz之间，RA值大多分布在0～1 400 ms/V之间，试件的破坏兼顾受拉破坏与剪切破坏。对于普通混凝土，试验点绝大多数集中在图中对角线左上区域，即RA值较小，AF值较大的区域，因此普通混凝土在加载过程中发生的破坏属于受拉破坏，；对于钢纤维混凝土，试验点在右下区域(即RA较大，AF较小的区域)也有大量分布，说明钢纤维混凝土在加载过程中发生的破坏既有受拉破坏，也有剪切破坏。

3 单轴受压损伤本构关系

3.1 损伤理论

(1)

对于完全无损状态，D=0；对于完全丧失承载能力的状态，D=1。

根据Lemaitre提出的应变等价原理，受损材料的本构关系可以通过无损材料的名义应力得到，即

(2)

即

σ=(1-D)Eε

(3)

式中：E为无损伤时的初始弹性模量；ε为应变。

3.2 损伤变量

材料声发射是其内部损伤(微裂隙和微孔洞)产生和发展的结果，与材料的损伤变量、本构关系等之间存在必然联系[30]，因此可以用声发射参数分析损伤演化规律，从而建立材料的损伤本构模型。

考虑一无初始损伤的材料，若整个截面A破坏时累积的声发射振铃计数为Nm，则单位面积微元破坏时的声发射率为

(4)

则当断面破坏(损伤)面积达Ad时，累积的声发射振铃计数为

(5)

由式(1)和式(5)可知，声发射振铃计数与损伤变量之间存在以下关系，即

(6)

对于混凝土、岩石等准脆性材料，损伤演化规律常可采用形状变量如应变ε表示为

(7)

式中：f(ε)为为损伤演化函数；ζ为一可变的损伤应变门槛值。

对于单调加载，假设初始损伤条件为D=ε=ζ=0，并且条件ε>ζ与dε>0总成立，则由式(6)和式(7)可得

(8)

式中：F(ε)为概率分布函数。

对于不同损伤机制，损伤演化函数f(ε)可选择不同形式。宁喜亮等[12]考虑混凝土微元强度服从Weibull分布，张明等[30-31]建议采用对数正态概率密度函数描述准脆性材料微元的损伤演化规律。本文考虑采用对数正态分布来描述混凝土的损伤演化规律，即

(9)

(10)

式中：Φ为标准正态概率分布函数；参数b为尺度参数;ζ为材料的非均匀度。将式(10)代入式(8)，得到

(11)

式(11)中参数b与参数n为未知参数。通过单调受压试验，借助声发射系统可测得钢纤维混凝土试件在受压过程中声发射振铃计数与应变ε之间的对应关系，从而可得到损伤变量D与应变ε之间的关系，试验结果如图8所示。根据式(11)对试验结果进行回归分析，可得参数b与参数n，结果见表4。

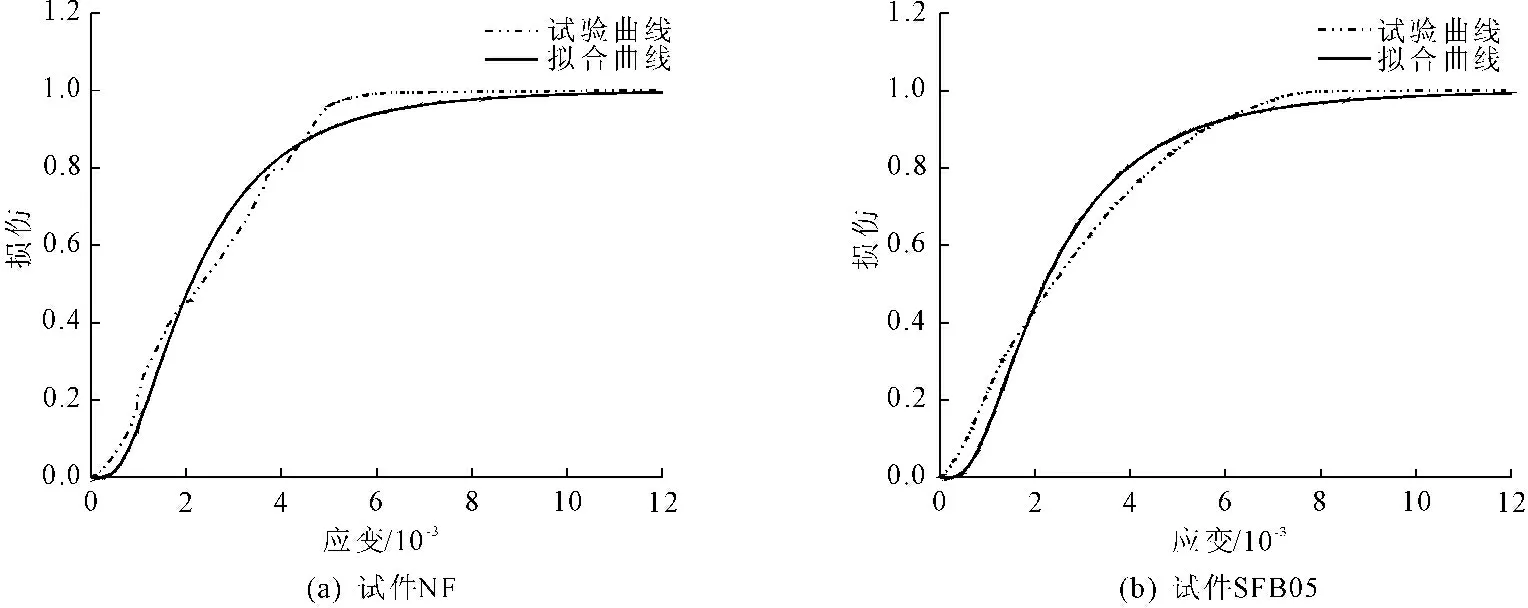
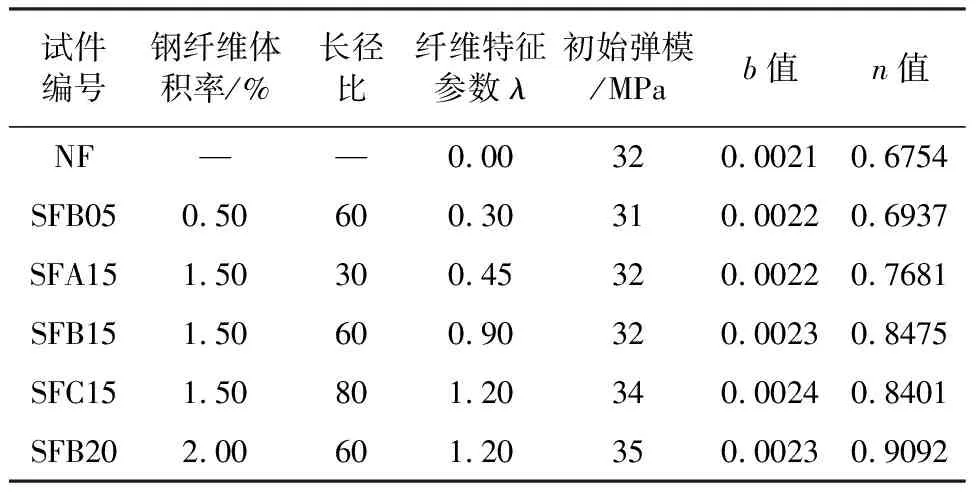
图8 各试件在单轴受压条件下损伤变量与应变的关系

为准确量化钢纤维的影响，引入纤维特征参数λ：

λ=ρl/d

(12)

式中：ρ为钢纤维的体积掺量；l/d为钢纤维的长径比。

(1) 参数b与纤维特征参数λ的关系。上述结果已有不同试件对应的b值，则可得不同纤维特征参数λ对应的b值，其对应关系如图9(a)所示。

对试验数据进行拟合，可得参数b与纤维特征参数λ之间的关系：

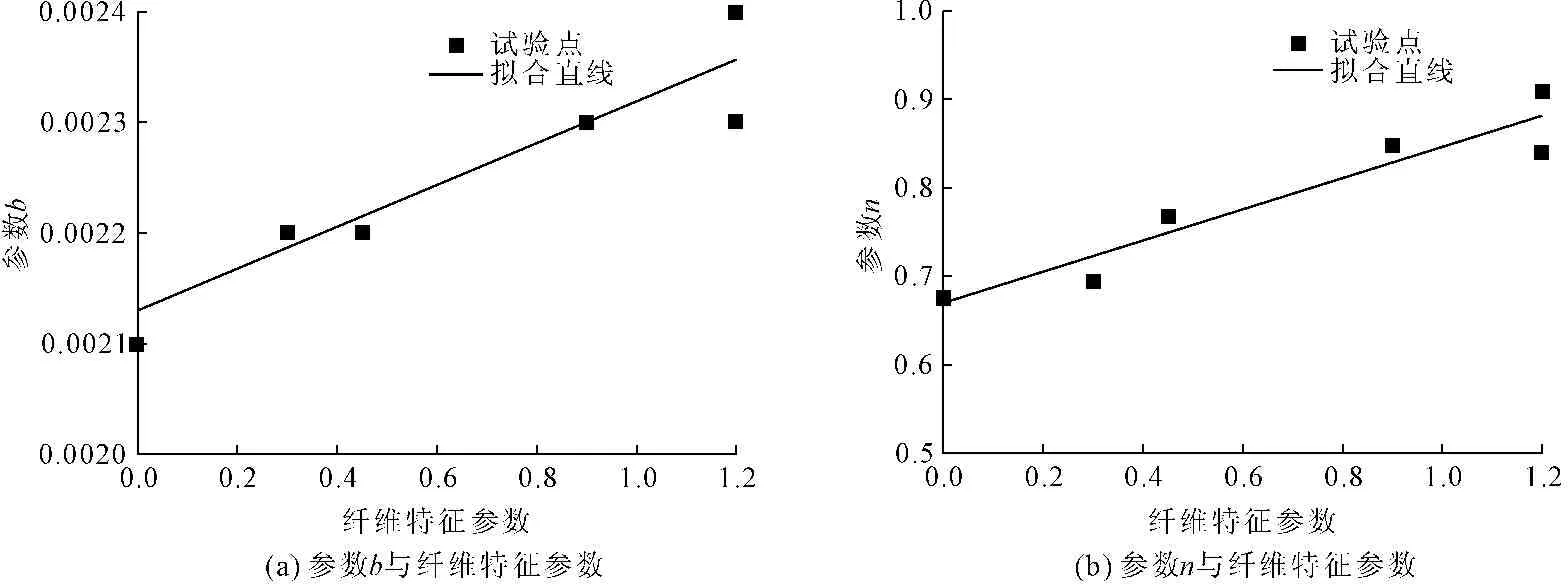
b=0.000189λ+0.00213 (13)

图9纤维特征值对损伤本构关系的影响

(2) 参数n与纤维特征参数的关系。根据上述结果可得不同纤维特征参数λ对应的n值，其对应关系如图9(b)所示。对试验数据进行拟合，可得参数n与纤维特征参数λ之间的关系为：

n=0.17635λ+0.66996

(14)

将式(13)、式(14)代入式(11)中可得含纤维特征参数λ的钢纤维混凝土的损伤变量表达式

(15)

3.3 本构方程

将上述式(15)的结果代入式(3)，可得

(16)

上式即为采用对数概率密度函数作为损伤演化函数得到的钢纤维混凝土单轴受压损伤本构方程。式中，E为钢纤维混凝土各试件初始弹性模量。

3.4 模型验证

选取曲线原点到30%～40%极限强度点直线段的斜率为初始弹性模量[32]，计算结果见表4。将表4中的参数代入式(16)，即可得损伤本构方程表示的理论曲线。

为了验证上述提出的损伤本构方程的普适性，本文采用文献[11]中钢纤维混凝土的试验参数代入式(16)，将根据模型得到应力-应变曲线绘于图10中，将模型曲线与试验测得的应力-应曲线进行对比。可以看出，建立的模型能很好地预测钢纤维混凝土的应力-应变曲线。

图10宁喜亮钢纤维混凝土试件试验曲线与理论曲线对比

4 结 论

(1) 钢纤维具有提高混凝土峰值强度，阻止裂缝开展的作用；钢纤维混凝土破坏呈现明显的延性特征。

(2) 钢纤维体积掺量和长径比会影响SFRC单轴受压力学行为。体现在：① 钢纤维的掺入会提高试件的峰值强度和峰值应变；② 长径比相同，体积掺量越高，试件的峰值强度和峰值应变越高，延性和韧性越好；③ 体积掺量相同，长径比越大，试件的峰值强度和峰值应变越高，延性和韧性越好。

(3) 可以用声发射反映试件破坏过程和区分材料的破坏形式。在贯通裂缝形成前，材料释放的能力较少，声发射撞击数增加缓慢，形成贯通裂缝时，材料释放大量能量，声发射撞击数突然显著增加；当材料发生受拉破坏时，声发射RA值较小，AF值较大；当材料发生剪切破坏时，声发射RA值较大，AF值较小。

(4) 基于试验数据，以对数正态分布函数作为损伤演化函数，提出了SFRC单轴受压损伤本构模型，可为钢纤维混凝土工程应用和相关规程的修订提供参考。