不同端距下的螺栓连接板承载性能分析

徐忠根，肖德俊，邓长根，陈荣毅

(1.广州大学 土木工程学院, 广东 广州 510006； 2.广东省复杂钢结构工程技术研究中心， 广东 广州 510006；3.同济大学 土木工程学院, 上海 200092； 4.广州南沙明珠湾起步区开发建设指挥部， 广东 广州 511455)

在钢结构设计中，螺栓作为一种重要的连接方式，得到了迅速的发展，广泛地运用于建筑、机械、汽车等领域。国内外学者就普通螺栓和高强度螺栓连接的构件的承载性能，作了广泛的研究[1-8]。结果表明：板件的承压性能与端距和螺栓孔径的比值e/d0、螺栓直径d、板厚t等因素相关。针对螺栓端距e，即构件边缘沿受力方向到第一排螺栓孔中心的距离，《钢结构设计规范》[9](GB 50017—2017)作出了明确的规定，要求最小的容许距离为2d0，最大的容许距离在4d0和8t中取较小值。在德国规范[10]中，针对端距取值的要求：最小的容许距离为1.2d0，最大的容许距离取3d0和6t中的较小值。对比两国规范，发现有一定的差异。因此本文从端距着手，选择螺栓双受剪面剪切连接板进行分析。

1 计算模型方案

本文通过有限元软件ABAQUS建立螺栓双剪切连接板模型，分析端距e对于连接板承载性能的影响。如图1所示，模型主要由盖板、连接板和螺栓组成。盖板的外形尺寸为300 mm×154 mm×7 mm，连接板的外形尺寸为770 mm×154 mm×10 mm，螺栓型号为8.8级M20，孔径d0为22 mm。

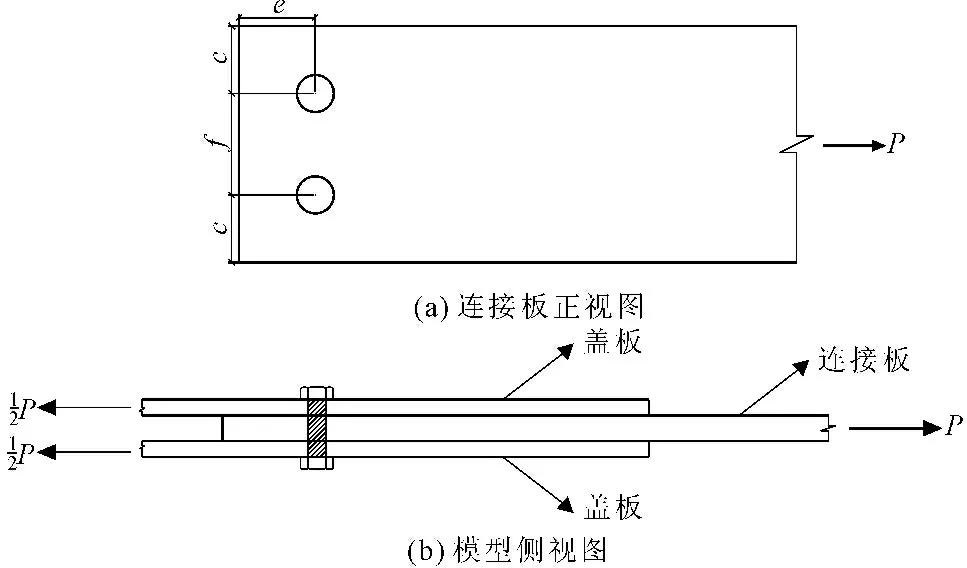
图1螺栓连接板模型

1.1 网格划分和单元属性选取

连接板是力学性能分析的重点部分。在划分网格时，考虑到螺栓孔及其附近区域存在应力集中，并且变形较大，故进行了局部加密，提高计算结果的精度。因此，模型中的盖板、连接板和螺栓均采用C3D8I单元[11-14]，以保证在较短的时间内得到较精确的位移结果。该单元的形函数阶数较高，所以要求的单元控制点和高斯积分点的数量都较多，提高了计算精度。八结点单元的形函数表示为：

(1)

其中，ξ0=ξiξ；

η0=ηiη；

ζ0=ζiζ(i=1,2,…8)

单元内任意一点处的位移d、应变ε和应力σ可以按照下式求出：

d=Nδe

(2)

ε=Bδe

(3)

σ=DBδe

(4)

由虚功原理可知，对于由相互接触的物体所组成的平衡系统，单元的外力虚功和内力虚功是相等的，因此得到单元刚度方程：

F=Kδe

(5)

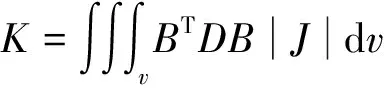
在上式中，d是单元中任意一点的位移向量，N是形函数矩阵，由坐标函数组成，δe是单元结点位移向量，B是应变向量，D是弹性向量，J是雅可比向量。

建立模型时，定义螺栓和连接板间的接触单元为：沿接触面法线方向为硬接触，切线方向则为库仑摩擦接触，摩擦系数为0.35[15]。主要包括以下三个方面：连接板和盖板接触、螺栓和盖板上表面接触、螺栓杆和盖板、连接板孔壁接触。当两个接触表面的间隙为零时，即施加接触约束，接触压力在两表面间传递。

1.2 本构关系

本文试件选择承压型8.8级螺栓，规格为M20，保证施加荷载时不被提前剪断。板件为Q345级钢。根据规范要求，材料的弹性模量E=2.06×105MPa，泊松比都为0.3。板件和螺栓材料不同，本构关系如图2所示。

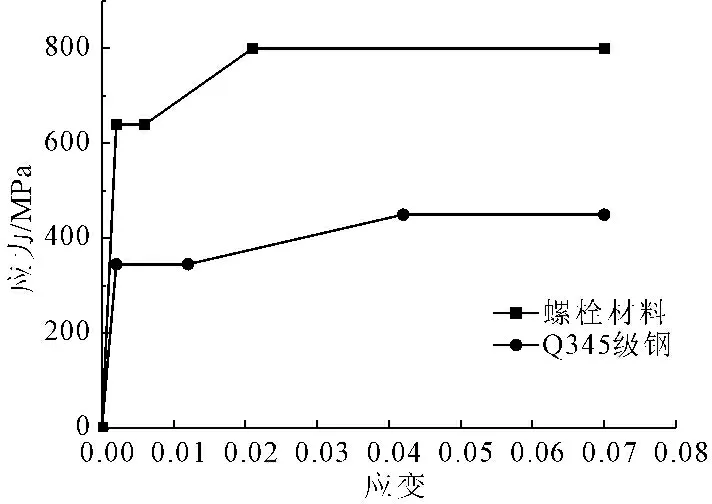
图2本构模型

1.3 约束和荷载的施加

建立有限元模型时，在添加约束和荷载部分，本文根据实际情况，在上、下两块盖板的左端施加沿x、y、z三个方向的约束，连接板的右端逐步施加水平的位移荷载，加载量为20 mm，进行计算和受力分析。

在中、德两国的规范中，关于螺栓连接端距，最小和最大的容许距离都有一定的差异。因此本文选取了1.0d0、1.2d0、1.4d0、1.6d0、1.8d0、2.0d0、3.0d0和4.0d0八个参数，并且根据连接板厚度的不同分为SJ1和SJ2两组，对其承载性能进行对比分析。边距c和线距d的取值满足中国规范最小容许距离的要求，分别为44 mm和66 mm。

2 有限元结果分析

本文利用上述有限元建模的方法，建立了SJ1和SJ2两组模型，对连接板的承载性能、螺栓孔内壁的应力分布等情况进行了分析。

2.1 荷载-位移曲线

在实际工作中，连接板可能存在多种破坏形式：板件承压破坏、板件拉坏和板件端部破坏等。本文主要分析其承压破坏，包括两种形态：(1) 当端距较小时，可能发生螺栓从端部撕裂；(2) 当端距较大时，螺栓孔发生塑性变形被拉长。中国规范提出关于端距的最小容许距离的要求，就是为了避免第(1)类破坏形式。

如图3所示，当连接板的厚度为10 mm时，不同端距下的荷载-位移曲线表现出了相同的变化趋势。

图3 10 mm板厚下不同端距的荷载-位移曲线

在加载初期，随着荷载的增大，螺栓与孔壁接触，发生应力集中，连接板很快进入塑性阶段。荷载-位移曲线出现弯折点，并且有较长的屈服平台，表现出良好的延性。随着端距的增大，屈服荷载、极限承载力都不断地增大。

2.2 极限承载力

表1为当连接板的厚度为10 mm时，在不同端距的取值条件下，屈服荷载、极限承载力、发生屈服时的变形量Δ1和达到极限状态的变形量Δ2的对比。

从表1中可以发现，当端距为1.0d0时，屈服荷载为170.18 kN，极限承载力为241.37 kN，变形量Δ1和Δ2分别为2.11 mm和10.95 mm。随着端距的增大，极限承载力和变形都增大。当端距为1.2d0时，屈服荷载和极限承载力分别是228.17 kN和289.25 kN，变形量Δ2为12.42 mm，同端距为1.0d0的情况作比较，三个值分别提高了34.13%、19.81%和13.42%。

表1 10 mm板厚试件参数对比

当端距为1.8d0时，屈服荷载为322.52 kN，极限承载力为377.75 kN。对比端距为2.0d0的情况，屈服荷载和极限承载力分别提高了4.51%和3.43%。再将端距取值分别为3.0d0和4.0d0的情况作对比：屈服荷载和极限承载力分别提高0.72%和0.41%。此时，端距的变化对连接板承载性能的影响较小。

为了更加直观地表现端距的变化对连接板极限承载力产生的影响，将端距作为x轴，极限承载力作为y轴，绘出变化规律曲线如图4所示。

当连接板厚度为8 mm时，随着端距的增大，屈服荷载和极限承载力也增大。对比端距为1.8d0和2.0d0的试件，屈服荷载和极限承载力分别提高4.78%和2.13%。当端距为3.0d0和4.0d0时，分别提高了为3.77%和2.01%。同样地，当端距取值在1.8d0和2.0d0，以及3.0d0和4.0d0间的时候，增大端距，对极限承载力影响较小。

图4不同端距下极限承载力的对比

通过以上的分析，由图4可以看出：在8 mm和10 mm两种板厚条件下，端距e都会对连接板的极限承载力产生影响。同种板厚时，随着端距的增大，极限承载力也在不断增大。并且，当端距取值范围在1.0d0≤e≤1.8d0时，极限承载力增长速度较快；当端距取值为1.8d0≤e≤4.0d0时，增长速度呈减小的趋势。

2.3 螺栓孔内壁应力

对于每个试件，上、下盖板左端和连接板右端的应力都小于螺栓孔内壁的应力。因为应力集中和破坏点的位置都在螺栓孔及其附近区域。

为明确螺栓孔内壁应力的发展和分布情况，以在10 mm连接板厚度的条件下，端距为2d0的试件为例，取其连接板上的1号螺栓孔进行具体分析。如图5所示，以轴向拉力N的方向作为正向起点A，按照90°的间隔依次取点B、C、D。

图5螺栓孔内壁应力分析示意图

如表2所示，当荷载由150 kN增大到350 kN的时候，连接板上1号螺栓孔内壁的周向应力逐渐增大，变形也逐渐增大。在加载初期，主要是连接板端部承受力的作用。当加载荷载从250 kN变化到350 kN时，试件开始进入塑性阶段，应力值增大，同时水平位移也表现出较大的增长幅度，螺栓孔内壁的C点及其附近区域出现明显的应力集中。此时试件承受荷载的主要部位是螺栓孔内壁及其附近区域，螺栓孔被拉长，产生塑性变形。

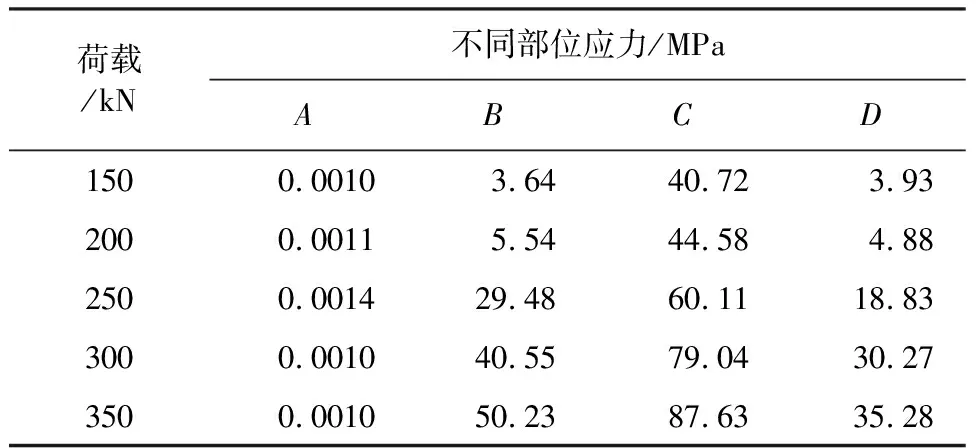
表2 螺栓孔内应力分布

注：螺栓杆与孔壁在A点未发生接触。

2.4 端距对螺栓孔内壁应力的影响

由上文可知，C点及其附近区域是螺栓连接应力集中及破坏位置所在。因此取端距为1.8d0和2.0d0的两组试件，分析端距的变化对其连接板上1号螺栓孔的C点及其附近区域的应力分布产生的影响。

以端距为1.8d0和2.0d0的试件为例，对比分析其连接板上1号螺栓孔的受力过程，以及孔壁及其附近区域的应力发展和分布情况，可以得出随着外加荷载的增大，螺栓孔变形逐渐增大，周向应力逐渐增大，表现出应力集中。并且在B～C点的范围内应力较大，是发生破坏的位置。当端距取值为1.8d0时，能够承担较大的应力，并且表现出良好的延性。

当连接板发生破坏时，螺栓产生最大应力的位置在与孔壁发生接触的螺杆上，而连接板则是螺栓孔内壁受压一侧。当端距取值为1.0d0时，螺栓孔的变形、孔壁的应力集中程度都较严重，可能发生从端部撕裂破坏。随着端距的增大(e1≥1.2d0)，螺栓孔的变形逐渐减小，试件发生孔壁承压破坏。

3 双列螺栓连接板有限元分析

在实际应用中，多列螺栓连接也是一种常用的形式。下面以双列螺栓连接板为例，按照上面的建模方法建立有限元模型，对其承载性能进行分析。

在模型尺寸的选取上，上、下两块盖板的厚度为10 mm，连接板厚度为18 mm。螺栓采用8.8级M20。本节主要讨论双列螺栓连接板模型的受力情况和应力分布。

3.1 荷载-位移曲线

当连接板厚度为18 mm时，比较第三组试件SJ3在1.0d0、1.2d0、1.4d0、1.6d0、1.8d0、2.0d0、3.0d0和4.0d0不同端距下的荷载-位移曲线(见图6)，发现它们具有相同的走向。施加外部荷载后，试件迅速地进入屈服阶段。连接板右端的螺栓孔位置先发生变形，螺栓杆与孔内壁C点产生接触。随着荷载的逐步增大，接触范围从C点向其附近区域扩展，螺栓孔的变形越加明显，直至发生破坏。

图6 18 mm板厚下不同端距的荷载-位移曲线

3.2 端距对承载性能的影响

通过对图6进行分析，可以看到当端距为1.2d0时，极限承载力是863.22 kN，变形值Δ2是16.28 mm；当端距为2.0d0时，极限承载力是876.91 kN，变形值Δ2是14.53 mm。不同端距下的极限承载力和变形值分别相差1.51%和12.04%。因此，当试件按照双列螺栓的形式进行布置时，端距从1.2d0提高到中国规范要求的2.0d0，极限承载力的增长是很小的。螺栓孔变形减小，连接板的延性明显下降。经过综合考虑，此时按照德国规范，端距取值为1.2d0能够较好地满足受力性能的要求。

同理，当端距为3.0d0和4.0d0时，比较两者的荷载-位移曲线，可以看到极限承载力相差1.2%。当端距为4.0d0时，可能发生连接板端部板材翘起的现象，影响受力性能，应当避免。因此端距为3.0d0的试件能够更好地承受荷载，保证试件正常工作。

4 设计方法对比

本节对比了中国和德国规范关于螺栓连接板承压设计值的计算公式。中国钢结构设计规范未提出计算公式，而是以构造措施保证强度，即对端距的容许距离进行了规定：2.0d0≤e≤4.0d0。德国规范对其的规定为1.2d0≤e≤3.0d0，并且提供了设计公式。其中充分地考虑了端距等几何参数对板件承压设计值的影响，与有限元分析结果吻合良好，证明了有限元分析的合理性。

在螺栓双剪切面剪切连接板模型中，与端距为2.0d0时的情况对比，当e=1.2d0时，单列螺栓板件的承载力达到2.0d0时的74.36%，双列螺栓板件的承载力达到2.0d0时的97.02%。故建议螺栓连接构件的端距可以放宽到1.2d0的范围内，但其承载力应适当降低。

5 结 论

针对中、德两国钢结构规范中关于螺栓端距最小和最大的容许距离规定的差异，本文建立有限元模型，对其承载力、应力分布等方面进行了分析，得到结论如下：

(1) 中国规范规定，端距最小容许距离为2.0d0，最大容许距离为4.0d0和8t中的较小值；德国要求端距的最小容许距离为1.2d0，最大容许距离为3.0d0和6t中的较小值。两国规范中关于端距的容许距离取值的要求有一定的差异。

(2) 针对螺栓端距最小的容许距离，通过有限元分析，并且对比中国和德国规范对于螺栓连接板承压设计值的计算公式，可以得到，与端距为2.0d0时的情况比较，当e=1.2d0时，单列和双列螺栓板件的承载力分别达到2.0d0时的81.45%和97.02%。故建议螺栓连接构件的端距可以放宽到1.2d0的范围内，但其承载力应适当降低。

(3) 关于螺栓端距最大的容许距离，试件在端距分别为3.0d0和4.0d0的情况下，极限承载力分别相差1.21%(单列)和2.35%(双列)，因此建议在3.0d0≤e≤4.0d0的范围内，可以适当降低端距最大容许距离的取值。