基于MPC的可变相序交通信号优化控制方法

杨利红，王列伟

(中国电子科技集团公司第三十八研究所 合肥公共安全技术研究院，安徽 合肥 230000)

0 引 言

由路段、交叉口、部署在交叉口的交通信号灯，以及车辆和人的动态行为组成的城市道路交通网络系统可以被看成一类含有大量不确定性的复杂的离散事件系统。而城市道路交叉口信号系统的设计与优化是提高城市道路利用率、减少拥堵的关键。文中研究了基于Petri网的道路交叉口信号控制系统的建模及优化方法。

Petri网是一种常见的离散事件系统模型[1]。Petri网模型对动态系统中常见的并行(parallelism)、同步(synchronization)、资源共享(resource sharing)等特性具备强大表述能力，广泛应用于工业制造系统、软件系统设计、工作流、并行计算、交通系统等领域。近年来，使用Petri网对道路交叉口系统进行建模的方法受到学者的广泛关注，具有代表性的成果见文献[2-8]。其中文献[2-5]建立基于Petri网的微观交通模型，通过时延Petri网、随机Petri网、着色Petri网等结构，描述交叉口信号灯色的切换、车辆在道路上的移动速度以及车辆在交叉口内可能的转向和路径选择等信息。系统仿真证明，通过这类模型可以较准确地计算出车辆排队长度以及车辆在交叉口的平均等待时间。文献[6-8]不以单个车辆作为建模对象，而是类似于连续时间系统(continuous-time system)，主要以交通流量、车辆速度，以及车辆密度等作为描述对象，建立基于混合网结构的宏观交通模型。然而，上述这些交叉口建模及优化算法都是基于传统的交通信号固定相序逻辑，没有充分考虑车流到达的随机性、突发性等不规律的动态特征，优化空间有限。在文献[9-10]中，作者虽然考虑了基于可变相序的优化算法，但是优化函数大都是根据当前或者历史数据构造(例如通过当前的车辆排队长度、车辆停留时间、车辆通过时间等)，而没有考虑系统状态的预测，对车流实时状态的适应性有待提高。

文中首先建立了基于混合Petri网的可变相序交通信号模型，并创新性地提出了一种基于MPC(model predictive control，模型预测控制)[11-12]的优化控制算法。根据MPC控制模型，该算法在每一个采样瞬间通过求解一个有限时域开环最优控制问题，获得在一个完整交通信号周期内的最优相序及绿灯通行时间，之后放行该最优解中的第一个相位，等到该放行相位结束后，再更新系统状态，并将当前状态作为最优控制问题的初始状态，求解下一个最优相序。

1 交通信号可变相序的Petri网模型

Petri网有多种定义形式，其中应用比较广泛的是库所/变迁(place/transition)网。经典离散Petri网的形式化定义如下：

定义：一个Petri网系统是一个二元组，其中N=是一个网状结构。(1)P和T是不相交的，分别表示库所和变迁的有限集合；(2)Pre,Post∈N|P|×|T|是关联矩阵，N表示非负整数集合；(3)M0∈N|P|是系统的初始状态。

假设pi,i=1,2,…,|P|和tj,j=1,2,…,|T|分别表示库所和变迁，在Petri网模型图中通常用圆圈和矩形框表示。在关联矩阵中，如果Pre[i,j]>0，则在网系统中有一条从pi指向tj的弧，弧上的权重为Pre[i,j]；在关联矩阵Post中，如果Post[i,j]>0，则在网系统中有一条从tj指向pi的弧，弧上的权重为Post[i,j]。如果模型中的一条弧上不标明数字，则默认该条弧上的权重为1。Petri网的标识状态(又称为marking)由分布在各个库所中的托肯(token)表示。系统的全局标识状态向量用M表示，非负整数M[pi]表示库所pi中包含的托肯个数，也称为库所的标识。在系统状态M下，一个变迁被称为使能(enabled)，当且仅当该变迁的输入库所中都包含有足够多的托肯，并使得式1成立。

∀pi∈*tj,M[pi]≥Pre[i,j]

(1)

其中，*tj表示变迁tj的所有输入库所的集合。

当一个变迁使能时，该变迁具备触发(fire)条件，即系统中有足够的资源在其输入库所中。一个变迁触发后会将其输入库所中的资源(托肯)转移到其输出库所中。当一个或者多个变迁触发后，系统进入新的状态M'，并满足基本状态等式2。

M'=M0+(Post-Pre)·σ,M'∈N|P|,σ∈N|T|

(2)

其中，σ为触发向量，σ[j]为系统从初始状态M0进入状态M'的过程中，变迁tj触发的次数。

道路交通系统模型可以大致划分为车流模型、交叉口模型，以及信号灯及其控制模型等部分。文中重点考虑交叉口及信号灯控制模型，对于非交叉口内的部分，只考虑进出交叉口的禁止车辆随意变道区域的车流模型。如图1(a)所示的交叉口模型，4个方向均为双向六车道，且每个方向进入交叉口车流分为直行、左转和右转。

(a)交叉口车流示意图 (b)4相位信号控制方案

(c)交叉口车流的Petri网概括模型

根据车流模型的定义并假设交通信号系统采用固定相序，文中使用比较通用的4相位信号控制方案，如图1(b)所示。相位1和2分别为允许南北方向的直行加右转和左转车流通行；相位3和4分别为允许东西方向的直行加右转和左转方向车流通行。

图1(c)为该交叉口的Petri网概括模型(利用库所和变迁的局部特性(locality)，可通过逐步细化得到满足仿真要求的加细模型[13])。模型中的库所用于对交叉口内的或者准备进入交叉的车流建模，而变迁用于对车流驶入或者驶出对应车流队列的事件建模。为了便于说明，对模型中的所有节点采用了统一的命名方式。对于变迁，其命名规则为tx(y)z，其中x=n,s,w,e分别表示北、南、西、东四个方向，y=l,c,r分别表示左转、直行和右转，z=i,o分别表示驶入和驶出。例如，变迁twli的含义为从交叉口的西面驶入左转车道，变迁two的含义为从交叉口的西面驶出交叉口。对于库所，采用了类似的命名规则px(y)(z)，例如库所pwc表示从交叉口西面进入直行车道的车流队列，库所peo表示从交叉口东面驶出的车流队列。库所在状态M下的托肯数M[px(y)(z)]代表了对应车流队列中车辆的个数。以从交叉口西面进入左转车道，并由从交叉口北面驶出交叉口为例。车辆到达左转车道时变迁twli被触发，相应车流队列的排队数加1，即M[pwl]加1；随后变迁twlo被触发，车辆驶出左转车道，进入交口北面驶出车流队列(由库所pno表示)；最终变迁tno被触发，车辆驶出交叉口。

根据交通信号控制系统的特性，采用基于有限语义服务器语义(finite server semantics)的固定时延(constant delay)离散时间Petri网进行建模。对于车流部分，采用基于无限服务器语义(infinite server semantics)的随机时间Petri网建模，也就是说，每个变迁的触发延迟时间为符合指数分布的随机数[10]。基于无限服务器语义的离散时间Petri网，又称为马尔可夫Petri网(Markovian Petri net)。对于在一个指定标识M下的变迁tj，其触发时间符合参数为λj·enab(tj)的指数分布，其中λj为变迁的触发速率，enab(λj)为变迁的使能度。

(3)

马尔可夫Petri网及其在交叉建模中的应用具体可参见文献[8]。基于无线服务器语义的连续时间Petri网得到了广泛的应用[14-16]。在任意时间点τ，变迁tj的输出流(flow)被f(tj,τ)定义为:

f(tj,τ)=λj·enab(tj,τ)=

(4)

可以看出，在连续Petri网中，变迁的使能度不再限制为整数。

道路交叉口模型中的另一个重要部分是信号控制模型。为方便讨论，文中将绿灯和黄灯归为一类允许通行信号，因此信号周期由各个相序的通行时间之和组成。传统的固定相序信号控制方法中，各个相位的车流根据预先设定好的固定顺序依次获得通行权。该方法虽然简单，但是却没有充分考虑各个方向到达车流量的动态特征，无法对车流的变化做出及时有效的响应，优化空间较小。因此，文中提出了一种基于Petri网的可变相序控制模型，系统根据优化目标函数，动态选择相序及每个相位的绿灯通行时间。图1(b)中4相位交通信号系统的可变相序控制模型如图2所示。

模型中库所p1,p2,p3,p4用于对相位1到相位4的通行绿灯状态建模，当库所中含有托肯时，表示其对应相位中的车流具有通行权。例如，如果库所p1中含有托肯，则相位1中的车流2、3、8、9具备了通行权(见图1)。库所pe1,pe2,pe3,pe4用于确保在一个完整的信号周期内，任何一个相位都只能获得一次通行权，从而避免某个相位的车流长时间处于等待状态；在状态M下，如果M[pei]=1，表示在当前的信号周期内，相位i尚未获得过绿灯通行权，其中i=1,2,3,4；只有当库所p0和pei同时含有托肯时(M[pei]=M[p0]=1)，相位i才有机会获得绿灯通行权。库所ps的作用是标识一个新的信号周期的开始。在文中的4相位交通信号控制模型中，M[ps]=4表示所有的相位都获得了一次通行权，信号控制系统将进入下一个信号周期。

图2 交叉口4相位可变相序交通信号控制模型

变迁t1、t2、t3、t4为瞬时变迁(immediate transition)，也就是假设其变迁触发时间为零。当瞬时变迁被使能时，立即完成触发并更新系统状态。变迁ta、tb、tc、td为固定时延变迁(determined delay transition)，每个变迁具有一个延迟时间，分别表示为δa、δb、δc、δd。当一个固定时延变迁在时间点τ被使能，则经过其对应的时延δi，在时间点τ+δi变迁ti完成触发并更新系统状态。

在初始状态下，M[pe1]=M[pe2]=M[pe3]=M[pe4]=M[p0]=1，因此变迁t1、t2、t3、t4都被使能，这在Petri网模型中形成了一个典型的冲突关系；在对应的交通信号模型中，这意味着所有的相位都有机会在下一时刻获得绿灯通行权。因此，Petri网模型中的冲突解决策略决定了信号系统的相序选择。例如，假设此时的冲突解决策略是变迁t1、t2、t3、t4的优先级依次降低。在初始状态，变迁t1将优先获得触发，库所p0和pe1中的托肯被转移到p1中，因此相位1对应的车流获得绿灯通行权，此时ta被使能；经过时延δa(相位1的绿灯通行时间)后，变迁ta触发，库所p1中的托肯重新转移到p0中，同时库所ps也获得一个托肯；注意，此时库所pe1中的托肯被清空，因此变迁t1不再使能，即在该周期内相位1不再获得通行权；根据优先级，下一时刻变迁t2触发(相位2的车流获得通行权)；当变迁t1、t2、t3、t4全部获得触发后，库所pe1,pe2,pe3,pe4中的托肯全部被清空，而ps获得4个托肯，因此变迁ts被使能，ts触发后系统信号控制系统回到初始状态，意味着一个新的信号周期开始。

2 基于MPC的可变相序优化算法

预测模型的建立和滚动优化过程是MPC控制算法的核心。文中创新性地将MPC算法框架应用到交通信号可变相序的优化问题中。

在任一个信号周期的起始时刻，以信号周期的总时长作为MPC模型的优化时间域，通过建立优化函数，求解在该信号周期内的最优相序策略；在获得当前时间点的相序及绿灯通行时间后，应用当前第一个相位的通行策略，直到该相位绿灯时长结束；之后在下一相位通行开始前，再滚动式地优化有限时域内的控制策略，获取下一个最优相位及其绿灯通行时间。需要注意的一点是，虽然与传统MPC算法类似，为了使得模型能够尽量细致地描述系统在整个时间域内的动态特征，从而取得较好的优化效果，在优化模型中采用了较小的步长(1s)。但是由于每个相位的通行时间必须是连续的，因此在计算出当前采样时刻的最优控制策略后，采取的控制动作不以优化步长为单位，而以单个相位的通行绿灯时长为单位。

根据图1、图2中的交通流及信号控制模型，求解最优相序的问题可以转换为求解变迁t1、t2、t3、t4的最优冲突解决策略问题。定义对角线矩阵W为冲突解决矩阵，其对角线元素的定义如下：

(5)

其中，Λ={t1,t2,t3,t4}。

相序优化考虑的优化指标可以有很多种，比较常用的包括排队长度、车流通过率、车流停留时间等。在该算法中，假设当前的采样时刻为τ，在一个完整信号周期T中，交叉口内各方向车流平均排队长度构造相序优化的目标函数J为：

(6)

其中，pi∈ψ={pno,pwo,peo,pso}；Mτ+δ[pi]表示在时刻τ+δ库所pi对应队列的排队长度。

本文标题，取意于宋代无名氏的《一剪梅·漠漠春阴酒半酣》最后一句：“篝灯强把锦书看。人在江南，心在江南”。此时的作者，在“江南”耶、不在耶？——所谓“锦书”指夫妻间书信，传情递意，且要“篝灯强看”，那般地眷恋、向往、思念，是全词情意落位的重心点。

在每一个采样周期，通过解决优化问题(见式7)，求解在信号周期内的T个最优的冲突解决矩阵Wτ,Wτ+1,…,Wτ+T：

(7)

3 算法仿真及比较结果

针对图1中的4相位道路交通交叉口信号控制系统，本节基于混合结构的Petri模型(交通流使用了连续时间Petri网，其他采用离散时间Petri网)，分别使用固定相序模型以及图2所示的可变相序模型进行定量的仿真及比较分析。

对于车流模型，假设变迁ti对应的车流到达和离开时间的间隔都符合参数为θi=1/λi的指数分布，在连续模型中采用无限服务语义模型，则变迁的触发速率为λi。假设在交叉口外，每个车流方向不允许变道区域的最大排队长度限制为20；驶出交叉口的车流最大排队长度限制为30(通过在模型中加入自环库所实现，可参考文献[12,16])。

文中定量地比较了交叉口内各个车流队列的平均排队长度L，也就是模型中库所pno,pwo,pso,peo的平均托肯数量。实验中采用基于Matlab的Petri网仿真工具，经过100次仿真后取平均值。L定义如下：

(8)

其中，K=100为仿真次数;ψ={pno,pwo,peo,pso}。

表1 车流Petri网模型参数配置

采用传统的固定相序信号控制策略，以及文中提出的可变相序模型和优化算法(两种方案采用的总信号周期相同)，分别在Matlab下进行仿真，得到的仿真结果如表2所示。

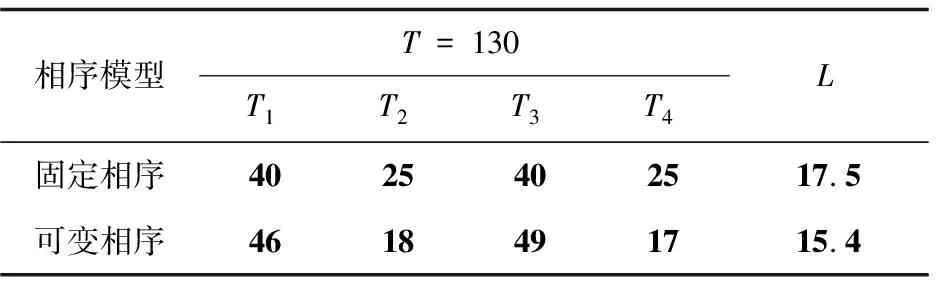
表2 仿真结果比较

从仿真结果中可以看出，使用可变相序模型以及基于MPC的相序优化算法，交叉口的平均排队长度优化了12%(从17.5降到15.4)。

4 结束语

道路交叉口交通信号的优化能够进一步提高车辆的通行效率以及道路资源的利用率，因此一直是交通系统控制与优化的热点问题，在智能交通迅速发展的今天尤其受到重视。针对传统固定相序交通信号控制机制的不足，提出了基于Petri网的可变相序控制模型，并结合MPC算法框架实现了相序与通行时间的优化。仿真结果表明，与传统固定相序算法相比，该算法能有效减少交叉口内各方向的平均排队长度，从而减少了拥堵。