基于关键点的不确定时间序列线性降维方法
汤其婕,朱小萍
(南京航空航天大学 计算机科学与技术学院,江苏 南京 211106)
0 引 言
时间序列(time series)是一种典型的高维数据类型,也是数据挖掘[1-2]领域中主要研究的对象。一条时间序列是一组序列数据,它通常是在相等间隔的时间段内,依照给定的采样率,对某种潜在过程进行观测的结果。它广泛存在于工业、农业及商业等领域,与人们的生活息息相关。其典型数据包括航天飞船等重要仪器每一时刻的运行状态数据、医疗设备记录的病人每时每刻的心率变化等。研究如何有效地从这些复杂的海量时间序列中挖掘潜在的有用信息,具有重要的理论价值与现实意义[3-4]。
在实际生产生活中,时间序列的产生通常受不确定因素的影响,如数据采集设备的缺陷和环境影响,导致数据采集与实际数据有一定的偏差;或者出于隐私安全考虑,人为地将一定程度的偏差引入到数据中。这些偏差导致时间序列在每一个点上的取值对应一个可能值的集合,无法给出其确定值。将这类型的数据定义为不确定时间序列。加之时间序列本身具有的海量、高维等特征,若直接对原始不确定数据进行数据挖掘等操作,效率很低。而解决这一问题最直接的方法就是对原始数据进行预处理操作。但是由于不确定时间序列与确定时间序列在取值上的不同之处,原有用于确定时间序列上的方法则不适用于不确定时间序列。因此,结合已有的针对确定数据的处理方法,找到适用于不确定时序数据的预处理方法,是目前针对不确定时间序列研究的重点,也是文中主要研究的问题。
文中主要研究了基于关键点的线性降维算法与统计模型相结合的不确定时间序列线性降维问题。首先对不确定时间序列进行有效的描述统计建模,将不确定时间序列归约为三条确定的时间序列,进行空间维度的一次降维;然后分别对三条确定时间序列进行关键点的选取,进行时间维度的二次降维;最后,综合空间维度和时间维度的两次降维,得到整个不确定时序数据集的关键点,完成整个降维工作。
1 相关工作
1.1 线性表示的提出
针对确定时间序列的预处理,已有许多成熟的方法,如傅里叶变换[5](DFT)、离散小波变换[6](DWT)、奇异值分解[7](SVD)等等。以上几种方法在某些方面具有明显的优势,但是也存在不足。例如,傅里叶变换、离散小波变换存在一个共同缺点,即过度除噪。消除了局部极值点,造成重要信息遗失,数据表示误差较大;奇异值分解法依赖数据,该方法由于使用数据集产生新的基向量,数据项的任何改变都需要重新计算,时间复杂度大。基于以上几种算法的不足,时间序列线性表示[8-9]方法被提出,其主要目的是有效地保留数据的主要特征,对数据进行高效的降维处理。
1.2 传统时间序列的线性表示
传统的时间序列线性表示方法的主要思想就是用一系列前后相互连接的线段近似表示原始数据,其关键之处在于分段点的选用[10]。线性表示在时间序列的应用上有如下几个优点:理论简单,实现容易;压缩率可以调整。既保留数据的特点,又进行有效的降维。近年来,国内外许多学者对线性表示方法进行了深入研究,提出了许多优秀的线性表示方法。文献[11-12]各自独立提出了分段聚合近似(PAA)的时间序列线性表示方法,该方法的主要思想是首先将时间序列按照相同的时间跨度进行划分,然后以每个时间序列子段的平均值来近似表示相应子段。文献[8]介绍了一种基于重要点的线性表示方法(PLR-IP),即如果一个点在局部区间内与区间端点的比值超过设定的阈值R,则认为它是重要点。通过调节阈值R,可以获得不同精度的线性表示。文献[9]介绍了基于特征点的线性表示方法(PLR-FP),该方法的思想是首先提取时间序列的极值点,然后根据每个极值点保持的时间跨度去除噪声点。文献[13]介绍了一种基于斜率提取边缘点的时间序列线性表示方法(PLR-SEEP),该方法的主要思想是首先设定阈值,然后根据斜率变化选取分段点。
2 不确定时间序列描述统计模型建模
不确定时间序列与传统时间序列相比,主要的不同之处在于每个时间点的取值。前者是一个取值的集合,且每一个数值对应该数值在该时间戳发生的概率,后者是一个确定的数值。因此,针对传统时间数据对数值的处理,需要转换为对集合的处理。
定义1(集中趋势):在描述统计学中,观察值在分布中心位置的聚集现象称为分布的集中趋势,一个分布中心特征的统计度量称为集中趋势的度量。数据集中,平均值是最常用、最具代表性的度量。其中,算数平均值,是整体数学期望的无偏估计。大数定律规定,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值(expected value)。因此,文中选择观察值集合的期望值作为观察值的集中趋势度量,记为vt,ey,表示不确定时序数据的集中趋势。例如,给定某一时间点的观察值及对应的概率{(5,0.3),(6,0.4),(7,0.2),(8,0.1)},则该点的集中趋势为5×0.3+6×0.4+7×0.2+8×0.1=6.1。
定义2(MME-Line不确定时间序列):长度为n的MM-Line不确定时间序列由一条包含n个元素的序列构成,记为:
TSUMME-Line={([v1,min,v1,max],v1,ev),([v1,min,v1,max],v1,ev),…,([vn,min,vn,max],vn,ev)}
(1)
其中,每个元素是一个二元组,由该时刻的观察值区间及其集中趋势组成;ti表示第i个时刻,序列中所有时刻的最大观察值所构成的序列叫作最大值序列,其相连之后所得曲线叫作最大值曲线,记为Max-Line。同样,所有最小观察值构成最小值序列,相连后曲线记为Min-Line;所有集中趋势构成集中趋势序列,记为EV-Line。例如,不确定时间序列TSUMME-Line={([2.5,4.2],3.3),([3.6,7.9],5.5),([4.5,9.2],7.6),([3.8,7.2],6.2),([6.0,10.8],8.3),([5.1,9.6],9.6)},所有最大观察值(3.3,7.9,9.2,7.2,10.8,9.6)构成Max-Line序列,所有最小值(2.5,3.6,4.5,3.8,6.0,5.1)构成Min-Line序列,所有集中趋势(3.3,5.5,7.6,6.2,8.3,9.6)构成EV-Line序列。
定义3(MME-Line描述统计模型):不确定时间序列描述统计模型包括三条等长的确定时间序列:Max-Line、Min-Line和EV-Line。因此,不确定时间序列MME-Line的向量形式表示如下:
(2)
其中,XMax-Line为Max-Line序列;XMin-Line为Min-Line序列;XEV-Line为集中趋势序列。
由此,对不确定时间序列的降维可以归约为对这三条确定时间序列的降维。
3 基于关键点的不确定时间序列线性降维
3.1 选取关键点
关键点是反映时间序列数据特征的重要点,也是对时序数据进行分段的点,体现了时间序列的轮廓和集中趋势。如图1所示,图中1、2处的关键点是典型的极值点,其可以通过极值法求出;但3~5处的转折点并不能通过极值法求出,而文献[8]证明,该类型的点在时间序列数据集中也是包含大量重要信息的数据点。文中关键点的选择包括极值点和转折点两部分。
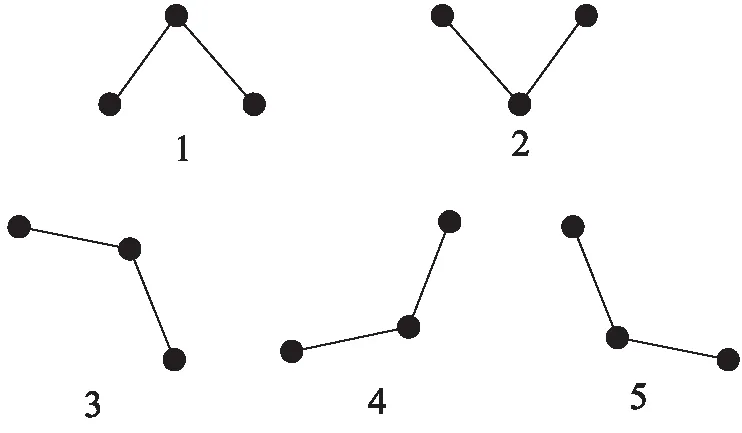
图1 关键点举例
定义4(转折点):在不超过序列的最大值和最小值下,由三点组成的简单时间序列,夹角越小,角处的顶点成为转折点的可能性就越大。将该点称为转折点。
定义5(阈值参数):由三点组成的时间序列,A、O、B,其端点O是否为转折点,决定于三点数值是否满足条件|Data(A)+Data(B)-2*Data(O)|≥C。其中C即是自定义的阈值参数,其大小决定于所选数据的类型,Data(*)表示在时间点*处的数值。
数据的压缩程度可以通过调节阈值参数来设置。阈值参数设置越大,则数据压缩程度越大;反之,数据压缩程度越小,数据分段越精细。
3.2 选取关键点算法
由3.1可知,关键点的选择包含极值点和转折点两部分。通过对描述统计模型中的三条确定时间序列分别进行关键点的选取,可以得到三个关键点的集合,分别是Max-Line关键点集合、Min-Line关键点集合和EV-Line关键点集合。算法的具体过程如下。
算法:MME-KP
输入:不确定时间序列TSU={(t1,V1,P1),(t2,V2,P2),…,(tn,Vn,Pn)},阈值参数C1、C2、C3,时阈参数T
输出:三条确定时间序列关键点集合
1 double []MaxNum; double []MinNum; double []EVNum;
2 for(i=0;i<1;i++){
3 sort(Vi);
4 vi,ey=pi,1*vi,1+pi,2*vi,2+…+pi,n*vi,n;
5 MaxNum[i]=vi,max; MinNum[i]=vi,min; EVNum[i]=vi,ey;}
6 ArrayList MaxKP; ArrayList MinKP; ArrayList EVKP;
7 for(i=0;i8 if(MaxNum[i]是极值点){
9 MaxKP.add(i);
10 }else if(MaxKP[i]是转折点 && !MaxKP.contains(i){
11 MaxKP.add(i);
12 }
13 }//MinKP和MaxPV的计算与MaxPV类似
14 MaxKP=getKPArrayList(MaxKP, T); //对关键点进行进一步筛选,使其满足时间跨度T
15 MinKP=getKPArrayList(MinKP, T);
16 EVKP=getKPArrayList(EVKP, T);
3.3 算法分析
MME-KP算法首先通过提出的描述统计模型将不确定时间序列归约为3条确定时间序列,即最大值序列、最小值序列和集中趋势序列,有效提取了数据的三个主要特征。其次,对三条归约得到的确定时间序列分别进行两遍扫描选取关键点。其中关键点包含了极值点和转折点两部分,基本保留了数据的全部特征。同时,该时间序列线性降维算法综合考虑了时间跨度的选择,可以根据不同数据的特点动态设置阈值参数C和时阈参数T,改变数据选取的精细程度和数据的压缩度。综上,该算法既能较好地保留时序数据的特征关键点,同时又能有效降维。算法的复杂度为O(n),n为时间序列的长度[14]。
4 实 验
4.1 实验目的和实验环境
为了验证文中提出的基于关键点的线性降维算法与描述统计模型相结合的实际效果,选取了10个不同领域的时间序列数据集进行实验。实验以压缩率和拟合误差作为评价优劣的指标,将MME-KP算法与PAA算法以及PLR-FP算法进行对比。
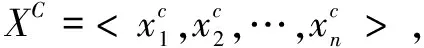
(3)
拟合误差是用来衡量拟合时间序列与原始时间序列差异性的一个重要指标。在同等压缩率的情况下,拟合误差越小,表示拟合效果越好,拟合数据越接近真实数据。
4.2 实验数据处理
确定时间序列是一组按时间先后顺序排列的精确数据,这些数据通过加入扰动成为不确定化数据,由此成为不确定时间序列。给定某一时刻i,不确定时间序列在该时刻的值可表示为:
Vi=di+ei
(4)
其中,di为确定时间序列i时刻的精确值;ei为该时刻误差,通常服从某种概率分布。
文中实验数据取自于www.cs.ucr.edu/~eamonn/tutorials.html公布的用于数据挖掘的通用实验数据集(KP-Data),如表1所示。将每个数据集的训练子集和测试子集重新配置整合,获得实验数据集。同时,通过不确定化模型将不确定性引入到确定序列中,人为加入扰动形成误差ei,并使ei服从某种分布,从而将序列转化成不确定时间序列。
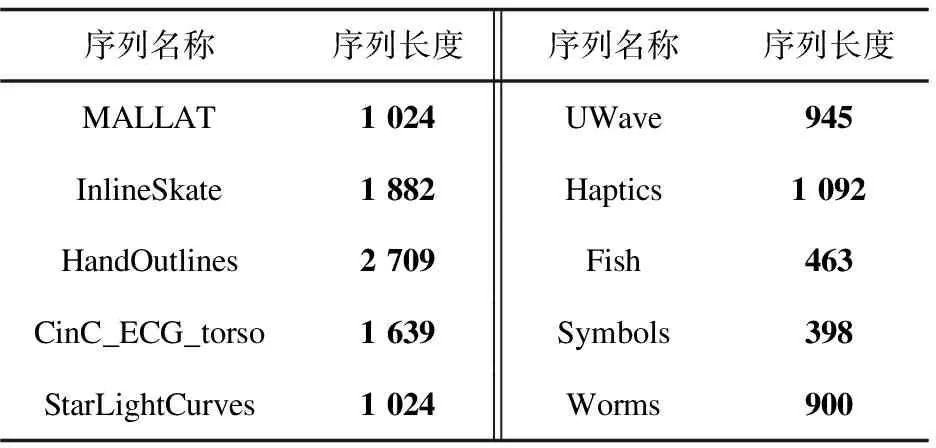
表1 KP-Data数据集
4.3 实验方法
实验主要分为两部分:
(1)将原始数据进行统计模型建模,每种类型的数据将分别建模得到三条确定时间序列数据:最大值序列、最小值序列和集中趋势序列;
(2)在步骤1建立的模型基础上,分别用提出的MME-KP算法、Yi和Keogh提出的分段聚集近似(PAA)线性表示方法,以及文献[9]提出的PLR-FP线性表示方法对数据分别进行处理,得到整个不确定时序数据集的关键点集合。最终以同种压缩率的标准下拟合误差的大小作为评估算法质量的指标。拟合误差越小,算法性能越好。
4.4 实验结果与分析
(1)第一部分。
在提出的统计模型下,部分数据的建模表示如图2所示。
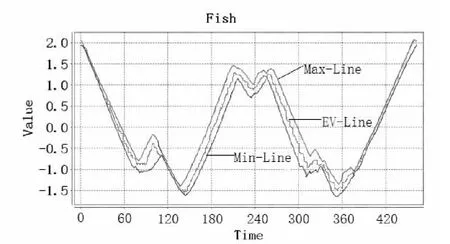
(a)Fish原始数据图
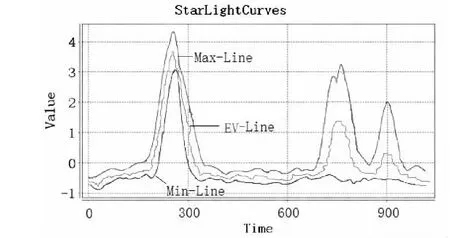
(b)StarLightCurves原始数据图
(2)第二部分。
文中提出的MME-KP需要输入3个阈值参数:C1、C2和C3,分别对应三条确定时间序列,即最大值时间序列、最小值时间序列及集中趋势时间序列的关键点阈值参数。参数设置越大,数据的压缩率越小,拟合误差越大;参数设置越小,数据压缩率越大,数据分段越精细,拟合误差越小。实验选取的数据来自10个不同领域,数据的差异性较大。为了对比实验的公平性,将根据不同数据类型调整参数,保证在10组数据的压缩率都在50%的基准下,进行三种算法的拟合误差对比。在同一压缩率情况下,拟合误差越小,算法性能越好。
部分实验结果如图3所示。
从图3中可以看出,在10个通用时间序列数据集中,MME-KP算法在其中7个数据集上Max-Line拟合序列的误差最小,在另外三个数据集中,误差与最好的算法相当。同时,由图(b)可以看出,在EV-Line上的拟合误差,MME-KP算法明显优于其他两种算法,在10个数据集中都保持优势。实验结果说明,采用了极值点与转折点相结合的选取关键点算法,在数据降维上具有明显优势。因为其在保留了极值点这一数据的明显特征外,还适当选取了体现数据特征的转折点,减小了一些重要点被粗暴舍弃的概率,提高了数据选取的精细度,从而降低了拟合误差。
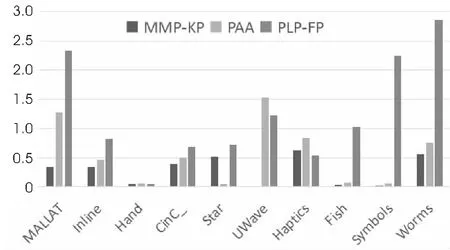
(a)三种算法在Max-Line上拟合误差的比较
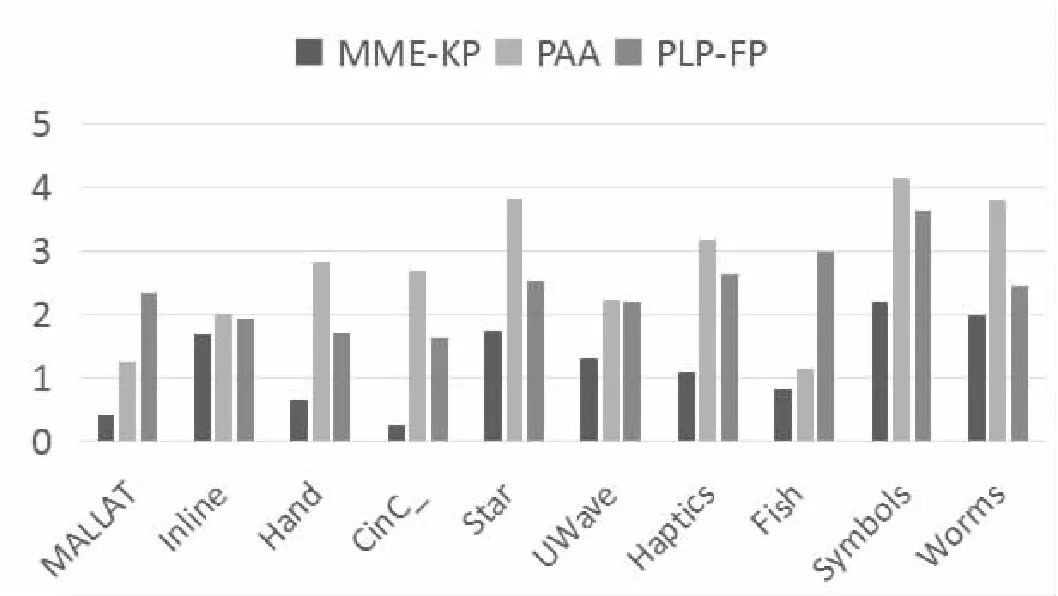
(b)三种算法在ME-Line上拟合误差的比较
同时实验结果显示:对于短时间内波动频率比较平缓的时间序列,MME-KP算法的实验效果与其他两种算法相比,优势并不是很大,如图4中的对比1所示,MME-KP算法和PAA算法都能较好地拟合MALLAT的原始数据。但是对于短时间内波动频率剧烈的时间序列,如图4中的对比2所示,数据在短时间内波动较大,MME-KP算法的拟合效果就远胜于PAA算法。主要原因是,在短时间内,时间序列波动较大,会产生大量极值点,对于以找极值点和转折点为主要关键点的MME-KP算法来说会捕获大量关键点,从而保证了数据主要特征的不流失。而对于PAA算法,它主要思想是以一段时间内的数据均值来代替这段序列,所以,在短时间内时间序列波动较大的情况下,在这段时间内的数据均值波动并不会很大,相对地,它的拟合序列与原序列相比,就会丢失很多重要点信息,造成拟合误差较大。
综上,MME-KP降维方法在与提出的描述统计模型的结合上,有以下几点优势:在降维效果上,可以通过参数的改变,进行不同压缩率的降维。参数设置越高,数据压缩程度越大。在现实应用中可以根据实际需求选择所需的降维效果;在与其他线性降维方法PAA以及PLR-FP的比较过程中,MME-KP方法体现出了更为良好的拟合效果,误差更小,与原始数据保持高度的一致性。
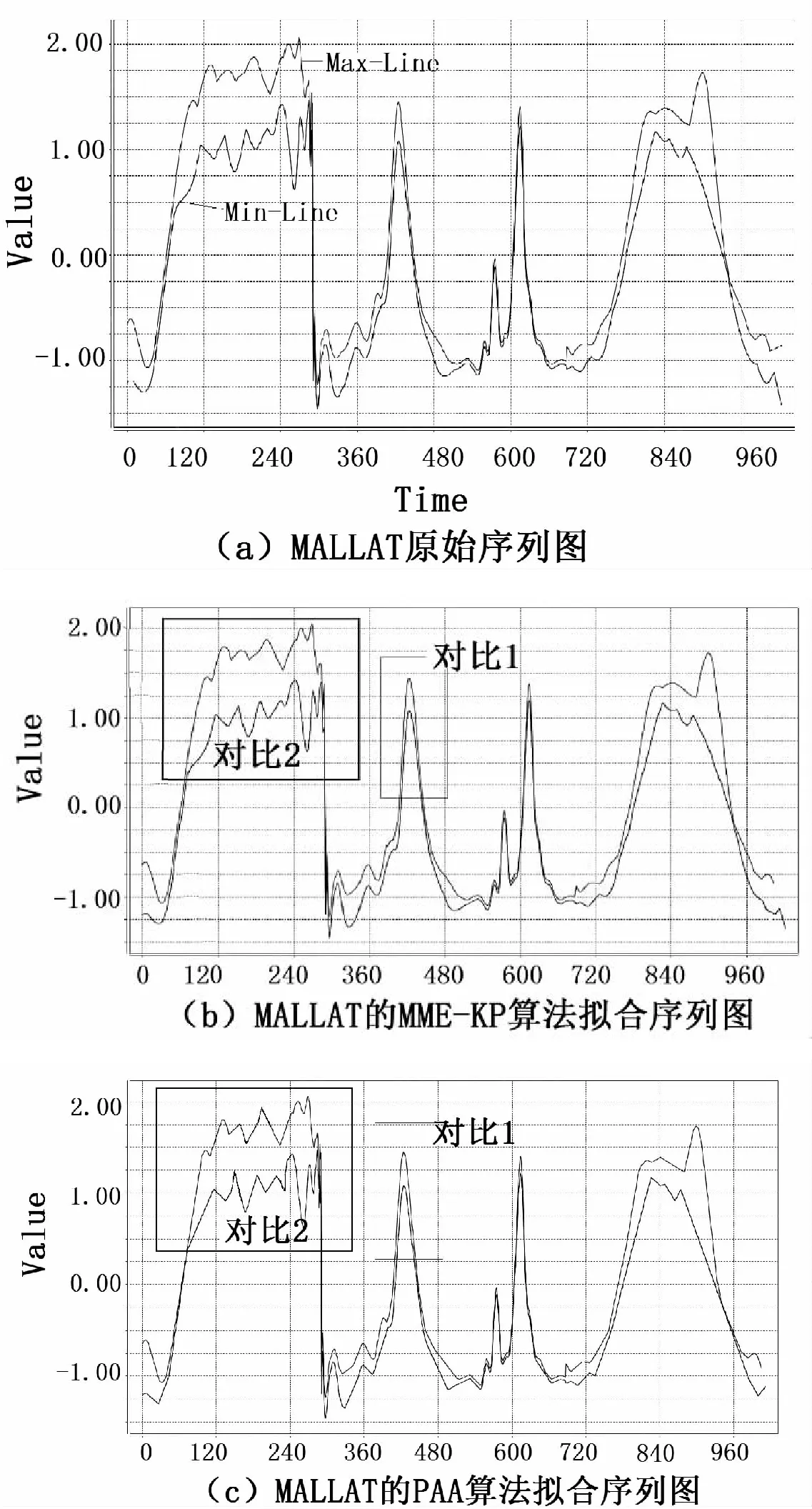
图4 实验对比
5 结束语
针对不确定时序数据区别于确定时序数据的主要特征,首先提出不确定时间序列向确定时间序列归约的描述统计模型,同时综合考虑已有的确定时间序列的线性分段思想,提出综合考虑极值点与转折点的关键点选取算法。综合以上两点,将不确定时序数据进行空间和时间上的有效降维。实验结果表明,该算法在数据降维效果上有良好的性能,且能高度还原原始数据。下一步的研究工作是在所提出模型的基础上找到更合适的原始数据拟合方案。
猜你喜欢
混动成为降维打击的实力 东风风神皓极车主之友(2022年4期)2022-08-27 论建筑工程管理关键点建材发展导向(2022年3期)2022-04-19 基于数据降维与聚类的车联网数据分析应用汽车实用技术(2022年4期)2022-03-07 极值(最值)中的分类讨论新世纪智能(数学备考)(2021年10期)2021-12-21 极值点带你去“漂移”新世纪智能(数学备考)(2021年10期)2021-12-21 肉兔育肥抓好七个关键点今日农业(2021年8期)2021-11-28 建筑设计中的防火技术关键点建材发展导向(2021年11期)2021-07-28 极值(最值)中的分类讨论新世纪智能(数学备考)(2020年10期)2021-01-04 极值点偏移问题的解法语数外学习·高中版中旬(2020年10期)2020-09-10 Helicobacter pylori-induced inflammation masks the underlying presence of low-grade dysplasia on gastric lesions
8 if(MaxNum[i]是极值点){
9 MaxKP.add(i);
10 }else if(MaxKP[i]是转折点 && !MaxKP.contains(i){
11 MaxKP.add(i);
12 }
13 }//MinKP和MaxPV的计算与MaxPV类似
14 MaxKP=getKPArrayList(MaxKP, T); //对关键点进行进一步筛选,使其满足时间跨度T
15 MinKP=getKPArrayList(MinKP, T);
16 EVKP=getKPArrayList(EVKP, T);
3.3 算法分析
MME-KP算法首先通过提出的描述统计模型将不确定时间序列归约为3条确定时间序列,即最大值序列、最小值序列和集中趋势序列,有效提取了数据的三个主要特征。其次,对三条归约得到的确定时间序列分别进行两遍扫描选取关键点。其中关键点包含了极值点和转折点两部分,基本保留了数据的全部特征。同时,该时间序列线性降维算法综合考虑了时间跨度的选择,可以根据不同数据的特点动态设置阈值参数C和时阈参数T,改变数据选取的精细程度和数据的压缩度。综上,该算法既能较好地保留时序数据的特征关键点,同时又能有效降维。算法的复杂度为O(n),n为时间序列的长度[14]。
4 实 验
4.1 实验目的和实验环境
为了验证文中提出的基于关键点的线性降维算法与描述统计模型相结合的实际效果,选取了10个不同领域的时间序列数据集进行实验。实验以压缩率和拟合误差作为评价优劣的指标,将MME-KP算法与PAA算法以及PLR-FP算法进行对比。
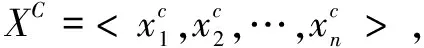
(3)
拟合误差是用来衡量拟合时间序列与原始时间序列差异性的一个重要指标。在同等压缩率的情况下,拟合误差越小,表示拟合效果越好,拟合数据越接近真实数据。
4.2 实验数据处理
确定时间序列是一组按时间先后顺序排列的精确数据,这些数据通过加入扰动成为不确定化数据,由此成为不确定时间序列。给定某一时刻i,不确定时间序列在该时刻的值可表示为:
Vi=di+ei
(4)
其中,di为确定时间序列i时刻的精确值;ei为该时刻误差,通常服从某种概率分布。
文中实验数据取自于www.cs.ucr.edu/~eamonn/tutorials.html公布的用于数据挖掘的通用实验数据集(KP-Data),如表1所示。将每个数据集的训练子集和测试子集重新配置整合,获得实验数据集。同时,通过不确定化模型将不确定性引入到确定序列中,人为加入扰动形成误差ei,并使ei服从某种分布,从而将序列转化成不确定时间序列。

表1 KP-Data数据集
4.3 实验方法
实验主要分为两部分:
(1)将原始数据进行统计模型建模,每种类型的数据将分别建模得到三条确定时间序列数据:最大值序列、最小值序列和集中趋势序列;
(2)在步骤1建立的模型基础上,分别用提出的MME-KP算法、Yi和Keogh提出的分段聚集近似(PAA)线性表示方法,以及文献[9]提出的PLR-FP线性表示方法对数据分别进行处理,得到整个不确定时序数据集的关键点集合。最终以同种压缩率的标准下拟合误差的大小作为评估算法质量的指标。拟合误差越小,算法性能越好。
4.4 实验结果与分析
(1)第一部分。
在提出的统计模型下,部分数据的建模表示如图2所示。

(a)Fish原始数据图

(b)StarLightCurves原始数据图
(2)第二部分。
文中提出的MME-KP需要输入3个阈值参数:C1、C2和C3,分别对应三条确定时间序列,即最大值时间序列、最小值时间序列及集中趋势时间序列的关键点阈值参数。参数设置越大,数据的压缩率越小,拟合误差越大;参数设置越小,数据压缩率越大,数据分段越精细,拟合误差越小。实验选取的数据来自10个不同领域,数据的差异性较大。为了对比实验的公平性,将根据不同数据类型调整参数,保证在10组数据的压缩率都在50%的基准下,进行三种算法的拟合误差对比。在同一压缩率情况下,拟合误差越小,算法性能越好。
部分实验结果如图3所示。
从图3中可以看出,在10个通用时间序列数据集中,MME-KP算法在其中7个数据集上Max-Line拟合序列的误差最小,在另外三个数据集中,误差与最好的算法相当。同时,由图(b)可以看出,在EV-Line上的拟合误差,MME-KP算法明显优于其他两种算法,在10个数据集中都保持优势。实验结果说明,采用了极值点与转折点相结合的选取关键点算法,在数据降维上具有明显优势。因为其在保留了极值点这一数据的明显特征外,还适当选取了体现数据特征的转折点,减小了一些重要点被粗暴舍弃的概率,提高了数据选取的精细度,从而降低了拟合误差。

(a)三种算法在Max-Line上拟合误差的比较

(b)三种算法在ME-Line上拟合误差的比较
同时实验结果显示:对于短时间内波动频率比较平缓的时间序列,MME-KP算法的实验效果与其他两种算法相比,优势并不是很大,如图4中的对比1所示,MME-KP算法和PAA算法都能较好地拟合MALLAT的原始数据。但是对于短时间内波动频率剧烈的时间序列,如图4中的对比2所示,数据在短时间内波动较大,MME-KP算法的拟合效果就远胜于PAA算法。主要原因是,在短时间内,时间序列波动较大,会产生大量极值点,对于以找极值点和转折点为主要关键点的MME-KP算法来说会捕获大量关键点,从而保证了数据主要特征的不流失。而对于PAA算法,它主要思想是以一段时间内的数据均值来代替这段序列,所以,在短时间内时间序列波动较大的情况下,在这段时间内的数据均值波动并不会很大,相对地,它的拟合序列与原序列相比,就会丢失很多重要点信息,造成拟合误差较大。
综上,MME-KP降维方法在与提出的描述统计模型的结合上,有以下几点优势:在降维效果上,可以通过参数的改变,进行不同压缩率的降维。参数设置越高,数据压缩程度越大。在现实应用中可以根据实际需求选择所需的降维效果;在与其他线性降维方法PAA以及PLR-FP的比较过程中,MME-KP方法体现出了更为良好的拟合效果,误差更小,与原始数据保持高度的一致性。

图4 实验对比
5 结束语
针对不确定时序数据区别于确定时序数据的主要特征,首先提出不确定时间序列向确定时间序列归约的描述统计模型,同时综合考虑已有的确定时间序列的线性分段思想,提出综合考虑极值点与转折点的关键点选取算法。综合以上两点,将不确定时序数据进行空间和时间上的有效降维。实验结果表明,该算法在数据降维效果上有良好的性能,且能高度还原原始数据。下一步的研究工作是在所提出模型的基础上找到更合适的原始数据拟合方案。

