同伦方法在图像稀疏去噪中的应用
张梦磊 刘 舟 任俊英 余 磊
(武汉大学电子信息学院,湖北武汉 430079)
1 引言
基于稀疏表示的图像去噪算法是近年来的研究热点之一,其中利用稀疏表示中的字典进行图像去噪的方法尤其受到研究人员的青睐。稀疏表示中的字典从开始的正交基发展到冗余的正交基,再到现在的超完备字典,而字典的选择方法也从开始的使用单一固定的字典变化到现在利用图像自身的特点和结构进行字典学习选择自适应的字典,使得字典能更好的表现图像的结构,从而更有利于噪声的去除。目前研究人员已经提出了许多有效的字典学习方法。
常用的字典学习方法包括最优方向(MOD)算法[1],该算法字典更新方式简单,但是算法的收敛速度很慢。在该算法的基础上,一些比较著名的算法比如K-SVD 算法及其改进算法[2-5]被提出。K-SVD 算法的主要思想是:在超完备训练字典的前提下,不断地对字典中的原子进行调整和更新,达到和训练向量集最大程度的匹配,从而完成字典学习过程。与 MOD 等算法相比,K-SVD算法的时间复杂度低,并且在图像去噪方面也取得了不错的效果。文献[6]中的结果显示经过训练后的字典用于图像去噪的效果比单一固定的字典的效果好。文献[7]将非参稀疏贝叶斯方法用于字典学习,同时引入结构先验,并将其应用于图像去噪,该方法优点是不需要预先设置各种参数,但是该方法的收敛速度较慢。
同伦(连续)方法是一种启发式的算法,它的主要思想是设置一个较为简单的初始问题并求解,然后将初始问题不断转化为目标问题,利用上一个问题的求解结果求解当前问题,最终得到目标问题的解。文献[8-10] 将同伦方法用于1-范数最小化问题以及动态信号恢复问题的求解,并得到了很好的结果,充分显示了同伦方法在解决1-范数最小化问题以及动态信号恢复问题的优越性,即更快的收敛速度以及较高的信号恢复的准确度。
本文在充分研究字典学习和同伦方法的基础上,提出一种新的图像去噪算法,该算法主要分为两个部分,第一部分是字典学习算法,使用同伦方法来更新字典,本文算法主要由三步构成,分别是:稀疏编码阶段、字典更新阶段以及正则化参数的选择阶段。第二部分主要介绍图像去噪算法,图像去噪算法需要用到由字典学习算法训练出来的字典。实验结果显示本文算法具有较好的去噪效果,同时具有较快的收敛速度。
本文的贡献如下: 1.本文提出了一种新的图像去噪算法,将同伦方法引入到图像去噪问题中; 2.通过实验验证了本文算法在不同的噪声环境下具有较好的去噪效果;3.在与K-SVD算法关于收敛速度比较的实验中,实验结果充分显示了使用同伦算法学习字典在收敛速度上的优势。
本文的安排如下:第2节介绍稀疏表示中的字典学习问题以及同伦方法;第3节详细叙述本文提出的图像去噪算法;第4节展示本文算法与当前比较流行的图像去噪算法的对比结果;第5节为本文的总结。
2 基于同伦方法的字典学习算法
2.1 同伦方法介绍
同伦(连续)方法是一种启发式的算法,它的主要思想是设置一个较为简单的初始问题并求解,然后将初始问题不断转化为目标问题,利用上一个问题的求解结果求解当前问题,最终得到目标问题的解。
(1)
其中λ被称为正则化参数,它控制着稀疏度和误差之间的平衡。
文献[8]中使用同伦算法解决(1)的思路是:若目标函数的正则化参数为λd,则首先给λ设置一个较大的初始值为λ0,并且引入参数δ,δ被称为步长,则初始问题变为:
(2)
获得式(2)的最优解后,在每次迭代中更新步长δ,通过λ(n+1)←λ(n)-δ(n)不断减小λ的值,并且求解当λ=λ(n+1)时,相应的稀疏表示系数x(n+1)。当λ的大小等于目标函数的正则化参数值λd时,此时求出x=xd即为1-范数最小化问题的最优解。图1形象描述了上述求解思路。
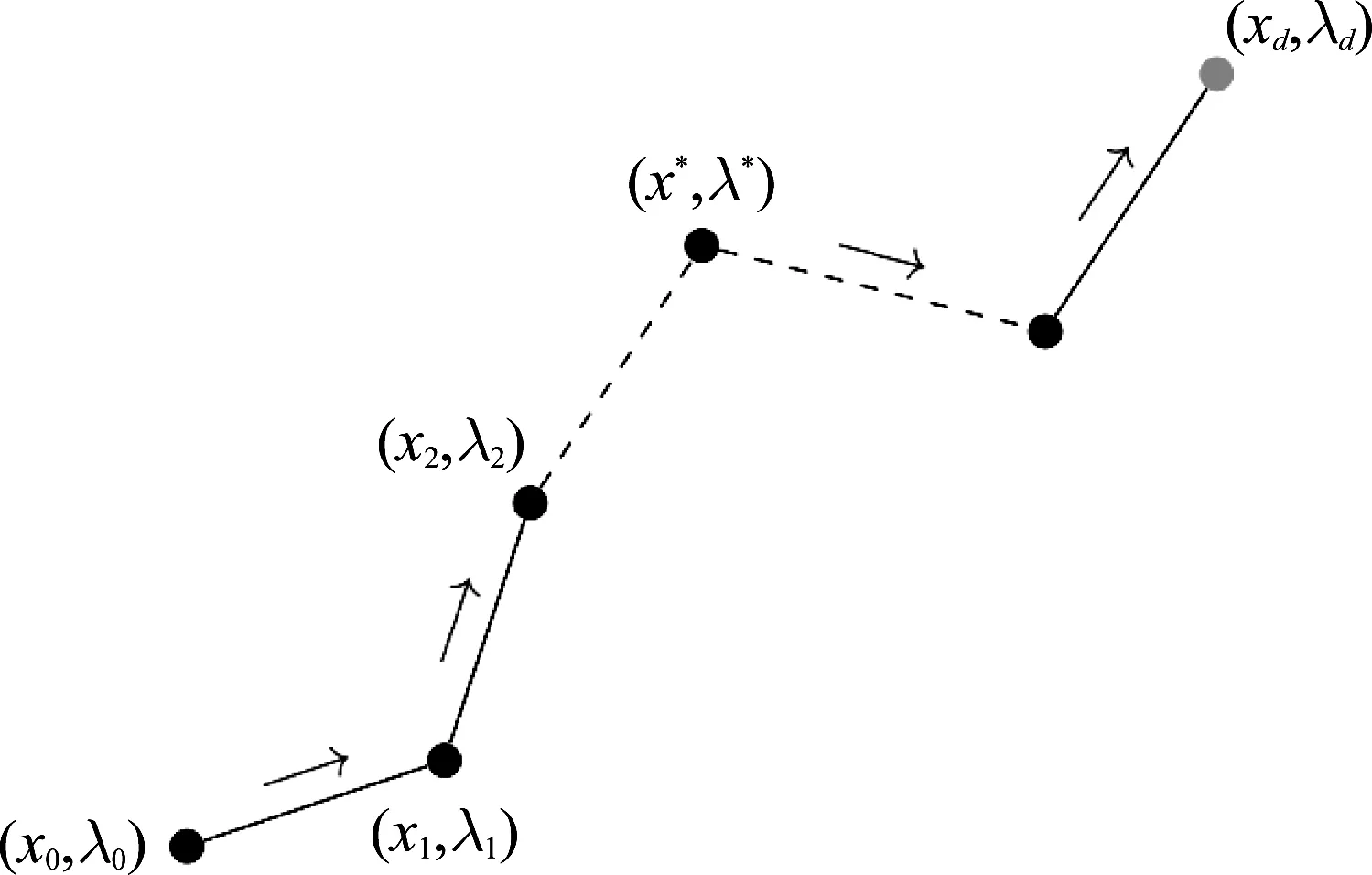
图1 同伦方法求解问题的思路
2.2 字典学习问题
字典学习问题是稀疏表示理论的一个主要内容。字典的设计包括初始化字典的选择以及字典中原子的更新,初始化字典是否合适,以及字典更新算法性能的优劣,决定字典性能的高低。
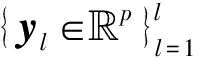
(3)
(4)
2.3 使用同伦方法进行字典学习
受同伦方法的启发,文献[11] 提出了一种自适应选择正则化参数进行字典学习的方法。该方法解决(3)的思路是:首先将正则化参数λ设置为一个较大的值,然后在每次迭代过程中不断自适应减小λ,同时更新对应的稀疏表示系数和字典,直到λ的值等于目标函数的正则化参数值λd。因此在第nth迭代中,优化问题(3)转化为:
(5)
在算法的具体实现中,主要分为稀疏编码阶段、字典更新阶段以及正则化参数λ(n)的更新阶段。对于第nth迭代中得到的(5)中的解X(n)和D(n),也会被用于第(n+1)th迭代,文献[12]表明这种方法可以有效提高字典学习算法的速度。
3 本文提出的图像去噪算法

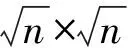
(6)
(7)
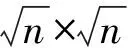
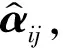
3.1 稀疏编码阶段
在字典学习算法的迭代过程进行到第nth次时,稀疏编码阶段的第kth迭代要解决如下问题:
(8)
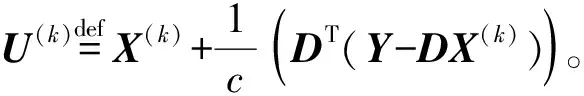
0∈2c(X-U(k))-λ(n)
(9)
(10)
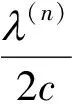
2c(X(k)-U(k))-λ(n)P(k)=0
(11)
由式(11)可以得到稀疏表示系数X(k)的表达式。
3.2 字典更新阶段
在字典更新阶段,首先固定在稀疏编码阶段获得的稀疏表示系数X,通过梯度下降法来更新字典。
在字典学习算法的迭代过程进行到第nth次时,字典更新阶段的第kth迭代的方法为:
D(k+1)=D(k)+ρ(Y-D(k)X(n))X(n)T
(12)
其中ρ为一个常数。
考虑到对字典的约束条件(4),算法需要将范数大于1的原子进行归一化。
3.3 正则化参数更新阶段
由于字典更新算法分成了稀疏编码和字典更新阶段,其中的难点在于如何保证每一次迭代过程中所获得的结果是最优的,即在两个阶段的转换过程中,怎样保证优化条件式(11)的成立。因此在正则化参数更新阶段,通过选择合适的正则化参数来保证该条件成立。
令R(n)=2c(X(n)-U(n)), 通过求解下式:
(13)
获得使优化条件(11)成立的正则化参数:
(14)
根据同伦方法的思想,需要在每一次迭代中逐渐减小正则化参数,因此令λ(n+1)=(1-ε)λopt, 其中ε为一个很小的常数。随着正则化参数的不断减小,当其等于目标函数的正则化参数值λd时,字典学习算法结束。
3.4 图像重构阶段
(15)
使用正交匹配追踪算法(OMP)[14]可以求解上式。
(16)
上式是简单的二次项问题,求解后可以得到恢复图像的闭式解:
(17)
3.5 本文提出的算法总结

表1 本文提出的算法

续表1
4 实验与分析
4.1 实验设置
本实验主要使用了Cameraman、House、Peppers、Boat、Man、Monarch、Parrot、Couple等8张经典的标准测试图像。本文主要研究图像中的加性高斯白噪声的去除。在实验中,首先将测试图像加上噪声方差为σ2的高斯白噪声,然后将带噪图像分为有重叠的大小为8×8图像块,若原图像大小为M×N,则可以得到总数为J=(M-8+1)×(N-8+1)的图像子块,将每个子块按列展开成一个列向量,则可以得到大小为64×J的训练向量组Y, 同时设置字典中的原子数为K=256。随后从训练向量组Y中训练学习得到所需的字典D,然后再将该字典D用于图像的稀疏表示,最后重构图像,得到去噪后的图像。所述步骤可以用示意图 2 说明。
本实验中采用峰值信噪比(PSNR)来评价去噪后图像的质量,PSNR越大,则表明去噪后得到的图像质量越好。
为了更好地评价本文的算法,实验中用到了其他三种比较经典的图像去噪算法作为对比算法:1)K-LLD (locally learned dictionaries)算法[15];2)BLS-GSM (Bayes least squares-Gaussian scale mixture)算法[16];3)K-SVD 算法[6]。其中 BLS-GSM算法属于经典的小波变换域图像去噪算法,使用小波变换基作为固定字典,求出在该固定字典下的小波系数,然后利用小波系数的统计特性来除噪声,最后对处理完的小波系数使用逆小波变换得到去噪后的图像。而K-LLD算法、K-SVD算法以及本文提出算法均是采用字典学习的思路,从噪声图像中训练学习得到自适应的字典,然后将该自适应的字典用于图像去噪。但是K-LLD相比于一般的字典学习方法略有不同,它是在SKR (Steering Kernel Regression)的基础上,融入字典学习的思想,自适应的学习所需字典,同时利用了图像的结构,但是该算法对于噪声没有很好的鲁棒性,在噪声较大的时候无法取得理想的效果。
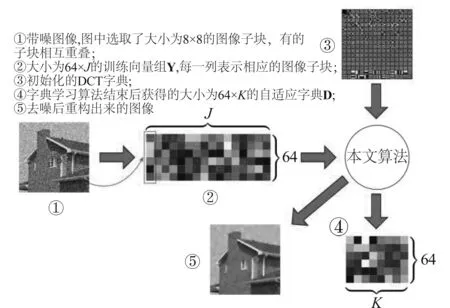
图2 图像去噪实验流程示意图
本文提出算法中有许多参数需要设置,在σ=25噪声的情况下,设置的目标函数的正则化参数为λd=0.38,用于控制λ变化的常数ε设置为0.048,稀疏编码阶段的迭代次数Ks设置为10,字典更新阶段的迭代次数Kd设置为200,用于控制梯度下降法步长的ρ设置为0.001。
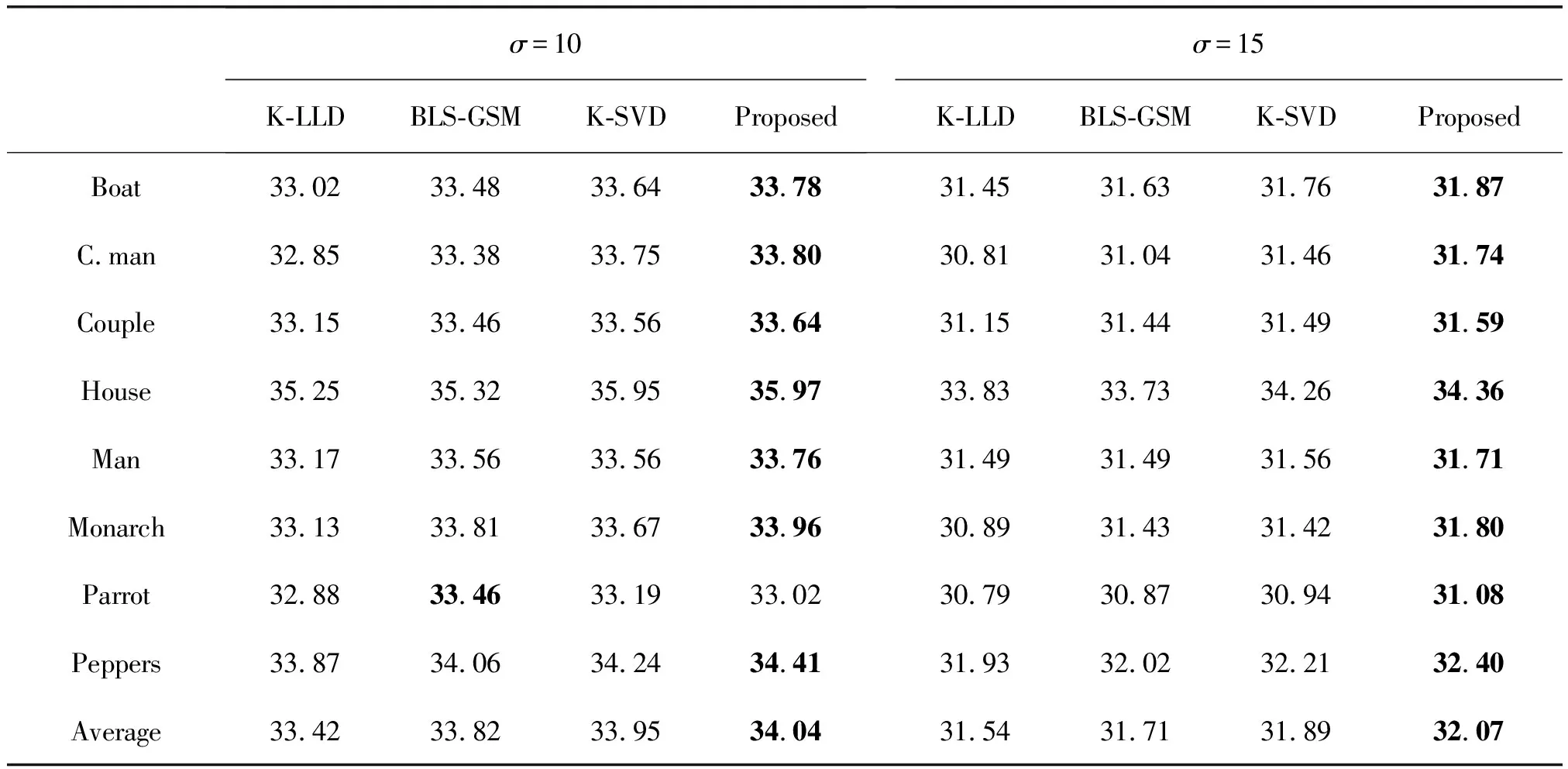
表2 σ=10与σ=15时恢复图像的 PSNR 值对比.其中最好的结果以加粗的形式标记出来.最后一行是对所有图像的去噪结果取平均值
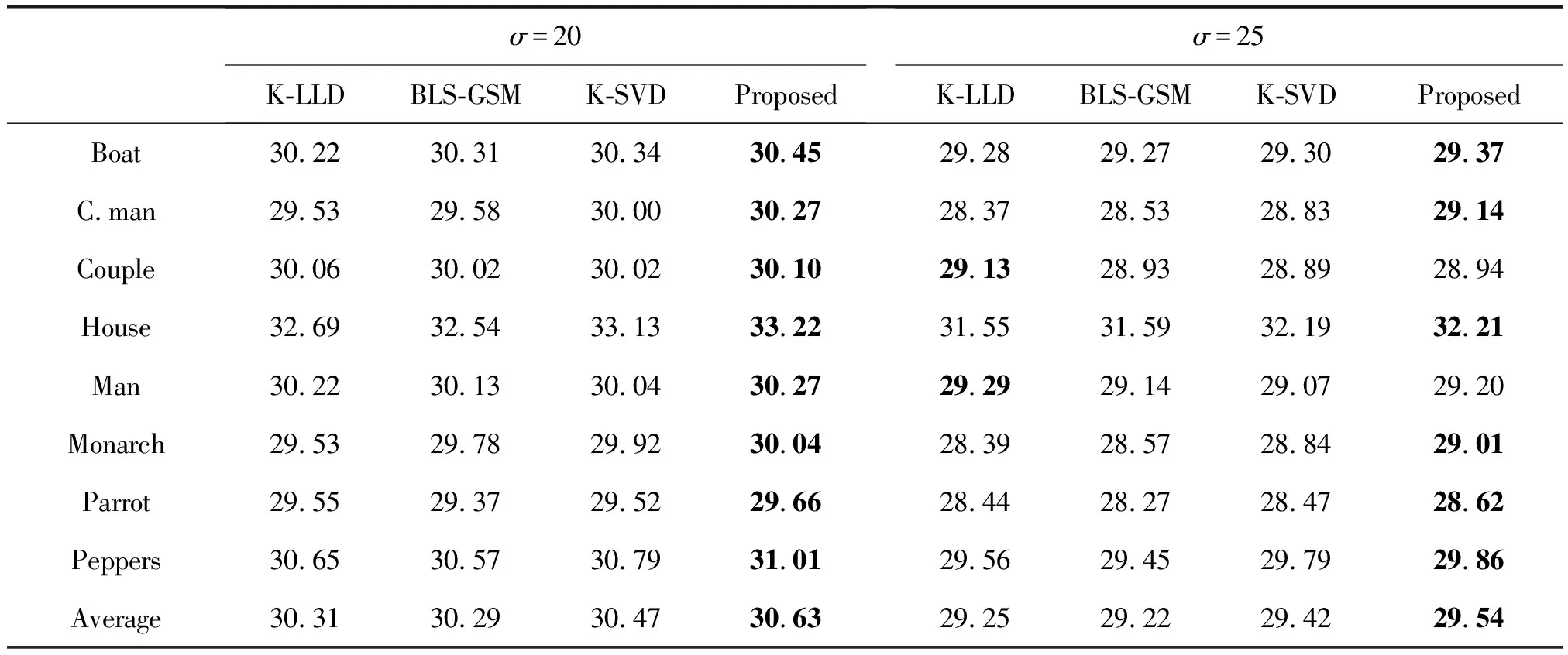
表3 σ=20与σ=25时恢复图像的PSNR值对比
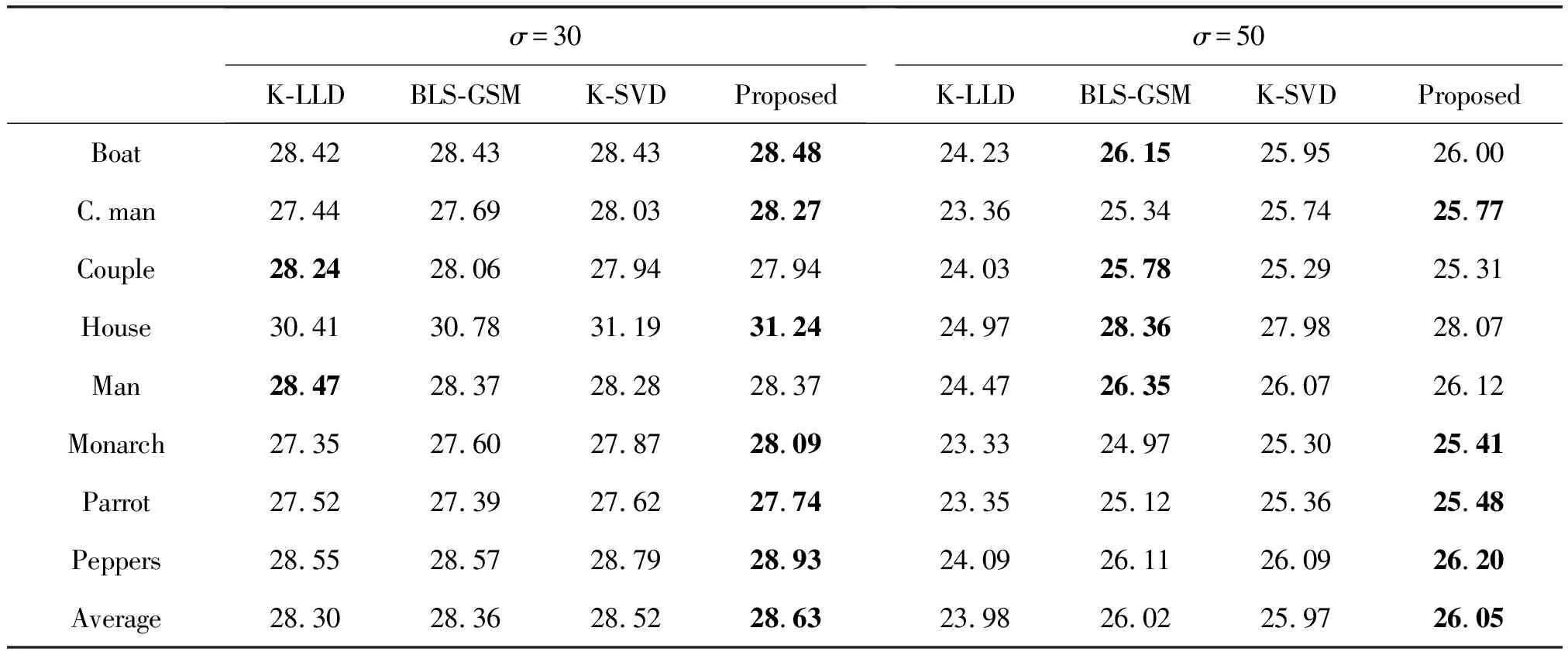
表4 σ=30与σ=50时恢复图像的PSNR值对比
4.2 实验结果与分析
本节将该算法用于标准图像的去噪,得到实验结果并加以分析。本文在CPU 为 Intel i5- 4590, 主频为3.3 GHz,内存为16 G的电脑上,使用Matlab R2015b编程实现了本文的算法。
首先将四种算法分别用于Cameraman、Peppers等8张经典的标准测试图像的去噪,进行多次实验得到相应的实验结果,并将去噪后图像的PSNR值汇总于表2、表3与表4中。
从表2、表3与表4中可以看出,在不同的噪声等级下,相对于其他三种算法,本文方法得到的PSNR值明显较高。这说明本文算法具有较好的去噪效果。比如σ=25时,本文方法在大多数测试图像的PSNR都高于其他三种算法,在Cameraman 图上的去噪结果甚至可以比K-SVD算法的结果高出0.3 dB;在σ=50这样的强噪声情况下,本文方法依然可以取得不俗的效果。同时可以从表中看出,使用了字典学习方法(K-SVD 和本文提出的方法)进行图像去噪得到的效果,在不同的图像都可以取得比较好的效果,而使用固定字典的方法(BLS-GSM)在有些图可以取得比较好的效果,但是在其他图像上取得的PSNR值明显低于K-SVD和本文方法。比如σ=25的House图, K-SVD算法和本文方法取得的PSNR 值相比BLS-GSM算法提高了0.5 dB以上。而K-LLD算法不同于K-SVD算法和本文的算法,它不仅仅有字典学习的步骤,还针对图像结构使用了K-means聚类的方法,然而K-means对于初始值和噪声没有很好的鲁棒性,因此在噪声较大(σ=50)的情况下,K-LLD 算法无法取得理想的去噪效果。
从表3与表4中还可以看出,在部分情况下本文算法的去噪性能略低于其他对比算法。比如在噪声为σ=50的情况下,BLS-GSM 算法在部分图像上去噪效果高于本文算法。这是因为在训练字典时本文算法并没有选取图像中全部的图像子块作为训练集,在噪声较大的时候,学习得到的字典可能并没有获取图像中足够的结构纹理信息,因此导致去噪的效果降低。KSVD 和 KLLD 算法在学习字典时也采取类似的策略,可以有效地提升算法的速度。为了公平地和上述算法进行对比,本文算法在训练字典时并没有利用全部的图像子块。
图3展示了四种算法对带噪的Cameraman图(σ=25)的去噪效果对比。从图3中可以看到本文方法取得的结果图像里“毛刺”更少,图像细节更清晰,主观视觉效果更好。
正如前文所叙述的,同伦算法相对其他算法的主要优势就在于,在较大的数据里进行学习的时候可以更快的收敛。因此,下面比较了本文提出的方法和经典的K-SVD算法在收敛速度上的不同。
图4中展示了本文算法和K-SVD算法对σ=50的House图进行去噪的收敛速度的比较结果。从图中可以看出,本文算法仅仅在30 s以内就达到收敛,而K-SVD则需要超过60 s才能收敛,说明本文算法在收敛速度上具有较大的优势。
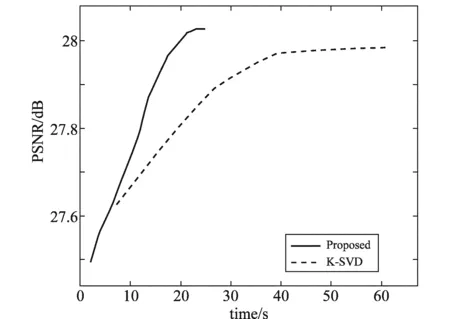
图4 本文算法与K-SVD 算法对σ=50的House图去噪的收敛速度比较
5 结论
本文在深入研究稀疏表示理论和字典学习理论的基础上,提出了一种新的图像去噪算法。算法主要分为两个部分,分别是字典学习和图像去噪模型的建立。本文算法使用同伦方法学习字典,将字典学习阶段获得的自适应字典用于图像去噪模型中,实现图像去噪的目的。在实验的结果中,本文比较了K-LLD算法、BLS-GSM算法、K-SVD算法以及本文算法对标准测试图像的去噪结果,结果显示在不同的噪声等级下,本文算法的PSNR值明显较高,说明本文算法具有较好的去噪效果;同时在比较字典学习算法(比如K-SVD算法和本文算法)与使用单一固定字典的BLS-GSM算法的PSNR值可以看出,使用自适应字典在图像去噪上更具优势。在关于K-SVD算法和本文算法收敛速度比较的实验中,从实验结果可以看出本文算法相对K-SVD算法在收敛速度上有非常大的提升,同时去噪的结果也更好,说明使用同伦方法学习字典具有收敛速度快且信号恢复的准确度高等优点。
[1] Engan K, Aase S O, Hakon H J. Method of optimal directions for frame design[C]∥IEEE International Conference on Acoustics,Speech, and Signal Processing,1999:2443-2446.
[2] Aharon M, Elad M, Bruckstein A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311- 4322.
[3] Cai Shuting, Weng Shaojia, Luo Binling, et al. A dictionary-learning algorithm based on method of optimal directions and approximate K-SVD[C]∥2016 35th Chinese Control Conference, 2016: 6957- 6961.
[4] Raja H, Bajwa W U. Cloud K-SVD: A Collaborative Dictionary Learning Algorithm for Big, Distributed Data[J]. IEEE Transactions on Signal Processing, 2016, 64(1): 173-188.
[5] Dumitrescu B, Irofti P. Regularized K-SVD[J]. IEEE Signal Processing Letters, 2017, 24(3): 309-313.
[6] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2006, 15(12): 3736-3745.
[7] Liu Zhou, Yu Lei, Zhang Menglei, et al. Nonlocal structured nonparametric Bayesian dictionary learning for image denoising[C]∥2016 IEEE 13th International Conference on Signal Processing, 2016: 144-148.
[8] Asif M S. Dynamic Compressive Sensing: Sparse Recovery Algorithms for Streaming Signals and Video[D]. Georgia Institute of Technology, 2013.
[9] Asif M S, J. Romberg. Fast and Accurate Algorithms for Re-Weighted L1-Norm Minimization[J]. IEEE Transactions on Signal Processing, 2013, 61(23): 5905-5916.
[10] Asif M S, Romberg J. Dynamic Updating for L1 Minimization[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 421- 434.
[11] Niknejad M, Sadeghi M, Babaie-Zadeh M, et al. A Dictionary Learning Method for Sparse Representation Using a Homotopy Approach[C]∥Latent Variable Analysis and Signal Separation: 12th International Conference, 2015: 271-278.
[12] Smith L N, Elad M. Improving dictionary learning: Multiple dictionary updates and coefficient reuse[J]. IEEE Signal Processing Letters, 2013, 20(1): 79- 82.
[13] Wright S J. Sparse reconstruction by separable approximation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2479-2493.
[14] Pati Y C. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]∥1993 Conference Record of The Twenty-Seventh Asilomar Conference on Signals, Systems and Computers, 1993:40- 44.
[15] Chatterjee P, Milanfar P. Clustering-based denoising with locally learned dictionaries[J]. IEEE Transactions on Image Processing, 2009, 18(7): 1438-1451.
[16] Portilla J, Strela V. Image denoising using scale mixtures of Gaussians in the wavelet domain[J]. IEEE Transactions on Image Processing, 2003, 12(11): 1338-1351.

