降噪多天线卫星导航欺骗干扰抑制方法
王 纯 郝鹏飞 张林让
(1. 西安建筑科技大学信息与控制工程学院,陕西西安 710055;2. 西安电子科技大学电子信息工程学院,陕西西安 710071)
1 引言
尽管传统阵列天线技术是卫星导航对抗压制干扰最为有效的方法之一[1-2],但当卫星导航欺骗干扰源发射比真实信号功率稍大的假信号时,欺骗干扰对抗效果欠佳。如最小方差无失真响应(MVDR)、广义旁瓣相消(GSC)和功率倒置法(PI)等为代表的常规自适应空域滤波均是GPS接收机阵列天线对抗大功率压制干扰的常规算法。但阵列天线卫星导航接收机在欺骗干扰环境中面对低SNR和负JNR,阵列接收信号协方差矩阵的逆与真实信号导向矢量不正交,故无法抑制欺骗干扰。
目前,世界各国研究机构学者已纷纷将研究重心转向卫星导航接收终端反欺骗技术,该技术已出现在许多公开发表的文献中。加拿大卡尔加里大学Daneshmand[3]提出了低计算复杂度的阵列天线抗欺骗干扰方法,该方法提取欺骗的导向矢量时没有要求对阵列接收信号解扩。随后,2014年提出一类预解扩的阵列天线GPS抗欺骗干扰方法,它基于正交投影和解扩实现欺骗干扰抑制[4]。该方法通过干扰的正交投影矩阵对接收数据进行投影,再对投影后的数据进行解扩,最后根据最大信噪比准则求权。后来,两级结构压制和欺骗干扰联合抑制方法成功利用两次正交投影逐级实现了对压制干扰和欺骗干扰的抑制,并避免了预解扩带来的计算复杂度[5]。与此同时,一种低复杂度盲欺骗干扰抑制方法——互相关投影法首先设法求得干扰正交投影矩阵,再利用投影互相关矩阵进行的最大特征值对应的特征向量实现欺骗干扰抑制[6]。然而,这些方法均未阐明对传统阵列天线抑制在欺骗干扰环境中性能不佳的直接原因。本文以MVDR空域滤波算法为例,从欺骗干扰环境中信噪比、干噪比、信干比等参数对输出信干噪比的影响入手,特别是信号和干扰强度远小于噪声强度的情况。当干扰导向矢量与噪声子空间正交时,阵列在干扰方向上才可以形成零陷[7- 8]。但从MVDR算法的输出功率表达式上看,噪声功率较高时会退化成为常规波束形成(CBF)[9-11],故只能对期望信号方向保型,而不能对干扰方向产生零陷,就不具备欺骗干扰抑制的能力了。
本文首先通过降噪改善卫星导航阵列接收环境,在使用输出功率最小准则最优化权矢量时,保留了协方差矩阵逆的小特征值对应的特征向量,使之与真实信号导向矢量正交,从而保证对欺骗干扰方向上形成零陷,成功实现欺骗干扰的抑制。此外,本文从理论上分析了降噪欺骗干扰抑制方法在协方差矩阵的影响,以及该方法的波束方向图和输出SINR性能。最后,仿真实验验证所提方法能有效抵抗欺骗干扰的攻击。
2 信号模型
假设接收机前端放置了N根间距半波长等距线阵,接收M个信号,其中包括P个真实信号和Q个欺骗干扰,以及加性高斯白噪声。经过单路径传播后,M个阵元接收的信号向量x(t)可以表示为:
(1)
式中,a(θi)为第i个导航卫星的导向矢量,a(θk)为第k个欺骗干扰的导向矢量,而n(t)为加性高斯白噪声。bi(t)为数据比特;ci是第i个导航卫星的扩频码。Pi表示第i个卫星的总发射功率,令θi、τi分别是第i个卫星信号到达接收天线阵列的波达方向、时延。此时,设i=1上式可写作:
x(t)=σ1b1(t-τ1)c1(t-τ1)ejφa1+j(t)+n(t)
(2)
(3)
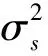
对接收信号协方差矩阵Rx做特征值分解得
(4)

(5)
可以看出,此时无法利用小特征值对应的特征向量ui(i=M+1,M+2,…,N)与导航信号导向矢量的正交关系,因此波束方向图无法在干扰相应位置形成零陷。从另一方面说,在欺骗干扰和压制干扰这两种背景下,干扰信号功率水平的不同是接收环境最主要的区别:1)压制干扰功率与噪声功率的比值(即干噪比INR)约20 dB甚至更大;2)欺骗干扰环境下的INR仅-15 dB左右,远小于前者。
3 降噪预解扩欺骗干扰抑制方法

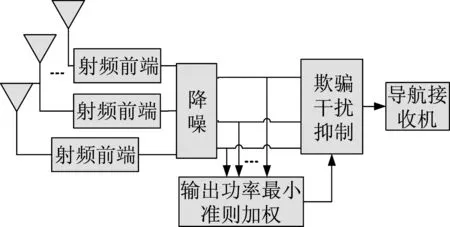
图1 所提方法框图
3.1 降噪预处理
(6)
(7)
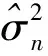
x1(t)=σsb1(t-τ1)c1(t-τ1)ejφa1+j(t)+α·n(t)
(8)
其中,系数α表示降噪系数,其范围0≤α≤1,α越大,说明降噪程度不明显;α越小,说明降噪程度越严重。α·n(t)可以看做是降噪后接收信号中的残留噪声成分。
降噪后的接收信号协方差矩阵为
(9)
结合式(7)所示的降噪过程,可以算得降噪系数α的值为
(10)
在非常理想的情况下,噪声功率估计值与真实值越接近,α越接近零,此时降噪后的接收信号x1(t)中几乎不含噪声成分。
3.2 降噪预处理后的最优化波束形成
设权矢量为w,则降噪后阵列输出为
y(t)=wH·x1(t)
(11)
阵列总的输出功率为
Pout=E[|y(t)|2]=wHRx1w
(12)
求取最优加权矢量时根据带约束的输出功率最小准则,即在保证对真实信号的增益为常数wH·a1=1的条件下,使输出总功率最小。
(13)
式中a1表示期望信号的导向矢量。利用拉格朗日乘子法构建代价函数,求极值可得加权矢量为
(14)

4 降噪处理对协方差矩阵的影响分析
δ1≥δ2≥…≥δM≥δM+1=δM+2=…=δN=
(15)
(16)

5 降噪欺骗干扰抑制方法的性能分析
下面分析降噪欺骗干扰抑制方法在方向图和输出SINR的性能。
5.1 方向图性能分析
采用降噪欺骗干扰抑制方法的加权矢量,计算阵列方向图表达式为
(17)
分析此算法下的阵列方向图:
(1)在GPS真实卫星信号的来波方向上,a(θ)=a1,阵列的方向图响应为
(18)
由此可见,降噪欺骗干扰抑制方法下,阵列对GPS真实卫星信号的增益为单位增益,算法可以保证对真实卫星信号的无失真接收。
(2)该方法考虑到降噪后的数据其噪声子空间内的特征向量ui(i=M+1,M+2,…,N)与干扰导向矢量之间存在正交关系,即
(19)
由于在干扰θk方向上,a(θ)=ak阵列增益为
(20)
此时,阵列波束方向图在干扰方向上的增益可以近似为“0”,说明降噪欺骗干扰抑制方法成功抑制干扰。
5.2 输出SINR性能分析
下面分析降噪欺骗干扰抑制方法的输出信干噪比SINR。将降噪后接收信号协方差矩阵Rx1表达式(9)代入阵列的总输出功率表达式(12)中
(21)
结合前面对算法方向图的分析,在GPS真实信号来向的响应为单位增益,即wHa1=1;在欺骗干扰信号来向上产生零陷,可近似认为wHak=0(k=2,3,...,M)。那么此时阵列总的输出功率
(22)
阵列的输出信干噪比为
(23)

6 仿真及性能分析
为了验证该算法的有效性,主要考察欺骗干扰抑制的波束方向图、GPS同步和输出信干噪比(SINR)这三个方面。设GPS接收机阵列采用半波长均匀间距放置的8阵元线阵。接收机时域采样频率采用奈奎斯特采样频率。信号其中心频率为1.25 MHz,采样频率为5 MHz。期望卫星发射导航信号为粗/截获码(C/A code),在阵列天线GPS接收机中,为了验证本文提出方法的有效性,仿真首先观察了本方法的波束方向图。GPS真实卫星信号功率为-160 dBW,入射角度为-5°,两个欺骗干扰均发送具有同颗卫星的C/A码,延迟随机产生,其功率-150 dBW,入射角度分别为-50°和30°,高斯白噪声的功率为-140 dBW。数据长度选择包括20组1023码长的C/A码。
实验1波束方向图
在上述实验条件下,对比传统MVDR算法和降噪欺骗干扰抑制方法的方向图。如图2所示,降噪欺骗干扰抑制方法的方向图在真实信号方向上为单位增益,且在两个欺骗干扰方向上形成了零陷。说明降噪欺骗干扰抑制方法已恢复了抑制欺骗干扰的能力。
实验2干扰抑制后同步结果
实验考察了使用本文方法后接收机关于频率和码相位的二维捕获结果。从图3可以看出,接收机不受欺骗干扰的影响,可实现对期望卫星的码捕获和多普勒频移捕获。
实验3不同干扰功率对欺骗干扰抑制方法输出SINR的影响
不同干扰功率情况下,对比了降噪欺骗干扰抑制方法与传统MVDR的SINR。仿真实验条件同上,当干扰功率从-170 dBW到-110 dBW变化,采用200次蒙特卡洛实验。如图4所示,降噪欺骗干扰抑制方法在不同干扰功率情况下对输出信干噪比的影响很小,与式(23)结论相符。降噪欺骗干扰抑制方法的输出信干噪比高于传统MVDR算法约20 dB,较大提高了多天线导航接收机抑制欺骗干扰的能力。此外,对大功率欺骗干扰依然有效。

图2 波束方向图的比较

图3 干扰抑制后多普勒频率和码相位二维捕获结果图
实验4不同噪声功率对欺骗干扰抑制方法输出SINR的影响
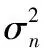
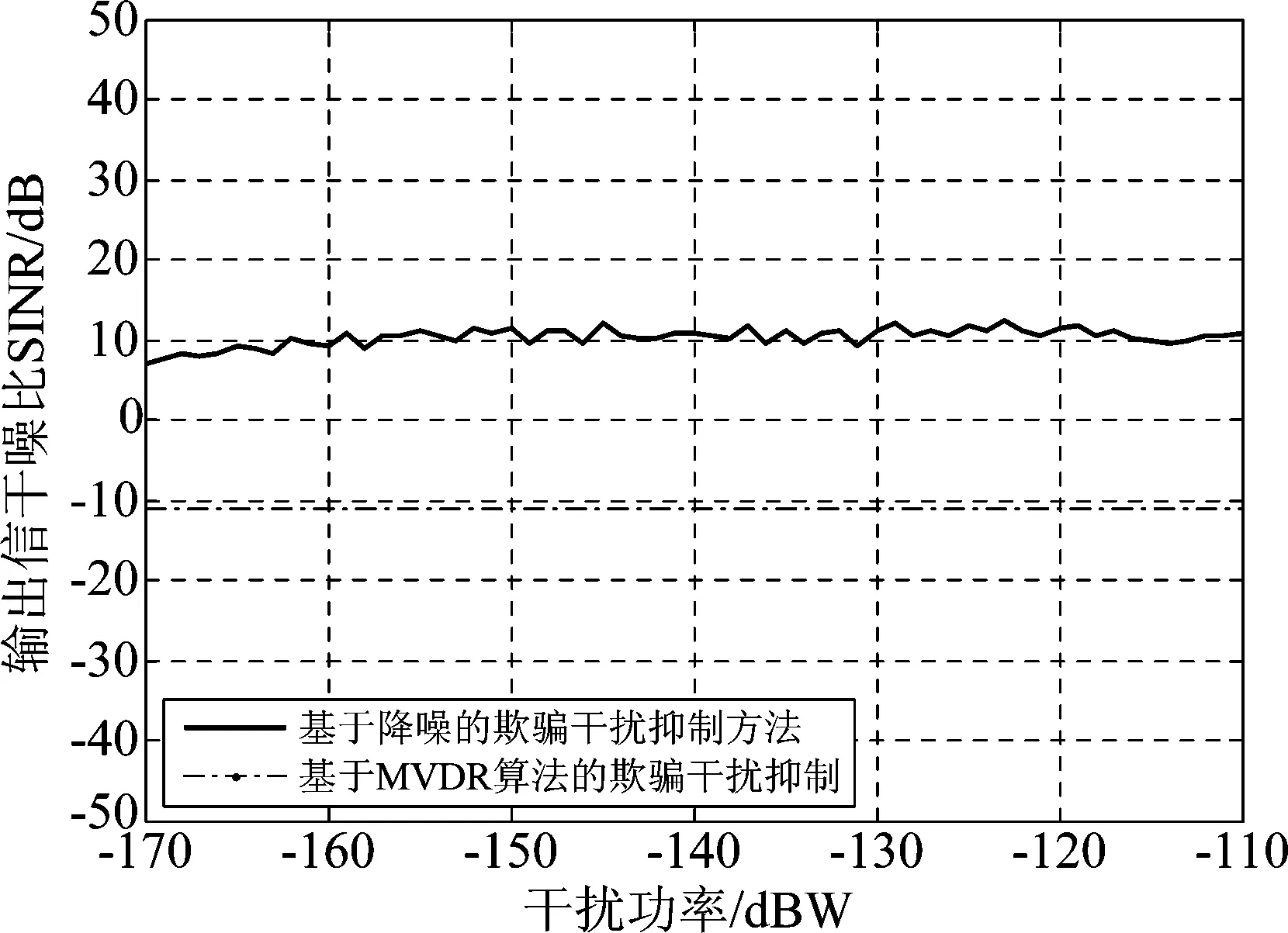
图4 不同干扰功率下输出信干噪比的比较

图5 不同噪声功率下的输出信干噪比的比较
7 结论
在欺骗干扰环境下,干扰和真实信号的功率均远小于噪声功率,致使接收信号协方差矩阵的大、小特征值相差无几,无法将协方差矩阵的逆矩阵近似表达成只含噪声子空间内向量的形式。在运用传统空域自适应滤波方法前,先进行降噪预处理,增加大、小特征值之间的差距,就可以再次将协方差矩阵的逆矩阵近似表达成只含噪声子空间内向量的形式,从而恢复传统空域自适应滤波方法的适用条件。该降噪多天线欺骗干扰抑制方法输出SINR较高,能使接收机不受欺骗干扰影响完成正常捕获工作。
[1] 王文益, 杜清荣, 吴仁彪, 等.一种利用少快拍数据的卫星导航高动态干扰抑制算法[J].电子与信息学报,2014, 36(10): 2445-2449.
Wang W Y, Du Q R, Wu R B, et al. High Dynamic Interference Suppression Based on Few Snapshots for Satellite Navigation System[J]. Journal of Electronics & Information Technology, 2014, 36(10): 2445-2449.(in Chinese)
[2] 张柏华, 马红光, 孙新利,等.基于正交约束的导航接收机空时自适应方法[J].电子与信息学报, 2015, 37(4): 900-906.
Zhang B H, Ma H G, Sun X L, et al. Space Time Adaptive Processing Technique Based on Orthogonal Constraint in Navigation Receiver[J]. Journal of Electronics & Information Technology, 2015, 37(4): 900-906. (in Chinese)
[3] Daneshmand S, Jahromi A, Broumandan A, et al. A Low-Complexity GPS Anti-Spoofing Method Using a Multi-Antenna Array[C]∥Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville TN, 2012, 137(1):1233-1243.
[4] Daneshmand S, Jafarnia-Jahromi A, Broumandan A, et al. A GNSS structural interference mitigation technique using antenna array processing[C]∥Sensor Array and Multichannel Signal Processing Workshop (SAM), 2014 IEEE 8th, 2014: 109-112.
[5] 包莉娜, 吴仁彪, 王文益,等. 两级结构的卫星导航压制式和欺骗式干扰联合抑制算法[J]. 信号处理, 2015, 31(9):1041-1046.
Bao L N, Wu R B, Wang W Y, et al. Two-step GPS Interference Suppression Algorithm for Spoofing and Jamming[J]. Journal of Signal Processing, 2015, 31(9): 1041-1046. (in Chinese)
[6] 王纯, 张林让. 基于互相关投影导航接收机欺骗干扰抑制方法[J]. 电子与信息学报, 2016, 38(8):1984-1990.
Wang C, Zhang L R. Spoofing Mitigation Method for Navigation Receiver Based on Cross Correlation and Projection[J].Journal of Electronics & Information Technology, 2016, 38(8):1984-1990. (in Chinese)
[7] Wax M, Anu Y. Performance analysis of the minimum variance beamforming[J]. IEEE Transactions on Signal Processing, IEEE, 1996, 44(4): 928-937.
[8] 王永良, 丁前军, 李荣峰. 自适应阵列处理[M]. 北京: 清华大学出版社, 2004:30-36.
Wang Y L, Ding Q J, Li R F. Adaptive array processing[M].Beijing:Tsinghua University Press,2004:30-36.(in Chinese)
[9] Araki S, Okada M, Higuchi T,et al. Spatial correlation model based observation vector clustering and MVDR beamforming for meeting recognition[C]∥2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, 2016: 385-389.
[10] Sergiy A. Vorobyov. Principles of minimum variance robust adaptive beamforming design[J]. Signal Processing, 2013,93(12): 3264-3277.
[11] Amin M G, Closas P, Broumandan A, et al. Vulnerabilities, Threats and Authentication in Satellite-Based Navigation Systems[C]∥Proceedings of the IEEE, 2016, 104(6): 1169-1173.

