结合波利亚罐模型和M-H算法的遥感图像分割

李 玉 李 杰 王 玉 赵泉华

(辽宁工程技术大学测绘与地理科学学院遥感科学与应用研究所，辽宁阜新 123000)

1 引言

图像分割是根据图像像素的一些特殊性质(如光谱测度、空间结构特征等)，按照某种规则或算法将图像分成具有一致特性区域的方法和手段[1]，是遥感图像处理中的关键技术，也是对图像后续分析的基础。至今，图像分割已经有多种相关方法[2]，主要包括：阈值分割[3]、区域分割[4]、聚类分割[5]和统计模型分割[6]。然而，随着遥感成像技术的快速发展，遥感图像分辨率逐渐提高，增加了其分割的困难性。目前，很多针对低、中分辨率遥感图像的分割方法已无法满足在实际应用中对分割精度的要求。因此，如何对遥感图像进行精确分割愈加受到关注。

由于分辨率的提高，遥感图像细节信息愈加丰富，而目前的图像分割方法多是以单一像素作为处理单元，没有利用像素之间存在的相关性，使用这种传统的分割方法得到的结果中必会包含较多错分像素[7]。因此，如何有效利用像素之间关系成为遥感图像分割中的关键问题。对此，Hassner和Sklansky[8]将马尔科夫随机场(Markov Random Field, MRF)引入图像分割中，为像素及其邻域的相互关系提供一种描述方式，使得有效利用像素之间的关系成为可能。在基于MRF的图像分割方法中，常用Potts模型定义邻域势能函数[9]。Potts模型将图像看作像素阵列，像素类别表示模型的状态，阵列中任意像素的状态由该像素的邻域像素状态决定。该模型原理简单，普适性强，可有效将像素邻域运用到图像分割中。然而，Potts模型是将中心像素与其邻域内像素逐个进行对比，仅考虑邻域内单个像素对中心像素的作用，未考虑邻域整体的作用。因此，该模型抗噪性不强[10]，容易造成中心像素错分，尤其体现在处理较复杂的图像中。为此，本文在波利亚罐模型的基础上，试图定义新的邻域势能函数，该函数将邻域整体作为处理单元，从而达到减少像素错分、提高抗噪性的效果，进而有效提高图像分割精度。

波利亚罐模型是由Polya和Eggenberger[11]为模拟传染病在人群中的扩散提出的一种随机实验模型，该模型包含许多重要的概率分布，在概率论和应用概率中占有十分重要的地位[12]。波利亚罐模型实验对罐中不同颜色的小球进行随机抽取，每次取出一个小球，记录颜色后放回，然后加入一些同样颜色的小球，以这样的过程模拟传染病的扩散。此过程每进行一次，罐中小球的组成会发生变化，随着抽取次数的增加，被取到次数最多的某颜色小球在罐中的数量会逐渐增多。Polya和Eggenberger根据这种随着抽取次数增加，某颜色小球数量逐渐增多的现象，提出模型的“时间传染”特性。在Johnson和Kotz[13]的研究中，发现波利亚罐模型的随机实验过程可以生成马尔科夫链和马尔科夫随机场。在图像处理领域，Alajaji和Burlina[14]根据该模型提出一种能够去除噪声的图像重建方法；耿茵茵等[15]则提出了一种区分图像前景和背景的判决机制，并应用于指纹图像处理中；Banerjee等[16]将该模型应用到图像分割中，根据模型的“空间传染”特性，得到一种有效提高图像分割精度的处理方法，但该方法在针对纹理特征比较复杂的区域上依然存在误判问题。

本文将波利亚罐模型应用到遥感图像分割中，根据该模型为图像标号场定义一新的邻域势能函数，在此基础上结合Bayesian定理，构建图像统计分割模型，并根据最大后验概率(Maximum A Posteriori, MAP)准则[17]和Metropolis-Hastings(M-H)算法[18-19]求解分割模型。分别对模拟图像与真实遥感图像进行分割实验，验证提出方法的可行性和有效性。

2 算法描述

2.1 波利亚罐模型

罐模型是一种随机实验模型，根据预先设计的方案，抽取罐中不同颜色的小球，根据取到小球的颜色改变罐中各颜色小球的数量，从而改变罐中各颜色小球的组成，这样的随机实验模型为罐模型[20]。

波利亚罐模型是一种重要的罐模型。假设罐中有B个蓝色小球和W个白色小球，从中随机抽取一只，记录颜色后放回，并加入c个相同颜色的小球。每次抽取后，取出的某颜色小球(如蓝色小球)数量增加，而另一种颜色小球(如白色小球)数量不变。上述过程重复进行，直到满足预设的终止条件，这种随机实验模型称为波利亚罐模型。以下是该模型的一些基本性质和推论。

性质1设事件Bn为第n次抽取取到蓝色小球，由数学归纳法可得到Bn发生的概率P(Bn)为：

(1)

上式表明，每次抽取到蓝色小球的概率只与B和W相关，等于B/(B+W)，即最初罐中蓝色小球与所有小球的数量比。

性质2以Xn表示前n次抽取中取到蓝色小球的次数，P(Xn=k)表示这n次抽取中取到蓝色小球次数为k的概率，则P(Xn=k)为：

(2)

其中，H=B+W，表示抽取前罐中蓝、白两种颜色小球的总个数。式(2)分子分母同除以c，并令α=B/c，γ=W/c，H/c=α+γ，得到该式的另一种表达方式，即：

(3)

其中，〈α〉k=α(α+1)…(α+(k-1))，〈γ〉n-k=γ(γ+1)…(γ+(n-k-1))，〈α+γ〉n=(α+γ)(α+γ+1)…(α+γ+(n-1))。

推论由式(3)可得前n次抽取过程中，取到蓝色小球次数的期望E(Xn)为：

(4)

设Yn表示n次抽取后罐中蓝色小球的总个数，则Yn=cXn+B，E(Yn)表示n次抽取后罐中蓝色小球总个数的期望，由Yn及E(Xn)可得E(Yn)：

(5)

可得出n次抽取后罐中蓝色小球所占比例P(Yn)：

(6)

上式表明，n次抽取后罐中蓝色小球数与小球总数比等于最开始时罐中蓝色小球数与小球总数之比。因此，若抽取前罐中某颜色(类别)小球数量占优，经过若干次抽取后，该颜色(类别)小球仍然占优，体现了波利亚罐模型随机实验过程具有保持罐中小球主要类别的特点。

将上述随机实验过程作用于图像像素邻域，可以强调邻域像素中的主要类别，针对图像中孤立的错分像素，可以根据邻域将其去除，从而更精确地分割图像。

2.2 图像分割模型

设X和Y是两个离散随机场，分别表示为X={Xi1Xi∈L,i∈S}，Y={Yi1Yi∈D,i∈S}，其中，Xi和Yi分别为X和Y中的元素，取值范围分别为L和D。L、D和S表示三个符号集：L={1, …,L}，D={1, …,D}，S={1, …,S}，i表示随机场中元素的索引。在基于像素的图像分割模型中，令离散随机场X和Y分别表示图像的标号场和特征场，Xi和Yi分别为像素i对应的随机变量；符号集L和D分别表示图像类别的集合和图像光谱测度的集合，L和D分别为图像类别总数和图像最大光谱测度；S表示图像域，i为图像像素索引，S为图像像素总数。对于给定图像y={yi1yi∈D,i∈S}，可视为特征场Y的一个实现，yi为像素i的光谱测度。

2.2.1罐模型建立

将波利亚罐模型与图像标号场相结合，根据邻域建立罐模型。将像素i视为罐，初始形式用u0(i)表示，像素各类别对应小球的各颜色，u0(i)中各颜色小球数由像素i的邻域中各类别像素的个数得到。对具有L个目标类的图像建立罐模型，设Gl,0(i)表示抽取前(即0次抽取后)类别标号为l的小球数量，Gl,0(i)根据像素i的邻域得到，此过程可由图1表示。

图1 像素i邻域标号场及其初始罐模型u0(i)

图1表示可分割为3个类属(L=3)的遥感图像，结合邻域像素标号，为中心像素i建立罐模型的过程。图中像素i邻域中有3个标号为1的像素，2个标号为2的像素，3个标号为3的像素。令罐中黑、灰、白三色分别对应1、2和3三种标号，设罐中初始小球总数H0(i)为8，则像素i的初始罐模型u0(i)中含3个黑色(标号1)小球、2个灰色(标号2)小球、3个白色(标号3)小球，即G1,0(i)=3，G2,0(i)=2，G3,0(i)=3。将以上过程作用于图像中的其他像素，完成罐模型的建立。

u0(i)和H0(i)分别为初始时像素i罐模型和小球总数的表示方式，以此类推，则un-1(i)和Hn-1(i)分别表示第n-1次抽取后，进行第n次抽取前像素i的罐模型及小球总数，n=1,2, …。

2.2.2标号场模型

采用MRF描述图像标号场，并使用波利亚罐模型定义其邻域势能函数。假设标号场X中各随机变量Xi相互独立，根据MRF与Gibbs随机场的等价性[21]，标号场X的概率密度函数为：

(7)

其中，Ni表示像素i的邻域像素集合，i′为Ni中的像素，i′∈Ni；η表示邻域像素的空间作用强度，为预定义参数；Vi′(Xi)为像素i的邻域势能函数，可表示为：

(8)

上式利用波利亚罐模型进行定义，Gl,F(i)和HF(i)分别为第F次波利亚罐模型随机实验过程后，罐中颜色(标号)为l的小球的个数和所有小球总个数，具体过程说明如下：

(1)抽取及成分更新

根据图2所示方法在un-1(i)中模拟波利亚罐模型的随机实验过程。

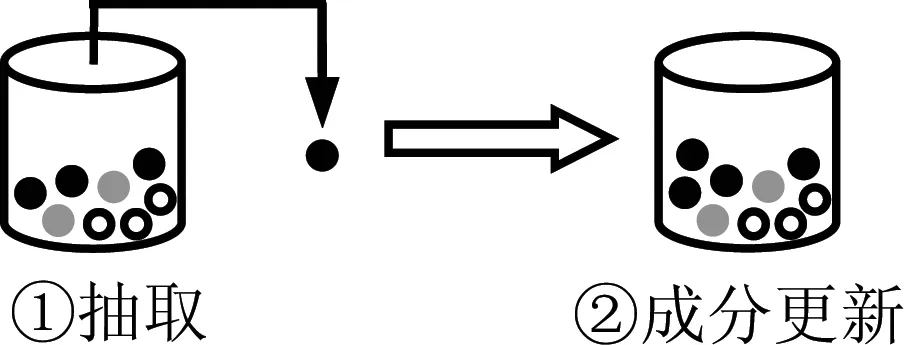
图2 抽取及成分更新过程示意图

图2中，在un-1(i)中使用赌轮盘随机选择方法[22]取出一个小球，假定得到小球的颜色为黑(①)，则向un-1(i)中加入c个黑色(标号1)小球(②，此图中c=1)，得到成分更新后的罐模型un(i)。①中得到的颜色(标号)用Jn(i)表示，则图中Jn(i)为1。

针对分为L类的图像，Jn(i)取值如下：

Jn(i)=l,l=1,…,L

(9)

上式也可表示第n次抽取得到的小球标号为l。然后，向罐un-1(i)中加入c个标号为l的小球，得到罐un(i)，此过程可表示如下：

un(i)={Gl,n(i),Gl′,n(i)1l,l′=1,…,L,

l≠l′,n=1,2,…}

(10)

其中，如果Jn(i)=l，则Gl,n(i)=Gl,n-1(i)+c，Gl′,n(i)=Gl′,n-1(i)。

重复上述过程，若达到规定的抽取次数，或者罐un(i)中各颜色小球数量比与罐un-1(i)中对应颜色小球数量比基本一致，停止抽取。假设停止时总共抽取了F次，则有：

uF(i)={Gl,F(i)1l=1,…,L,F=1,2,…}

(11)

(2)邻域势能函数

根据上述随机实验过程，结合该过程相关性质，得到利用波利亚罐模型定义的邻域势能函数，即式(8)。将该式代入式(7)，得到最终标号场X的概率密度函数：

(12)

2.2.3特征场模型

若像素i的标号Xi=l，则假设其特征变量Yi服从参数为μl和σl的高斯分布，且所有像素相互独立。由此，得到Y的联合条件概率密度函数：

(13)

其中，p(Yi1Xi=l,θl)为给定标号Xi=l条件下，特征变量Yi的概率密度。θ={θl,l∈L}={μ,σ}={μ1, …,μL,σ1, …,σL}表示特征场模型参数矢量，l为类别标号索引，μ为高斯分布均值矢量，σ为高斯分布标准差矢量。

令高斯分布的均值矢量μ(标准差矢量σ)为相互独立的随机变量且满足某种先验分布，假设μ(σ)服从均值为μμ(μσ)，标准差为σμ(σσ)的高斯分布，其联合概率密度函数为：

(14)

(15)

2.2.4后验概率模型

给定的图像y可以作为特征场Y的一次实现，在此条件下可将Y视为已知量。根据Bayesian定理，可得到由标号场X、特征场Y、参数矢量θ={μ,σ}组成的联合后验概率密度函数：

p(X,θ1Y)∝p(X)p(Y1X,θ)p(θ)

=p(X)p(Y1X,θ)p(μ)p(σ)

(16)

上式为建立的统计分割模型，求出该式中的标号场X和参数矢量θ即可实现图像分割。利用MAP准则，标号场X的最优解Xopt可表示为：

Xopt=arg max{p(X,θ1Y)}

(17)

2.3 M-H算法

由MAP准则，当后验概率密度函数最大时，得到最优的图像分割结果，因此需要求出可令p(X,θ1Y)达到最大的Xopt和θopt。由于M-H算法在进行参数求解时原理简单、操作方便，本文利用该方法求解X和θ。为完备采样(X,θ)，设计移动操作：(1)改变参数矢量θ；(2)改变标号场X。具体过程如下：

(1)改变参数矢量θ

(18)

(19)

(2)改变标号场X

从Y={Yi1Yi∈D,i∈S}中以等概率方式随机抽取一像素i，其标号Xi=l；再从L={1,…,L}中以等概率方式随机抽取一标号l*，若l*≠l，则标号l*的接受率aX(Xi=l,Xi=l*)为：

aX(Xi=l,Xi=l*)=

(20)

2.4 算法流程

本文使用波利亚罐模型重新定义图像标号场的邻域势能函数，并利用M-H算法求解图像的后验概率密度函数，提出方法的流程总结如下：

(1)初始化图像标号场X(0)，高斯分布参数矢量θ(0)；

(2)根据X(0)，为图像各像素建立罐模型；

(3)进行波利亚罐模型随机实验，得到Vi′(Xi)；

(4)在t次迭代，执行M-H算法采样总参数矢量(X(t-1),θ(t-1))，求得(X(t),θ(t))；

(5)步骤(3)、(4)重复进行，直至达到预设的循环次数或总参数矢量(X,θ)收敛到稳定值，停止迭代。

3 实验结果和讨论

为验证本文提出方法的可行性和有效性，在Intel Core i7 3.6GHz/4GB内存/MATLAB R2011a环境下对模拟图像和真实遥感图像进行分割实验。

3.1 模拟图像分割

为对提出方法进行定性、定量评价和比较，首先对模拟图像进行实验。模拟图像以尺寸为128×128的图3(a)为模板，其中，①～④表示不同的同质区域。图3(b)是依据图3(a)模板生成的模拟图像，各同质区域内像素相互独立且服从同一高斯分布，各区域分布参数见表1。由表可知，同质区域①～④的标准差依次递增，标准差越大，分割难度越大。利用提出方法对图3(b)进行分割，并与基于传统Potts模型的分割方法(即，利用Potts模型定义邻域势能函数的分割方法)、文献[10]Potts模型的改进方法、文献[16]方法，以及易康软件中的多尺度分割方法的分割结果进行对比分析，验证提出方法的抗噪性及优越性。

图3 (a) 几何模板；(b) 模拟图像

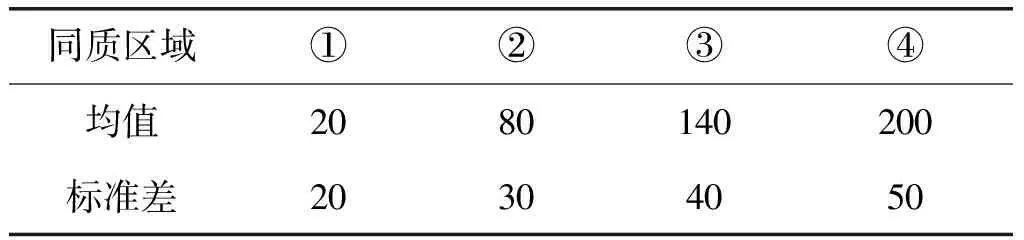
同质区域①②③④均值2080140200标准差20304050

本文采用像素的3×3邻域建立罐模型，实验结果见图4(a)。可以看出，提出方法的分割结果比较理想，能够将各同质区域较好地分割开，各区域内基本不含错分像素。为验证提出方法比基于传统Potts模型的分割方法有更好的抗噪性，对二者的分割结果(见图4(a)和图4(b))进行比较，可以看出，图4(a)各同质区域内的错分像素明显少于图4(b)，说明本文使用波利亚罐模型定义的邻域势能函数抗噪性较强，优于传统Potts模型。图4(c)为文献[10]Potts模型改进方法的实验结果，此方法将中心像素与邻域内各像素的光谱测度值及二者的欧式距离引入势能函数中，以提高抗噪性。图4(c)各区域内错分像素明显减少，优于图4(b)，但没有本文方法实验结果图4(a)理想。此外，波利亚罐模型直接使用邻域整体，而Potts模型是将中心像素与其邻域内像素逐个进行对比，导致后者计算量增加，具体体现在实验运行速度上：图4(a)的运行时间少于图4(b)运行时间的三分之二，少于图4(c)运行时间的四分之三，说明与Potts模型相比，提出方法更方便快捷。图4(d)为文献[16]方法的实验结果，该方法首先对图像进行初分割，在此基础上根据波利亚罐模型的随机实验过程对结果进行优化，以提高图像分割精度。此方法相对方便快捷，但结果的准确性一定程度上取决于图像的初分割结果，局限性过强，且图4(d)各区域内依然存在错分像素和噪声。图4(e)为易康软件多尺度分割方法的实验结果。通过与此结果对比可知，本文方法能够较好地保持各区域边缘。

为对实验结果进行定量精度评价，以图3(a)模板为参考图像，计算图4分割结果的混淆矩阵，并由此矩阵计算用户精度、产品精度、总体精度及Kappa系数，计算结果列于表2。比较表2中五种方法的混淆矩阵和Kappa系数，说明使用提出方法进行分割得到了比较准确的实验结果。图4(a)的总体精度和Kappa系数分别为99.68%和0.9957，高于另外四种对比算法，总体精度和Kappa系数越接近于1，分割结果越准确[23]。上述定量分析结果验证了本文提出方法的抗噪性及优越性。

为了对实验结果进行定性评价，对(图4)提取轮廓线，并将其叠加在模拟图像图3(b)上，如图5所示。可以看出，本文提出方法分割结果轮廓线与实际轮廓线能够较好吻合，且吻合程度优于对比方法。

图4 分割结果((a) 提出方法；(b) Potts模型；(c) 文献[10]方法；(d) 文献[16]方法；(e) 多尺度分割)

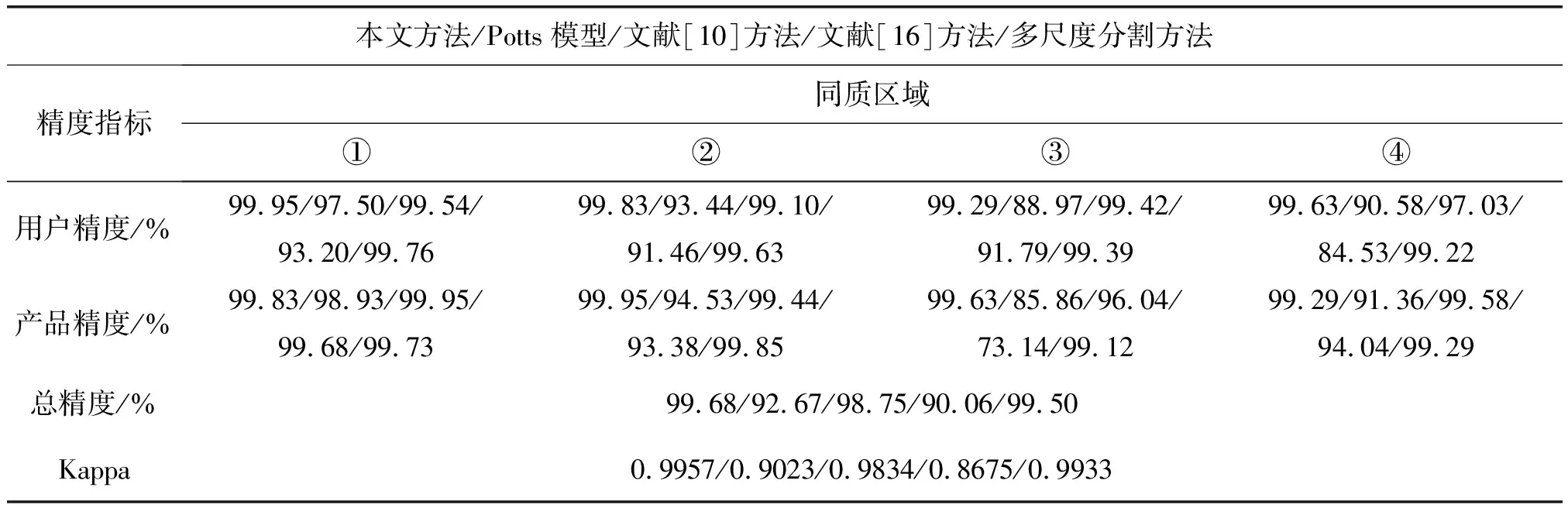
本文方法/Potts模型/文献[10]方法/文献[16]方法/多尺度分割方法精度指标同质区域①②③④用户精度/%99.95/97.50/99.54/93.20/99.7699.83/93.44/99.10/91.46/99.6399.29/88.97/99.42/91.79/99.3999.63/90.58/97.03/84.53/99.22产品精度/%99.83/98.93/99.95/99.68/99.7399.95/94.53/99.44/93.38/99.8599.63/85.86/96.04/73.14/99.1299.29/91.36/99.58/94.04/99.29总精度/%99.68/92.67/98.75/90.06/99.50Kappa0.9957/0.9023/0.9834/0.8675/0.9933

图5 视觉评价((a) 提出方法；(b) Potts模型；(c) 文献[10]方法；(d) 文献[16]方法；(e) 多尺度分割)

3.2 真实遥感图像分割

为验证提出方法的适用性，选取4幅128×128全色遥感图像(如图6)进行分割，类别数分别为2、3、4和4，图像中包含水体、草地、裸地、建筑等常见地物。其中，图6(a)为0.6 m分辨率QuickBird图像，图6(b)为0.5 m分辨率GeoEye-1图像，图6(c)为0.8 m分辨率IKONOS图像，图6(d)为0.7 m分辨率EROS-B图像。对四幅图像分别使用提出方法及四种对比方法进行处理，并对最终结果进行分析比较。

图7(a1)～(d1)为提出方法分割结果，从整体上看，既能够将不同类型地物区分开，又保持了各地物的形状。与传统使用Potts模型及其改进方法的分割结果图7(a2)～(d2)、(a3)～(d3)相比，提出方法各同质区域内的错分像素明显减少。例如，图6(a)中湖泊周边陆地区域中有大量像素和湖泊区域像素灰度接近，图7(a2)和(a3)都没有准确地分割这些像素，使得实验结果陆地区域中有大量的湖泊类，而使用本文方法的图7(a1)可将二者区分开。这是因为提出方法利用波利亚罐模型的随机实验过程，将像素隶属于各类别的概率之间的差距拉大，偏重邻域中像素数量较多的类别，可结合邻域有效去除孤立的错分像素。实验结果图7(b1)～(d1)各区域内的错分像素同样少于图7(b2)～(d2)、(b3)～(d3)，体现了提出方法较Potts模型有更强的抗噪性。此外，图7(a1)～(d1)的运行时间少于图7(a2)～(d2)、(a3)～(d3)，说明提出方法的运行速度更快。通过与文献[16]方法的实验结果图7(a4)～(d4)对比可知，提出方法可以较好保持各地物的形状及细节信息，例如图7(b4)中右上角裸地区域变形，下方黑色线状地物消失，二者在图7(b1)中得到保持。图7(a5)～(d5)为易康软件中多尺度分割方法的分割结果，通过反复实验调整分割尺度参数，使产生的图斑形状尽量与地物形状相吻合，并在最大程度上使类别数与原图一致(四幅图像的形状因子和紧致度因子均设为0.5，尺度参数分别为90、90、95、60)。然而与图7(a1)～(d1)相比，此方法结果中存在类别误判，图7(b5)和(d5)中存在将同类地物分为多类，不同地物分为同类的现象。

为对真实遥感图像分割结果图7进行定量精度评价，以图6的手动标记模板图8为标准分割结果，计算图7的混淆矩阵及各项精度指标，见表3。表3中，图7(a1)～(d1)的各项精度指标都在90%左右，总体精度和Kappa系数均高于另外四种对比算法。通过这些数值，验证了提出方法的准确性和优越性。

图6 真实遥感图像((a) 湖泊；(b) 球场；(c) 海岸；(d) 街区)

图7 分割结果((a1)～(d1) 提出方法；(a2)～(d2) Potts模型；(a3)～(d3) 文献[10]方法；(a4)～(d4) 文献[16]方法；(a5)～(d5) 多尺度分割)

图8 真实遥感图像模板

图9为图7分割结果的视觉评价，从轮廓线与原图像的叠加效果来看，提出方法可以很好地实现分割。

表3 真实遥感图像的定量评价

图9 视觉评价((a1)～(d1) 提出方法；(a2)～(d2) Potts模型；(a3)～(d3) 文献[10]方法；(a4)～(d4) 文献[16]方法；(a5)～(d5) 多尺度分割)

4 结论

遥感图像的精确分割一直是遥感图像处理中的研究热点。为此，本文提出一种结合波利亚罐模型和M-H算法的遥感图像分割方法。提出方法通过模拟波利亚模型可以产生MRF的随机实验过程，为像素及其邻域建立一种相互关系，在此基础上为图像标号场模型定义新的邻域势能函数。此函数根据波利亚罐模型“时间传染”和“空间传染”的特性，可以提高分割方法的抗噪性，从而更精确地分割图像，同时易于求解。采用提出方法分别对模拟图像和全色遥感图像进行分割实验和评价，评价结果验证了该方法的可行性和有效性。此外，波利亚罐模型还有许多性质可以运用到图像分割中，在下一步工作中，主要从提高图像边缘分割精度和可变类图像分割两方面进行研究。

[1] Jensen J R. Introductory Digital Image Processing: A Remote Sensing Perspective(3rd Edition)[M]. Upper Saddle River, United States: Pearson Prentice Hall, 2005: 393-399.

[2] 周莉莉, 姜枫. 图像分割方法综述研究[J]. 计算机应用研究, 2017, 34(7): 1921-1928.

Zhou Lili, Jiang Feng. Survey on image segmentation methods[J]. Application Research of Computers, 2017, 34(7): 1921-1928. (in Chinese)

[3] 吴一全, 孟天亮, 吴诗婳. 图像阈值分割方法研究进展20年(1994-2014)[J]. 数据采集与处理, 2015, 30(1): 1-23.

Wu Yiquan, Meng Tianliang, Wu Shihua. Research progress of image thresholding methods in recent 20 years(1994-2014)[J]. Journal of Data Acquisition and Processing, 2015, 30(1): 1-23. (in Chinese)

[4] 王玉, 李玉, 赵泉华. 可变类多光谱遥感图像分割[J]. 遥感学报, 2016, 20(6): 1381-1390.

Wang Yu, Li Yu, Zhao Quanhua. Integration of multispectral remote-sensing image segmentation with unknown number of classes[J]. Journal of Remote Sensing, 2016, 20(6): 1381-1390. (in Chinese)

[5] 李玉, 徐秋晔, 林文杰, 等. 结合多元信息聚类与空间约束的遥感图像分割方法[J]. 信号处理, 2017, 33(5): 749-757.

Li Yu, Xu Qiuye, Lin Wenjie, et al. Remote sensing image segmentation method combining multivariate information clustering with spatial constraints[J]. Journal of Signal Processing, 2017, 33(5): 749-757. (in Chinese)

[6] Wang X F, Min H, Zou L, et al. A novel level set method for image segmentation by incorporating local statistical analysis and global similarity measurement[J]. Pattern Recognition, 2015, 48(1): 189-204.

[7] 宋熙煜, 周利莉, 李中国, 等. 图像分割中的超像素方法研究综述[J]. 中国图象图形学报, 2015, 20(5): 599- 608.

Song Xiyu, Zhou Lili, Li Zhongguo, et al. Review on superpixel methods in image segmentation[J]. Journal of Image and Graphics, 2015, 20(5): 599- 608. (in Chinese)

[8] Hassner M, Sklansky J. The use of Markov Random Fields as models of texture[J]. Computer Graphics and Image Processing, 1980, 12(4): 357-370.

[9] Besag J. On the Statistical Analysis of Dirty Picture[J]. Journal of the Royal Statistical Society(Series B (Methodological)), 1986, 48(3): 259-302.

[10] 郭雷, 侯一民, 伦向敏. 一种基于图像上下文信息的无监督彩色图像分割算法[J]. 模式识别与人工智能, 2008, 21(1): 82- 87.

Guo Lei, Hou Yimin, Lun Xiangmin. An unsupervised color image segmentation algorithm based on context information[J]. Pattern Recognition and Artificial Intelligence, 2008, 21(1): 82- 87. (in Chinese)

[11] Eggenberger F, Polya G. Uber die statistik verketter vorgange[J]. Zeit Angew Math Mech, 1923, 3(4): 279-289.

[12] 何朝兵. 关于Polya罐子模型的几个结论[J]. 海南大学学报：自然科学版, 2009, 27(4): 332-335.

He Chaobing. Several results of Polya urn model[J]. Natural Science Journal of Hainan University, 2009, 27(4): 332-335. (in Chinese)

[13] Johnson N L, Kotz S. Urn Models and Their Application[M]. New York, United States: John Wiley & Sons, 1977: 176-194.

[14] Alajaji F, Burlina P. Image modeling and restoration through contagion urn schemes[C]∥International Conference on Image Processing. Washington, D.C., United States: IEEE Computer Society Press, 1995, 2: 53-56.

[15] 耿茵茵, 蔡安妮, 孙景鳌. 基于瓦罐模型的多判据判决及其在图像分割中的应用[J]. 电子学报, 2002, 30(7): 1017-1019.

Geng Yinyin, Cai Anni, Sun Jingao. Multiple criterion decisions based on urn model and its application in image segmentation[J]. Acta Electronica Sinica, 2002, 30(7): 1017-1019. (in Chinese)

[16] Banerjee A, Burlina P, Alajaji F. Image segmentation and labeling using the Polya urn model[J]. IEEE Transactions on Image Processing, 1999, 8(9): 1243-1253.

[17] Geman S, Geman D. Stochastic relaxation, Gibbs distribution, and Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6): 721-741.

[18] Chib S, Greenberg E. Understanding the Metropolis-Hastings algorithm[J]. The American Statistician, 1995, 49(4): 327-335.

[19] Zhao Q H, Wang Y, Li Y. Voronoi tessellation-based regionalised segmentation for colour texture image[J]. IET Computer Vision, 2017, 10(7): 613- 622.

[20] Mahmoud M H. Polya Urn Models[M]. Boca Raton, United States: CRC Press, 2009: 50-53.

[21] Spitzer F. Markov Random Fields and Gibbs ensembles[J]. The American Mathematical Monthly, 1971, 78(2): 142-154.

[22] 周辉仁, 郑丕谔, 牛犇, 等. 基于递阶遗传算法和BP网络的模式分类方法[J]. 系统仿真学报, 2009, 21(8): 2243-2247.

Zhou Huiren, Zheng Pie, Niu Ben, et al. HGA-BP-based pattern classification method[J]. Journal of System Simulation, 2009, 21(8): 2243-2247. (in Chinese)

[23] Congaltonr G, Green K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices[M]. Boca Raton, United States: CRC Press, 2008: 105-119.