非平稳信道衰落FPGA实时模拟方法
李 浩 朱秋明,2 陈应兵 陈小敏 杨志强
(1. 南京航空航天大学江苏省物联网与控制技术重点实验室,江苏南京 211100; 2. 英国赫瑞瓦特大学工程与
1 引言
无线信道模拟器可在实验室环境下模拟无线信号的真实传播过程,从而节省大量通信设备测试的时间和成本。目前,国外已有一些商用化信道模拟设备,但是这些设备价格昂贵,且仅适用于特定标准化无线信道测试[1]。
目前,大部分公开报道的信道模型均假设信道衰落满足广义平稳(Wide sense stationary,WSS)条件[2-3]。针对该类平稳信道的实时模拟研究日趋成熟。比如,文献[4]提出的谐波叠加方法(Sum-of-Sinusoids, SoS),在信道仿真中有着广泛的应用;文献[5- 6]进一步对其平稳性和遍历性进行优化,并推广应用至非均匀传播环境。此外,Alimohammad等采用迭代算法完成了SoS方法的FPGA实现,并将其应用于MIMO(Multiple-input Multiple-out,MIMO)信道模拟[7- 8];最近,文献[9]提出了另外一种迭代方案,并对其定点化性能进行了分析;文献[10]指出还可以采用多项式近似逼近余弦函数的方案,从而大大简化硬件实现复杂度。
近年来,大量信道实测结果表明,信道衰落只在短时间内满足WSS条件[11],非平稳衰落特性不可忽视。文献[12]假设散射体固定在随着移动端运动的椭圆上,提出了一种二维非平稳信道模型;文献[13]则针对车间通信场景,假设散射体随着移动端运动,提出了一个三维非平稳信道模型;文献[14]进一步假设移动端随机运动,推导获得了非平稳信道统计特性的理论表达式。需要指出的是,上述文献均采用了传统SoC方法实现非平稳信道衰落的产生。实际中,我们发现该方法产生信道衰落的相位不连续,从而导致多普勒频率与理论值不吻合[15]。
为了解决输出相位连续性问题并实现非平稳信道的高效模拟,本课题组在前期已经做了大量研究,并在文献[16]提出了一种基于多支路线性调频信号叠加(Sum-of-Linear-Frequency-Modulation, SoLFM)思想的非平稳衰落信道的软件仿真方法。基于该思想,本文首先针对时变移动传播场景基站-移动端下行链路,构建相位连续的非平稳衰落信道的理论模型;并据此提出了基于SoLFM的硬件模拟思想及离散域简化产生方法,并详细分析了该方法输出信道衰落的幅值分布和定点化增益等性能指标。最后,利用FPGA硬件平台进行实测验证了该方法的正确性。
2 信道模型
无线电波在传播过程中受到障碍物影响会产生反射、折射和衍射等现象,复基带信道单位冲激响应可建模为
(1)
其中,L表示可分辨簇数目;Cl为确定性路径增益且与传播距离及通信频率有关;μl(t)表示具有相同时延、不同角度的散射支路在接收端叠加后的信道衰落,可进一步表示为(为简化表示以下省略下标l)
(2)
其中,θα,fα分别对应不同支路初始相位及多普勒频率,α,p(α)则分别表示接收信号与移动台移动速度之间的夹角及其分布。
若考虑移动台变速运动或散射体移动因素,无线信道将不满足WSS假设条件,导致信道衰落呈现非平稳特性。目前公开报道的大部分非平稳模型[13-15]将式(2)中的2πfαt简单升级为2πfα(t)t。然而,根据频率和相位之间的对应关系可知,

(3)
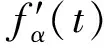
(4)
易证该模型输出信道衰落的时变多普勒频率与理论值一致。
3 非平稳衰落硬件模拟及性能分析
3.1 基于SoLFM的模拟方法
平稳衰落信道常见仿真方法包括滤波法、Markov模型和SoC方法等。其中,SoC方法物理含义明确,易于硬件实现已得到广泛应用,该方法可表示为[17]
(5)
其中,N表示有限条仿真支路数目;θn∈U(0,2π]表示各支路随机初始相位;fn则表示各支路多普勒频率。本文基于该思想,提出的非平稳衰落模拟方法如下,
(6)
进一步假设信道衰落的采样率为fs,式(6)对应的时间离散化模型可表示为
(7)
其中,k表示离散时刻序号;fn[k]表示第k时刻第n仿真支路的多普勒频率。
考虑到实际传播环境下,多普勒频率虽然连续变化,但相对于采样速率而言,变化非常缓慢。为了简化硬件实现复杂度,可以每隔Tu时间间隔(Tu≫1/fs)计算一次。需要指出的是,Tu通常也称为平稳间隔,它表示信道统计特性基本维持不变的最大时间间隔,通常为几至几十毫秒[18]。另外,为了保证Tu时间间隔内多普勒频率仍然连续持续变化,可以合理假设其呈线性变化。因此,多普勒频率参数可以表示为
(8)

(9)
由上式可以看出,该产生方法中各支路信号具有线性调频信号的形式,即利用有限个线性调频信号叠加产生非平稳信道衰落。
3.2 模拟方法性能分析
A) 输出衰落分布
由式(6)可知,第n支路复调频信号的实部可表示为
(10)


(11)
利用特征函数的性质,可得叠加后变量μI(t)的特征函数为
(12)
因此,μI(t)的幅值分布为

(13)
当N→∞时,该式即为高斯分布,同理易证虚部幅值分布也为高斯分布。因此,本文仿真方法输出随机信道衰落与理论值一致且为瑞利分布。
B) 输出衰落增益
为保证最终输出衰落功率增益的归一化,需要预知定点化模型输出衰落的增益。首先,可以证明定点化模型(9)输出随机衰落的理论位宽为
Wid(u)=「log2N⎤+Wcos
(14)
其中,Wcos表示定点化位宽,Wid(·)表示有效位宽;「·⎤表示向上取整。因此,对应输出序列的平均功率可表示为
(15)
将式(15)通过三角函数二倍角和积化和差公式进行展开,
(16)
其中,Pow(·)表示定点化序列的平均功率。式(15)中包含时间变量k的项,平均后均为零。因此,简化式(15)后可得
(17)
同理易证,虚部的平均功率也可以用上式表示,因此输出衰落的总的平均功率可以表示为
Pow(u)=22·(Wcos-1)·N
(18)
3.3 硬件实现及资源消耗

基于SoLFM方法产生非平稳信道衰落是FPGA单元中最关键的模块,也是消耗大部分硬件资源的模块。需要指出的是,式(9)模型中涉及大量支路余弦/正弦函数的计算,由于频率随时间变化,无法采用文献[7]提出的高效迭代或多项式逼近等方法实现,故本文采用查找表的方案进行实时计算。另外,若采用简单并行方案,则系统需要存储2LN个余弦查找表,从而消耗大量存储资源。考虑到信道衰落产生速率远远小于FPGA系统时钟,本文SoLFM模块采用了串行并结合时分复用的思想进行设计,实现框图如图1所示。该方案包括参数存储RAM模块、信道参数更新模块、1/4余弦查找表模块和内插模块。其中,参数存储RAM模块存储CPU单元产生的信道参数,信道参数更新模块实现信道参数的线性内插以及积分计算。其中,1/4余弦查找表通过映射关系可大大降低存储容量,内插模块则将低速率原始信道衰落内插至系统速率。表1比较了散射支路数目为32,位宽分别为16和8的情况下,单个SoLFM模块硬件资源的消耗情况。考虑到FPGA(XC7K325TFFG900-2L)有445个BlockRAM(每一个大小为36 kb),840个DSP和203800个LUT。因此,单片芯片理论上可完成4发4收MIMO信道的实时模拟,故可满足WINNER+[19]和3GPP[3]标准提供的各种场景仿真支路数要求。
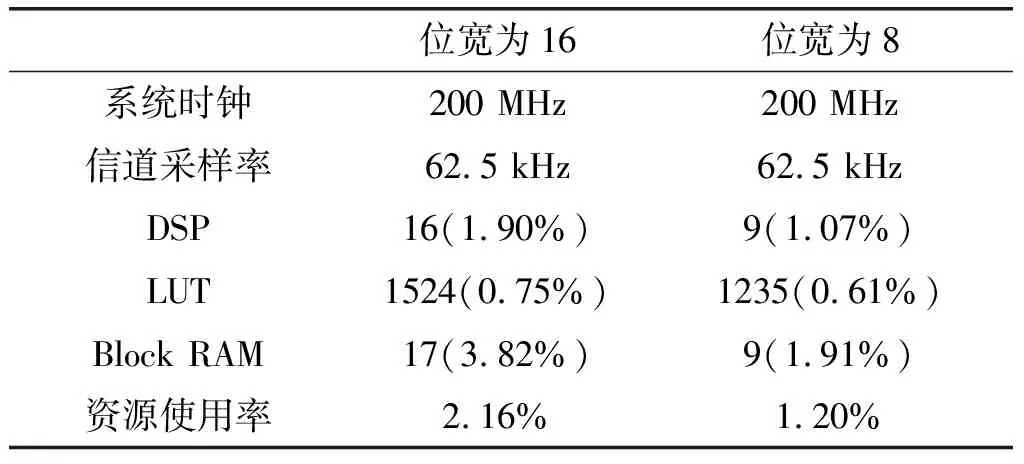
表1 不同位宽SoLFM硬件资源消耗
4 硬件实测结果及分析
为了评估非平稳信道衰落模拟器性能,将对其模拟产生的信道衰落统计特性进行验证。测试参数如下:载波频率2.4 GHz,基站高度200 m,移动台离基站水平距离100 m,并以50 km/h的初速度以及10 km/h的加速度向基站移动,信道衰落速率100 kHz,状态更新间隔20 ms,衰落产生时间10 s。实测中,借助Xilinx公司Vivado开发工具将硬件模拟器输出的信道衰落数据存储并提取,然后利用MATLAB软件对其进行各项统计特性分析。
图2给出了SoC与SoLFM两种模拟方法输出的信道衰落幅值以及相位的对比。由图可以看出SoC方法输出信道衰落的相位存在不连续情况,而本文采用的SoLFM仿真方法通过引入积分运算,不仅对衰落相位进行了平滑,同时也消除了相位突变的情况。需要指出的是,由于二者输出相位的不一致,最终导致输出信道衰落的幅值也不同。
图3(a)给出了不同时刻输出信道衰落幅值的统计分布,由图可以看出不同时刻信道衰落的幅值分布基本不变,原因在于上文分析得出输出信道衰落幅值的统计分布只和仿真支路数目N有关。图3(b)进一步比较了三个时刻t=0 s,t=5 s,t=9 s实测分布与理论分布曲线,由图可以看出两者很吻合,为了定量描述两者的关系,采用Kullback-Leibler(K-L)匹配准则[20],即

图1 SoLFM模块实现框图
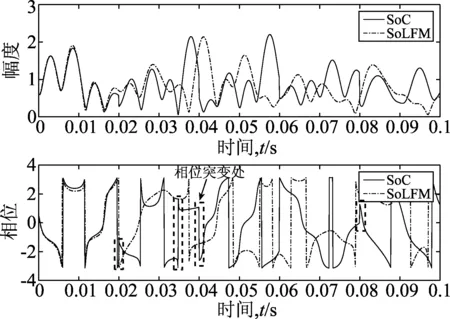
图2 信道衰落幅值及相位实测结果
(19)
其中,p(x),q(x)分别为统计得到的幅值分布和理论的瑞利分布,最终计算出误差D=0.004,可以满足实际中对硬件模拟器输出信道衰落幅值分布的精度要求。
自相关函数在通信系统中具有重要意义,归一化的自相关函数可以表示为
(20)
其中,h(t)为硬件模拟器的信道输出衰落,文献[21]给出了均匀分布情况下的理论自相关函数公式,本文仿真场景下计算出的理论自相关函数如图4(a)所示,很明显由于信道参数的时变导致自相关函数具有时变特性。图4(b)将t=0 s,t=5 s,t=9 s三个时刻的实测自相关函数与理论自相关函数进行了对比,两者非常吻合。
对于非平稳随机过程,多普勒功率谱应采用短时傅里叶变化的形式来描述[22],
(21)
其中,w(t-τ)为分析时间窗函数,在窗函数内可认为信道衰落为平稳的。为了使测试结果更加直观,测试场景修改以下参数,移动台以5 km/h的初速度以及1 km/h的加速度向基站移动,衰落产生时间90 s。文献[21]给出了均匀分布情况下的理论多普勒功率谱计算公式,在本文的仿真场景下计算出的理论多普勒功率谱如图5(a)所示,为了验证硬件模拟器的正确性,使用了Agilent N9340B对硬件模拟器的输出信号的多普勒功率谱进行了测量,图5(b)为仪器测试得到的多普勒功率谱。测试的多普勒功率谱由于随机特性以及定点化的影响,不能与精确计算的理论多普勒功率谱完全一致,只能定性的进行研究[23],可以看出实测结果与仿真值的形状以及变化趋势基本一致。

图3 信道衰落幅值分布实测结果

图4 归一化自相关函数实测结果

图5 时变多普勒功率谱理论和实测结果
上述仿真结果表明,利用本文SoLFM方法仿真输出统计特性与理论值完全吻合,能够有效的复现动态场景下的非平稳衰落信道特性。
5 结论
对于非平稳衰落信道而言,若简单的将其看成分段平稳衰落信道,并采用现有的仿真方法进行产生,无法保证信道状态的连续性。本文提出了一种基于SoLFM的连续非平稳衰落信道的产生方法,该方法结构简单易于FPGA硬件实现。另外,文中还分析了FPGA硬件实现时输出衰落分布和输出增益等指标。硬件实测结果表明SoLFM输出衰落分布于理论值完全吻合,输出的时变多普勒功率谱和时变自相关函数与理论值也非常吻合。
[1] 邵晖. 高性能信道模拟器设计与应用浅析[J]. 国外电子测量技术,2017,36(3):4-9.
Shao Hui. Design and Application of High Performance Channel Simulator[J]. Forrign Electronic Measurement Technology, 2017, 36(3):4-9. (in Chinese)
[2] Series M. ITU-R M.2135-1 Guidelines for Evaluation of Radio Interface Technologies for IMT-Advanced[S]. Switzerland: Report ITU, 2009.
[3] 3GPP TS36.101 V10.2.1 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA); User Equipment (UE) Radio Transmission and Reception(Release 10)[S]. 3GPP TS: 2011.
[4] Jakes W C, Cox D C. Microwave Mobile Communications[M]. Piscataway NJ: Wiley-IEEE Press, 1994.
[5] Pätzold M, Wang C X, Hogstad B O. Two New Sum-of-Sinusoids-Based Methods for the Efficient Generation of Multiple Uncorrelated Rayleigh Fading Waveforms[J]. IEEE Transactions on Wireless Communications, 2009, 8(6):3122-3131.
[6] Gutierrez C A, Pätzold M, Sandoval A, et al. An Ergodic Sum-of-Cisoids Simulator for Multiple Uncorrelated Rayleigh Fading Channels Under Generalized Scattering Conditions[J]. IEEE Transactions on Vehicular Technology, 2012, 61(5):2375-2382.
[7] Alimohammad A, Fard S F, Cockburn B F. Accurate multiple-input multiple-output fading channel simulator using a compact and high throughput reconfigurable architecture[J]. IET Communications, 2011, 5(6): 844- 852.
[8] Alimohammad A, Fard S F. A Compact Architecture for Simulation of Spatio-Temporally Correlated MIMO Fading Channels[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(4): 1280-1288.
[9] Huang P, Du Y, Li Y. Stability Analysis and Hardware Resource Optimization in Channel Emulator Design[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(7): 1089-1100.
[10] Castillo J V, Vela-Garcia L, Gutiérrez C A, et al. A reconfigurable hardware architecture for the simulation of Rayleigh fading channels under arbitrary scattering conditions[J]. AEU-International Journal of Electronics and Communications, 2015, 69(1): 1-13.
[11] Ispas A, Ascheid G, Schneider C, et al. Analysis of local quasi-stationarity regions in an urban macrocell scenario[C]∥Vehicular Technology Conference (VTC 2010-Spring), 2010 IEEE 71st. IEEE, 2010: 1-5.
[12] Ghazal A, Wang C X, Ai B, et al. A nonstationary wideband MIMO channel model for high-mobility intelligent transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 885- 897.
[13] Yuan Y, Wang C X, He Y, et al. 3D wideband non-stationary geometry-based stochastic models for non-isotropic MIMO vehicle-to-vehicle channels[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6883- 6895.
[14] Borhani A, Stüber G L, Pätzold M. A Random Trajectory Approach for the Development of Nonstationary Channel Models Capturing Different Scales of Fading[J]. IEEE Transactions on Vehicular Technology, 2017, 66(1): 2-14.
[15] Dahech W, Pätzold M, Gutierrez C A, et al. A Non-Stationary Mobile-to-Mobile Channel Model Allowing for Velocity and Trajectory Variations of the Mobile Stations[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1987-2000.
[16] Zhu Q, Liu X, Yin X, et al. A Novel Simulator of Nonstationary Random MIMO Channels in Rayleigh Fading Scenarios[J]. International Journal of Antennas and Propagation, 2016,2016(1):9-9.
[17] 朱秋明,戴秀超,刘星麟,等. 复合衰落信道建模及模拟方法研究[J]. 信号处理,2015,31(1):59- 65.
Zhu Qiuming, Dai Xiuchao, Liu Xinglin, et al. A simulation method for fading channel and emulator development[J]. Journal of Signal Processing, 2015, 31(1):59- 65. (in Chinese)
[18] Binghao C, Zhangdui Z, Bo A. Stationarity intervals of time-variant channel in high speed railway scenario[J]. China Communications, 2012, 9(8): 64-70.
[19] Osseiran A, Hardouin E, Boldi M, et al. The Road to IMT-Advanced Communication Systems: State-of-the-Art and Innovation Areas Addressed by the WINNER+Project[J]. IEEE Communications Magazine, 2009, 47(6): 38- 47.
[20] Qi X, Wu N, Wang H, et al. A factor graph-based iterative detection of faster-than-Nyquist signaling in the presence of phase noise and carrier frequency offset[J]. Digital Signal Processing, 2017, 63(1): 25-34.
[21] Pätzold M, Borhani A. A non-stationary multipath fading channel model incorporating the effect of velocity variations of the mobile station[C]∥2014 IEEE Wireless Communications and Networking Conference (WCNC). IEEE, 2014: 182-187.
[22] Stoica P, Moses R L. Spectral Analysis of Signals[M]. Upper Saddle River, NJ: Pearson/Prentice Hall, 2005.
[23] Alimohammad A, Fard S F. FPGA implementation of isotropic and nonisotropic fading channels[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2013, 60(11): 796- 800.

